Οι μηχανικοί αντιμετωπίζουν σύγχυση κατά τον υπολογισμό των όγκων για πεπλατυσμένα σφαιρικά εξαρτήματα σε συστήματα πνευματικών κυλίνδρων χωρίς ράβδο. Οι λανθασμένοι υπολογισμοί όγκου οδηγούν σε λανθασμένους υπολογισμούς πίεσης και αστοχίες του συστήματος.
Μια επίπεδη σφαίρα (πεπλατυσμένο σφαιροειδές) έχει όγκο V = (4/3)πa²b, όπου "a" είναι η ισημερινή ακτίνα και "b" είναι η πολική ακτίνα, που συνήθως συναντάται σε πνευματικός συσσωρευτής1 και εφαρμογές απορρόφησης.
Τον περασμένο μήνα, βοήθησα τον Andreas, έναν μηχανικό σχεδιασμού από τη Γερμανία, του οποίου το πνευματικό σύστημα απορρόφησης απέτυχε επειδή χρησιμοποίησε υπολογισμούς τυπικού όγκου σφαίρας αντί για υπολογισμούς επίπεδου σφαιροειδούς για τους πεπλατυσμένους θαλάμους του συσσωρευτή.
Πίνακας περιεχομένων
- Τι είναι η επίπεδη σφαίρα στις πνευματικές εφαρμογές;
- Πώς υπολογίζετε τον όγκο επίπεδης σφαίρας;
- Πού χρησιμοποιούνται οι επίπεδες σφαίρες σε κυλίνδρους χωρίς ράβδο;
- Πώς επηρεάζει η ισοπέδωση τον όγκο και την απόδοση;
Τι είναι η επίπεδη σφαίρα στις πνευματικές εφαρμογές;
Μια επίπεδη σφαίρα, που τεχνικά ονομάζεται πεπλατυσμένο σφαιροειδές2, είναι ένα τρισδιάστατο σχήμα που δημιουργείται όταν μια σφαίρα συμπιέζεται κατά μήκος ενός άξονα και χρησιμοποιείται συνήθως σε σχέδια πνευματικών συσσωρευτών και μαξιλαριών.
Μια επίπεδη σφαίρα προκύπτει από την ισοπέδωση μιας τέλειας σφαίρας κατά μήκος του κατακόρυφου άξονά της, δημιουργώντας μια ελλειπτική διατομή με διαφορετικές οριζόντιες και κατακόρυφες ακτίνες.
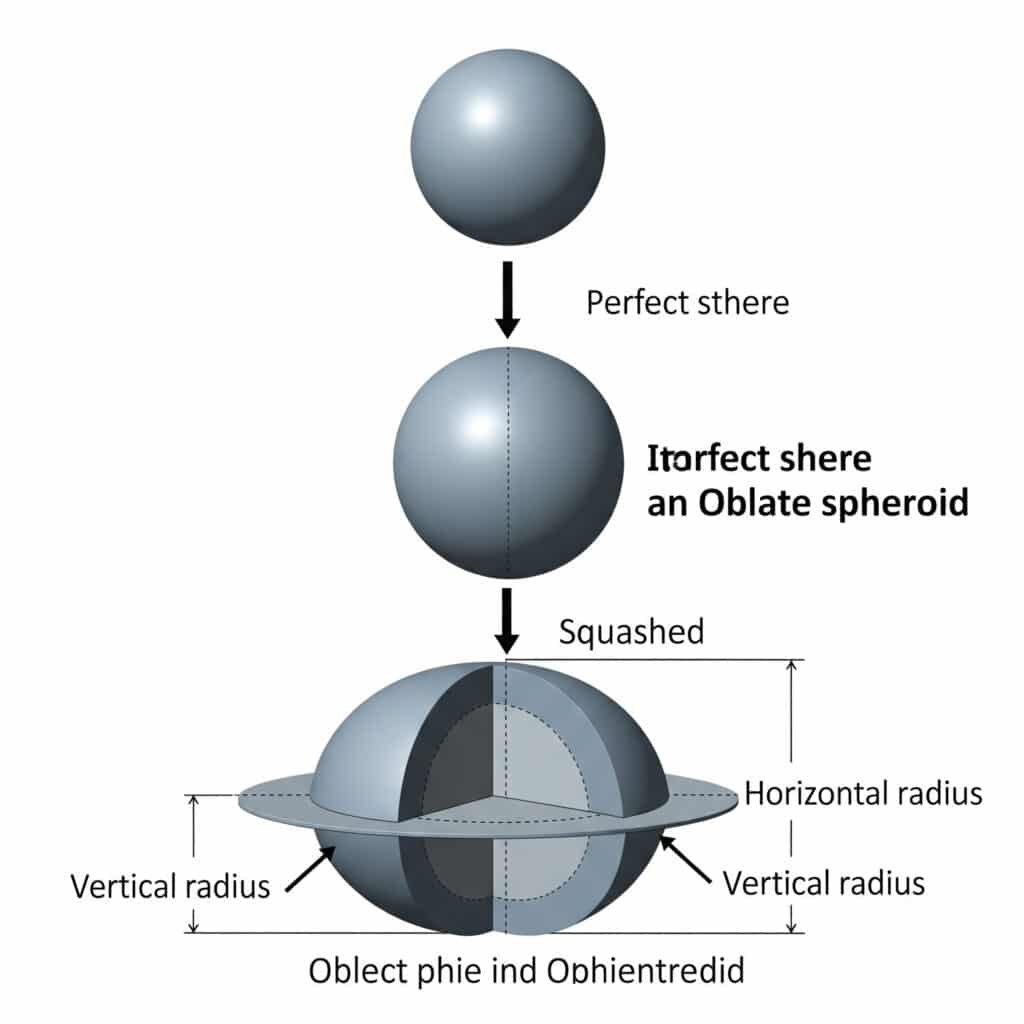
Γεωμετρικός ορισμός
Χαρακτηριστικά σχήματος
- Οβελιαίο σφαιροειδές: Τεχνικός γεωμετρικός όρος
- Πεπλατυσμένη σφαίρα: Κοινή βιομηχανική περιγραφή
- Ελλειπτικό προφίλ: Διατομή
- Περιστροφική συμμετρία: Γύρω από τον κατακόρυφο άξονα
Βασικές διαστάσεις
- Ισημερινή ακτίνα (α): Οριζόντια ακτίνα (μεγαλύτερη)
- Πολική ακτίνα (b): Κατακόρυφη ακτίνα (μικρότερη)
- Λόγος ισοπέδωσης: b/a < 1,0
- Αναλογία διαστάσεων: Σχέση ύψους προς πλάτος
Επίπεδη σφαίρα vs Τέλεια σφαίρα
| Χαρακτηριστικό | Τέλεια σφαίρα | Επίπεδη σφαίρα |
|---|---|---|
| Σχήμα | Ομοιόμορφη ακτίνα | Συμπιεσμένο κάθετα |
| Τύπος όγκου | (4/3)πr³ | (4/3)πa²b |
| Διατομή | Κύκλος | Έλλειψη |
| Συμμετρία | Όλες οι κατευθύνσεις | Μόνο οριζόντια |
Κοινές αναλογίες ισοπέδωσης
Επιπεδοποίηση φωτός
- Αναλογία: b/a = 0,8-0,9
- Εφαρμογές: Μικροί περιορισμοί χώρου
- Επιπτώσεις στον όγκο: 10-20% μείωση
- Επιδόσεις: Ελάχιστο αποτέλεσμα
Μέτρια ισοπέδωση
- Αναλογία: b/a = 0,6-0,8
- Εφαρμογές: Τυποποιημένα σχέδια συσσωρευτών
- Επιπτώσεις στον όγκο: 20-40% μείωση
- Επιδόσεις: Αισθητές αλλαγές πίεσης
Βαριά ισοπέδωση
- Αναλογία: b/a = 0,3-0,6
- Εφαρμογές: Σοβαροί περιορισμοί χώρου
- Επιπτώσεις στον όγκο: 40-70% μείωση
- Επιδόσεις: Σημαντικά ζητήματα σχεδιασμού
Πνευματικές εφαρμογές
Θάλαμοι συσσωρευτών
Συναντώ επίπεδες σφαίρες σε:
- Εγκαταστάσεις περιορισμένου χώρου: Περιορισμοί ύψους
- Ολοκληρωμένα σχέδια: Ενσωματωμένο σε πλαίσια μηχανημάτων
- Προσαρμοσμένες εφαρμογές: Ειδικές απαιτήσεις όγκου
- Έργα αναβάθμισης: Εγκατάσταση σε υπάρχοντες χώρους
Συστήματα απορρόφησης
- Απόσβεση στο τέλος της διαδρομής: Εφαρμογές κυλίνδρων χωρίς ράβδο
- Απορρόφηση κραδασμών: Διαχείριση φορτίου επιπτώσεων
- Ρύθμιση πίεσης: Έλεγχος ομαλής λειτουργίας
- Μείωση θορύβου: Αθόρυβη λειτουργία του συστήματος
Σκέψεις σχετικά με την κατασκευή
Μέθοδοι παραγωγής
- Βαθύ σχέδιο: Διαμόρφωση λαμαρίνας
- Hydroforming: Διαδικασία διαμόρφωσης ακριβείας
- Κατεργασία: Προσαρμοσμένα μεμονωμένα εξαρτήματα
- Casting: Παραγωγή μεγάλου όγκου
Επιλογή υλικού
- Χάλυβας: Εφαρμογές υψηλής πίεσης
- Αλουμίνιο: Σχέδια ευαίσθητα στο βάρος
- Ανοξείδωτο ατσάλι: Διαβρωτικά περιβάλλοντα
- Σύνθετα υλικά: Εξειδικευμένες απαιτήσεις
Πώς υπολογίζετε τον όγκο επίπεδης σφαίρας;
Ο υπολογισμός του όγκου επίπεδης σφαίρας απαιτεί τον τύπο του πλατύ σφαιροειδούς χρησιμοποιώντας μετρήσεις τόσο της ισημερινής όσο και της πολικής ακτίνας για τον ακριβή σχεδιασμό του πνευματικού συστήματος.
Χρησιμοποιήστε τον τύπο V = (4/3)πa²b όπου "a" είναι η ισημερινή ακτίνα (οριζόντια) και "b" είναι η πολική ακτίνα (κατακόρυφη) για να υπολογίσετε με ακρίβεια τον όγκο της επίπεδης σφαίρας.
Κατανομή τύπου όγκου
Τυποποιημένη φόρμουλα
V = (4/3)πa²b
- V: Όγκος σε κυβικές μονάδες
- π: 3.14159 (μαθηματική σταθερά)
- a: Ισημερινή ακτίνα (οριζόντια)
- b: Πολική ακτίνα (κατακόρυφη)
- 4/3: Συντελεστής όγκου σφαιροειδούς
Συνιστώσες της φόρμουλας
- Ισημερινή περιοχή: πa² (οριζόντια διατομή)
- Πολική κλιμάκωση: συντελεστής b (κατακόρυφη συμπίεση)
- Συντελεστής όγκου: 4/3 (γεωμετρική σταθερά)
- Μονάδες αποτελέσματος: Μονάδες ακτίνας εισόδου σε κύβους
Υπολογισμός βήμα προς βήμα
Διαδικασία μέτρησης
- Μέτρηση της ισημερινής διαμέτρου: Ευρύτερη οριζόντια διάσταση
- Υπολογισμός της ισημερινής ακτίναςα = διάμετρος ÷ 2
- Μέτρηση πολικής διαμέτρου: Κατακόρυφη διάσταση ύψους
- Υπολογισμός πολικής ακτίνας: b = ύψος ÷ 2
- Εφαρμόστε τη φόρμουλα: V = (4/3)πa²b
Παράδειγμα υπολογισμού
Για πνευματικό συσσωρευτή:
- Ισημερινή διάμετρος: 100mm → a = 50mm
- Πολική διάμετρος: 60mm → b = 30mm
- Τόμος: V = (4/3)π(50)²(30)
- Αποτέλεσμα: V = (4/3)π(2500)(30) = 314,159 mm³
Παραδείγματα υπολογισμού όγκου
| Ισημερινή ακτίνα | Πολική ακτίνα | Λόγος ισοπέδωσης | Τόμος | Σύγκριση με το Sphere |
|---|---|---|---|---|
| 50mm | 50mm | 1.0 | 523,599 mm³ | 100% (τέλεια σφαίρα) |
| 50mm | 40mm | 0.8 | 418,879 mm³ | 80% |
| 50mm | 30mm | 0.6 | 314,159 mm³ | 60% |
| 50mm | 20mm | 0.4 | 209.440 mm³ | 40% |
Εργαλεία υπολογισμού
Χειροκίνητος υπολογισμός
- Επιστημονική αριθμομηχανή: Με τη συνάρτηση π
- Επαλήθευση τύπου: Διπλός έλεγχος των εισόδων
- Συνέπεια μονάδας: Διατηρήστε τις ίδιες μονάδες σε όλη τη διάρκεια
- Ακρίβεια: Υπολογίστε με τα κατάλληλα δεκαδικά ψηφία
Ψηφιακά εργαλεία
- Λογισμικό μηχανικής: Υπολογισμοί όγκου CAD
- Υπολογιστές σε απευθείας σύνδεση: Εργαλεία επίπεδου σφαιροειδούς
- Τύποι υπολογιστικών φύλλων: Αυτοματοποιημένοι υπολογισμοί
- Εφαρμογές για κινητά: Εργαλεία υπολογισμού πεδίου
Συνήθη σφάλματα υπολογισμού
Λάθη μέτρησης
- Ακτίνα έναντι διαμέτρου: Χρήση λανθασμένης διάστασης
- Σύγχυση των αξόνων: Ανάμειξη οριζόντιων/κάθετων μετρήσεων
- Ασυνέπεια μονάδας: ανάμιξη mm vs ίντσες
- Απώλεια ακρίβειας: Στρογγυλοποίηση πολύ νωρίς
Σφάλματα τύπου
- Λάθος τύπος: Χρήση σφαίρας αντί σφαιροειδούς
- Αντιστροφή παραμέτρων: Ανταλλαγή τιμών a και b
- Λάθη συντελεστή: Λείπει ο παράγοντας 4/3
- π προσέγγιση: Χρήση της έκδοσης 3.14 αντί της 3.14159
Μέθοδοι επαλήθευσης
Τεχνικές διασταύρωσης
- Λογισμικό CAD: Υπολογισμός όγκου 3D μοντέλου
- Μετατόπιση νερού: Φυσική μέτρηση όγκου
- Πολλαπλοί υπολογισμοί: Σύγκριση διαφορετικών μεθόδων
- Προδιαγραφές κατασκευαστή: Δημοσιευμένα στοιχεία όγκου
Έλεγχοι λογικότητας
- Μείωση όγκου: Θα πρέπει να είναι λιγότερο από τέλεια σφαίρα
- Ισοπέδωση της συσχέτισης: Περισσότερη ισοπέδωση = λιγότερος όγκος
- Επαλήθευση μονάδας: Τα αποτελέσματα αντιστοιχούν στο αναμενόμενο μέγεθος
- Καταλληλότητα εφαρμογής: Ο τόμος πληροί τις απαιτήσεις του συστήματος
Όταν βοήθησα τη Μαρία, μια σχεδιάστρια πνευματικών συστημάτων από την Ισπανία, να υπολογίσει τους όγκους των συσσωρευτών για την εγκατάσταση του κυλίνδρου χωρίς ράβδο, ανακαλύψαμε ότι οι αρχικοί της υπολογισμοί χρησιμοποιούσαν τύπους σφαίρας αντί για πλατύ σφαιροειδές, με αποτέλεσμα την υπερεκτίμηση του όγκου 35% και την ανεπαρκή απόδοση του συστήματος.
Πού χρησιμοποιούνται οι επίπεδες σφαίρες σε κυλίνδρους χωρίς ράβδο;
Οι επίπεδες σφαίρες εμφανίζονται σε διάφορα εξαρτήματα πνευματικών κυλίνδρων χωρίς ράβδο, όπου οι περιορισμοί χώρου απαιτούν βελτιστοποίηση του όγκου, διατηρώντας παράλληλα τη λειτουργικότητα του δοχείου πίεσης.
Οι επίπεδες σφαίρες χρησιμοποιούνται συνήθως σε θαλάμους συσσωρευτών, συστήματα απορρόφησης και ενσωματωμένα δοχεία πίεσης σε συγκροτήματα κυλίνδρων χωρίς ράβδο, όπου οι περιορισμοί ύψους περιορίζουν τους τυπικούς σφαιρικούς σχεδιασμούς.
Εφαρμογές συσσωρευτών
Ενσωματωμένοι συσσωρευτές
- Βελτιστοποίηση χώρου: Ταιριάζει στα πλαίσια των μηχανημάτων
- Αποδοτικότητα όγκου: Μέγιστη αποθήκευση σε περιορισμένο ύψος
- Σταθερότητα πίεσης: Ομαλή λειτουργία κατά τη διάρκεια των αιχμών ζήτησης
- Ενσωμάτωση συστήματος: Ενσωματωμένο στις βάσεις τοποθέτησης κυλίνδρων
Εγκαταστάσεις αναβάθμισης
- Υφιστάμενα μηχανήματα: Περιορισμοί απόστασης ύψους
- Έργα αναβάθμισης: Προσθήκη συσσώρευσης σε παλαιότερα συστήματα
- Περιορισμοί χώρου: Εργασία εντός του αρχικού φακέλου σχεδιασμού
- Βελτίωση των επιδόσεων: Ενισχυμένη απόκριση του συστήματος
Συστήματα απορρόφησης
Απόσβεση στο τέλος του κτυπήματος
Εγκαθιστώ επίπεδη σφαίρα για:
- Μαγνητικοί κύλινδροι χωρίς ράβδο: Ομαλή επιβράδυνση
- Καθοδηγούμενοι κύλινδροι χωρίς ράβδο: Μείωση των επιπτώσεων
- Κύλινδροι διπλής ενέργειας χωρίς ράβδο: Αμφίδρομη αντικραδασμική προστασία
- Εφαρμογές υψηλών ταχυτήτων: Απορρόφηση κραδασμών
Ρύθμιση πίεσης
- Εξομάλυνση ροής: Εξάλειψη των αιχμών πίεσης
- Μείωση θορύβου: Αθόρυβη λειτουργία
- Προστασία εξαρτημάτων: Μειωμένη φθορά και καταπόνηση
- Σταθερότητα του συστήματος: Σταθερή απόδοση
Εξειδικευμένα εξαρτήματα
Σκάφη πίεσης
- Προσαρμοσμένες εφαρμογές: Μοναδικές απαιτήσεις χώρου
- Σχέδια πολλαπλών λειτουργιών: Συνδυασμένη αποθήκευση και τοποθέτηση
- Αρθρωτά συστήματα: Στοιβαζόμενες διαμορφώσεις
- Πρόσβαση στη συντήρηση: Χρησιμοποίητα σχέδια
Θάλαμοι αισθητήρων
- Παρακολούθηση πίεσης: Ολοκληρωμένα συστήματα μέτρησης
- Ανίχνευση ροής: Εφαρμογές ανίχνευσης ταχύτητας
- Διαγνωστικά συστήματος: Παρακολούθηση επιδόσεων
- Συστήματα ασφαλείας: Ενσωμάτωση ανακούφισης πίεσης
Σκέψεις σχεδιασμού
Περιορισμοί χώρου
| Εφαρμογή | Όριο ύψους | Τυπική ισοπέδωση | Αντίκτυπος όγκου |
|---|---|---|---|
| Τοποθέτηση κάτω από το δάπεδο | 50mm | b/a = 0,3 | Μείωση 70% |
| Ενσωμάτωση μηχανών | 100mm | b/a = 0,6 | Μείωση 40% |
| Εφαρμογές εκ των υστέρων | 150mm | b/a = 0,8 | Μείωση 20% |
| Τυπική τοποθέτηση | 200mm+ | b/a = 0,9 | Μείωση 10% |
Απαιτήσεις επιδόσεων
- Ονομαστική πίεση: Διατήρηση της δομικής ακεραιότητας
- Χωρητικότητα όγκου: Καλύψτε τη ζήτηση του συστήματος
- Χαρακτηριστικά ροής: Επαρκής διαστασιολόγηση εισόδου/εξόδου
- Πρόσβαση στη συντήρηση: Σκέψεις σχετικά με τη λειτουργικότητα
Παραδείγματα εγκατάστασης
Μηχανήματα συσκευασίας
- Εφαρμογή: Εξοπλισμός πλήρωσης υψηλής ταχύτητας
- Περιορισμός: 40mm απόσταση ύψους
- Λύση: Ισχυρά πεπλατυσμένος συσσωρευτής (b/a = 0,25)
- Αποτέλεσμα: 75% μείωση του όγκου, επαρκής απόδοση
Συναρμολόγηση αυτοκινήτων
- Εφαρμογή: Ρομποτικό σύστημα εντοπισμού θέσης
- Περιορισμός: Ενσωμάτωση στη βάση ρομπότ
- Λύση: Μέτρια ισοπέδωση (b/a = 0,7)
- Αποτέλεσμα: 30% εξοικονόμηση χώρου, διατήρηση της απόδοσης
Επεξεργασία τροφίμων
- Εφαρμογή: Σύστημα κυλίνδρου χωρίς ράβδο υγιεινής
- Περιορισμός: Εκκαθάριση περιβάλλοντος πλύσης
- Λύση: Προσαρμοσμένο σχέδιο επίπεδης σφαίρας
- Αποτέλεσμα: Βαθμολογία IP69K3 με βελτιστοποιημένο όγκο
Προδιαγραφές κατασκευής
Τυποποιημένα μεγέθη
- Μικρό: 50mm ισημερινός, διάφορες πολικές διαστάσεις
- Μεσαίο: 100mm ισημερινός, διακυμάνσεις ύψους
- Μεγάλο: Ισημερινός 200mm, προσαρμοσμένο πολικό μέγεθος
- Προσαρμοσμένο: Διαστάσεις για συγκεκριμένη εφαρμογή
Επιλογές υλικού
- Χάλυβας άνθρακα: Τυπικές εφαρμογές πίεσης
- Ανοξείδωτο ατσάλι: Διαβρωτικά περιβάλλοντα
- Αλουμίνιο: Εγκαταστάσεις ευαίσθητες στο βάρος
- Σύνθετο: Εξειδικευμένες απαιτήσεις
Πέρυσι, συνεργάστηκα με τον Thomas, έναν κατασκευαστή μηχανών από την Ελβετία, ο οποίος χρειαζόταν αποθήκευση συσσωρευτών για τη συμπαγή γραμμή συσκευασίας του. Οι τυποποιημένοι σφαιρικοί συσσωρευτές δεν θα χωρούσαν στον περιορισμό ύψους 60 mm, οπότε σχεδιάσαμε επίπεδους σφαιρικούς συσσωρευτές με λόγο b/a = 0,4, επιτυγχάνοντας 60% του αρχικού όγκου, ενώ πληρούσαμε όλους τους περιορισμούς χώρου.
Πώς επηρεάζει η ισοπέδωση τον όγκο και την απόδοση;
Η επιπλάτυνση μειώνει σημαντικά τη χωρητικότητα όγκου, ενώ επηρεάζει τη δυναμική της πίεσης, τα χαρακτηριστικά ροής και τη συνολική απόδοση του συστήματος σε εφαρμογές πεπιεσμένου αέρα χωρίς ράβδους.
Κάθε αύξηση κατά 10% στην επιπεδότητα (μείωση του λόγου b/a) μειώνει τον όγκο κατά περίπου 10% και επηρεάζει την απόκριση πίεσης, τα μοτίβα ροής και την απόδοση του συστήματος σε εφαρμογές πνευματικών συσσωρευτών.
Ανάλυση επιπτώσεων σε όγκο
Σχέσεις μείωσης όγκου
Λόγος όγκου = (β/α) για πλατύσχημα σφαιροειδή
- Γραμμική σχέση: Ο όγκος μειώνεται αναλογικά με την επιπέδωση
- Προβλέψιμος αντίκτυπος: Εύκολος υπολογισμός αλλαγών όγκου
- Ευελιξία σχεδιασμού: Επιλέξτε τη βέλτιστη αναλογία ισοπέδωσης
- Συμβιβασμοί επιδόσεων: Ισορροπία χώρου και χωρητικότητας
Ποσοτικοποιημένες αλλαγές όγκου
| Λόγος εξομάλυνσης (β/α) | Διατήρηση όγκου | Απώλεια όγκου | Καταλληλότητα εφαρμογής |
|---|---|---|---|
| 0.9 | 90% | 10% | Εξαιρετικό |
| 0.8 | 80% | 20% | Πολύ καλά |
| 0.7 | 70% | 30% | Καλή |
| 0.6 | 60% | 40% | Δίκαιη |
| 0.5 | 50% | 50% | Φτωχό |
| 0.4 | 40% | 60% | Πολύ κακή |
Επιπτώσεις απόδοσης πίεσης
Χαρακτηριστικά απόκρισης πίεσης
- Μειωμένος όγκος: Ταχύτερες αλλαγές πίεσης
- Υψηλότερη ευαισθησία: Ανταποκρίνεται καλύτερα στις μεταβολές της ροής
- Αυξημένη ποδηλασία: Συχνότεροι κύκλοι φόρτισης/εκφόρτισης
- Αστάθεια του συστήματος: Πιθανές ταλαντώσεις πίεσης
Ρυθμίσεις υπολογισμού πίεσης
P₁V₁ = P₂V₂ (Νόμος του Boyle4 ισχύει)
- Μικρότερος όγκος: Υψηλότερη πίεση για την ίδια μάζα αέρα
- Ταλαντεύσεις πίεσης: Μεγαλύτερες διακυμάνσεις κατά τη λειτουργία
- Διαστασιολόγηση συστήματος: Αντισταθμίστε με μεγαλύτερη χωρητικότητα συμπιεστή
- Περιθώρια ασφαλείας: Αυξημένες απαιτήσεις ονομαστικής πίεσης
Χαρακτηριστικά ροής
Αλλαγές στο μοτίβο ροής
- Αύξηση της τύρβης: Το πεπλατυσμένο σχήμα δημιουργεί διαταραχές ροής
- Πτώση πίεσης: Υψηλότερη αντίσταση μέσω παραμορφωμένων θαλάμων
- Επιδράσεις εισόδου/εξόδου: Η τοποθέτηση του λιμανιού γίνεται κρίσιμη
- Ταχύτητα ροής: Αυξημένες ταχύτητες σε απαγορευμένα τμήματα
Επίπτωση ρυθμού ροής
- Μειωμένη ωφέλιμη περιοχή: Αναπτύσσονται περιορισμοί ροής
- Απώλειες πίεσης: Η ενεργειακή απόδοση μειώνεται
- Χρόνος απόκρισης: Χαμηλότεροι ρυθμοί πλήρωσης/εκφόρτισης
- Απόδοση συστήματος: Συνολική μείωση της απόδοσης
Δομικές εκτιμήσεις
Κατανομή τάσεων
- Συγκεντρωμένες πιέσεις: Υψηλότερα φορτία στις πεπλατυσμένες περιοχές
- Πάχος υλικού: Μπορεί να χρειαστεί ενίσχυση
- Αντοχή στην κόπωση5: Μειωμένο δυναμικό κύκλου ζωής
- Παράγοντες ασφαλείας: Απαιτούνται αυξημένα περιθώρια σχεδιασμού
Επίδραση βαθμολογίας πίεσης
| Λόγος ισοπέδωσης | Αύξηση του στρες | Συνιστώμενος συντελεστής ασφαλείας | Πάχος υλικού |
|---|---|---|---|
| 0.9 | 10% | 1.5 | Πρότυπο |
| 0.8 | 25% | 1.8 | +10% |
| 0.7 | 45% | 2.0 | +20% |
| 0.6 | 70% | 2.5 | +35% |
Βελτιστοποίηση απόδοσης συστήματος
Στρατηγικές αποζημίωσης
- Αυξημένη ποσότητα συσσωρευτή: Πολλαπλές μικρότερες μονάδες
- Λειτουργία υψηλότερης πίεσης: Αντιστάθμιση της απώλειας όγκου
- Βελτιωμένος σχεδιασμός ροής: Βελτιστοποίηση των διαμορφώσεων εισόδου/εξόδου
- Ρύθμιση συστήματος: Ρύθμιση παραμέτρων ελέγχου
Παρακολούθηση επιδόσεων
- Συχνότητα κύκλων πίεσης: Παρακολούθηση της σταθερότητας του συστήματος
- Μετρήσεις ρυθμού ροής: Επαλήθευση επαρκούς χωρητικότητας
- Επιδράσεις της θερμοκρασίας: Ελέγξτε για υπερβολική θέρμανση
- Διαστήματα συντήρησης: Προσαρμογή με βάση την απόδοση
Οδηγίες σχεδιασμού
Βέλτιστη επιλογή επιπέδωσης
- b/a > 0,8: Ελάχιστες επιπτώσεις στην απόδοση
- b/a = 0,6-0,8: Αποδεκτό για τις περισσότερες εφαρμογές
- b/a = 0,4-0,6: Απαιτεί προσεκτικό σχεδιασμό του συστήματος
- b/a < 0,4: Γενικά δεν συνιστάται
Συστάσεις για συγκεκριμένες εφαρμογές
- Ποδηλασία υψηλής συχνότητας: Ελαχιστοποίηση της ισοπέδωσης (b/a > 0,7)
- Εγκαταστάσεις κρίσιμης σημασίας για το διάστημα: Αποδοχή συμβιβασμών απόδοσης
- Κρίσιμα για την ασφάλεια συστήματα: Συντηρητικές αναλογίες εξομάλυνσης
- Έργα ευαίσθητα στο κόστος: Ισορροπία επιδόσεων έναντι εξοικονόμησης χώρου
Δεδομένα επιδόσεων σε πραγματικό κόσμο
Αποτελέσματα μελέτης περίπτωσης
Όταν ανέλυσα δεδομένα απόδοσης από 50 εγκαταστάσεις με διάφορες αναλογίες ισοπέδωσης:
- 10% ισοπέδωση: Αμελητέος αντίκτυπος στις επιδόσεις
- Ισοπέδωση 30%: 15% αύξηση της συχνότητας ποδηλασίας
- 50% ισοπέδωση: 40% μείωση της πραγματικής χωρητικότητας
- 70% ισοπέδωση: Αστάθεια του συστήματος σε 60% των περιπτώσεων
Επιτυχία βελτιστοποίησης
Για την Elena, έναν ολοκληρωτή συστήματος από την Ιταλία, βελτιστοποιήσαμε τον σχεδιασμό του συσσωρευτή κυλίνδρου χωρίς ράβδο περιορίζοντας την επιπεδοποίηση σε b/a = 0,75, επιτυγχάνοντας εξοικονόμηση χώρου 25%, διατηρώντας παράλληλα 95% της αρχικής απόδοσης του συστήματος και εξαλείφοντας τα προβλήματα αστάθειας της πίεσης.
Συμπέρασμα
Ο όγκος της επίπεδης σφαίρας χρησιμοποιεί τον τύπο V = (4/3)πa²b με ισημερινή ακτίνα "a" και πολική ακτίνα "b". Η επιπλάτυνση μειώνει αναλογικά τον όγκο, αλλά επηρεάζει την απόκριση πίεσης και τα χαρακτηριστικά ροής σε πνευματικές εφαρμογές.
Συχνές ερωτήσεις σχετικά με τον όγκο επίπεδης σφαίρας
Ποιος είναι ο τύπος για τον όγκο της επίπεδης σφαίρας;
Ο τύπος του όγκου της επίπεδης σφαίρας (πλατύ σφαιροειδές) είναι V = (4/3)πa²b, όπου "a" είναι η ισημερινή ακτίνα (οριζόντια) και "b" είναι η πολική ακτίνα (κατακόρυφη). Αυτό διαφέρει από τον τύπο της τέλειας σφαίρας V = (4/3)πr³.
Πόσος όγκος χάνεται κατά την ισοπέδωση μιας σφαίρας;
Η απώλεια όγκου ισούται με τον λόγο ισοπέδωσης. Εάν η πολική ακτίνα είναι 70% της ισημερινής ακτίνας (b/a = 0,7), ο όγκος γίνεται 70% του αρχικού όγκου της σφαίρας, που αντιστοιχεί σε μείωση του όγκου κατά 30%.
Πού χρησιμοποιούνται επίπεδες σφαίρες σε πνευματικά συστήματα;
Οι επίπεδες σφαίρες χρησιμοποιούνται σε θαλάμους συσσωρευτών, συστήματα απορρόφησης και δοχεία πίεσης, όπου οι περιορισμοί ύψους περιορίζουν τους τυπικούς σφαιρικούς σχεδιασμούς. Οι συνήθεις εφαρμογές περιλαμβάνουν την ενσωμάτωση μηχανημάτων με περιορισμένο χώρο και εγκαταστάσεις μετασκευής.
Πώς επηρεάζει η ισοπέδωση την απόδοση του πεπιεσμένου αέρα;
Η επιπλάτυνση μειώνει τη χωρητικότητα όγκου, αυξάνει την ευαισθησία στην πίεση και δημιουργεί αναταράξεις στη ροή. Συστήματα με συσσωρευτές με έντονη επιπεδοποίηση (b/a < 0,6) ενδέχεται να παρουσιάσουν αστάθεια πίεσης και μειωμένη απόδοση που απαιτούν αντιστάθμιση σχεδιασμού.
Ποια είναι η μέγιστη συνιστώμενη αναλογία ισοπέδωσης;
Για πνευματικές εφαρμογές, διατηρήστε αναλογίες ισοπέδωσης πάνω από b/a = 0,6 για αποδεκτή απόδοση. Λόγοι κάτω από 0,4 προκαλούν γενικά αστάθεια του συστήματος και απαιτούν σημαντικές τροποποιήσεις στο σχεδιασμό για τη διατήρηση της επαρκούς λειτουργίας.
-
Κατανόηση της λειτουργίας και του σκοπού των πνευματικών συσσωρευτών στα συστήματα ισχύος ρευστών. ↩
-
Μάθετε τον μαθηματικό ορισμό και τις γεωμετρικές ιδιότητες του πλατύ σφαιροειδούς. ↩
-
Ανατρέξτε στον επίσημο ορισμό και τις απαιτήσεις δοκιμών για την κατηγορία προστασίας από εισχώρηση IP69K. ↩
-
Επανεξετάστε τις αρχές του νόμου του Boyle, ο οποίος περιγράφει τη σχέση μεταξύ πίεσης και όγκου σε ένα αέριο. ↩
-
Εξερευνήστε την έννοια της αντοχής στην κόπωση και τον τρόπο με τον οποίο τα υλικά συμπεριφέρονται υπό κυκλική φόρτιση. ↩




