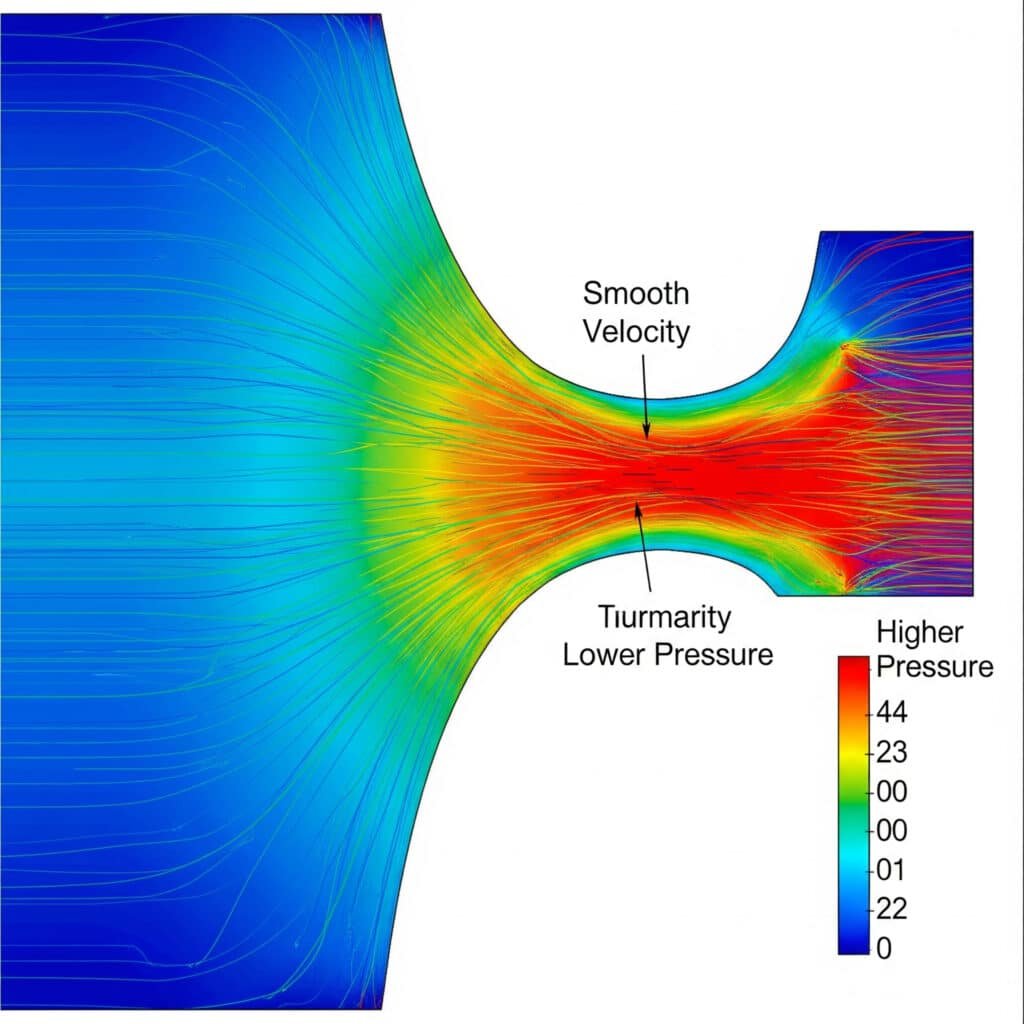
Τα προβλήματα ροής αερίου κοστίζουν στους κατασκευαστές δισεκατομμύρια ετησίως σε σπατάλη ενέργειας και βλάβες του συστήματος. Οι μηχανικοί συχνά εφαρμόζουν τις αρχές ροής υγρών σε συστήματα αερίου, οδηγώντας σε καταστροφικούς λανθασμένους υπολογισμούς. Η κατανόηση των αρχών ροής αερίου αποτρέπει τα δαπανηρά σφάλματα σχεδιασμού και τους κινδύνους για την ασφάλεια.
Η αρχή της ροής αερίου διέπεται από την εξίσωση συνέχειας, τη διατήρηση της ορμής και τη διατήρηση της ενέργειας, όπου η ταχύτητα, η πίεση, η πυκνότητα και η θερμοκρασία του αερίου αλληλεπιδρούν μέσω συμπιεστή ροή1 εξισώσεις θεμελιωδώς διαφορετικές από την ασυμπίεστη ροή υγρών.
Πριν από δύο χρόνια, συνεργάστηκα με μια Βρετανίδα χημικό μηχανικό, τη Σάρα Τόμσον, το σύστημα διανομής φυσικού αερίου της οποίας παρουσίαζε επικίνδυνες διακυμάνσεις πίεσης. Η ομάδα της χρησιμοποιούσε υπολογισμούς ασυμπίεστης ροής για συμπιεστή ροή αερίου. Αφού εφαρμόσαμε τις σωστές αρχές ροής αερίου, εξαλείψαμε τις αυξομειώσεις πίεσης και μειώσαμε την κατανάλωση ενέργειας κατά 35%.
Πίνακας περιεχομένων
- Ποιες είναι οι θεμελιώδεις αρχές που διέπουν τη ροή αερίου;
- Πώς διαφέρουν οι εξισώσεις συμπιεζόμενης ροής από τη ροή υγρών;
- Ποιοι παράγοντες επηρεάζουν τη συμπεριφορά της ροής αερίου σε βιομηχανικά συστήματα;
- Πώς αλληλεπιδρούν η πίεση, η θερμοκρασία και η ταχύτητα στη ροή αερίου;
- Ποιοι είναι οι διαφορετικοί τύποι καθεστώτων ροής αερίου;
- Πώς να υπολογίσετε και να βελτιστοποιήσετε τη ροή αερίου σε βιομηχανικές εφαρμογές;
- Συμπέρασμα
- Συχνές ερωτήσεις σχετικά με τις αρχές ροής αερίου
Ποιες είναι οι θεμελιώδεις αρχές που διέπουν τη ροή αερίου;
Η ροή αερίου λειτουργεί σύμφωνα με τρεις θεμελιώδεις νόμους διατήρησης που διέπουν κάθε κίνηση ρευστού, αλλά με μοναδικά χαρακτηριστικά λόγω της συμπιεστότητας του αερίου και των μεταβολών της πυκνότητας.
Οι αρχές της ροής των αερίων βασίζονται στη διατήρηση της μάζας (εξίσωση συνέχειας), στη διατήρηση της ορμής (δεύτερος νόμος του Νεύτωνα) και στη διατήρηση της ενέργειας (πρώτος νόμος της θερμοδυναμικής), τροποποιημένες για τη συμπεριφορά των συμπιεζόμενων ρευστών.
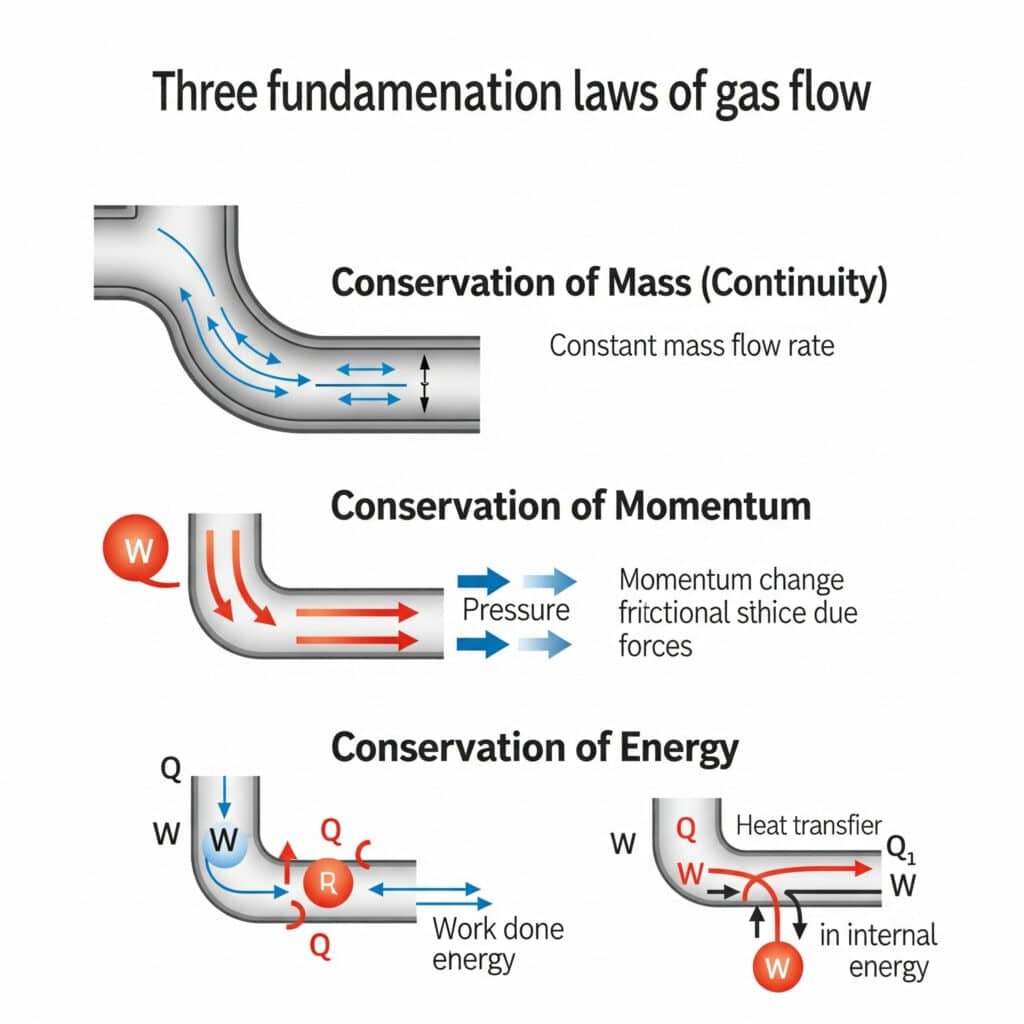
Διατήρηση της μάζας (εξίσωση συνέχειας)
Η εξίσωση συνέχειας για τη ροή αερίου λαμβάνει υπόψη τις μεταβολές της πυκνότητας που συμβαίνουν λόγω μεταβολών της πίεσης και της θερμοκρασίας, σε αντίθεση με τα ασυμπίεστα υγρά.
Εξίσωση συνέχειας ροής αερίου:
∂ρ/∂t + ∇-(ρV) = 0
Για σταθερή ροή: ρ₁A₁V₁ = ρ₂A₂V₂
Πού:
- ρ = Πυκνότητα αερίου (μεταβάλλεται με την πίεση και τη θερμοκρασία)
- A = Εμβαδόν διατομής
- V = ταχύτητα αερίου
- t = Χρόνος
Βασικές επιπτώσεις:
- Η πυκνότητα αερίου μεταβάλλεται με την πίεση και τη θερμοκρασία
- Ο ρυθμός ροής μάζας παραμένει σταθερός σε σταθερή ροή
- Η ταχύτητα αυξάνεται καθώς μειώνεται η πυκνότητα
- Οι αλλαγές στην περιοχή επηρεάζουν τόσο την ταχύτητα όσο και την πυκνότητα
Διατήρηση της ορμής
Η διατήρηση της ορμής στη ροή αερίου λαμβάνει υπόψη τις δυνάμεις πίεσης, τις ιξώδεις δυνάμεις και τις δυνάμεις του σώματος που δρουν στο συμπιεστό ρευστό.
Εξίσωση ορμής (Navier-Stokes2):
ρ(∂V/∂t + V-∇V) = -∇p + μ∇²V + ρg
Για εφαρμογές ροής αερίου:
- Ο όρος της βαθμίδας πίεσης κυριαρχεί στη ροή υψηλής ταχύτητας
- Σημαντικές ιξώδεις επιδράσεις κοντά σε τοιχώματα και σε στρωτή ροή
- Τα φαινόμενα συμπιεστότητας γίνονται σημαντικά πάνω από τα 0,3 Mach
Διατήρηση της ενέργειας
Η διατήρηση της ενέργειας για τη ροή αερίου περιλαμβάνει την κινητική ενέργεια, τη δυνητική ενέργεια, την εσωτερική ενέργεια και το έργο ροής, λαμβάνοντας υπόψη τις μεταβολές της θερμοκρασίας λόγω συμπίεσης και διαστολής.
Εξίσωση ενέργειας:
h + V²/2 + gz = σταθερά (κατά μήκος του ρεύματος)
Πού:
- h = Ειδική ενθαλπία (περιλαμβάνει την εσωτερική ενέργεια και το έργο ροής)
- V²/2 = Κινητική ενέργεια ανά μονάδα μάζας
- gz = Δυνητική ενέργεια ανά μονάδα μάζας
Ενεργειακά ζητήματα:
| Μορφή ενέργειας | Επίδραση ροής αερίου | Τυπικό μέγεθος |
|---|---|---|
| Κινητική ενέργεια | Σημαντικό σε υψηλές ταχύτητες | V²/2 |
| Ενέργεια πίεσης | Κυρίαρχο στις περισσότερες εφαρμογές | p/ρ |
| Εσωτερική ενέργεια | Αλλαγές με τη θερμοκρασία | CᵥT |
| Εργασία ροής | Απαιτείται για την κίνηση αερίου | pv |
Εξίσωση της κατάστασης
Η ροή αερίου απαιτεί μια καταστατική εξίσωση για να συσχετίσει την πίεση, την πυκνότητα και τη θερμοκρασία, συνήθως τον νόμο του ιδανικού αερίου για τις περισσότερες βιομηχανικές εφαρμογές.
Νόμος του ιδανικού αερίου:
ρ = ρRT
Πού:
- p = Απόλυτη πίεση
- ρ = Πυκνότητα αερίου
- R = Ειδική σταθερά αερίου
- T = Απόλυτη θερμοκρασία
Για πραγματικά αέρια, μπορεί να απαιτούνται πιο πολύπλοκες καταστατικές εξισώσεις, όπως οι εξισώσεις van der Waals ή Redlich-Kwong.
Πώς διαφέρουν οι εξισώσεις συμπιεζόμενης ροής από τη ροή υγρών;
Η συμπιεστή ροή αερίων παρουσιάζει θεμελιωδώς διαφορετική συμπεριφορά από την ασυμπίεστη ροή υγρών, απαιτώντας εξειδικευμένες μεθόδους ανάλυσης και σχεδιασμού.
Η συμπιεστή ροή διαφέρει μέσω των μεταβολών της πυκνότητας, των περιορισμών της ηχητικής ταχύτητας, του σχηματισμού κρουστικών κυμάτων και της σύζευξης θερμοκρασίας-πίεσης που δεν εμφανίζονται στα ασυμπίεστα συστήματα ροής υγρών.
Επιδράσεις της διακύμανσης της πυκνότητας
Η πυκνότητα του αερίου μεταβάλλεται σημαντικά με την πίεση και τη θερμοκρασία, επηρεάζοντας τα μοτίβα ροής, τις κατανομές ταχύτητας και τις απαιτήσεις σχεδιασμού του συστήματος.
Επιπτώσεις αλλαγής πυκνότητας:
- Ταχύτητα Επιτάχυνση: Το αέριο επιταχύνεται καθώς διαστέλλεται
- Πτώση πίεσης: Μη γραμμικές σχέσεις πίεσης-ροής
- Επιδράσεις της θερμοκρασίας: Πυκνότητα αντιστρόφως ανάλογη της θερμοκρασίας
- Πνιγμένη ροή: Περιορισμοί μέγιστου ρυθμού ροής
Ηχητική ταχύτητα και αριθμός Mach
Η συμπεριφορά της ροής των αερίων αλλάζει δραματικά καθώς η ταχύτητα πλησιάζει την ταχύτητα του ήχου, δημιουργώντας κρίσιμους σχεδιαστικούς περιορισμούς που δεν υπάρχουν στα συστήματα υγρών.
Υπολογισμός ηχητικής ταχύτητας:
α = √(γRT)
Πού:
- a = Ταχύτητα του ήχου στο αέριο
- γ = λόγος ειδικής θερμότητας (Cp/Cv)
- R = Ειδική σταθερά αερίου
- T = Απόλυτη θερμοκρασία
Αριθμός Mach3 Σημασία:
M = V/a (Λόγος ταχύτητας προς ηχητική ταχύτητα)
| Εύρος Mach | Καθεστώς ροής | Χαρακτηριστικά |
|---|---|---|
| M < 0.3 | Ασυμπίεστο | Πυκνότητα ουσιαστικά σταθερή |
| 0.3 < M < 1.0 | Υποηχητικό Συμπιεστό | Σημαντικές αλλαγές στην πυκνότητα |
| M = 1.0 | Sonic | Κρίσιμες συνθήκες ροής |
| M > 1.0 | Υπερηχητικό | Πιθανά κρουστικά κύματα |
Φαινόμενο πνιγμένης ροής
Πνιγμένη ροή4 εμφανίζεται όταν η ταχύτητα του αερίου φτάνει σε ηχητικές συνθήκες, περιορίζοντας τη μέγιστη παροχή ανεξάρτητα από τη μείωση της πίεσης κατάντη.
Συνθήκες πνιγμένης ροής:
- Μέγιστη επιτευχθείσα ροή μάζας
- Οι μεταβολές της πίεσης κατάντη δεν επηρεάζουν τη ροή ανάντη
- Κρίσιμος λόγος πίεσης: p₂/p₁ ≈ 0,53 για τον αέρα
- Συνήθως σε ακροφύσια, στόμια και βαλβίδες ελέγχου
Σύζευξη θερμοκρασίας-πίεσης
Η ροή αερίου συνεπάγεται σημαντικές μεταβολές της θερμοκρασίας λόγω διαστολής και συμπίεσης, που επηρεάζουν την απόδοση και το σχεδιασμό του συστήματος.
Θερμοδυναμικές διεργασίες:
- Ισεντροπική ροή: Αντιστρεπτή, αδιαβατική διαδικασία
- Ισοθερμική ροή: Σταθερή θερμοκρασία (αργή ροή με μεταφορά θερμότητας)
- Αδιαβατική ροή: Καμία μεταφορά θερμότητας (ταχεία ροή)
- Πολυτροπική ροή: Γενική περίπτωση με μεταφορά θερμότητας
Ποιοι παράγοντες επηρεάζουν τη συμπεριφορά της ροής αερίου σε βιομηχανικά συστήματα;
Πολλαπλοί παράγοντες επηρεάζουν τη συμπεριφορά της ροής αερίου σε βιομηχανικές εφαρμογές, απαιτώντας ολοκληρωμένη ανάλυση για τον κατάλληλο σχεδιασμό και λειτουργία του συστήματος.
Στους βασικούς παράγοντες περιλαμβάνονται οι ιδιότητες του αερίου, η γεωμετρία του συστήματος, οι συνθήκες λειτουργίας, τα αποτελέσματα της μεταφοράς θερμότητας και η τριβή των τοιχωμάτων που καθορίζουν συλλογικά τα πρότυπα ροής, τις πτώσεις πίεσης και την απόδοση του συστήματος.
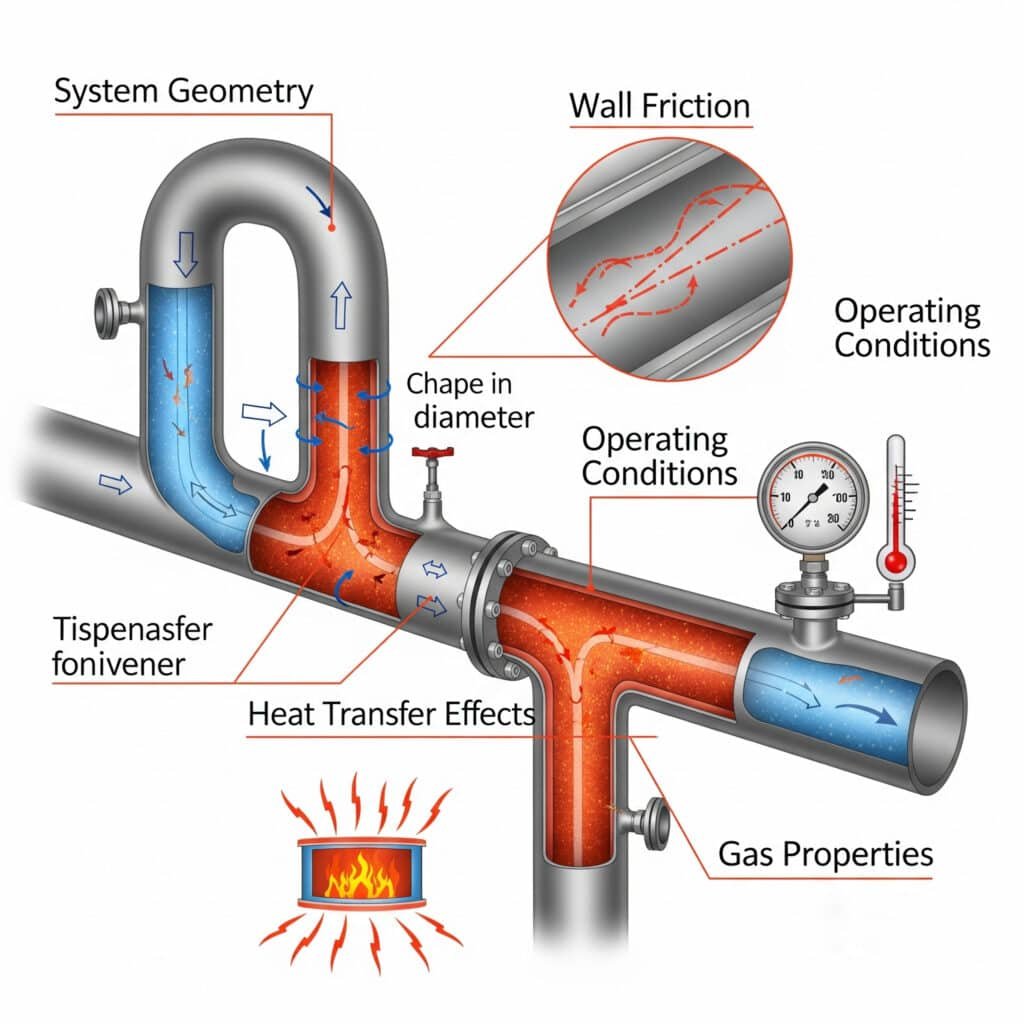
Ιδιότητες αερίου Επιπτώσεις
Τα διάφορα αέρια παρουσιάζουν διαφορετικά χαρακτηριστικά ροής με βάση τις μοριακές τους ιδιότητες, τους λόγους ειδικής θερμότητας και τη θερμοδυναμική τους συμπεριφορά.
Κρίσιμες ιδιότητες αερίου:
| Ακίνητα | Σύμβολο | Επίδραση στη ροή | Τυπικές τιμές |
|---|---|---|---|
| Λόγος ειδικής θερμότητας | γ | Ηχητική ταχύτητα, διαστολή | 1.4 (αέρας), 1.3 (CO₂) |
| Αέριο Σταθερά | R | Σχέση πυκνότητας-πίεσης | 287 J/kg-K (αέρας) |
| Ιξώδες | μ | Απώλειες τριβής | 1,8×10-⁵ Pa-s (αέρας) |
| Μοριακό βάρος | M | Πυκνότητα σε δεδομένες συνθήκες | 29 kg/kmol (αέρας) |
Αποτελέσματα γεωμετρίας συστήματος
Η διάμετρος του σωλήνα, το μήκος, τα εξαρτήματα και οι αλλαγές στην περιοχή ροής επηρεάζουν σημαντικά τα πρότυπα ροής αερίου και τις απώλειες πίεσης.
Σκέψεις γεωμετρίας:
- Διάμετρος σωλήνα: Επηρεάζει την ταχύτητα και τις απώλειες τριβής
- Μήκος: Προσδιορίζει τη συνολική πτώση πίεσης τριβής
- Αλλαγές περιοχής: Δημιουργία εφέ επιτάχυνσης/επιβράδυνσης
- Εξαρτήματα: Προκαλούν τοπικές απώλειες πίεσης
- Επιφανειακή τραχύτητα: Επηρεάζει τον παράγοντα τριβής
Πίεση και θερμοκρασία λειτουργίας
Οι συνθήκες λειτουργίας του συστήματος επηρεάζουν άμεσα την πυκνότητα του αερίου, το ιξώδες και τη συμπεριφορά ροής μέσω θερμοδυναμικών σχέσεων.
Επιπτώσεις κατάστασης λειτουργίας:
- Υψηλή πίεση: Αυξάνει την πυκνότητα, μειώνει τα φαινόμενα συμπιεστότητας
- Χαμηλή πίεση: Μειώνει την πυκνότητα, αυξάνει την ταχύτητα
- Υψηλή θερμοκρασία: Μειώνει την πυκνότητα, αυξάνει την ηχητική ταχύτητα
- Χαμηλή θερμοκρασία: Αυξάνει την πυκνότητα, μπορεί να προκαλέσει συμπύκνωση
Επιπτώσεις μεταφοράς θερμότητας
Η προσθήκη ή αφαίρεση θερμότητας κατά τη ροή αερίου επηρεάζει σημαντικά τις κατανομές θερμοκρασίας, πυκνότητας και πίεσης.
Σενάρια μεταφοράς θερμότητας:
- Θέρμανση: Αυξάνει τη θερμοκρασία, μειώνει την πυκνότητα, επιταχύνει τη ροή
- Ψύξη: Μειώνει τη θερμοκρασία, αυξάνει την πυκνότητα, επιβραδύνει τη ροή
- Αδιαβατικό: Καμία μεταφορά θερμότητας, αλλαγές θερμοκρασίας λόγω διαστολής/συμπίεσης
- Ισόθερμο: Σταθερή θερμοκρασία που διατηρείται μέσω της μεταφοράς θερμότητας
Αντίκτυπος τριβής τοίχου
Η τριβή μεταξύ του αερίου και των τοιχωμάτων του σωλήνα δημιουργεί απώλειες πίεσης και επηρεάζει τα προφίλ ταχύτητας, γεγονός ιδιαίτερα σημαντικό σε αγωγούς μεγάλου μήκους.
Υπολογισμός απωλειών τριβής:
Δp = f × (L/D) × (ρV²/2)
Πού:
- f = συντελεστής τριβής (συνάρτηση του αριθμού Reynolds και της τραχύτητας)
- L = Μήκος σωλήνα
- D = Διάμετρος σωλήνα
- ρ = Πυκνότητα αερίου
- V = ταχύτητα αερίου
Πώς αλληλεπιδρούν η πίεση, η θερμοκρασία και η ταχύτητα στη ροή αερίου;
Η αλληλεπίδραση μεταξύ πίεσης, θερμοκρασίας και ταχύτητας στη ροή αερίου δημιουργεί πολύπλοκες σχέσεις που πρέπει να γίνουν κατανοητές για τον κατάλληλο σχεδιασμό και ανάλυση του συστήματος.
Οι αλληλεπιδράσεις της ροής αερίου ακολουθούν θερμοδυναμικές σχέσεις όπου οι μεταβολές της πίεσης επηρεάζουν τη θερμοκρασία και την πυκνότητα, οι μεταβολές της ταχύτητας επηρεάζουν την πίεση μέσω των φαινομένων ορμής και οι μεταβολές της θερμοκρασίας επηρεάζουν όλες τις άλλες ιδιότητες μέσω της καταστατικής εξίσωσης.
Σχέσεις πίεσης-ταχύτητας
Η ταχύτητα και η πίεση του αερίου συνδέονται αντιστρόφως ανάλογα μέσω της εξίσωσης του Bernoulli, τροποποιημένης για συμπιεστή ροή, δημιουργώντας μοναδικές προκλήσεις στο σχεδιασμό.
Τροποποιημένη εξίσωση Bernoulli για ροή αερίου:
∫dp/ρ + V²/2 + gz = σταθερά
Για ιδανικό αέριο: γ/(γ-1) × (p/ρ) + V²/2 = σταθερά
Επιδράσεις πίεσης-ταχύτητας:
- Πτώση πίεσης: Προκαλεί αύξηση της ταχύτητας λόγω διαστολής του αερίου
- Αύξηση ταχύτητας: Μπορεί να προκαλέσει πρόσθετη πτώση πίεσης μέσω των φαινομένων ορμής
- Επιτάχυνση: Εμφανίζεται φυσικά καθώς το αέριο διαστέλλεται μέσω του συστήματος
- Επιβράδυνση: Απαιτεί αύξηση της πίεσης ή επέκταση της περιοχής
Σύζευξη θερμοκρασίας-ταχύτητας
Η θερμοκρασία και η ταχύτητα του αερίου συνδέονται μέσω της διατήρησης της ενέργειας, με τις μεταβολές της θερμοκρασίας να επηρεάζουν τις ιδιότητες του αερίου και τη συμπεριφορά της ροής.
Σχέσεις θερμοκρασίας-ταχύτητας:
T₀ = T + V²/(2Cp)
Πού:
- T₀ = θερμοκρασία στασιμότητας (συνολική)
- T = Στατική θερμοκρασία
- V = ταχύτητα αερίου
- Cp = Ειδική θερμότητα σε σταθερή πίεση
Πρακτικές επιπτώσεις:
- Η ροή αερίου υψηλής ταχύτητας μειώνει τη στατική θερμοκρασία
- Η θερμοκρασία στασιμότητας παραμένει σταθερή στην αδιαβατική ροή
- Οι μεταβολές της θερμοκρασίας επηρεάζουν την πυκνότητα και το ιξώδες του αερίου
- Η ψύξη μπορεί να προκαλέσει συμπύκνωση σε ορισμένα αέρια
Επιδράσεις πίεσης-θερμοκρασίας
Η πίεση και η θερμοκρασία αλληλεπιδρούν μέσω της καταστατικής εξίσωσης και των θερμοδυναμικών διεργασιών, επηρεάζοντας την πυκνότητα του αερίου και τα χαρακτηριστικά ροής.
Θερμοδυναμικές σχέσεις διεργασιών:
| Τύπος διαδικασίας | Σχέση πίεσης-θερμοκρασίας | Εφαρμογή |
|---|---|---|
| Ισεντροπική | p/p₀ = (T/T₀)^(γ/(γ-1)) | Ακροφύσια, διαχύτες |
| Ισόθερμο | pV = σταθερό, T = σταθερό | Αργή ροή με μεταφορά θερμότητας |
| Ισοβαρικό | p = σταθερό | Θέρμανση σταθερής πίεσης |
| Ισοχωρική | V = σταθερό | Θέρμανση σταθερού όγκου |
Μεταβολές πυκνότητας
Η πυκνότητα του αερίου μεταβάλλεται τόσο με την πίεση όσο και με τη θερμοκρασία σύμφωνα με τον νόμο του ιδανικού αερίου, δημιουργώντας πολύπλοκη συμπεριφορά ροής.
Υπολογισμός πυκνότητας:
ρ = ρ/(RT)
Επίδραση της πυκνότητας στη ροή:
- Υψηλή πυκνότητα: Χαμηλότερη ταχύτητα για δεδομένη ροή μάζας
- Χαμηλή πυκνότητα: Υψηλότερη ταχύτητα, πιθανές επιδράσεις συμπιεστότητας
- Διαβαθμίσεις πυκνότητας: Δημιουργήστε εφέ άντωσης και ανάμιξης
- Αλλαγές πυκνότητας: Επηρεάζουν τη μεταφορά ορμής και ενέργειας
Πρόσφατα βοήθησα έναν Αμερικανό μηχανικό φυσικού αερίου ονόματι Robert Chen στο Τέξας να βελτιστοποιήσει το σύστημα αγωγών του. Με την κατάλληλη συνεκτίμηση των αλληλεπιδράσεων θερμοκρασίας-πίεσης-ταχύτητας, μειώσαμε την ενέργεια άντλησης κατά 28%, ενώ αυξήσαμε τη χωρητικότητα διέλευσης κατά 15%.
Ποιοι είναι οι διαφορετικοί τύποι καθεστώτων ροής αερίου;
Η ροή αερίου παρουσιάζει διαφορετικά καθεστώτα ανάλογα με την ταχύτητα, τις συνθήκες πίεσης και τη γεωμετρία του συστήματος, που απαιτούν συγκεκριμένες μεθόδους ανάλυσης και σχεδιαστικές εκτιμήσεις.
Τα καθεστώτα ροής αερίου περιλαμβάνουν στρωτή, τυρβώδη, υποηχητική, ηχητική και υπερηχητική ροή, που χαρακτηρίζονται από διαφορετικά προφίλ ταχύτητας, σχέσεις πίεσης και χαρακτηριστικά μεταφοράς θερμότητας.
Στρωτή έναντι τυρβώδους ροής
Μεταβάσεις ροής αερίου από στρωτή σε τυρβώδη με βάση Αριθμός Reynolds5, που επηρεάζουν τις απώλειες πίεσης, τη μεταφορά θερμότητας και τα χαρακτηριστικά ανάμιξης.
Αριθμός Reynolds για ροή αερίου:
Re = ρVD/μ
Πού:
- ρ = Πυκνότητα αερίου (μεταβάλλεται με την πίεση και τη θερμοκρασία)
- V = Μέση ταχύτητα
- D = Διάμετρος σωλήνα
- μ = Δυναμικό ιξώδες
Ταξινόμηση καθεστώτων ροής:
| Αριθμός Reynolds | Καθεστώς ροής | Χαρακτηριστικά |
|---|---|---|
| Re < 2300 | Laminar | Ομαλή, προβλέψιμη ροή |
| 2300 < Re < 4000 | Μετάβαση | Ασταθής, μικτή συμπεριφορά |
| Re > 4000 | Τυρβώδης | Χαοτική, ενισχυμένη ανάμιξη |
Υποηχητικό καθεστώς ροής
Η υποηχητική ροή εμφανίζεται όταν η ταχύτητα του αερίου είναι μικρότερη από την τοπική ταχύτητα του ήχου, επιτρέποντας τη διάδοση των διαταραχών της πίεσης προς τα πάνω.
Χαρακτηριστικά υποηχητικής ροής:
- Αριθμός Mach: M < 1.0
- Διάδοση πίεσης: Οι διαταραχές ταξιδεύουν προς τα ανάντη
- Έλεγχος ροής: Οι κατάντη συνθήκες επηρεάζουν ολόκληρο το σύστημα
- Αλλαγές πυκνότητας: Μέτριες, προβλέψιμες διακυμάνσεις
- Ευελιξία σχεδιασμού: Πιθανές πολλαπλές λύσεις
Εφαρμογές υποηχητικής ροής:
- Τα περισσότερα βιομηχανικά συστήματα διανομής αερίου
- Συστήματα HVAC και εξαερισμού
- Πνευματικά συστήματα χαμηλής πίεσης
- Εξοπλισμός χημικών διεργασιών
- Χειρισμός αερίου σταθμού παραγωγής ηλεκτρικής ενέργειας
Ηχητική ροή (πνιγμένη ροή)
Η ηχητική ροή εμφανίζεται όταν η ταχύτητα του αερίου ισούται με την τοπική ταχύτητα του ήχου, δημιουργώντας κρίσιμες συνθήκες ροής με μοναδικά χαρακτηριστικά.
Ιδιότητες ηχητικής ροής:
- Αριθμός Mach: M = 1.0 ακριβώς
- Μέγιστη ροή μάζας: Δεν μπορεί να ξεπεραστεί
- Ανεξαρτησία πίεσης: Η κατάντη πίεση δεν επηρεάζει τη ροή
- Κρίσιμος λόγος πίεσης: Συνήθως περίπου 0,53 για τον αέρα
- Επιδράσεις της θερμοκρασίας: Σημαντική πτώση θερμοκρασίας
Εφαρμογές ηχητικής ροής:
- Ακροφύσια αεριοστροβίλων
- Βαλβίδες ασφαλείας
- Συσκευές μέτρησης ροής
- Ακροφύσια πυραυλοκινητήρων
- Ρυθμιστές αερίου υψηλής πίεσης
Υπερηχητικό καθεστώς ροής
Η υπερηχητική ροή εμφανίζεται όταν η ταχύτητα του αερίου υπερβαίνει την ταχύτητα του ήχου, δημιουργώντας κρουστικά κύματα και μοναδικά φαινόμενα ροής.
Χαρακτηριστικά υπερηχητικής ροής:
- Αριθμός Mach: M > 1.0
- Κρουστικά κύματα: Ξαφνικές αλλαγές πίεσης και θερμοκρασίας
- Κατεύθυνση ροής: Οι πληροφορίες δεν μπορούν να ταξιδέψουν προς τα πάνω
- Κύματα επέκτασης: Ομαλή μείωση της πίεσης
- Πολυπλοκότητα σχεδιασμού: Απαιτεί εξειδικευμένη ανάλυση
Τύποι κρουστικών κυμάτων:
| Τύπος κλονισμού | Χαρακτηριστικά | Εφαρμογές |
|---|---|---|
| Κανονικό σοκ | Κάθετα στη ροή | Διαχυτήρες, εισόδους |
| Οβελιαίο σοκ | Υπό γωνία προς την κατεύθυνση της ροής | Υπερηχητικά αεροσκάφη |
| Ανεμιστήρας επέκτασης | Σταδιακή μείωση της πίεσης | Σχεδιασμός ακροφυσίου |
Υπερηχητική ροή
Η υπερηχητική ροή εμφανίζεται σε πολύ υψηλούς αριθμούς Mach (συνήθως M > 5), όπου πρόσθετες επιδράσεις καθίστανται σημαντικές.
Υπερηχητικές επιδράσεις:
- Πραγματικές επιδράσεις αερίου: Ο νόμος των ιδανικών αερίων καταρρέει
- Χημικές αντιδράσεις: Διάσπαση και ιονισμός
- Μεταφορά θερμότητας: Ακραία αποτελέσματα θέρμανσης
- Ιξώδη αποτελέσματα: Αλληλεπιδράσεις οριακού στρώματος
Πώς να υπολογίσετε και να βελτιστοποιήσετε τη ροή αερίου σε βιομηχανικές εφαρμογές;
Οι υπολογισμοί ροής αερίου απαιτούν εξειδικευμένες μεθόδους που λαμβάνουν υπόψη τα φαινόμενα συμπιεστότητας, ενώ η βελτιστοποίηση επικεντρώνεται στην ελαχιστοποίηση της κατανάλωσης ενέργειας και τη μεγιστοποίηση της απόδοσης του συστήματος.
Οι υπολογισμοί ροής αερίου χρησιμοποιούν εξισώσεις συμπιεζόμενης ροής, συσχετίσεις συντελεστών τριβής και θερμοδυναμικές σχέσεις, ενώ η βελτιστοποίηση περιλαμβάνει τη διαστασιολόγηση των σωλήνων, την επιλογή του επιπέδου πίεσης και τη διαμόρφωση του συστήματος για την ελαχιστοποίηση του ενεργειακού κόστους.
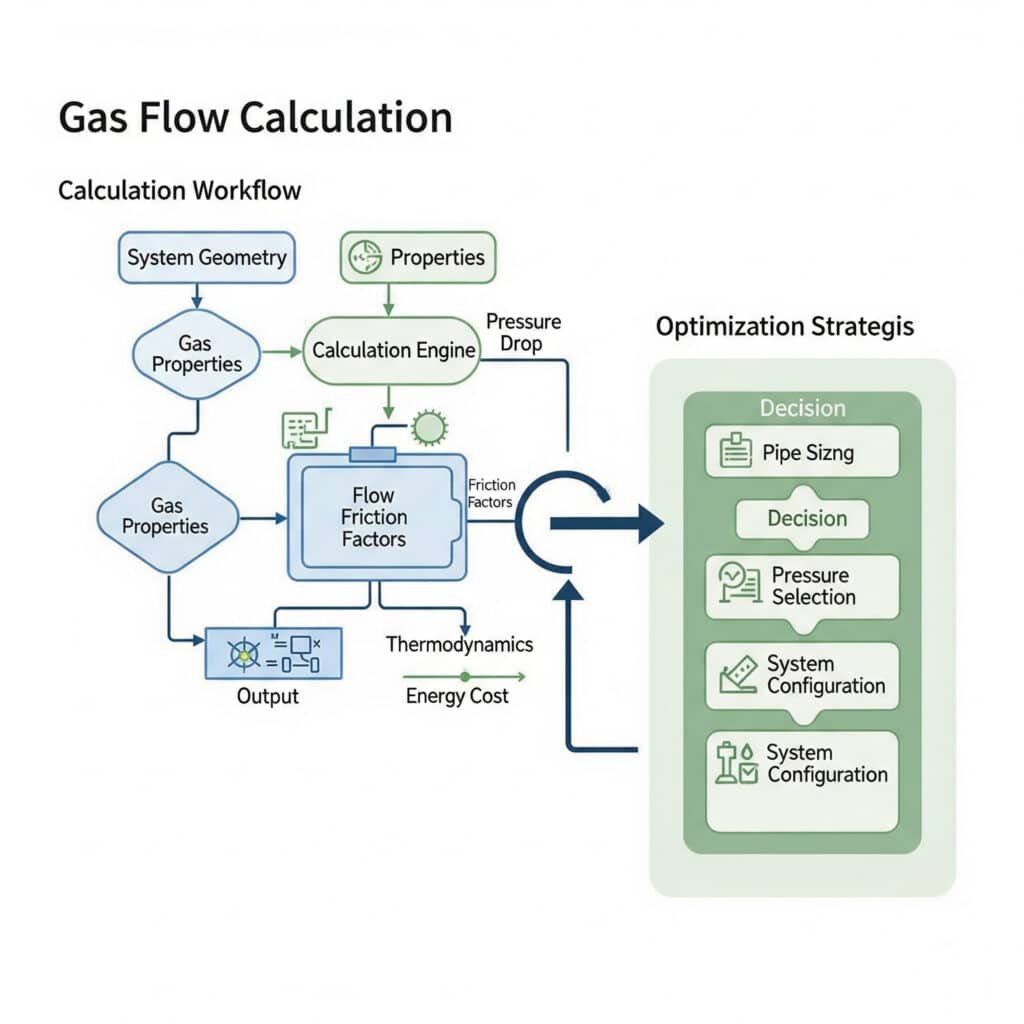
Βασικοί υπολογισμοί ροής αερίου
Οι υπολογισμοί ροής αερίου ξεκινούν με θεμελιώδεις εξισώσεις τροποποιημένες για τα φαινόμενα συμπιεζόμενης ροής και τις πραγματικές ιδιότητες του αερίου.
Υπολογισμός ρυθμού ροής μάζας:
ṁ = ρAV = (p/RT)AV
Για πνιγμένη ροή μέσω ενός στομίου:
ṁ = CdA√(γρp)[2/(γ+1)]^((γ+1)/(2(γ-1))
Πού:
- Cd = Συντελεστής εκφόρτισης
- A = Εμβαδόν στομίου
- γ = Λόγος ειδικής θερμότητας
- ρ = Πυκνότητα ανάντη
- p = Πίεση ανάντη
Υπολογισμοί πτώσης πίεσης
Οι υπολογισμοί της πτώσης πίεσης για τη ροή αερίου πρέπει να λαμβάνουν υπόψη τα φαινόμενα επιτάχυνσης που οφείλονται στη διαστολή του αερίου εκτός από τις απώλειες τριβής.
Συνολικά στοιχεία πτώσης πίεσης:
- Πτώση πίεσης τριβής: Λόγω της διατμητικής τάσης του τοιχώματος
- Επιτάχυνση Πτώση πίεσης: Λόγω αύξησης της ταχύτητας
- Πτώση πίεσης ανύψωσης: Λόγω βαρυτικών επιδράσεων
- Πτώση πίεσης τοποθέτησης: Λόγω διαταραχών της ροής
Τύπος πτώσης πίεσης τριβής:
Δpf = f(L/D)(ρV²/2)
Πτώση πίεσης επιτάχυνσης:
Δπα = ρ₂V₂² - ρ₁V₁² (για αλλαγές περιοχής)
Ανάλυση ροής αγωγών
Η ανάλυση αγωγών μεγάλου μήκους απαιτεί επαναληπτικούς υπολογισμούς λόγω των μεταβαλλόμενων ιδιοτήτων του αερίου κατά μήκος του αγωγού.
Βήματα υπολογισμού αγωγών:
- Αγωγός διαχωρισμού: Σε τμήματα με σταθερές ιδιότητες
- Υπολογισμός ιδιοτήτων τμήματος: Πίεση, θερμοκρασία, πυκνότητα
- Καθορισμός του καθεστώτος ροής: Στρωτή ή τυρβώδης
- Υπολογίστε την πτώση πίεσης: Για κάθε τμήμα
- Ενημέρωση ιδιοτήτων: Για το επόμενο τμήμα
- Επανάληψη: Μέχρι να επιτευχθεί σύγκλιση
Απλοποιημένη εξίσωση αγωγών:
p₁² - p₂² = (fLṁ²RT)/(A²Dρ₀)
Πού:
- p₁, p₂ = Πιέσεις εισόδου και εξόδου
- f = Μέσος συντελεστής τριβής
- L = Μήκος αγωγού
- ṁ = Ρυθμός ροής μάζας
- R = Σταθερά αερίου
- T = Μέση θερμοκρασία
- A = Εμβαδόν σωλήνα
- D = Διάμετρος σωλήνα
- ρ₀ = Πυκνότητα αναφοράς
Στρατηγικές βελτιστοποίησης συστήματος
Η βελτιστοποίηση του συστήματος ροής αερίου εξισορροπεί το κόστος κεφαλαίου, το λειτουργικό κόστος και τις απαιτήσεις απόδοσης για την επίτευξη ελάχιστου κόστους κύκλου ζωής.
Παράμετροι βελτιστοποίησης:
| Παράμετρος | Επίδραση στο σύστημα | Στρατηγική βελτιστοποίησης |
|---|---|---|
| Διάμετρος σωλήνα | Κόστος κεφαλαίου σε σχέση με την πτώση πίεσης | Υπολογισμός οικονομικής διαμέτρου |
| Πίεση λειτουργίας | Κόστος συμπίεσης έναντι κόστους σωλήνα | Βελτιστοποίηση επιπέδου πίεσης |
| Σταδιοποίηση συμπιεστή | Αποδοτικότητα έναντι πολυπλοκότητας | Βελτιστοποίηση αριθμού σταδίων |
| Μέγεθος εναλλάκτη θερμότητας | Ανάκτηση θερμότητας έναντι κόστους κεφαλαίου | Οικονομική ανταλλαγή θερμότητας |
Οικονομική διαστασιολόγηση σωλήνων
Η οικονομική διαστασιολόγηση των σωλήνων εξισορροπεί το κόστος κεφαλαίου των σωλήνων έναντι του κόστους ενέργειας άντλησης κατά τη διάρκεια ζωής του συστήματος.
Τύπος οικονομικής διαμέτρου:
D_economic = K(ṁ/ρ)^0,37
Όπου το Κ εξαρτάται από:
- Ενεργειακό κόστος
- Κόστος σωλήνων
- Διάρκεια ζωής του συστήματος
- Επιτόκιο
- Ώρες λειτουργίας ανά έτος
Μέτρηση και έλεγχος ροής
Η ακριβής μέτρηση και ο έλεγχος της ροής αερίου απαιτούν την κατανόηση των επιδράσεων της συμπιεζόμενης ροής στις συσκευές μέτρησης.
Σκέψεις μέτρησης ροής:
- Πλάκες οπών: Απαιτούνται διορθώσεις συμπιεστότητας
- Μετρητές Venturi: Λιγότερο ευαίσθητη στη συμπιεστότητα
- Μετρητές τουρμπίνας: Επηρεάζεται από τις μεταβολές της πυκνότητας του αερίου
- Μετρητές υπερήχων: Απαιτείται αντιστάθμιση θερμοκρασίας
- Μετρητές Coriolis: Άμεση μέτρηση ροής μάζας
Υπολογιστική Δυναμική Ρευστών (CFD)
Τα πολύπλοκα συστήματα ροής αερίου επωφελούνται από την ανάλυση CFD για τη βελτιστοποίηση της απόδοσης και την πρόβλεψη της συμπεριφοράς σε διάφορες συνθήκες λειτουργίας.
Εφαρμογές CFD:
- Πολύπλοκες γεωμετρίες: Ακανόνιστα σχήματα και εξαρτήματα
- Μεταφορά θερμότητας: Συνδυασμένη ανάλυση ροής και θερμική ανάλυση
- Ανάλυση ανάμειξης: Μεταβολές της σύνθεσης των αερίων
- Βελτιστοποίηση: Μελέτες παραμέτρων σχεδιασμού
- Αντιμετώπιση προβλημάτων: Προσδιορισμός προβλημάτων ροής
Πρόσφατα συνεργάστηκα με έναν Καναδό μηχανικό πετροχημικών με το όνομα David Wilson στην Αλμπέρτα, του οποίου η μονάδα επεξεργασίας φυσικού αερίου αντιμετώπιζε προβλήματα απόδοσης. Χρησιμοποιώντας ανάλυση CFD σε συνδυασμό με κατάλληλους υπολογισμούς ροής αερίου, εντοπίσαμε ζώνες ανακυκλοφορίας που προκαλούσαν σπατάλη ενέργειας 20%. Μετά την εφαρμογή τροποποιήσεων στο σχεδιασμό, η κατανάλωση ενέργειας μειώθηκε κατά 18%, ενώ παράλληλα αυξήθηκε η ικανότητα επεξεργασίας.
Συμπέρασμα
Οι αρχές της ροής των αερίων διέπουν τη συμπεριφορά των συμπιεζόμενων ρευστών μέσω νόμων διατήρησης που τροποποιούνται για τις μεταβολές της πυκνότητας, απαιτώντας εξειδικευμένες μεθόδους ανάλυσης που λαμβάνουν υπόψη τις αλληλεπιδράσεις πίεσης-θερμοκρασίας-ταχύτητας και τις επιδράσεις συμπιεστότητας που διαφέρουν θεμελιωδώς από τα συστήματα ροής υγρών.
Συχνές ερωτήσεις σχετικά με τις αρχές ροής αερίου
Ποια είναι η θεμελιώδης αρχή της ροής των αερίων;
Η ροή αερίου λειτουργεί με βάση τη διατήρηση της μάζας, της ορμής και της ενέργειας, τροποποιημένη για τη συμπεριφορά συμπιεζόμενου ρευστού, όπου η πυκνότητα του αερίου μεταβάλλεται με την πίεση και τη θερμοκρασία, δημιουργώντας αλληλεπιδράσεις ταχύτητας-πίεσης-θερμοκρασίας.
Πώς διαφέρει η ροή αερίου από τη ροή υγρού;
Η ροή αερίου περιλαμβάνει σημαντικές μεταβολές της πυκνότητας, περιορισμούς της ηχητικής ταχύτητας, σύζευξη θερμοκρασίας-πίεσης και φαινόμενα πνιγμένης ροής που δεν εμφανίζονται σε ασυμπίεστα συστήματα ροής υγρών.
Τι είναι η στραγγαλισμένη ροή στα συστήματα αερίου;
Πνιγμένη ροή εμφανίζεται όταν η ταχύτητα του αερίου φτάνει σε ηχητικές συνθήκες (Mach = 1,0), περιορίζοντας τη μέγιστη παροχή μάζας ανεξάρτητα από τη μείωση της πίεσης κατάντη, που συνήθως συμβαίνει σε ακροφύσια και βαλβίδες ελέγχου.
Πώς υπολογίζετε τον ρυθμό ροής αερίου;
Ο υπολογισμός του ρυθμού ροής αερίου χρησιμοποιεί την εξίσωση ṁ = ρAV, όπου η πυκνότητα μεταβάλλεται με την πίεση και τη θερμοκρασία σύμφωνα με τον νόμο του ιδανικού αερίου, γεγονός που απαιτεί επαναληπτικές λύσεις για πολύπλοκα συστήματα.
Ποιοι παράγοντες επηρεάζουν τη συμπεριφορά της ροής αερίου;
Στους βασικούς παράγοντες περιλαμβάνονται οι ιδιότητες του αερίου (μοριακό βάρος, λόγος ειδικής θερμότητας), η γεωμετρία του συστήματος (διάμετρος σωλήνων, εξαρτήματα), οι συνθήκες λειτουργίας (πίεση, θερμοκρασία) και τα αποτελέσματα της μεταφοράς θερμότητας.
Γιατί είναι σημαντικός ο αριθμός Mach στη ροή αερίου;
Ο αριθμός Mach (ταχύτητα/ηχητική ταχύτητα) καθορίζει τα χαρακτηριστικά του καθεστώτος ροής: η υποηχητική ροή (Μ1) δημιουργεί κρουστικά κύματα.
-
Εξηγεί τη θεμελιώδη διαφορά μεταξύ της συμπιεζόμενης ροής, όπου η πυκνότητα του ρευστού μεταβάλλεται σημαντικά με την πίεση, και της ασυμπίεστης ροής, όπου η πυκνότητα θεωρείται σταθερή, μια βασική διάκριση μεταξύ της δυναμικής των αερίων και των υγρών. ↩
-
Παρέχει μια επισκόπηση των εξισώσεων Navier-Stokes, ενός συνόλου μερικών διαφορικών εξισώσεων που αποτελούν το θεμέλιο της μηχανικής των ρευστών και περιγράφουν την κίνηση ιξωδών ρευστών ουσιών με βάση τη διατήρηση της ορμής. ↩
-
Προσφέρει έναν λεπτομερή ορισμό του αριθμού Mach, ενός μεγέθους χωρίς διαστάσεις στη δυναμική των ρευστών που αντιπροσωπεύει το λόγο της ταχύτητας ροής που περνάει από ένα όριο προς την τοπική ταχύτητα του ήχου, ο οποίος χρησιμοποιείται για την ταξινόμηση των καθεστώτων ροής. ↩
-
Περιγράφει το φαινόμενο της πνιγμένης ροής, μια οριακή κατάσταση στη συμπιεστή ροή, όπου η παροχή μάζας δεν αυξάνεται με περαιτέρω μείωση της πίεσης κατάντη, καθώς η ταχύτητα στο στενότερο σημείο έχει φθάσει την ταχύτητα του ήχου. ↩
-
Εξηγεί τον αριθμό Reynolds, ένα κρίσιμο μέγεθος χωρίς διαστάσεις στη μηχανική των ρευστών που χρησιμοποιείται για την πρόβλεψη των προτύπων ροής, βοηθώντας στη διάκριση μεταξύ στρωτής (ομαλής) και τυρβώδους (χαοτικής) ροής. ↩


