Mis on absoluutne rõhk ja kuidas see mõjutab pneumaatilise süsteemi jõudlust?

Rõhu mõõtmine ajab isegi kogenud insenerid segadusse. Olen leidnud lugematul hulgal pneumaatikasüsteeme, kus ebaõiged rõhureferentsid on põhjustanud töövõime probleeme. Absoluutse rõhu mõistmine hoiab ära kulukad arvutusvead ja süsteemirikked.

Absoluutne rõhk (ABS-rõhk) mõõdab rõhku võrreldes täiusliku vaakumiga, mis hõlmab mõõtmisel ka õhurõhku. See on võrdne mõõterõhu ja atmosfäärirõhu (14,7 PSI merepinna kõrgusel) väärtusega, mis annab pneumaatilistele komponentidele mõjuva tegeliku kogurõhu.

Eelmisel nädalal aitasin Thomasel, Hollandi tootmisettevõtte projekteerimisinseneril, lahendada kõrgusega seotud probleemid tema vardata pneumosilinder¹ süsteem. Tema arvutused toimisid suurepäraselt merepinna kõrgusel, kuid nende mägiruumides ebaõnnestusid. Probleem ei olnud mitte seadmete rike, vaid absoluutse rõhu väärarusaam.

Sisukord

• Mis on absoluutne rõhk ja kuidas see erineb mõõturirõhust?
• Miks on absoluutne rõhk pneumaatiliste arvutuste jaoks kriitiline?
• Kuidas mõjutab kõrgus absoluutset rõhku pneumaatilistes süsteemides?
• Millised on absoluutse rõhu tavalised rakendused tööstuses?
• Kuidas teisendada erinevate rõhu mõõtmiste vahel?
• Milliseid vigu teevad insenerid absoluutse rõhu arvutamisel?

Mis on absoluutne rõhk ja kuidas see erineb mõõturirõhust?

Absoluutne rõhk kujutab süsteemile mõjuvat kogurõhku, mis on mõõdetud täiuslikust vaakumi võrdluspunktist. See mõõtmine hõlmab atmosfäärirõhu mõju, mida mõõturõhk ei võta arvesse.

Absoluutne rõhk on võrdne mõõturõhu ja atmosfäärirõhuga. Merepinnal on atmosfäärirõhk 14,7 PSI, seega 80 PSIG mõõturirõhk võrdub 94,7 PSIA absoluutse rõhuga. See erinevus on pneumaatikasüsteemi täpsete arvutuste jaoks ülioluline.

Rõhu võrdluspunktide mõistmine

Erinevad rõhu mõõtmised kasutavad erinevaid võrdluspunkte:

Surve tüüp	Võrdluspunkt	Sümbol	Tüüpiline vahemik
Absoluutne	Täiuslik vaakum	PSIA	0 kuni 1000+ PSIA
Mõõtja	Atmosfääriline	PSIG	-14,7 kuni 1000+ PSIG
Diferentsiaal	Kahe punkti vahel	PSID	Muutuv
Vaakum	Allpool atmosfääri	"Hg	0 kuni 29,92 "Hg

Absoluutse rõhu alused

Absoluutne rõhk annab täieliku pildi rõhu kohta. See hõlmab nii rakendatud rõhku kui ka süsteemi ümbritsevat õhurõhku.

Põhiline suhe on:
PSIA = PSIG + atmosfäärirõhk

Standardsetel merepinnatingimustel:
PSIA = PSIG + 14,7

Mõõturi rõhu piirangud

Manomeetrilise rõhu mõõtmisel ei võeta arvesse õhurõhu muutusi. See tekitab probleeme, kui õhurõhk muutub kõrguse või ilmastikutingimuste tõttu.

Enamiku tööstuslike rakenduste puhul on mõõturõhk hea, sest õhurõhk püsib fikseeritud kohtades suhteliselt konstantne. Absoluutne rõhk muutub aga kriitiliseks järgmistel juhtudel:

• Kõrguse kompenseerimise arvutused
• Vaakumsüsteemi projekteerimine
• Gaasiseaduse rakendused
• Voolukiiruse arvutused
• Temperatuuri kompenseerimine

Praktilised mõõtmiserinevused

Töötasin hiljuti koos Annaga, kes on Norra avamereplatvormi protsessiinsener. Tema pneumaatilised arvutused toimisid suurepäraselt maismaal, kuid ebaõnnestusid, kui seadmed viidi üle merel toimuvatele operatsioonidele.

Probleemiks oli õhurõhu kõikumine. Ilmastikusüsteemid tekitasid 1-2 PSI õhurõhu muutusi, mis mõjutasid tema mõõturirõhu näitu. Üleminekuga absoluutse rõhu mõõtmisele kõrvaldasime ilmastikuoludest tingitud jõudluse kõikumised.

Visuaalne mõistmine

Mõelge absoluutsest rõhust kui mõõtmisest basseini põhjast (täiuslik vaakum) kuni veepinnani (süsteemirõhk). Manomeetriline rõhk mõõdab ainult tavalise veetaseme (atmosfäärirõhu) ja veepinna vahelist rõhku.

See võrdlus aitab mõista, miks absoluutne rõhk annab tehnilistes arvutustes täielikumad andmed.

Miks on absoluutne rõhk pneumaatiliste arvutuste jaoks kriitiline?

Absoluutne rõhk on aluseks täpsetele pneumaatiliste süsteemide arvutustele. Paljud tehnilised valemid nõuavad õigete tulemuste saamiseks absoluutse rõhu väärtusi.

Absoluutne rõhk on pneumaatiliste arvutuste jaoks hädavajalik, sest gaasiseadused, voolu võrrandid ja termodünaamilised seosed kasutavad absoluutse rõhu väärtusi. Mõõdurõhu kasutamine nendes valemites annab ebaõigeid tulemusi, mis võivad põhjustada süsteemi rikkeid.

Gaasiseaduse rakendused

The ideaalse gaasi seadus² nõuab täpsete arvutuste tegemiseks absoluutset rõhku:

PV = nRT

Kus:

• P = absoluutne rõhk
• V = ruumala
• n = moolide arv
• R = gaasikonstant
• T = Absoluutne temperatuur³

Mõõdurõhu kasutamine gaasiseaduse arvutustes tekitab vigu, mis on proportsionaalsed atmosfäärirõhuga. Meretasandil tekitab see enamikus arvutustes 15% vea.

Vooluhulga arvutused

Pneumaatilise vooluhulga valemite jaoks on vaja absoluutset rõhu suhet:

Vooluhulk ∝ √(P₁² - P₂²)

Kus P₁ ja P₂ on absoluutsed rõhud enne ja pärast piirangut.

Mõõdurõhu kasutamine vooluhulga arvutustes võib põhjustada vigu, mis ületavad 20%, mis viib süsteemi komponentide alamõõdulisele või üledimensioneeritud mõõtmetele.

Silindri jõuarvutused

Kui põhilised jõuarvutused (F = P × A) töötavad manomeetrilise rõhuga, siis edasijõudnud rakendused nõuavad absoluutset rõhku:

Kõrguse kompenseerimine

Õhusurve muutuste tõttu muutub jõu väljund kõrgus merepinnast. Absoluutse rõhu arvutustes võetakse need muutused arvesse.

Temperatuuri mõju

Gaasi paisumise ja kokkutõmbumise arvutused nõuavad täpsuse tagamiseks absoluutse rõhu ja temperatuuri väärtusi.

Kompressori jõudlus

Kompressori suuruse ja jõudluse arvutamisel kasutatakse absoluutse rõhu suhtarvu:

Kompressioonisuhe = P₂(abs) ÷ P₁(abs)

See suhe määrab kompressori astme nõuded ja energiatarbimise. Mõõdurõhu kasutamine tekitab ebaõige tihendussuhted⁴.

Reaalse maailma näide

Ma aitasin Marcusel, Šveitsi täppisehituse hooldusjuhil, lahendada ebajärjekindlaid vardata silindrite töötulemusi. Tema rajatis töötas 3000 jalga kõrgusel, kus õhurõhk on 13,2 PSI, mitte 14,7 PSI nagu merepinnal.

Tema manomeetrirõhu näit näitas 80 PSIG, kuid absoluutne rõhk oli oodatud 94,7 PSIA asemel ainult 93,2 PSIA. See 1,5 PSI erinevus vähendas silindri jõu väljundit 1,6% võrra, põhjustades positsioneerimistäpsuse probleeme täppisrakendustes.

Tema arvutusi kohaliku õhurõhu jaoks ümberkalibreerides taastasime süsteemi nõuetekohase toimimise.

Vaakumrakendused

Vaakumsüsteemid nõuavad absoluutse rõhu mõõtmist, sest rõhk muutub negatiivseks allpool atmosfäärirõhku:

Vaakum tase	Mõõtja rõhk	Absoluutne rõhk
Raua vaakum	-10 PSIG	4.7 PSIA
Keskmine vaakum	-13 PSIG	1.7 PSIA
Kõrge vaakum	-14,5 PSIG	0,2 PSIA
Täiuslik vaakum	-14,7 PSIG	0,0 PSIA

Kuidas mõjutab kõrgus absoluutset rõhku pneumaatilistes süsteemides?

Kõrgus mõjutab oluliselt õhurõhku, mis mõjutab pneumosüsteemi jõudlust. Nende mõjude mõistmine hoiab ära tulemuslikkuse probleemid kõrgendatud paigaldistes.

Atmosfäärirõhk väheneb umbes 0,5 PSI iga 1000 jala kõrguse tõusu kohta. See vähenemine mõjutab absoluutse rõhu arvutusi ja võib vähendada pneumosilindri jõu väljundit 3-4% võrra 1000 jala kõrguse kohta.

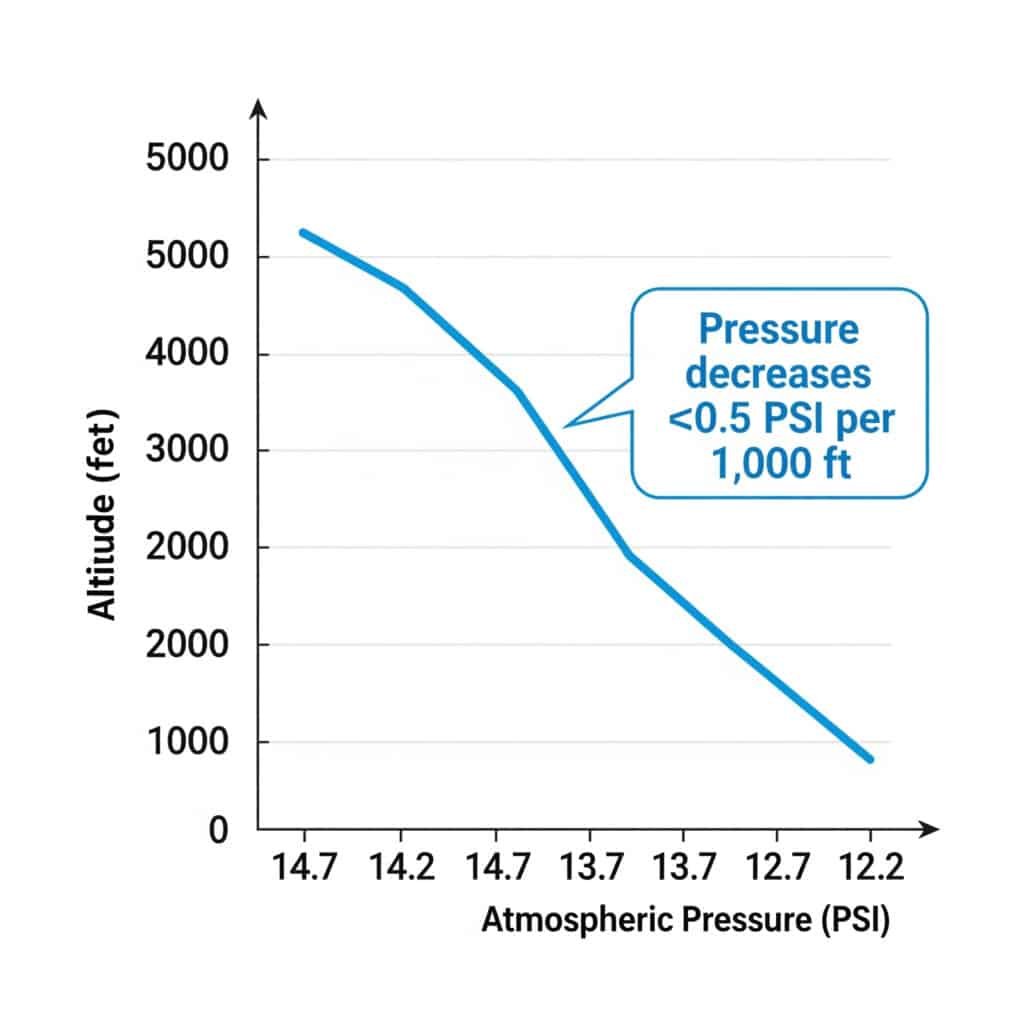
Atmosfäärirõhk vs. kõrgus merepinnast

Standardne õhurõhk varieerub prognoositavalt kõrguse järgi:

Kõrgus merepinnast (jalad)	Atmosfäärirõhk (PSIA)	Rõhu vähendamine
Meretase	14.7	0%
1,000	14.2	3.4%
2,000	13.7	6.8%
5,000	12.2	17.0%
10,000	10.1	31.3%

Jõu väljund mõju

Vähenenud õhurõhk mõjutab silindri jõuarvutusi, kui kasutatakse absoluutset rõhku:

Efektiivne rõhk = mõõturirõhk + kohalik õhurõhk

Ballooni puhul, mis töötab 80 PSIG juures:

• Meretase: 80 + 14,7 = 94,7 PSIA
• 5000 jalga: 80 + 12,2 = 92,2 PSIA
• Jõu vähendamine: 2.6%

Kõrguse kompenseerimise strateegiad

Mitmed meetodid kompenseerivad kõrguse mõju:

Rõhu reguleerimine

Suurendage mõõturirõhku, et säilitada konstantne absoluutne rõhk:
Vajalik mõõturirõhk = absoluutne sihtrõhk - kohalik atmosfäärirõhk

Süsteemi ümberkujundamine

Muuda balloonide suurust, et säilitada jõu väljund vähendatud absoluutse rõhu tingimustes.

Juhtimissüsteemi kompenseerimine

Programmeerida juhtimissüsteemid kohaliku õhurõhu muutuste kohandamiseks.

Temperatuuri ja kõrguse kombineeritud mõju

Nii kõrgus kui ka temperatuur mõjutavad õhutihedust ja süsteemi jõudlust:

Õhutihedus = (absoluutne rõhk × molekulmass) ÷ (gaasikonstant × absoluutne temperatuur)

Kõrgemal on tavaliselt madalamad temperatuurid, mis osaliselt tasakaalustab rõhu vähenemise mõju õhutihedusele.

Reaalse maailma kõrguse rakendus

Töötasin koos Carlosega, kes oli projektijuht, kes paigaldas pneumaatilisi süsteeme Peruus, 12 000 jalga kõrgusel asuvas kaevandusettevõttes. Tema arvutused merepinnast näitasid piisavat jõudu materjalide käitlemise rakenduste jaoks.

Paigalduskõrgusel oli õhurõhk ainult 9,3 PSIA võrreldes merepinna 14,7 PSIA-ga. See 37% atmosfäärirõhu vähenemine mõjutas oluliselt süsteemi jõudlust.

Me kompenseerisime:

• Töörõhu tõstmine 80-lt 95 PSIG-le
• Kriitiliste silindrite suurendamine 15% võrra
• Rõhu suurendajate lisamine suure jõudlusega rakenduste jaoks

Muudetud süsteem andis nõutava tulemuse, hoolimata äärmuslikest kõrgustingimustest.

Ilmastiku mõju kõrgusel

Kõrgel asuvates kohtades on ilmastikurõhu kõikumine ilmastiku tõttu suurem:

Meretaseme muutused

• Kõrgsurve: 15,2 PSIA (+0,5 PSI)
• Madal rõhk: 14,2 PSIA (-0,5 PSI)
• Kokku vahemik: 1.0 PSI

Kõrgusevariatsioonid (10 000 jalga)

• Kõrgsurve: 10,6 PSIA (+0,5 PSI)
• Madal rõhk: 9,6 PSIA (-0,5 PSI)
• Kokku vahemik: 1,0 PSI (10% alusrõhu kohta)

Millised on absoluutse rõhu tavalised rakendused tööstuses?

Absoluutse rõhu mõõtmine on hädavajalik paljudes tööstusrakendustes, kus täpsed rõhusuhted määravad süsteemi jõudluse ja ohutuse.

Tavalised absoluutse rõhu rakendused hõlmavad vaakumsüsteeme, gaasivoolu arvutusi, kompressorite dimensioneerimist, kõrguse kompenseerimist ja termodünaamilisi protsesse. Need rakendused nõuavad absoluutset rõhku, sest mõõtmisrõhu mõõtmine annab ebatäielikku teavet.

Vaakumsüsteemi projekteerimine

Vaakumrakendused nõuavad absoluutse rõhu mõõtmist, sest rõhk muutub negatiivseks allpool atmosfääritingimusi:

Vaakumpumba suuruse määramine

Vaakumpumba võimsus sõltub absoluutsest rõhu suhtest:
Pumpamiskiirus = mahuvooluhulk ÷ (P₁ - P₂)

Kus P₁ ja P₂ on absoluutsed rõhud pumba sisse- ja väljavoolu juures.

Vaakumtaseme spetsifikatsioonid

Tööstuslike vaakumtasemete puhul kasutatakse absoluutse rõhu mõõtmist:

Taotlus	Vaakumtase (PSIA)	Tüüpiline kasutamine
Materjalide käitlemine	10-12	iminapad, konveierid
Pakend	5-8	Vaakumpakendamine
Töötlev tööstus	1-3	Destilleerimine, kuivatamine
Laboratoorium	0.1-0.5	Uurimisrakendused

Gaasivoolu mõõtmine

Gaasivoolu täpsed arvutused nõuavad absoluutse rõhu väärtusi:

Tardunud voolu tingimused

Gaasivool lämbub, kui allavoolu rõhk langeb alla kriitilise rõhu:
Kriitiline rõhu suhe = 0,528 (õhu puhul)

See arvutus nõuab absoluutset rõhku, et määrata voolupiirangud.

Massivoolu arvutused

Massivoolukiirus sõltub absoluutsest rõhust ja temperatuurist:
Massivool = (absoluutne rõhk × pindala × kiirus) ÷ (gaasikonstant × absoluutne temperatuur)

Kompressori rakendused

Kompressori mõõtmisel ja jõudluse määramisel kasutatakse absoluutset rõhu suhet:

Kompressioonisuhte arvutused

Kompressioonisuhe = väljastusrõhk (abs) ÷ imemisrõhk (abs)

See suhe määrab:

• Vajalike tihendusastmete arv
• Energiatarbimine
• Tühjendustemperatuur
• Tõhususe näitajad

Kompressori jõudluskaardid

Tootja tulemuslikkuse kaardid kasutavad täpseks valikuks ja kasutamiseks absoluutse rõhu tingimusi.

Protsessi juhtimise rakendused

Paljud protsessijuhtimissüsteemid nõuavad absoluutse rõhu mõõtmist:

Tiheduse arvutused

Gaasi tiheduse arvutused voolu mõõtmiseks ja reguleerimiseks:
Tihedus = (absoluutne rõhk × molekulmass) ÷ (gaasikonstant × absoluutne temperatuur)

Soojusülekande arvutused

Soojusvahetite ja protsessiseadmete termodünaamilistes arvutustes kasutatakse absoluutse rõhu ja temperatuuri väärtusi.

Reaalse protsessi rakendamine

Hiljuti abistasin Elenat, Saksa keemiaettevõtte protsessiinseneri, kes on pneumaatiline transport⁵ süsteemi disain. Tema süsteem transpordib plastpelleteid suruõhu abil läbi kõrgendatud torustike.

Edastusarvutused nõudsid absoluutse rõhu väärtuste määramist:

• Õhutihedus torujuhtme eri kõrgustes
• Rõhulanguse arvutused läbi vertikaalsete lõikude
• Nõuded materjali kiirusele
• Süsteemi võimsuse piirangud

Mõõdurõhu kasutamine oleks tekitanud 15-20% vead transpordivõimsuse arvutustes, mis oleks viinud seadmete alamõõduliseks jäämiseni ja kehva jõudluseni.

Kvaliteedikontrolli rakendused

Täppistootmine nõuab sageli absoluutse rõhu mõõtmist:

Lekke testimine

Absoluutse rõhu mõõtmine võimaldab täpsemat lekke tuvastamist:
Lekke kiirus = maht × rõhu langus ÷ aeg

Absoluutse rõhu kasutamine välistab õhurõhu kõikumised, mis mõjutavad mõõterõhu näitu.

Kalibreerimisstandardid

Rõhu kalibreerimisstandardid kasutavad absoluutse rõhu referentsväärtusi täpsuse ja jälgitavuse tagamiseks.

Kuidas teisendada erinevate rõhu mõõtmiste vahel?

Erinevate mõõtmissüsteemide vaheline rõhu teisendamine nõuab võrdluspunktide ja teisendustegurite mõistmist. Täpsed ümberarvestused hoiavad ära arvutusvigu rahvusvahelistes projektides.

Rõhu teisendamiseks tuleb absoluut- ja mõõtemõõtmiste vahel vahetamisel lisada või lahutada atmosfäärirõhk ning kohaldada ühikute teisendustegureid. Tavalised ümberarvestused hõlmavad PSIA ümberarvestamist baariks, PSIG ümberarvestamist kPa-deks ja vaakummõõtmisi absoluutseks rõhuks.

Põhilised ümberarvestusvalemid

Põhiline suhe rõhu tüüpide vahel:

Absoluutne rõhk = mõõturõhk + õhurõhk
Mõõturõhk = absoluutne rõhk - atmosfäärirõhk
Vaakum = Atmosfäärirõhk - absoluutne rõhk

Ühikute ümberarvestustegurid

Tavalised rõhuühikute teisendused:

Alates	aadressile	Korruta
PSI	baar	0.06895
baar	PSI	14.504
PSI	kPa	6.895
kPa	PSI	0.1450
PSI	"Hg	2.036
"Hg	PSI	0.4912

Atmosfäärirõhu standardid

Atmosfäärirõhu standardväärtused ümberarvestusteks:

Asukoht/standard	Rõhu väärtus
Meretaseme standard	14,696 PSIA, 1,01325 baari
Tehniline standard	14,7 PSIA, 1,013 baari
Metriline standard	101,325 kPa, 760 mmHg

Ümberehituse näited

PSIG to PSIA konverteerimine

80 PSIG kuni PSIA merepinnal:
80 PSIG + 14,7 = 94,7 PSIA

Baari mõõtur to Baari absoluutne

5 barg kuni bara merepinnal:
5 barg + 1,013 = 6,013 bara

Vaakum kuni absoluutne rõhk

25 "Hg vaakum PSIA-le:
14,7 - (25 × 0,4912) = 2,42 PSIA

Rahvusvahelise üksuse kaalutlused

Erinevad riigid kasutavad erinevaid rõhuühikuid:

Piirkond	Ühised üksused	Standardne atmosfääriline
USA	PSIG, PSIA	14,7 PSI
Euroopa	bar, kPa	1,013 baari
Aasia	MPa, kgf/cm²	1,033 kgf/cm²
Teaduslik	Pa, kPa	101,325 kPa

Ümberarvestuse täpsusega seotud kaalutlused

Ümberarvestuse täpsus sõltub õhurõhu eeldustest:

Standard- vs. tegelikud tingimused

• Standard: Kasutab 14,7 PSI atmosfäärirõhku.
• Tegelik: Kasutab kohalikku õhurõhku
• Viga: Võib olla 1-3% sõltuvalt asukohast ja ilmastikuoludest.

Temperatuuri mõju

Atmosfäärirõhk varieerub vastavalt temperatuurile ja ilmastikutingimustele. Täpsete ümberarvestuste tegemiseks kasutage pigem tegelikku kohalikku õhurõhku kui standardväärtusi.

Digitaalsed teisendusvahendid

Kaasaegsed surveseadmed pakuvad sageli automaatset ühikute teisendamist. Kuid käsitsi teisendamise põhimõtete mõistmine aitab kontrollida digitaalsete näitude õigsust ja kõrvaldada teisendusvigu.

Praktiline muundamise rakendus

Töötasin koos Jean-Pierre'iga, Prantsuse autotööstuse tarnija projektiinseneriga, ülemaailmse projekti pneumaatikasüsteemi spetsifikatsioonide kallal. Tema Euroopa spetsifikatsioonides kasutati bar-mõõdurõhku, kuid Põhja-Ameerika paigaldus nõudis PSIG-väärtusi.

Konversiooniprotsessi kaasatud:

1. Euroopa spetsifikatsioon: 6 barg töörõhk
2. Teisenda absoluutseks: 6 + 1,013 = 7,013 bara
3. Teisenda üksused: 7,013 × 14,504 = 101,7 PSIA
4. Teisenda mõõtühikuks: 101,7 - 14,7 = 87,0 PSIG

Selline süstemaatiline lähenemisviis tagas täpsed rõhu spetsifikatsioonid erinevate mõõtesüsteemide puhul ja hoidis ära seadmete mõõtmisvead.

Milliseid vigu teevad insenerid absoluutse rõhu arvutamisel?

Absoluutse rõhu arvutusvead on tavalised ja võivad põhjustada olulisi probleeme süsteemi jõudluses. Nende vigade mõistmine aitab vältida kulukaid projekteerimis- ja käitamisprobleeme.

Tavaliste absoluutse rõhu vigade hulka kuuluvad mõõterõhu kasutamine gaasiseaduse arvutustes, atmosfäärirõhu muutuste eiramine, ebaõige ühikute teisendamine ja vaakumi mõõtmise vääritimõistmine. Need vead põhjustavad tavaliselt 10-30% arvutuste ebatäpsusi ja süsteemi töövõime probleeme.

Mõõdurõhu kasutamine gaasiseaduse arvutustes

Kõige tavalisem viga on kasutada absoluutset rõhku nõudvates valemites mõõturvet:

Gaasiseaduse ebaõige kohaldamine

Vale: PV = nRT, kasutades mõõterõhku
Õige: PV = nRT kasutades absoluutset rõhku

See viga tekitab arvutusvigu, mis on proportsionaalsed õhurõhuga - ligikaudu 15% merepinna tasemel.

Atmosfäärirõhu muutuste eiramine

Paljud insenerid eeldavad pidevat 14,7 PSI atmosfäärirõhku sõltumata asukohast või tingimustest:

Asukoha variatsioonid

• Meretase: 14.7 PSIA
• Denver (5,280 ft): 12.2 PSIA
• Viga: 17%, kui kasutatakse merepinna väärtust Denveris.

Ilmamuutused

• Kõrgsurvesüsteem: 15.2 PSIA
• Madalrõhu süsteem: 14.2 PSIA
• Variatsioon: ±3,4% standardist ±3,4%

Väärad ühikute ümberarvestused

Absoluut- ja manomeetrilise rõhu ühikute segamine tekitab märkimisväärseid vigu:

Tavalised muundamise vead

• Lisades 14,7 baromeetri näitude juurde (peaks lisama 1,013).
• Kasutades 14,7 PSI mitte-sea-tasandi kohtades
• Unustades ühikute vahetamisel absoluut- ja mõõtühikute vahel teisendada

Vaakum mõõtmise segadus

Vaakumi mõõtmised ajavad insenerid sageli segadusse, sest need näitavad rõhku, mis on madalam kui atmosfäärirõhk:

Vaakumrõhu suhted

• 29 "Hg Vaakum = 0,76 PSIA (mitte -29 PSIA)
• Täiuslik vaakum = 0 PSIA absoluutne
• Atmosfääriline rõhk = Maksimaalne võimalik vaakum "Hg

Hiljuti aitasin Robertol, ühe Itaalia pakendiettevõtte projekteerimisinseneril, lahendada vaakumsüsteemi jõudlusprobleeme. Tema arvutused näitasid piisavat vaakumpumba võimsust, kuid süsteem ei suutnud saavutada nõutavat vaakumitaset.

Probleemiks oli vaakum mõõtmise segadus. Roberto arvutas pumba nõuded, kasutades -25 PSIG, mitte õiget 1,4 PSIA absoluutset rõhku. Selle vea tõttu tundus pump 18 korda võimsam kui tegelik võimsus.

Temperatuuri kompenseerimise vead

Absoluutse rõhu arvutustes ei võeta sageli arvesse temperatuuri mõju:

Gaasiseaduse temperatuurinõuded

Gaasiseaduse arvutused nõuavad absoluutset temperatuuri (Rankine'i või Kelvini):

• Fahrenheit to Rankine sihikule: °R = °F + 459,67
• Celsius to Kelvin: K = °C + 273,15

Fahrenheiti või Celsiuse temperatuuride kasutamine gaasiseaduse arvutustes tekitab olulisi vigu.

Kõrgusekompensatsiooni järelevalve

Insenerid kasutavad sageli merepinna tasemel atmosfäärirõhku kõrgel asuvate rajatiste puhul:

Kõrgusrõhu vead

10,000 jalga kõrgusel:

• Tegelik atmosfääriline: 10.1 PSIA
• Meretaseme eeldus: 14.7 PSIA
• Viga: 45% absoluutse rõhu ülehindamine

Kompressori suhtarvu arvutamise vead

Kompressioonisuhte arvutamiseks on vaja absoluutset rõhku, kuid insenerid kasutavad sageli mõõturõhku:

Vale tihendussuhe

80 PSIG väljalaske korral, atmosfääriline imemine:

• Vale: 80 ÷ 0 = määratlemata
• Õige: 94.7 ÷ 14.7 = 6.44:1

Voolu arvutamise vead

Vooluhulga arvutused rõhkude vahede abil nõuavad absoluutse rõhu väärtusi:

Vooluga seotud vead (Choked Flow Mistakes)

Kriitilise rõhu suhte arvutused:

• Vale: Mõõdurõhu suhtarvude kasutamine
• Õige: Absoluutse rõhu suhtarvu kasutamine
• Mõju: Võib üle hinnata vooluvõimsust 15-20% võrra.

Ohutussüsteemi projekteerimisvead

Turvaventiili mõõtmine nõuab absoluutse rõhu arvutusi:

Turvaventiili suuruse määramine

Turvaventiili võimsus sõltub absoluutsest rõhu suhtest. Mõõdurõhu kasutamine võib põhjustada alamõõdetud kaitseklapid ja ohutusriskid.

Ennetamise strateegiad

Vältige absoluutse rõhu arvutamise vigu läbi:

Süsteemne lähenemine

1. Vajaliku rõhu tüübi kindlaksmääramine: Määrake, kas arvutamiseks on vaja absoluutset või mõõturirõhku.
2. Kasutage õiget õhurõhku: Kohaldage kohalikku õhurõhku, mitte standardset merepinna taset.
3. Üksuse järjepidevuse kontrollimine: Veenduge, et kõik rõhud kasutavad sama ühikusüsteemi.
4. Topeltkontroll teisenduste üle: Ümberarvestustegurite ja võrdluspunktide kontrollimine

Dokumentatsioonistandardid

• Selgelt märgistada rõhu tüübid: Täpsustage alati PSIA, PSIG, bara, barg
• Riigi võrdlustingimused: Dokumendi atmosfäärirõhu eeldused
• Kaasa konverteerimistabelid: Anda võrdluskoefitsientide ümberarvestuskoefitsiendid

Kokkuvõte

Absoluutne rõhk annab täieliku rõhupildi, mis on oluline pneumaatikasüsteemi täpsete arvutuste jaoks. Absoluutse rõhu põhimõtete mõistmine hoiab ära tavalised arvutusvead ja tagab usaldusväärse vardata silindrisüsteemi toimimise erinevates töötingimustes.

KKK absoluutse rõhu kohta pneumaatilistes süsteemides

1. Tutvuge vardata pneumosilindrite, mida kasutatakse sageli materjalikäitluses ja automatiseerimises, konstruktsiooni ja tööpõhimõtete eeliste kohta. ↩

2. Uurige ideaalgaasi seadust (PV=nRT), mis on põhiline olekuvõrrand, mis kirjeldab gaasi rõhu, mahu ja temperatuuri vahelist seost. ↩

3. Õppige tundma absoluutseid temperatuuriskaalasid, nagu Kelvin ja Rankine, ja miks need on olulised termodünaamiliste ja gaasiseaduste arvutuste jaoks. ↩

4. Mõista, kui oluline on kompressioonisuhe kompressori jõudluse seisukohalt ja kuidas seda arvutatakse absoluutrõhu abil. ↩

5. Avastage, kuidas pneumaatilised transpordisüsteemid töötavad puistematerjalide transportimiseks surugaasi abil tööstusprotsessides. ↩