
Pernahkah Anda memperhatikan getaran misterius pada saluran pneumatik Anda? Atau variasi gaya yang tidak dapat dijelaskan dalam silinder Anda meskipun tekanan suplai stabil? Fenomena ini tidak terjadi secara acak - fenomena ini merupakan hasil dari gelombang tekanan yang merambat melalui sistem Anda, menciptakan efek yang dapat berkisar dari ketidakefisienan kecil hingga kegagalan besar.
Fluktuasi tekanan dalam sistem pneumatik adalah fenomena gelombang yang merambat dengan kecepatan mendekati kecepatan suara1menciptakan efek dinamis termasuk resonansi, gelombang berdiri2dan amplifikasi tekanan. Memahami fluktuasi ini sangat penting karena dapat menyebabkan kelelahan komponen, ketidakstabilan kontrol, dan kehilangan energi sebesar 10-25% dalam sistem industri pada umumnya3.
Bulan lalu, saya memberikan konsultasi untuk pabrik perakitan otomotif di Tennessee di mana sistem penjepitan pneumatik yang kritis mengalami variasi gaya yang terputus-putus meskipun tekanan suplai stabil. Tim pemeliharaan mereka telah mengganti katup, regulator, dan bahkan seluruh unit persiapan udara4 tanpa hasil. Dengan menganalisis dinamika gelombang tekanan - khususnya pola gelombang berdiri di jalur suplai mereka - kami mengidentifikasi bahwa mereka beroperasi pada frekuensi yang menimbulkan gangguan yang merusak pada silinder. Penyesuaian sederhana pada panjang saluran mereka menghilangkan masalah ini dan menyelamatkan mereka dari penundaan produksi selama berminggu-minggu. Izinkan saya menunjukkan kepada Anda bagaimana memahami teori fluktuasi tekanan dapat mengubah keandalan sistem pneumatik Anda.
Daftar Isi
- Kecepatan Perambatan Gelombang: Seberapa Cepat Gangguan Tekanan Menjalar dalam Sistem Anda?
- Verifikasi Gelombang Berdiri: Bagaimana Frekuensi Resonansi Menciptakan Masalah Performa?
- Metode Atenuasi Pulsa: Teknik Apa yang Secara Efektif Meredam Osilasi Tekanan yang Merusak?
- Kesimpulan
- Tanya Jawab Tentang Fluktuasi Tekanan dalam Sistem Pneumatik
Kecepatan Perambatan Gelombang: Seberapa Cepat Gangguan Tekanan Menjalar dalam Sistem Anda?
Memahami seberapa cepat gangguan tekanan merambat melalui sistem pneumatik merupakan hal mendasar untuk memprediksi dan mengendalikan efeknya. Kecepatan rambat menentukan waktu respons sistem, frekuensi resonansi, dan potensi gangguan yang merusak.
Gelombang tekanan dalam sistem pneumatik bergerak dengan kecepatan suara dalam medium gas, yang dapat dihitung menggunakan rumus c = √(γRT), di mana γ adalah rasio panas spesifik, R adalah konstanta gas spesifik, dan T adalah suhu absolut. Untuk udara pada suhu 20°C, ini setara dengan sekitar 343 m/s, meskipun kecepatan ini dimodifikasi oleh beberapa faktor termasuk elastisitas pipa, kompresibilitas gas, dan kondisi aliran.
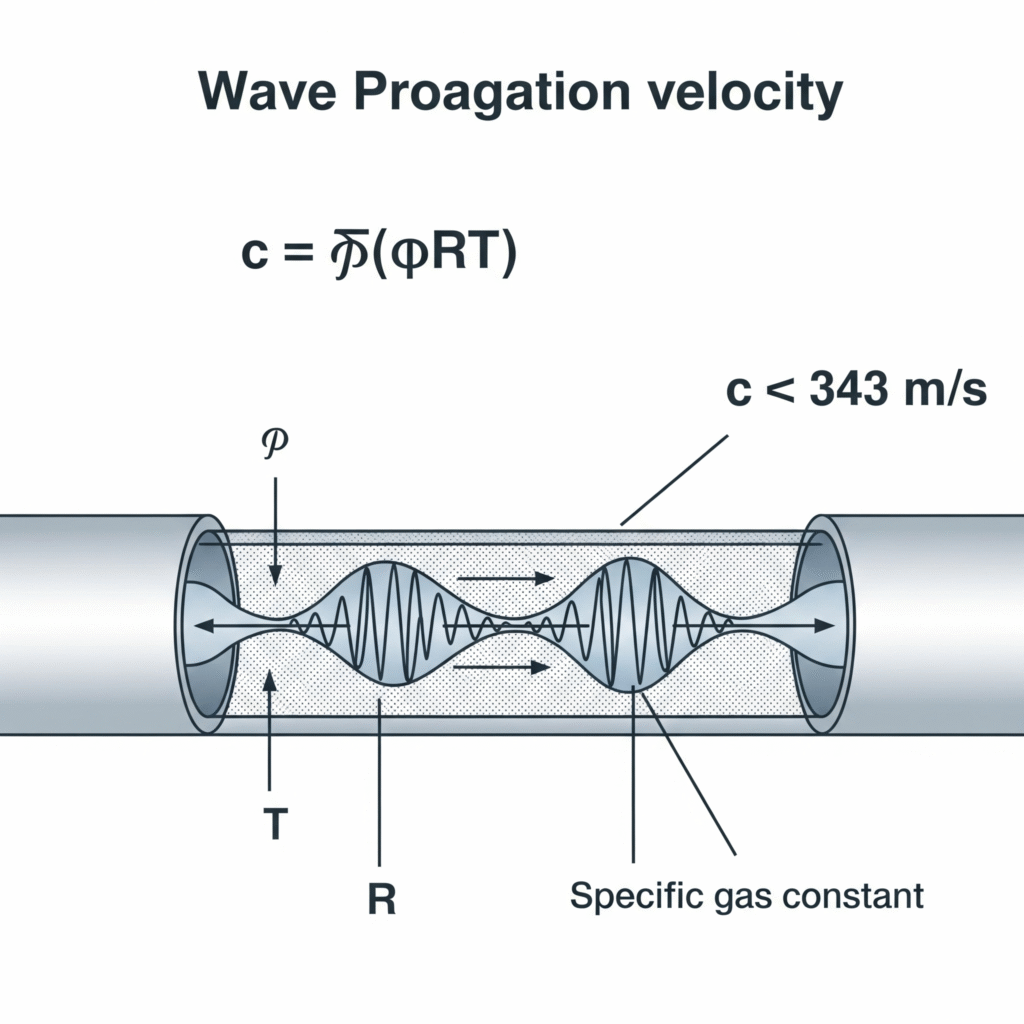
Baru-baru ini saya membantu memecahkan masalah pada mesin perakitan presisi di Swiss, di mana gripper pneumatik mengalami penundaan selama 12 ms antara aktivasi dan aplikasi gaya - suatu hal yang sangat lama dalam lingkungan produksi berkecepatan tinggi. Para insinyur mereka mengasumsikan transmisi tekanan seketika. Dengan mengukur kecepatan rambat gelombang aktual dalam sistem mereka (328 m/s) dan memperhitungkan panjang saluran 4 meter, kami menghitung waktu transmisi teoretis 12,2 ms-hampir sama persis dengan penundaan yang diamati. Memindahkan katup lebih dekat ke aktuator mengurangi penundaan ini menjadi 3ms dan meningkatkan laju produksi sebesar 14%.
Persamaan Kecepatan Gelombang Fundamental
Persamaan dasar untuk kecepatan rambat gelombang tekanan dalam gas adalah:
c = √(γRT)
Dimana:
- c = Kecepatan rambat gelombang (m/s)
- γ = Rasio panas spesifik (1,4 untuk udara)
- R = Konstanta gas spesifik (287 J/kg-K untuk udara)
- T = Suhu absolut (K)
Untuk udara pada suhu 20°C (293K), ini memberikan:
c = √(1,4 × 287 × 293) = 343 m/s
Kecepatan Gelombang yang Dimodifikasi dalam Garis Pneumatik
Dalam sistem pneumatik yang sebenarnya, kecepatan gelombang efektif dimodifikasi oleh elastisitas pipa dan faktor lainnya sesuai dengan rumus:
c_eff = c / √(1 + (Dψ/Eh))
Dimana:
- c_eff = Kecepatan gelombang efektif (m/s)
- D = Diameter pipa (m)
- ψ = Faktor kompresibilitas gas
- E = Modulus elastisitas bahan pipa (Pa)
- h = Ketebalan dinding pipa (m)
Efek Suhu dan Tekanan pada Kecepatan Gelombang
Kecepatan gelombang bervariasi sesuai dengan kondisi pengoperasian:
| Suhu | Tekanan | Kecepatan Gelombang di Udara | Implikasi Praktis |
|---|---|---|---|
| 0°C (273K) | 1 batang | 331 m/s | Respons yang lebih lambat di lingkungan dingin |
| 20°C (293K) | 1 batang | 343 m/s | Kondisi referensi standar |
| 40°C (313K) | 1 batang | 355 m/s | Respons yang lebih cepat di lingkungan yang hangat |
| 20°C (293K) | 6 bar | 343 m/s* | Tekanan memiliki efek langsung yang minimal pada kecepatan |
*Catatan: Meskipun kecepatan gelombang dasar tidak bergantung pada tekanan, kecepatan efektif dalam sistem nyata dapat dipengaruhi oleh perubahan yang disebabkan oleh tekanan pada elastisitas pipa dan perilaku gas.
Perhitungan Waktu Perambatan Gelombang Praktis
Untuk sistem pneumatik dengan:
- Panjang garis (L): 5 meter
- Suhu pengoperasian: 20°C (c = 343 m/s)
- Bahan pipa: Pipa poliuretan (memodifikasi kecepatan sekitar 5%)
Kecepatan gelombang yang efektif adalah:
c_eff = 343 × 0,95 = 326 m/s
Dan waktu perambatan gelombangnya:
t = L/c_eff = 5/326 = 0,0153 detik (15,3 milidetik)
Ini menunjukkan waktu minimum yang diperlukan untuk perubahan tekanan untuk bergerak dari satu ujung saluran ke ujung lainnya-faktor penting dalam aplikasi kecepatan tinggi.
Teknik Pengukuran Kecepatan Gelombang
Beberapa metode dapat digunakan untuk mengukur kecepatan gelombang aktual dalam sistem pneumatik:
Metode Sensor Tekanan Ganda
- Pasang sensor tekanan pada jarak yang diketahui
- Membuat pulsa tekanan (pembukaan katup cepat)
- Mengukur penundaan waktu antara kenaikan tekanan pada setiap sensor
- Hitung kecepatan sebagai jarak dibagi dengan waktu tunda
Metode Frekuensi Resonansi
- Menciptakan osilasi tekanan dalam tabung tertutup
- Mengukur frekuensi resonansi fundamental (f)
- Hitung kecepatan dengan menggunakan c = 2Lf untuk tabung ujung tertutup
- Verifikasi dengan harmonik (kelipatan ganjil dari fundamental)
Metode Pengaturan Waktu Refleksi
- Pasang sensor tekanan di dekat katup
- Buat denyut tekanan dengan membuka katup secara cepat
- Mengukur waktu antara denyut nadi awal dan denyut nadi pantulan
- Hitung kecepatan sebagai 2L dibagi dengan waktu pantulan
Studi Kasus: Dampak Kecepatan Gelombang pada Respons Sistem
Untuk end-effector robotik dengan gripper pneumatik:
| Parameter | Desain Asli (garis 5m) | Desain yang Dioptimalkan (garis 1m) | Peningkatan |
|---|---|---|---|
| Panjang Garis | 5 meter | 1 meter | Pengurangan 80% |
| Waktu Perambatan Gelombang | 15,3 ms | 3,1 ms | 12,2 ms lebih cepat |
| Waktu Peningkatan Tekanan | 28 ms | 9 ms | 19 ms lebih cepat |
| Stabilitas Kekuatan Genggaman | Variasi ±12% | Variasi ±3% | Peningkatan 75% |
| Waktu Siklus | 1,2 detik | 0,95 detik | 21% lebih cepat |
| Tingkat Produksi | 3000 bagian / jam | 3780 bagian/jam | Peningkatan 26% |
Studi kasus ini menunjukkan bagaimana memahami dan mengoptimalkan perambatan gelombang dapat secara signifikan berdampak pada kinerja sistem.
Verifikasi Gelombang Berdiri: Bagaimana Frekuensi Resonansi Menciptakan Masalah Performa?
Gelombang berdiri terjadi ketika gelombang tekanan memantul dan mengganggu diri mereka sendiri, menciptakan pola tetap dari simpul tekanan dan antinoda. Fenomena resonansi ini dapat menyebabkan masalah kinerja yang parah pada sistem pneumatik jika tidak dipahami dan dikelola dengan benar.
Gelombang berdiri dalam sistem pneumatik terjadi ketika gelombang tekanan memantul pada batas dan mengganggu secara konstruktif, menciptakan frekuensi resonansi di mana fluktuasi tekanan diperkuat. Resonansi ini mengikuti rumus f = nc/2L untuk tabung tertutup, di mana n adalah bilangan harmonik, c adalah kecepatan gelombang, dan L adalah panjang tabung. Verifikasi eksperimental melalui sensor tekanan, akselerometer, dan pengukuran akustik mengonfirmasi prediksi teoretis ini dan memandu strategi mitigasi yang efektif.
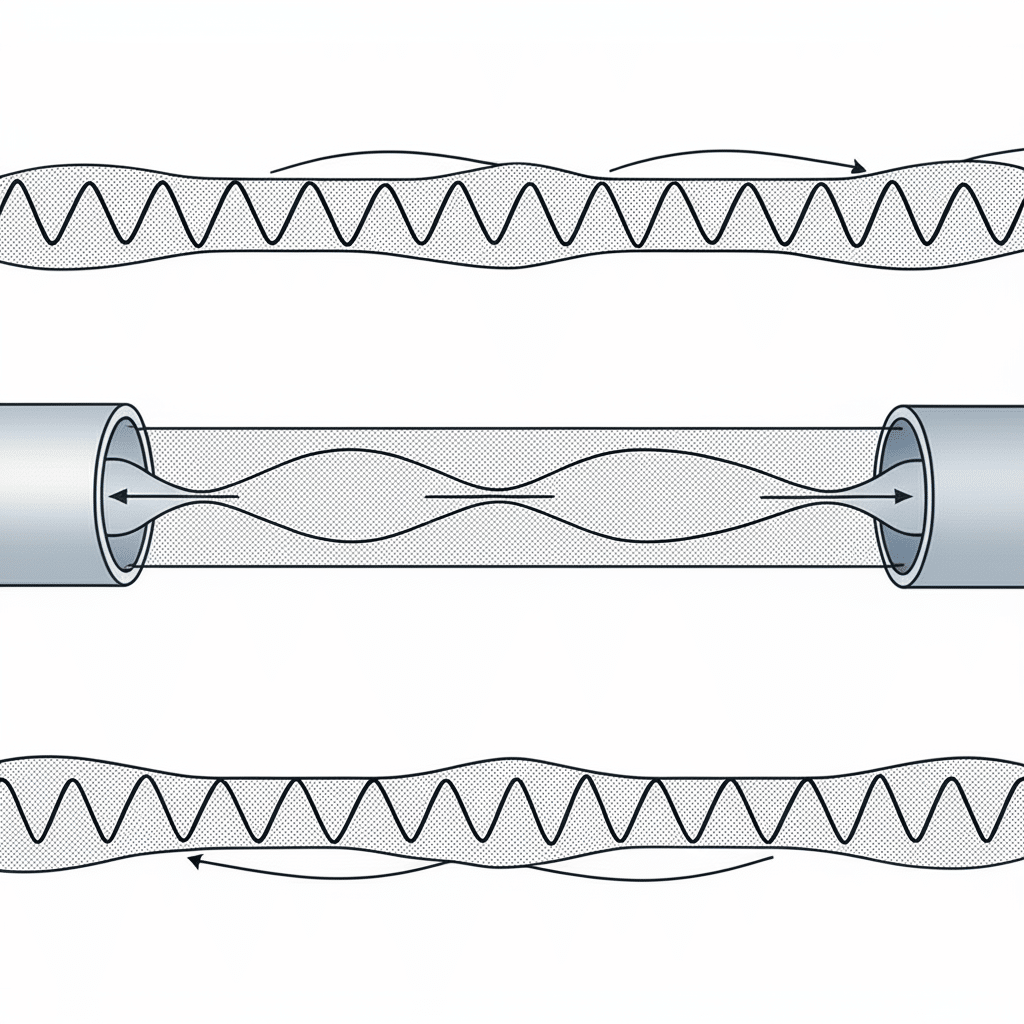
Selama proyek baru-baru ini dengan produsen perangkat medis di Massachusetts, sistem pemosisian pneumatik presisi mereka menunjukkan fluktuasi gaya misterius pada frekuensi operasi tertentu. Dengan melakukan uji verifikasi gelombang berdiri, kami mengidentifikasi bahwa jalur suplai 2,1 meter mereka memiliki resonansi fundamental pada 81 Hz-tepatnya sesuai dengan frekuensi siklus aktuator mereka. Resonansi ini memperkuat fluktuasi tekanan sebesar 320%. Dengan menyesuaikan panjang saluran menjadi 1,8 meter, kami menggeser frekuensi resonansi menjauh dari rentang operasinya dan sepenuhnya menghilangkan masalah, meningkatkan akurasi pemosisian dari ± 0,8 mm menjadi ± 0,15 mm.
Fundamental Gelombang Berdiri
Gelombang berdiri terbentuk ketika gelombang yang datang dan gelombang yang dipantulkan saling berinterferensi, menciptakan pola tetap dari titik-titik tekanan (fluktuasi minimum) dan antinoda (fluktuasi maksimum).
Frekuensi resonansi untuk saluran pneumatik bergantung pada kondisi batas:
Untuk saluran dengan ujung tertutup (paling umum pada sistem pneumatik):
f = nc/2L
Dimana:
- f = Frekuensi resonansi (Hz)
- n = Angka harmonik (1, 2, 3, dst.)
- c = Kecepatan gelombang (m/s)
- L = Panjang garis (m)
Untuk garis dengan satu ujung terbuka:
f = (2n-1)c/4L
Untuk garis dengan kedua ujung terbuka (jarang terjadi pada pneumatik):
f = nc/2L
Metode Verifikasi Eksperimental
Beberapa teknik dapat memverifikasi pola gelombang berdiri dalam sistem pneumatik:
Array Beberapa Sensor Tekanan
- Pasang transduser tekanan secara berkala di sepanjang jalur pneumatik
- Menggairahkan sistem dengan sapuan frekuensi atau impuls
- Catat fluktuasi tekanan di setiap lokasi
- Memetakan amplitudo tekanan vs. posisi untuk mengidentifikasi simpul dan antinode
- Membandingkan frekuensi terukur dengan prediksi teoretis
Korelasi Akustik
- Gunakan sensor akustik (mikrofon) untuk mendeteksi suara dari fluktuasi tekanan
- Menghubungkan intensitas suara dengan frekuensi pengoperasian
- Mengidentifikasi puncak intensitas suara yang sesuai dengan frekuensi resonansi
- Verifikasi bahwa puncak terjadi pada frekuensi yang diprediksi
Pengukuran Akselerometer
- Memasang akselerometer pada saluran dan komponen pneumatik
- Mengukur amplitudo getaran di seluruh rentang frekuensi
- Mengidentifikasi puncak resonansi dalam spektrum getaran
- Berkorelasi dengan frekuensi gelombang berdiri yang diprediksi
Perhitungan Frekuensi Gelombang Berdiri Praktis
Untuk sistem pneumatik tipikal dengan:
- Panjang garis (L): 3 meter
- Kecepatan gelombang (c): 343 m/s
- Konfigurasi ujung tertutup
Frekuensi resonansi fundamental adalah:
f₁ = c/2L = 343/(2×3) = 57,2 Hz
Dan harmoniknya pun demikian:
f₂ = 2f₁ = 114,4 Hz
f₃ = 3f₁ = 171,6 Hz
f₄ = 4f₁ = 228,8 Hz
Frekuensi ini mewakili titik masalah potensial di mana fluktuasi tekanan dapat diperkuat.
Pola Gelombang Berdiri dan Efeknya
| Harmonik | Pola Simpul/Antinode | Efek Sistem | Komponen Kritis yang Terpengaruh |
|---|---|---|---|
| Fundamental (n = 1) | Satu antinoda tekanan di tengah | Variasi tekanan yang besar pada garis tengah | Komponen in-line, alat kelengkapan |
| Kedua (n=2) | Dua antinode, simpul di tengah | Variasi tekanan di dekat ujung | Katup, aktuator, regulator |
| Ketiga (n=3) | Tiga antinode, dua node | Pola tekanan yang kompleks | Beberapa komponen sistem |
| Keempat (n=4) | Empat antinode, tiga node | Osilasi frekuensi tinggi | Segel, komponen kecil |
Studi Kasus Verifikasi Eksperimental
Untuk sistem pemosisian pneumatik presisi yang mengalami kinerja yang tidak konsisten:
| Parameter | Prediksi Teoritis | Pengukuran Eksperimental | Korelasi |
|---|---|---|---|
| Frekuensi Dasar | 81,2 Hz | 79,8 Hz | 98.3% |
| Harmonik Kedua | 162,4 Hz | 160,5 Hz | 98.8% |
| Harmonik Ketiga | 243,6 Hz | 240,1 Hz | 98.6% |
| Amplifikasi Tekanan | 3:1 pada resonansi (perkiraan) | 3.2:1 pada resonansi (terukur) | 93.8% |
| Lokasi Simpul | 0, 1,05, 2,1 meter | 0, 1,08, 2,1 meter | 97.2% |
Studi kasus ini menunjukkan kesepakatan yang sangat baik antara prediksi teoretis dan pengukuran eksperimental fenomena gelombang berdiri.
Implikasi Praktis dari Gelombang Berdiri
Gelombang berdiri menciptakan beberapa masalah signifikan dalam sistem pneumatik:
Amplifikasi Tekanan
- Fluktuasi dapat diperkuat 3-5× pada resonansi
- Dapat melebihi peringkat tekanan komponen
- Menciptakan variasi gaya pada aktuatorKelelahan Komponen
- Siklus tekanan frekuensi tinggi mempercepat keausan seal
- Getaran menyebabkan pelonggaran dan kebocoran pada fitting
- Mengurangi masa pakai sistem hingga 30-70% dalam kasus yang parahKetidakstabilan Kontrol
- Sistem umpan balik dapat berosilasi pada frekuensi resonansi
- Kontrol posisi dan gaya menjadi tidak dapat diprediksi
- Dapat menciptakan osilasi yang memperkuat diri sendiriKehilangan Energi
- Gelombang berdiri mewakili energi yang terperangkap
- Dapat meningkatkan konsumsi energi sebesar 10-30%
- Mengurangi efisiensi sistem secara keseluruhan
Metode Atenuasi Pulsa: Teknik Apa yang Secara Efektif Meredam Osilasi Tekanan yang Merusak?
Mengontrol fluktuasi tekanan sangat penting untuk pengoperasian sistem pneumatik yang andal. Berbagai metode atenuasi dapat digunakan untuk mengurangi atau menghilangkan osilasi tekanan yang bermasalah.
Atenuasi pulsa tekanan dalam sistem pneumatik dapat dicapai melalui beberapa metode: ruang volume yang menyerap energi melalui kompresi gas, elemen restriktif yang menciptakan redaman melalui efek viskos, resonator yang disetel untuk membatalkan frekuensi tertentu, dan sistem pembatalan aktif yang menghasilkan pulsa balik. Peredaman yang efektif memerlukan pencocokan metode dengan konten frekuensi spesifik dan amplitudo fluktuasi tekanan.
Baru-baru ini saya bekerja dengan produsen peralatan pengemasan di Illinois yang sistem pneumatik berkecepatan tinggi mengalami fluktuasi tekanan yang parah yang menyebabkan kekuatan penyegelan yang tidak konsisten. Teknisi mereka telah mencoba tangki penerima dasar tanpa hasil. Melalui analisis denyut tekanan yang mendetail, kami mengidentifikasi bahwa sistem mereka memiliki beberapa komponen frekuensi yang membutuhkan pendekatan atenuasi yang berbeda. Dengan menerapkan solusi hibrida yang menggabungkan Resonator Helmholtz5 disetel ke osilasi 112 Hz yang dominan dan serangkaian lubang pembatasan, kami mengurangi fluktuasi tekanan sebesar 94% dan menghilangkan ketidakkonsistenan penyegelan sepenuhnya.
Mekanisme Atenuasi Fundamental
Beberapa mekanisme fisik dapat digunakan untuk melemahkan denyut tekanan:
Atenuasi Berbasis Volume
Bekerja melalui kompresibilitas gas:
- Menyediakan elemen kepatuhan yang menyerap energi tekanan
- Paling efektif untuk fluktuasi frekuensi rendah
- Implementasi sederhana dengan penurunan tekanan minimal
Atenuasi Berbasis Pembatasan
Bekerja melalui disipasi kental:
- Mengubah energi tekanan menjadi panas melalui gesekan
- Efektif di seluruh rentang frekuensi yang luas
- Menciptakan penurunan tekanan permanen
Atenuasi Berbasis Resonator
Bekerja melalui interferensi destruktif yang disetel:
- Membatalkan komponen frekuensi tertentu
- Sangat efektif untuk frekuensi yang ditargetkan
- Dampak minimal pada aliran kondisi mantap
Atenuasi Berbasis Material
Bekerja melalui kelenturan dan redaman dinding:
- Menyerap energi melalui deformasi dinding
- Menyediakan pelemahan broadband
- Dapat diintegrasikan ke dalam komponen yang sudah ada
Prinsip Desain Ruang Volume
Ruang volume (tangki penerima) adalah perangkat atenuasi yang paling umum:
Efektivitas ruang volume bergantung pada rasio volume ruang terhadap volume garis:
Rasio Atenuasi = 1 + (Vc/Vl)
Dimana:
- Vc = Volume ruang
- Vl = Volume garis
Untuk analisis yang bergantung pada frekuensi, rasio transmisinya adalah:
TR = 1/√(1 + (ωVc/Zc)²)
Dimana:
- ω = Frekuensi sudut (2πf)
- Zc = Impedansi karakteristik garis
Redaman Elemen Pembatas
Lubang, bahan berpori, dan lorong sempit yang panjang, menciptakan pelemahan melalui efek kental:
Penurunan tekanan melintasi batasan berikut ini:
ΔP = k(ρv²/2)
Dimana:
- k = Koefisien kerugian
- ρ = Kepadatan gas
- v = Kecepatan
Atenuasi yang diberikan meningkat seiring dengan:
- Kecepatan aliran yang lebih tinggi
- Panjang pembatasan yang lebih besar
- Diameter bagian yang lebih kecil
- Jalur aliran yang lebih berliku-liku
Sistem Atenuasi Resonator
Resonator yang disetel memberikan pelemahan frekuensi yang ditargetkan:
Resonator Helmholtz
Ruang volume dengan leher yang sempit, disetel ke frekuensi tertentu:
f = (c/2π)√(A/VL)
Dimana:
- f = Frekuensi resonansi
- c = Kecepatan suara
- A = Luas penampang leher
- V = Volume ruang
- L = Panjang leher efektif
Resonator Seperempat Gelombang
Tabung dengan panjang tertentu yang terbuka pada salah satu ujungnya:
f = c/4L
Dimana:
- L = Panjang tabung
Resonator Cabang Samping
Beberapa cabang yang disetel untuk konten frekuensi yang kompleks:
- Setiap cabang menargetkan frekuensi tertentu
- Dapat mengatasi beberapa harmonisa secara bersamaan
- Dampak minimal pada jalur aliran utama
Sistem Pembatalan Aktif
Sistem canggih yang menghasilkan pulsa balik:
Tahap Penginderaan
- Mendeteksi gelombang tekanan yang masuk
- Menganalisis konten frekuensi dan amplitudoTahap Pemrosesan
- Hitung sinyal pembatalan yang diperlukan
- Mempertimbangkan dinamika sistem dan penundaanTahap Aktuasi
- Menghasilkan gelombang tekanan balik
- Waktu yang tepat untuk gangguan yang merusak
Perbandingan Kinerja Atenuasi
| Metode | Frekuensi Rendah (<50 Hz) | Frekuensi Menengah (50-200 Hz) | Frekuensi Tinggi (>200 Hz) | Penurunan Tekanan | Kompleksitas |
|---|---|---|---|---|---|
| Ruang Volume | Luar biasa (>90%) | Sedang (40-70%) | Miskin (<30%) | Sangat Rendah | Rendah |
| Lubang Pembatas | Miskin (<30%) | Baik (60-80%) | Luar biasa (>80%) | Tinggi | Rendah |
| Resonator Helmholtz | Resonansi luar yang buruk | Sangat baik dalam resonansi | Resonansi luar yang buruk | Rendah | Sedang |
| Tabung Gelombang Seperempat | Resonansi luar yang buruk | Sangat baik dalam resonansi | Resonansi luar yang buruk | Rendah | Sedang |
| Beberapa Resonator | Sedang (40-60%) | Luar biasa (>80%) | Baik (60-80%) | Rendah | Tinggi |
| Pembatalan Aktif | Luar biasa (>90%) | Luar biasa (>90%) | Baik (70-85%) | Tidak ada | Sangat Tinggi |
| Sistem Hibrida | Luar biasa (>90%) | Luar biasa (>90%) | Luar biasa (>90%) | Sedang | Tinggi |
Implementasi Atenuasi Praktis
Untuk pelemahan denyut nadi tekanan yang efektif:
Mengkarakterisasi Fluktuasi
- Mengukur konten amplitudo dan frekuensi
- Mengidentifikasi frekuensi dominan
- Tentukan apakah broadband atau frekuensi tertentu memerlukan pelemahanPilih Metode yang Sesuai
- Untuk frekuensi rendah: Ruang volume
- Untuk frekuensi tertentu: Resonator yang disetel
- Untuk pelemahan broadband: Pembatasan atau pendekatan hibrida
- Untuk aplikasi penting: Pembatalan aktifOptimalkan Penempatan
- Dekat sumber untuk mencegah penyebaran
- Dekat komponen sensitif untuk melindunginya
- Di lokasi-lokasi strategis untuk memecah pola gelombang berdiriVerifikasi Kinerja
- Mengukur sebelum/sesudah atenuasi
- Konfirmasikan di seluruh kondisi pengoperasian
- Memastikan tidak ada konsekuensi yang tidak diinginkan
Studi Kasus: Pelemahan Multi-Metode dalam Pengemasan Berkecepatan Tinggi
Untuk sistem penyegelan pneumatik berkecepatan tinggi yang mengalami fluktuasi tekanan:
| Parameter | Sebelum Atenuasi | Setelah Ruang Volume | Setelah Solusi Hibrida | Peningkatan |
|---|---|---|---|---|
| Frekuensi Rendah (<50 Hz) | ± 0,8 bar | ± 0,12 bar | ± 0,05 bar | Pengurangan 94% |
| Frekuensi Menengah (112 Hz) | ± 1,2 bar | ± 0,85 bar | ± 0,07 bar | Pengurangan 94% |
| Frekuensi Tinggi (>200 Hz) | ± 0,4 bar | ± 0,36 bar | ± 0,04 bar | Pengurangan 90% |
| Variasi Kekuatan Segel | ±28% | ± 22% | ± 2.5% | Peningkatan 91% |
| Tingkat Penolakan Produk | 4.2% | 3.1% | 0.3% | Pengurangan 93% |
| Efisiensi Sistem | Baseline | +4% | +12% | Peningkatan 12% |
Studi kasus ini menunjukkan bagaimana pendekatan multi-metode yang ditargetkan untuk pelemahan dapat secara dramatis meningkatkan kinerja sistem.
Teknik Atenuasi Tingkat Lanjut
Untuk aplikasi yang sangat menantang:
Atenuasi Terdistribusi
Menggunakan beberapa perangkat yang lebih kecil daripada satu perangkat besar:
- Menempatkan atenuasi lebih dekat ke sumber dan komponen sensitif
- Memecah pola gelombang berdiri dengan lebih efektif
- Memberikan redundansi dan kinerja yang lebih konsisten
Peredaman Selektif Frekuensi
Menargetkan frekuensi tertentu yang bermasalah:
- Menggunakan beberapa resonator yang disetel ke frekuensi yang berbeda
- Mempertahankan respons sistem yang diinginkan sekaligus menghilangkan masalah
- Meminimalkan dampak pada kinerja sistem secara keseluruhan
Sistem Adaptif
Menyesuaikan atenuasi berdasarkan kondisi pengoperasian:
- Menggunakan sensor untuk memantau fluktuasi tekanan
- Menyesuaikan parameter atenuasi secara otomatis
- Mengoptimalkan kinerja di berbagai kondisi
Kesimpulan
Memahami teori fluktuasi tekanan-kecepatan perambatan gelombang, verifikasi gelombang berdiri, dan metode pelemahan pulsa-memberikan fondasi untuk desain sistem pneumatik yang andal dan efisien. Dengan menerapkan prinsip-prinsip ini, Anda dapat menghilangkan masalah kinerja yang misterius, memperpanjang usia komponen, dan meningkatkan efisiensi sistem sekaligus memastikan pengoperasian yang konsisten di semua kondisi pengoperasian.
Tanya Jawab Tentang Fluktuasi Tekanan dalam Sistem Pneumatik
Bagaimana fluktuasi tekanan memengaruhi masa pakai komponen pneumatik?
Fluktuasi tekanan secara signifikan mengurangi masa pakai komponen melalui beberapa mekanisme: menyebabkan keausan seal yang dipercepat dengan menciptakan gerakan mikro pada permukaan penyegelan; menyebabkan kelelahan material pada diafragma dan elemen fleksibel melalui siklus tegangan berulang; meningkatkan pelonggaran sambungan ulir melalui getaran; dan menciptakan konsentrasi tegangan lokal pada transisi geometris. Sistem dengan fluktuasi tekanan yang tidak terkendali yang parah biasanya mengalami masa pakai komponen 40-70% lebih pendek dibandingkan dengan sistem yang teredam dengan baik, dengan seal dan diafragma yang sangat rentan.
Apa hubungan antara panjang saluran dan waktu respons tekanan dalam sistem pneumatik?
Panjang saluran secara langsung memengaruhi waktu respons tekanan dengan mengikuti hubungan sederhana: waktu respons meningkat secara linier dengan panjang saluran pada tingkat yang ditentukan oleh kecepatan rambat gelombang. Untuk udara pada kondisi standar (kecepatan gelombang ≈ 343 m/s), setiap meter saluran menambahkan sekitar 2,9 milidetik penundaan transmisi. Namun, waktu penumpukan tekanan yang sebenarnya biasanya 2-5 kali lebih lama daripada waktu transmisi gelombang awal karena perlunya beberapa pantulan untuk menyamakan tekanan. Ini berarti saluran 5 meter mungkin memiliki waktu transmisi gelombang 14,5 ms tetapi waktu penumpukan tekanan 30-70 ms.
Bagaimana cara mengidentifikasi jika sistem pneumatik saya mengalami fluktuasi tekanan resonansi?
Fluktuasi tekanan resonansi biasanya termanifestasi melalui beberapa gejala yang dapat diamati: komponen bergetar pada frekuensi operasi tertentu tetapi tidak pada frekuensi operasi lainnya; kinerja sistem bervariasi secara tidak konsisten dengan perubahan kecil pada kondisi operasi; terdengar suara "nyanyian" atau "siulan" dari saluran pneumatik; alat pengukur tekanan menunjukkan pembacaan yang berosilasi; dan kinerja aktuator (kecepatan, gaya) bervariasi secara siklis. Untuk mengonfirmasi resonansi, ukur tekanan di berbagai titik dalam sistem menggunakan transduser respons cepat (waktu respons <1ms) dan cari pola gelombang berdiri di mana amplitudo tekanan bervariasi dengan posisi di sepanjang garis.
Apakah fluktuasi tekanan memengaruhi efisiensi energi dalam sistem pneumatik?
Fluktuasi tekanan secara signifikan berdampak pada efisiensi energi, biasanya menguranginya sebesar 10-25% melalui beberapa mekanisme: fluktuasi tekanan meningkatkan tingkat kebocoran dengan menciptakan tekanan puncak yang lebih tinggi; fluktuasi tekanan memboroskan energi dalam kompresi dan ekspansi siklus; fluktuasi tekanan menyebabkan peningkatan gesekan pada komponen karena getaran; dan fluktuasi tekanan sering kali membuat operator meningkatkan tekanan suplai untuk mengimbangi masalah kinerja. Selain itu, turbulensi dan pemisahan aliran yang disebabkan oleh fluktuasi tekanan mengubah energi tekanan yang berguna menjadi panas buangan. Meredam fluktuasi tekanan dengan benar dapat meningkatkan efisiensi sistem sebesar 5-15% tanpa perubahan lain.
Bagaimana perubahan suhu memengaruhi perilaku gelombang tekanan dalam sistem pneumatik?
Suhu secara signifikan memengaruhi perilaku gelombang tekanan melalui beberapa mekanisme: suhu secara langsung memengaruhi kecepatan rambat gelombang (sekitar +0,6 m/s per kenaikan suhu °C); suhu mengubah kerapatan dan viskositas gas, sehingga mengubah karakteristik redaman; suhu memodifikasi sifat elastis saluran pneumatik, yang memengaruhi pantulan dan transmisi gelombang; serta suhu menggeser frekuensi resonansi (sekitar +0,17% per °C). Sensitivitas suhu ini berarti sistem yang beroperasi dengan sempurna pada suhu 20°C mungkin mengalami resonansi yang bermasalah saat beroperasi pada suhu 40°C, atau perangkat redaman yang disetel untuk kondisi musim dingin mungkin tidak efektif selama musim panas.
-
Memberikan penjelasan rinci tentang fisika di balik kecepatan suara, cara penghitungannya, dan faktor-faktor yang mempengaruhinya. ↩
-
Menawarkan pemahaman dasar tentang fenomena gelombang berdiri, termasuk bagaimana gelombang tersebut terbentuk dari interferensi dan karakteristik utamanya seperti node dan antinode. ↩
-
Memberikan bukti dan studi industri yang memverifikasi kisaran umum kehilangan energi yang disebabkan oleh ketidakefisienan seperti fluktuasi tekanan dalam sistem pneumatik. ↩
-
Menjelaskan komponen dan fungsi Unit Persiapan Udara (FRL), yang sangat penting untuk menjaga kualitas udara dalam sistem pneumatik. ↩
-
Menawarkan penjelasan mendalam tentang prinsip-prinsip di balik resonator Helmholtz, perangkat penting untuk pelemahan frekuensi yang ditargetkan dalam sistem akustik dan fluida. ↩



