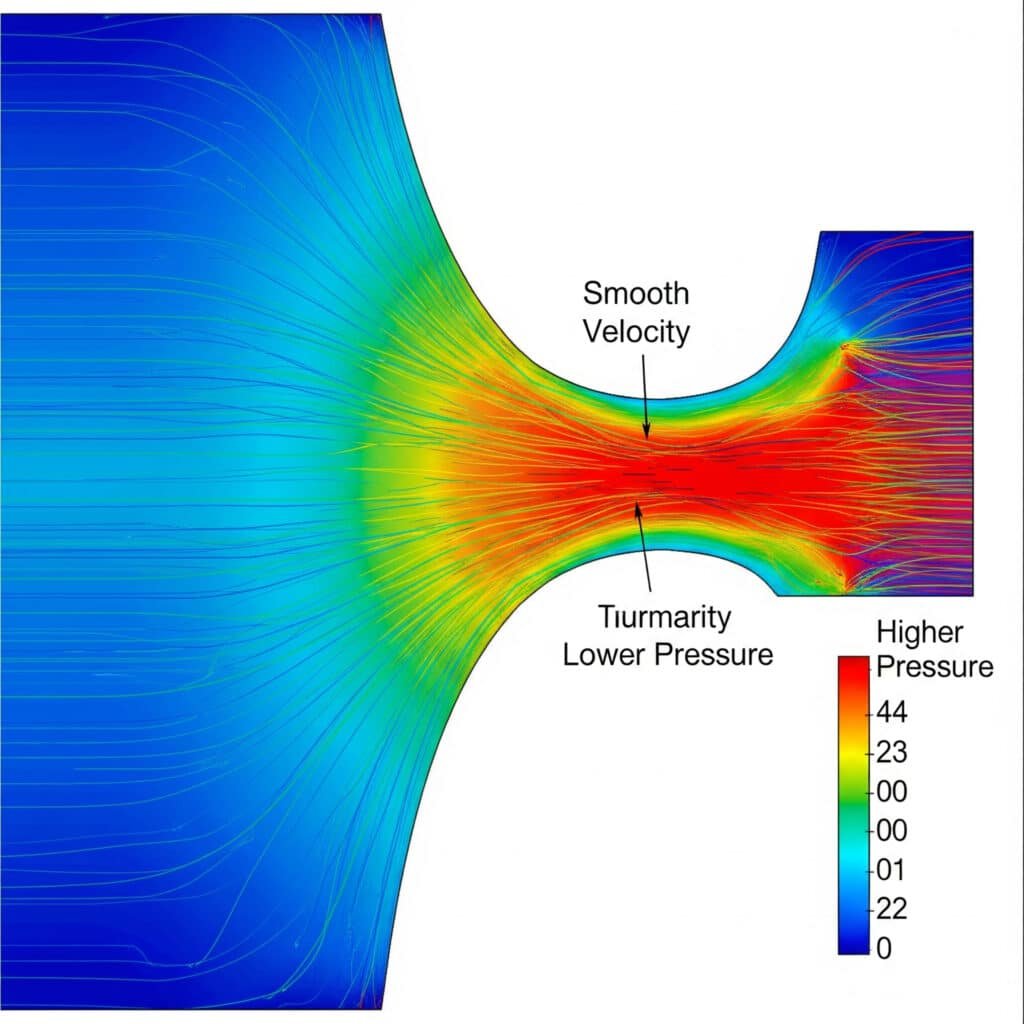
気体流の問題は、エネルギーの浪費やシステムの故障によって、メーカーに毎年何十億もの損失を与えている。エンジニアはしばしば液体流の原理をガスシステムに適用し、致命的な誤算を引き起こします。ガス流の原理を理解することで、コストのかかる設計ミスや安全上の危険を防ぐことができます。
気体流の原理は、連続の方程式、運動量保存、エネルギー保存によって支配される。 圧縮性流れ1 方程式は、非圧縮性の液体の流れとは根本的に異なる。
年前、私はサラ・トンプソンという英国の化学エンジニアと仕事をした。彼女のチームは、圧縮性ガスの流れに対して非圧縮性の流れ計算を使っていました。適切なガス流の原理を導入した後、圧力サージをなくし、エネルギー消費を35%削減しました。
目次
- ガスの流れを支配する基本原理とは?
- 圧縮性流れ方程式は液体流れとどう違うのか?
- 産業システムにおけるガス流挙動に影響を与える要因とは?
- 気体の流れにおける圧力、温度、速度の相互作用とは?
- さまざまなガス・フロー・レジームとは?
- 産業用途におけるガス流量の計算と最適化方法とは?
- 結論
- ガスフロー原理に関するFAQ
ガスの流れを支配する基本原理とは?
気体の流れは、すべての流体運動を支配する3つの基本的な保存則のもとで作動するが、気体の圧縮性と密度の変化による独特の性質がある。
気体流の原理は、質量保存則(連続の式)、運動量保存則(ニュートンの第二法則)、エネルギー保存則(熱力学の第一法則)に基づいており、圧縮性流体の挙動に合わせて修正されている。
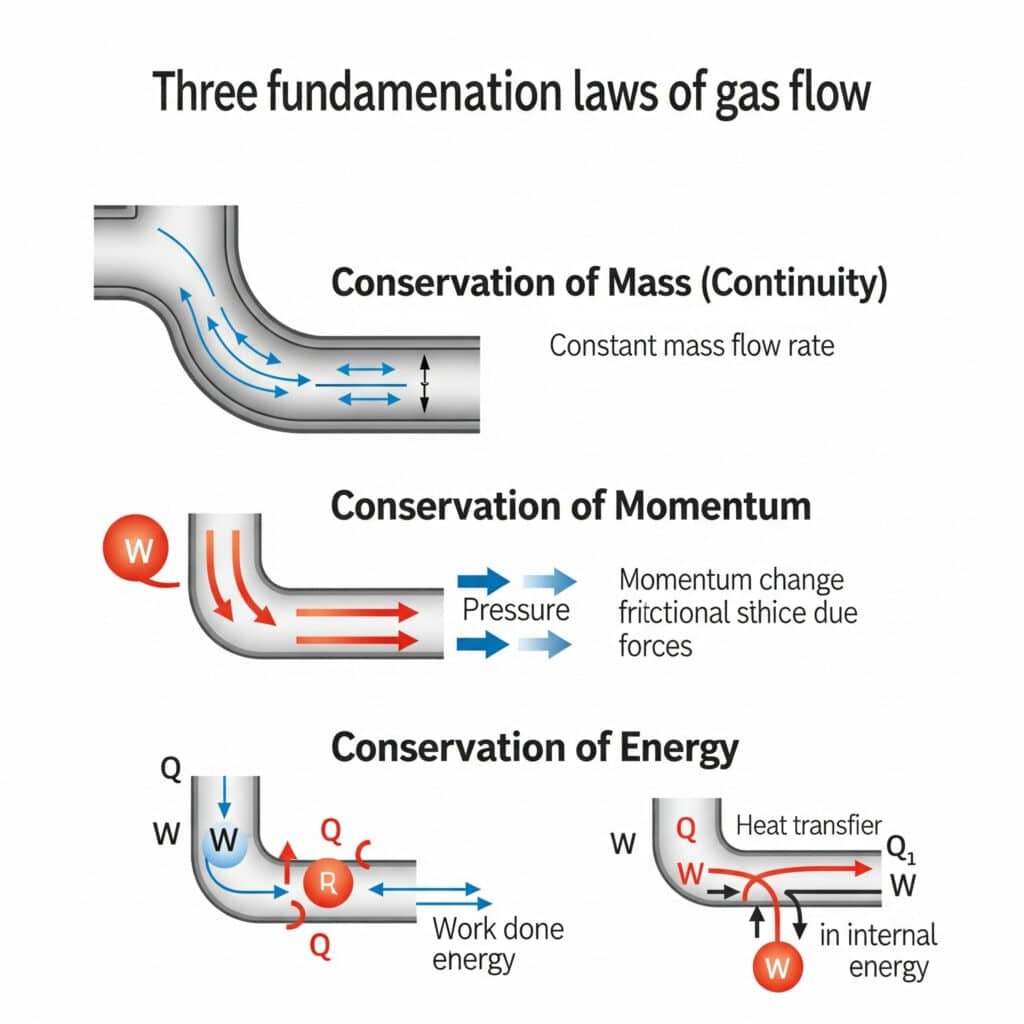
質量保存(連続方程式)
気体流の連続方程式は、非圧縮性液体とは異なり、圧力と温度の変化によって生じる密度の変化を考慮する。
ガス流の連続方程式:
∂t + ρ/∇-(ρ_2V) = 0
安定した流れのために: ρ₁A₁V₁ = ρ₂A₂V₂
どこでだ:
- ρ = 気体密度(圧力と温度によって変化する)
- A = 断面積
- V = ガス速度
- t = 時間
重要な意味合い
- 気体の密度は圧力と温度によって変化する
- 定常流では質量流量は一定
- 密度が小さくなるにつれて速度は増加する
- 面積の変化は速度と密度の両方に影響する
運動量保存
気体流における運動量保存は、圧縮性流体に作用する圧力力、粘性力、体力を考慮する。
運動量方程式ナビエ・ストークス2):
ρ(∂V/∂t + V-∇V) = -∇p + μ∇²V + ρg
ガスフロー用:
- 高速流では圧力勾配項が支配的
- 壁際や層流で重要な粘性効果
- 圧縮性の影響はマッハ0.3以上で顕著になる。
エネルギー保存
気体流のエネルギー保存には、運動エネルギー、位置エネルギー、内部エネルギー、および圧縮と膨張による温度変化を考慮した流れの仕事が含まれる。
エネルギー方程式:
h + V²/2 + gz = 定数 (流線に沿って)
どこでだ:
- h = 比エンタルピー(内部エネルギーと流れの仕事を含む)
- V²/2 = 単位質量当たりの運動エネルギー
- gz = 単位質量当たりの位置エネルギー
エネルギーへの配慮:
| エネルギー形態 | ガスフローへの影響 | 典型的なマグニチュード |
|---|---|---|
| 運動エネルギー | 高速で顕著 | V²/2 |
| 圧力エネルギー | ほとんどの用途で優勢 | p/ρ |
| 内部エネルギー | 温度による変化 | Cm_1D65 |
| フロー・ワーク | ガス移動に必要 | pv |
状態方程式
気体の流れには、圧力、密度、温度を関係づける状態方程式が必要であり、ほとんどの工業用途では理想気体の法則が一般的である。
理想気体の法則:
p = ρRT
どこでだ:
- p = 絶対圧
- ρ = 気体密度
- R = 比気体定数
- T = 絶対温度
実際の気体では、ファンデルワールス方程式やレドリック・クウォン方程式など、より複雑な状態方程式が必要になることもある。
圧縮性流れ方程式は液体流れとどう違うのか?
圧縮性気体流は、非圧縮性液体流とは基本的に異なる挙動を示すため、特殊な解析手法や設計上の配慮が必要となります。
圧縮性流れは、密度の変化、音速の制限、衝撃波の形成、非圧縮性液体流体系では発生しない温度と圧力のカップリングによって異なる。
密度変動の影響
ガス密度は圧力と温度によって大きく変化し、流れのパターン、流速分布、システム設計要件に影響を与えます。
密度変化の影響:
- 速度 加速度:気体は膨張すると加速する
- 圧力降下:非線形の圧力と流れの関係
- 温度効果:密度は温度に反比例する
- チョークド・フロー:最大流量の制限
音速とマッハ数
気体の流動挙動は、流速が音速に近づくにつれて劇的に変化するため、液体システムにはない重要な設計上の制約が生じる。
音速計算:
a = √(γRT)
どこでだ:
- a = 気体の音速
- γ=比熱比(Cp/Cv)
- R = 比気体定数
- T = 絶対温度
マッハ数3 意義がある:
M = V/a (音速に対する速度比)
| マッハレンジ | フロー・レジーム | 特徴 |
|---|---|---|
| M < 0.3 | 非圧縮性 | 密度は基本的に一定 |
| 0.3 < M < 1.0 | 亜音速圧縮性 | 密度の大幅な変化 |
| M = 1.0 | ソニック | 臨界流量条件 |
| M > 1.0 | スーパーソニック | 衝撃波の可能性 |
チョークド・フロー現象
チョークド・フロー4 ガス速度が音速状態に達すると発生し、下流の圧力低下に関係なく最大流量が制限される。
チョークド・フローの状態:
- 達成された最大質量流量
- 下流の圧力変化は上流の流量に影響しない
- 臨界圧力比:空気の場合、p₂/p₁≒0.53
- ノズル、オリフィス、コントロールバルブに一般的
温度-圧力カップリング
ガスの流れは、膨張と圧縮による大きな温度変化を伴い、システムの性能と設計に影響を与える。
熱力学的プロセス:
- 等方流:可逆的な断熱プロセス
- 等温流:一定温度(熱伝達を伴う緩やかな流れ)
- 断熱フロー:熱伝導なし(急流)
- ポリトロピック・フロー:熱移動を伴う一般的なケース
産業システムにおけるガス流挙動に影響を与える要因とは?
工業用途のガス流挙動には複数の要因が影響するため、適切なシステム設計と運用のためには包括的な分析が必要です。
主な要因には、ガス特性、システム形状、運転条件、伝熱効果、壁面摩擦などがあり、これらによってフローパターン、圧力損失、システム性能が総合的に決定される。
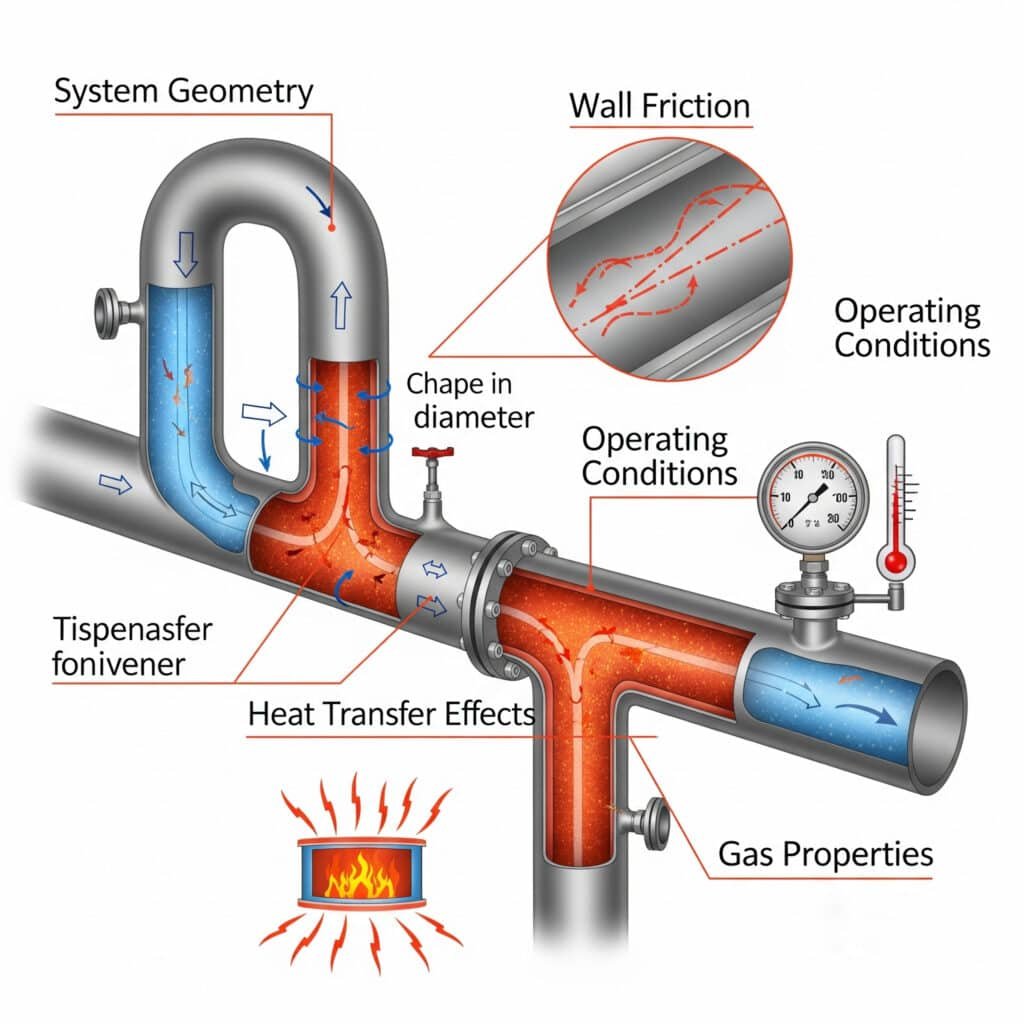
ガス特性への影響
さまざまなガスは、その分子特性、比熱比、熱力学的挙動に基づいて、さまざまな流動特性を示す。
臨界ガス特性:
| プロパティ | シンボル | フローへの影響 | 代表値 |
|---|---|---|---|
| 比熱比 | γ | 音速、膨張 | 1.4 (空気), 1.3 (CO₂) |
| ガス定数 | R | 密度-圧力の関係 | 287 J/kg・K(空気) |
| 粘度 | μ | 摩擦損失 | 1.8×10-⁵ Pa・s(空気) |
| 分子量 | M | ある条件下での密度 | 29 kg/kmol(空気) |
システム・ジオメトリー効果
パイプの直径、長さ、継手、流路面積の変化は、ガスの流れパターンと圧力損失に大きく影響する。
ジオメトリーに関する考察:
- パイプ径:速度と摩擦損失に影響
- 長さ:総摩擦圧損を決定する
- エリア変更:加減速エフェクトの作成
- 付属品:局所的な圧力損失を引き起こす
- 表面粗さ:摩擦係数に影響
使用圧力と温度
システムの運転条件は、熱力学的な関係を通じて、ガス密度、粘度、流動挙動に直接影響する。
動作条件の影響:
- 高圧:密度を高め、圧縮性の影響を減らす
- 低圧:密度を下げ、速度を上げる
- 高温:密度を下げ、音速を上げる
- 低温:密度が高くなり、結露の原因となる。
伝熱効果
ガス流動中の熱の付加や除去は、温度、密度、圧力分布に大きく影響する。
熱伝達のシナリオ:
- 暖房:温度上昇、密度低下、流動促進
- 冷却:温度低下、密度上昇、流れ減速
- 断熱:熱伝導なし、膨張・圧縮による温度変化
- 等温:熱伝導によって維持される一定温度
壁面摩擦の影響
ガスとパイプ壁の間の摩擦は圧力損失を生み、特に長いパイプラインで重要な速度プロファイルに影響を与える。
摩擦損失の計算:
Δp = f × (L/D) × (ρV²/2)
どこでだ:
- f = 摩擦係数(レイノルズ数と粗さの関数)
- L = パイプの長さ
- D = パイプの直径
- ρ = 気体密度
- V = ガス速度
気体の流れにおける圧力、温度、速度の相互作用とは?
ガス流における圧力、温度、流速の相互作用は複雑な関係を生み、適切なシステム設計と解析のために理解されなければならない。
気体流の相互作用は、圧力の変化が温度と密度に影響し、流速の変化が運動量効果を通じて圧力に影響し、温度の変化が状態方程式を通じて他のすべての特性に影響するという熱力学的関係に従う。
圧力と速度の関係
気体の速度と圧力は、圧縮性流体用に修正されたベルヌーイの方程式によって反比例の関係にあり、設計上のユニークな課題を生み出している。
気体の流れに対する修正ベルヌーイ方程式:
∫dp/ρ + V²/2 + gz = 定数
理想気体の場合: γ/(γ-1) × (p/ρ) + V²/2 = 定数
圧力と速度の効果:
- 圧力降下:ガス膨張による速度上昇
- 速度向上:運動量効果により、さらなる圧力低下を引き起こす可能性がある
- 加速:ガスがシステム内で膨張する際に自然に発生する
- 減速:増圧または面積拡大が必要
温度-速度カップリング
気体の温度と流速はエネルギー保存を通じて連動しており、温度の変化は気体の特性と流れの挙動に影響を与える。
温度と速度の関係:
T₀ = T + V²/(2Cp)
どこでだ:
- T₀ = 停滞(全)温度
- T = 静的温度
- V = ガス速度
- Cp = 一定圧力における比熱
実践的な意味合い:
- 高速ガスフローが静的温度を下げる
- 断熱流れでは停滞温度は一定に保たれる
- 温度変化は気体の密度と粘度に影響を与える
- 冷却は、ガスによっては凝縮を引き起こす可能性がある。
圧力-温度効果
圧力と温度は、状態方程式と熱力学的過程を通じて相互作用し、気体の密度と流動特性に影響を与える。
熱力学的プロセス関係:
| プロセスタイプ | 圧力と温度の関係 | 申し込み |
|---|---|---|
| 等方性 | p/p ₀ = (T/T ₀)^(γ/(γ-1)) | ノズル、ディフューザー |
| 等温 | pV = 一定、T = 一定 | 熱伝達を伴う低速流 |
| アイソバリック | p = 定数 | 定圧加熱 |
| アイソコリック | V = 一定 | 定容量加熱 |
密度の変化
気体密度は理想気体の法則に従って圧力と温度の両方で変化し、複雑な流動挙動を生み出す。
密度の計算:
ρ = p/(RT)
密度によるフローへの影響:
- 高密度:与えられた質量流量に対してより低い流速
- 低密度:より高い速度、潜在的な圧縮性の影響
- 密度勾配:浮力と混合効果を生み出す
- 密度の変化:運動量とエネルギー移動に影響
私は最近、テキサス州のロバート・チェンというアメリカの天然ガス・エンジニアのパイプライン・システムの最適化を手伝った。温度-圧力-速度の相互作用を適切に考慮することで、処理能力を15%増加させながら、ポンプエネルギーを28%削減しました。
さまざまなガス・フロー・レジームとは?
ガス流は、流速、圧力条件、システム形状によって異なるレジームを示し、それぞれに特有の解析手法と設計上の考慮事項が必要となる。
気体の流れには、層流、乱流、亜音速流、音速流、超音速流があり、それぞれ異なる流速分布、圧力関係、熱伝達特性を特徴とする。
層流と乱流
気体の流れは、層流から乱流へと変化する。 レイノルズ数5圧力損失、熱伝達、混合特性に影響を与える。
気体流のレイノルズ数:
Re = ρVD/μ
どこでだ:
- ρ = 気体密度(圧力と温度によって変化する)
- V = 平均速度
- D = パイプの直径
- μ = 動粘度
流況の分類:
| レイノルズ数 | フロー・レジーム | 特徴 |
|---|---|---|
| Re < 2300 | 層流 | スムーズで予測可能な流れ |
| 2300 < Re < 4000 | トランジション | 不安定な混合行動 |
| Re > 4000 | 乱気流 | カオス的な強化ミキシング |
亜音速流領域
亜音速流は、気体速度が局所的な音速よりも小さいときに発生し、圧力擾乱を上流に伝播させる。
亜音速流の特性:
- マッハ数:M < 1.0
- 圧力伝播:乱れは上流へ
- フロー制御:下流の状況はシステム全体に影響する
- 密度の変化:中程度、予測可能な変動
- デザインの柔軟性:複数のソリューションが可能
亜音速流の応用:
- ほとんどの産業用ガス供給システム
- HVACおよび換気システム
- 低圧空気圧システム
- 化学プロセス装置
- 発電所ガス処理
ソニック・フロー(チョークド・フロー)
音速流は、気体速度が局所的な音速に等しいときに発生し、独特の特性を持つ臨界流状態を作り出す。
音波フロー特性:
- マッハ数:M = 1.0ちょうど
- 最大マスフロー:超過不可
- プレッシャーの独立性:下流圧力は流量に影響しない
- 臨界圧力比:通常、空気は約0.53
- 温度効果:大幅な温度低下
ソニックフローの応用:
- ガスタービン用ノズル
- セーフティリリーフバルブ
- 流量測定装置
- ロケットエンジンのノズル
- 高圧ガスレギュレーター
超音速流領域
超音速流は、気体の流速が音速を超えるときに発生し、衝撃波や独特の流動現象を引き起こす。
超音速流の特性:
- マッハ数:M > 1.0
- 衝撃波:急激な圧力と温度の変化
- 流れ方向:情報は上流には行けない
- 拡張波:スムーズな減圧
- デザインの複雑さ:専門的な分析が必要
衝撃波の種類
| ショックタイプ | 特徴 | アプリケーション |
|---|---|---|
| 通常のショック | 流れに対して垂直 | ディフューザー、インレット |
| 斜めの衝撃 | 流れ方向に対して角度をつける | 超音速機 |
| 拡張ファン | 徐々に圧力を下げる | ノズルデザイン |
極超音速流
極超音速流は非常に高いマッハ数(通常、M > 5)で発生し、そこではさらなる効果が重要になる。
極超音速効果:
- リアルガス効果:理想気体の法則が崩れる
- 化学反応:解離とイオン化
- 熱伝達:極端な加熱効果
- 粘性効果:境界層相互作用
産業用途におけるガス流量の計算と最適化方法とは?
ガス流量の計算には、圧縮性の影響を考慮した特殊な方法が必要であり、最適化はエネルギー消費量の最小化とシステム性能の最大化に重点を置く。
ガス流の計算には、圧縮性流体方程式、摩擦係数の相関関係、熱力学的関係が使用され、最適化には、エネルギーコストを最小化するための配管サイズ決定、圧力レベルの選択、システム構成が含まれる。
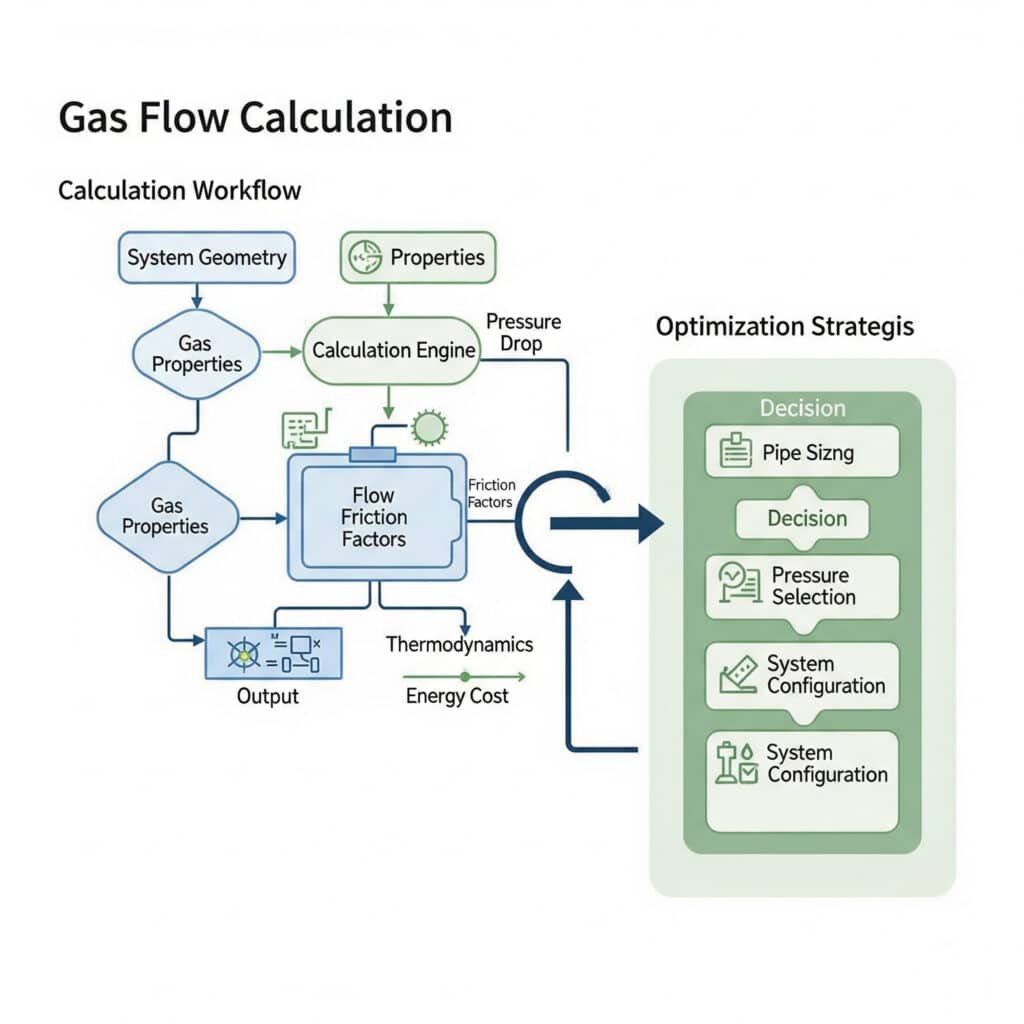
基本的なガス流量計算
気体の流れの計算は、圧縮性の流れの影響と実際の気体の特性を考慮して修正された基本方程式から始まります。
質量流量の計算:
ṁ = ρAV = (p/RT)AV
オリフィスを通るチョークドフロー用:
ṁ = CdA√(γρp)[2/(γ+1)]^((γ+1)/(2(γ-1)))
どこでだ:
- Cd = 放電係数
- A = オリフィス面積
- γ = 比熱比
- ρ = 上流密度
- p = 上流圧力
圧力損失の計算
ガス流の圧力損失計算は、摩擦損失に加えて、ガス膨張による加速効果を考慮する必要があります。
総圧力損失コンポーネント:
- 摩擦圧力降下:壁のせん断応力によるもの
- 加速圧力降下:速度上昇のため
- 標高圧力降下:重力効果によるもの
- フィッティング圧力降下:流れの乱れによるもの
摩擦圧損の計算式:
Δpf = f(L/D)(ρV²/2)
加速圧力降下:
Δpa = ρ₂V₂² - ρ₁V₁² (エリア変更の場合)
パイプラインフロー分析
長いパイプラインの解析では、パイプラインの長さに沿ってガス特性が変化するため、繰り返し計算が必要になります。
パイプラインの計算ステップ:
- ディバイド・パイプライン:一定の特性を持つセグメントへ
- セグメント・プロパティの計算:圧力、温度、密度
- フローレジームの決定:層流または乱流
- 圧力損失の計算:各セグメント
- プロパティの更新:次のセグメントへ
- 繰り返し:収束するまで
簡易パイプライン方程式:
p₁² - p₂² = (fL_1E41↩²RT)/(A²Dρ₀)
どこでだ:
- p₁、p₂=入口圧力と出口圧力
- f = 平均摩擦係数
- L = パイプラインの長さ
- ↪Ll_1 = 質量流量
- R = 気体定数
- T = 平均気温
- A = パイプ面積
- D = パイプの直径
- ρ ₀ = 基準密度
システム最適化戦略
ガス・フロー・システムの最適化は、最小のライフサイクル・コストを達成するために、資本コスト、運転コスト、性能要件のバランスをとる。
最適化パラメータ:
| パラメータ | システムへの影響 | 最適化戦略 |
|---|---|---|
| パイプ径 | 資本コスト対圧力損失 | 経済直径計算 |
| 動作圧力 | 圧縮コスト対パイプコスト | 圧力レベルの最適化 |
| コンプレッサー・ステージング | 効率と複雑さの比較 | ステージ番号の最適化 |
| 熱交換器のサイズ | 熱回収対資本コスト | 経済的な熱交換 |
経済的なパイプサイジング
経済的な配管サイズ決定は、配管資本コストとポンプ・エネルギー・コストのバランスをシステム寿命にわたってとる。
経済直径の計算式:
D_economic = K(ṁ/ρ)^0.37
Kはどこに依存するか:
- エネルギーコスト
- パイプコスト
- システム寿命
- 金利
- 年間稼働時間
流量測定と制御
正確なガス流の測定と制御には、測定装置に対する圧縮性の流れの影響を理解する必要があります。
流量測定に関する考察:
- オリフィスプレート:圧縮率補正が必要
- ベンチュリーメーター:圧縮性の影響を受けにくい
- タービン・メーター:ガス密度変化の影響を受ける
- 超音波計:温度補正が必要
- コリオリメーター:直接質量流量測定
数値流体力学(CFD)
複雑なガス流システムは、CFD解析によって性能を最適化し、さまざまな運転条件下での挙動を予測することができます。
CFDアプリケーション:
- 複雑な幾何学:不規則な形状と金具
- 熱伝達:流動と熱の複合解析
- 混合分析:ガス組成の変化
- 最適化:設計パラメータ研究
- トラブルシューティング:フローの問題を特定する
私は最近、アルバータ州のデビッド・ウィルソンというカナダの石油化学エンジニアと仕事をしました。彼のガス処理プラントは効率性の問題を抱えていました。CFD解析と適切なガス流計算を組み合わせ、20%のエネルギー浪費を引き起こしている再循環ゾーンを特定しました。設計変更を実施した結果、処理能力を向上させながら、エネルギー消費は18%減少しました。
結論
気体流の原理は、密度変化に対して修正された保存則によって圧縮性流体の挙動を支配するため、液体流体系とは根本的に異なる圧力-温度-速度の相互作用と圧縮性の効果を考慮した特殊な解析手法が必要となる。
ガスフロー原理に関するFAQ
ガス流の基本原理は何ですか?
気体の流れは、質量、運動量、エネルギーの保存則に基づいており、気体の密度が圧力と温度によって変化し、速度-圧力-温度の相互作用が生じる圧縮性流体の挙動に合わせて修正されている。
気体の流れと液体の流れはどう違うのですか?
気体の流れには、非圧縮性の液体流体系では起こらないような大きな密度変化、音速の制限、温度と圧力の連成、チョークドフロー現象などがある。
ガスシステムにおけるチョークドフローとは?
チョークドフローは、ガス流速が音速条件(マッハ=1.0)に達すると発生し、下流の圧力低下に関係なく最大質量流量が制限されるもので、ノズルやコントロールバルブでよく発生する。
ガス流量はどのように計算するのですか?
ガス流量の計算には、理想気体の法則に従って密度が圧力と温度によって変化する方程式ṁ = ρAVを使用するため、複雑なシステムでは反復解法が必要となる。
ガス流の挙動に影響を与える要因は何ですか?
主な要因には、ガス特性(分子量、比熱比)、システム形状(パイプ径、継手)、運転条件(圧力、温度)、熱伝達効果などがある。
気体の流れでマッハ数が重要なのはなぜですか?
マッハ数(流速/音速)は、亜音速流(M1)は衝撃波を発生させる。
-
流体の密度が圧力によって大きく変化する圧縮性流れと、密度が一定と仮定される非圧縮性流れの基本的な違いを説明。 ↩
-
運動量保存に基づいて粘性流体の運動を記述する、流体力学の基礎となる偏微分方程式群であるナビエ・ストークス方程式の概要を解説。 ↩
-
マッハ数とは、流体力学において、境界を通過する流速と局所的な音速の比を表す無次元量であり、流れのレジームを分類するために使用される。 ↩
-
チョークドフローとは、圧縮性流れにおける限界条件の一つで、最狭部の流速が音速に達し、下流側の圧力がさらに低下しても質量流量が増加しない現象のこと。 ↩
-
レイノルズ数とは、流れのパターンを予測するために使用される流体力学において重要な無次元量であり、層流(滑らかな流れ)と乱流(混沌とした流れ)を区別するのに役立ちます。 ↩


