
空気圧ラインに不思議な振動があることに気づいたことはありませんか?あるいは、供給圧力が安定しているにもかかわらず、シリンダーに原因不明の力の変動が発生していませんか?これらの現象はランダムではなく、圧力波がシステム内を伝播した結果であり、軽微な非効率から致命的な故障まで、さまざまな影響を引き起こします。
空気圧システムにおける圧力変動は、以下の速度で伝播する波動現象である。 音速1レゾナンスを含むダイナミックな効果を生み出す、 ていじょうは2そして圧力の増幅である。これらの変動は、コンポーネントの疲労や制御の不安定性を引き起こしかねないため、これらの変動を理解することは極めて重要である。 典型的な産業システムにおける10-25%のエネルギー損失3.
先月、私はテネシー州にある自動車組立工場のコンサルティングを行った。そこでは、重要な空圧クランプ・システムが、供給圧力が安定しているにもかかわらず、断続的な力の変動に見舞われていた。この工場のメンテナンスチームは、バルブやレギュレーターを交換し、さらにはシステム全体を交換した。 調気ユニット4 が成功しなかった。圧力波のダイナミクス、特に供給ラインの定在波パターンを分析することで、シリンダーで破壊的干渉を引き起こす周波数で動作していることを突き止めた。ラインの長さを調整するだけで、この問題は解消され、数週間の生産遅れを防ぐことができました。圧力変動理論を理解することで、空気圧システムの信頼性がどのように変わるかをお見せしましょう。
目次
- 波の伝播速度:圧力擾乱はシステム内をどのくらいの速度で伝播するか?
- 定在波の検証:共振周波数はどのように性能問題を引き起こすのか?
- パルス減衰法:破壊的な圧力振動を効果的に減衰させる技術とは?
- 結論
- 空気圧システムの圧力変動に関するFAQ
波の伝播速度:圧力擾乱はシステム内をどのくらいの速度で伝播するか?
圧力外乱が空気圧システム内を伝播する速度を理解することは、その影響を予測し制御するための基本です。伝播速度は、システムの応答時間、共振周波数、破壊的干渉の可能性を決定します。
ここで、γは比熱比、Rは比ガス定数、Tは絶対温度である。20℃の空気の場合、これは約343m/sに相当するが、この速度はパイプの弾性、ガスの圧縮性、流動条件などの要因によって変化する。
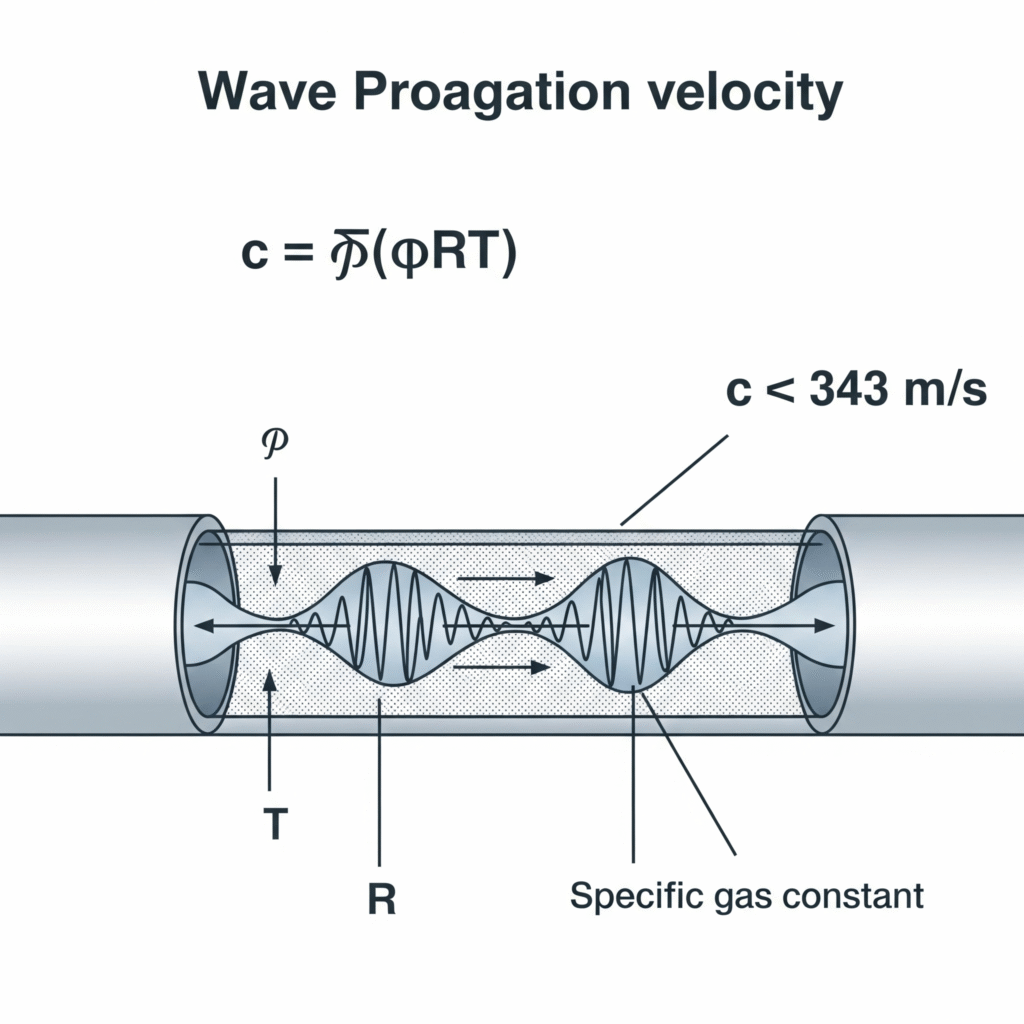
私は最近、スイスの精密組立機械のトラブルシューティングを手伝った。そこでは、空気圧グリッパーが作動してから力を加えるまでに12ミリ秒の遅れが生じていた。同社のエンジニアは、圧力伝達が瞬時に行われると思い込んでいたのです。システム内の実際の波動伝播速度(328m/s)を測定し、4mのライン長を考慮することで、理論的な伝播時間を12.2msと計算しました。バルブの位置をアクチュエーターに近づけると、この遅延は3msに短縮され、生産量は14%増加した。
基本波速度方程式
気体中の圧力波の伝播速度の基本式は次の通りである:
c = √(γRT)
どこでだ:
- c = 波の伝播速度(m/s)
- γ=比熱比(空気の場合は1.4)
- R = 比気体定数(空気の場合、287 J/kg-K)
- T = 絶対温度(K)
20℃(293K)の空気の場合、これは次のようになる:
c = √(1.4 × 287 × 293) = 343 m/s
空気圧ラインにおける修正波速度
実際の空気圧システムでは、実効波速度はパイプの弾性およびその他の要因によって式に従って修正される:
c_eff = c / √(1 + (Dψ/Eh))
どこでだ:
- c_eff = 有効波速度 (m/s)
- D = パイプの直径 (m)
- ψ = ガス圧縮係数
- E = パイプ材料の弾性係数 (Pa)
- h = パイプの肉厚 (m)
波速に対する温度と圧力の影響
波速は運転条件によって変化する:
| 温度 | 圧力 | 空気中の波速度 | 実践的な意味合い |
|---|---|---|---|
| 0°C (273K) | 1バー | 331 m/s | 寒い環境では反応が鈍くなる |
| 20°C (293K) | 1バー | 343 m/s | 基準条件 |
| 40°C (313K) | 1バー | 355 m/s | 温暖な環境での反応が速い |
| 20°C (293K) | 6バー | 343 m/s* | 圧力が速度に直接及ぼす影響はほとんどない |
*注:基本波速度は圧力に依存しないが、実際のシステムにおける実効波速度は、圧力に起因するパイプの弾性とガスの挙動の変化によって影響を受ける可能性がある。
実用的な波動伝播時間の計算
空気圧システムの場合:
- ラインの長さ(L):5メートル
- 使用温度:20℃(c = 343 m/s)
- パイプの材質ポリウレタン管(流速を約5%変化させる)
実効波速度はこうなる:
c_eff = 343 × 0.95 = 326 m/s
そして、波の伝播時間は次のようになる:
t = L/c_eff = 5/326 = 0.0153秒(15.3ミリ秒)
これは、圧力変化がラインの一方の端からもう一方の端まで移動するのに必要な最小時間を表しており、高速アプリケーションでは重要な要素です。
波速測定技術
空気圧システムの実際の波速度を測定するには、いくつかの方法を用いることができる:
デュアル圧力センサー方式
- 既知の距離に圧力センサーを設置する
- 圧力パルスを発生させる(バルブを素早く開く)
- 各センサーの圧力上昇の遅延時間を測定
- 距離÷時間遅れで速度を計算する
共振周波数法
- 密閉チューブ内に圧力振動を発生させる
- 基本共振周波数(f)を測定する
- 閉端管について、c = 2Lfを用いて速度を計算する。
- 高調波(基本波の奇数倍)で検証する
反射タイミング法
- バルブの近くに圧力センサーを設置する
- バルブを素早く開いて圧力パルスを作る
- 最初のパルスと反射パルスの間の時間を測定
- 速度を2L÷反射時間として計算する。
ケーススタディシステム応答への波速の影響
空気圧式グリッパーを備えたロボット・エンドエフェクターの場合:
| パラメータ | オリジナルデザイン(5mライン) | 最適化設計(1mライン) | 改善 |
|---|---|---|---|
| ラインの長さ | 5メートル | 1メートル | 80%リダクション |
| 波の伝播時間 | 15.3 ms | 3.1 ms | 12.2ミリ秒速い |
| 圧力上昇時間 | 28ミリ秒 | 9ミリ秒 | 19ミリ秒速い |
| 握力の安定性 | ±12%のばらつき | ±3%のばらつき | 75%改善 |
| サイクルタイム | 1.2秒 | 0.95秒 | 21%高速化 |
| 生産率 | 3000部品/時間 | 3780部品/時間 | 26%増加 |
このケーススタディは、波の伝搬を理解し最適化することで、システムのパフォーマンスに大きな影響を与えることを実証している。
定在波の検証:共振周波数はどのように性能問題を引き起こすのか?
定在波は、圧力波が反射してそれ自身と干渉し、圧力の節点と反節点の固定パターンを作り出すときに発生します。これらの共振現象は、適切に理解・管理されなければ、空気圧システムに深刻な性能問題を引き起こす可能性があります。
空気圧システムにおける定在波は、圧力波が境界で反射して建設的に干渉し、圧力変動が増幅される共振周波数を作り出すときに発生します。これらの共振は、閉管の場合、f = nc/2Lの式に従います。ここで、nは調和数、cは波速度、Lは管長です。圧力センサー、加速度計、音響測定による実験的検証は、これらの理論的予測を確認し、効果的な緩和戦略を導く。
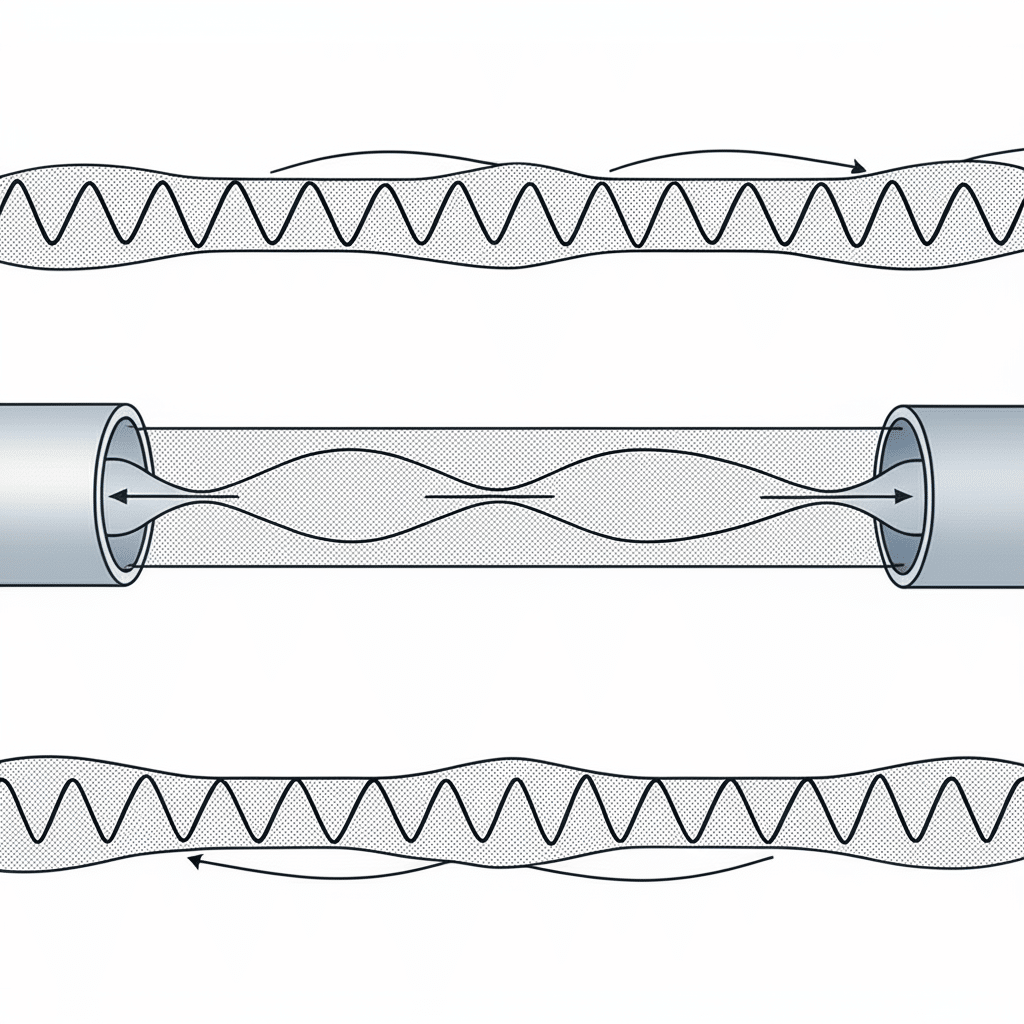
マサチューセッツ州の医療機器メーカーとの最近のプロジェクトでは、同社の精密空気圧位置決めシステムが特定の動作周波数で不思議な力の変動を示していました。定在波検証テストを実施したところ、2.1mの供給ラインに81Hzの基本共振があることが判明しました。この共振が320%の圧力変動を増幅していたのです。ラインの長さを1.8メートルに調整することで、共振周波数を同社の動作範囲からずらし、この問題を完全に解消し、位置決め精度を±0.8ミリメートルから±0.15ミリメートルに改善しました。
定在波の基礎
定在波は、入射波と反射波が干渉し、圧力ノード(最小変動)と反ノード(最大変動)の固定パターンが形成されるときに形成される。
空気圧ラインの共振周波数は境界条件に依存する:
両端が閉じたラインの場合(空気圧システムで最も一般的):
f = nc/2L
どこでだ:
- f = 共振周波数(Hz)
- n = 倍音数(1、2、3など)
- c = 波の速度(m/s)
- L = ラインの長さ(m)
一方の端が開いている線:
f = (2n-1)c/4L
両端が開いているラインの場合(空気圧では稀):
f = nc/2L
実験的検証方法
空気圧システムの定在波パターンを検証する技術はいくつかある:
マルチ圧力センサー・アレイ
- 空気圧ラインに沿って一定の間隔で圧力変換器を設置する。
- 周波数掃引またはインパルスでシステムを励起する。
- 各地点の圧力変動を記録する
- 圧力振幅と位置を対応させ、ノードとアンチノードを特定する。
- 測定された周波数を理論予測と比較する
音響相関
- 音響センサー(マイクロフォン)を使って、圧力変動から音を検出する
- 音響インテンシティと動作周波数の相関
- 共振周波数に対応する音の強さのピークを特定する
- ピークが予測された周波数で発生することを確認する。
加速度計による測定
- 空気圧ラインとコンポーネントに加速度ピックアップを取り付ける
- 周波数範囲の振動振幅を測定
- 振動スペクトルの共振ピークの特定
- 予測される定在波周波数との相関性
実用的な定在波周波数計算
典型的な空気圧システムの場合:
- ラインの長さ(L):3メートル
- 波速(c):343 m/s
- クローズドエンド構成
基本共振周波数はこうなる:
f₁ = c/2L = 343/(2×3) = 57.2 Hz
そして、ハーモニックスはこうなる:
f₂ = 2f₁ = 114.4 Hz
f₃ = 3f₁ = 171.6 Hz
f₄ = 4f₁ = 228.8 Hz
これらの周波数は、圧力変動が増幅される可能性のある潜在的な問題点を示している。
定在波パターンとその効果
| ハーモニック | ノード/アンチノード・パターン | システム効果 | 影響を受ける重要部品 |
|---|---|---|---|
| ファンダメンタル(n=1) | センターに1つの圧力反節 | 中間の圧力変動が大きい | インラインコンポーネント、継手 |
| 2番目(n=2) | 2つのアンチノード、中央のノード | 両端付近の圧力変動 | バルブ、アクチュエータ、レギュレータ |
| 3位(n=3) | 3つのアンチノード、2つのノード | 複雑な圧力パターン | 複数のシステム・コンポーネント |
| 第4位(n=4) | 4つのアンチノード、3つのノード | 高周波振動 | シール、小型部品 |
実験的検証ケーススタディ
性能が安定しない精密空気圧位置決めシステム用:
| パラメータ | 理論的予測 | 実験測定 | 相関性 |
|---|---|---|---|
| 基本周波数 | 81.2 Hz | 79.8 Hz | 98.3% |
| 第2高調波 | 162.4 Hz | 160.5 Hz | 98.8% |
| 第3高調波 | 243.6 Hz | 240.1 Hz | 98.6% |
| 圧力増幅 | レゾナンスで3:1(推定) | 共振時3.2:1(実測値) | 93.8% |
| ノードの位置 | 0、1.05、2.1メートル | 0、1.08、2.1メートル | 97.2% |
このケーススタディは、定在波現象の理論的予測と実験的測定との間の優れた一致を示している。
定在波の実用的意味合い
定在波は、空気圧システムにおいていくつかの重大な問題を引き起こす:
圧力増幅
- ゆらぎは共振で3~5倍に増幅される
- 部品の定格圧力を超えることがある
- アクチュエータに力の変動を生じさせるコンポーネントの疲労
- シールの摩耗を促進する高周波圧力サイクル
- 振動によるフィッティングの緩みと漏れ
- 深刻な場合、システムの寿命が30-70%短くなる不安定なコントロール
- フィードバック・システムは共振周波数で振動することがある。
- 位置と力の制御が予測不可能になる
- 自己強化振動を引き起こす可能性があるエネルギー損失
- 定在波は閉じ込められたエネルギーを表す
- エネルギー消費量を10-30%増加させることができる
- システム全体の効率を低下させる
パルス減衰法:破壊的な圧力振動を効果的に減衰させる技術とは?
圧力変動を制御することは、信頼性の高い空気圧システムの運転に不可欠です。問題となる圧力変動を低減または除去するために、さまざまな減衰方法を採用することができます。
空気圧システムにおける圧力パルスの減衰は、気体の圧縮によりエネルギーを吸収する容積チャンバー、粘性効果により減衰を発生させる制限エレメント、特定の周波数をキャンセルする同調共振器、カウンターパルスを発生させるアクティブキャンセルシステムなど、いくつかの方法によって達成することができます。効果的な減衰を実現するには、圧力変動の特定の周波数と振幅に合った方法を選択する必要があります。
私は最近、イリノイ州のある包装機器メーカーと仕事をしたのだが、その高速空気圧システムは圧力変動が激しく、シール力が一定しないことがあった。同社のエンジニアは基本的なレシーバータンクを試しましたが、成功しませんでした。詳細な圧力パルス解析により、そのシステムには異なる減衰アプローチを必要とする複数の周波数成分があることを突き止めました。を組み合わせたハイブリッドソリューションを導入することで、この問題を解決することができました。 ヘルムホルツ共振器5 その支配的な112Hzの振動と一連の制限オリフィスに調整することで、圧力変動を94%減少させ、シーリングの不一致を完全になくした。
基本的な減衰メカニズム
圧力パルスを減衰させるには、いくつかの物理的メカニズムを利用することができる:
体積ベースの減衰
気体の圧縮性によって機能する:
- 圧力エネルギーを吸収するコンプライアンス要素を提供する。
- 低周波変動に最も効果的
- 圧力損失を最小限に抑えたシンプルな実装
制限に基づく減衰
粘性散逸によって機能する:
- 摩擦によって圧力エネルギーを熱に変える
- 広い周波数範囲で有効
- 恒久的な圧力低下をもたらす
共振器ベースの減衰
同調破壊干渉によって機能する:
- 特定の周波数成分をキャンセルする
- 狙った周波数に高い効果
- 定常流への影響は最小限
素材ベースの減衰
壁の柔軟性とダンピングによって機能する:
- 壁の変形でエネルギーを吸収
- 広帯域減衰を提供
- 既存のコンポーネントに統合可能
ボリューム・チャンバー設計の原則
容積室(レシーバータンク)は最も一般的な減衰装置である:
ボリューム・チャンバーの有効性は、チャンバー容積とライン容積の比率に依存する:
減衰比 = 1 + (Vc/Vl)
どこでだ:
- Vc = チャンバー容積
- Vl = ラインの体積
周波数依存解析の場合、透過率は次のようになる:
TR = 1/√(1 + (ωVc/Zc)²)
どこでだ:
- ω=角周波数(2πf)
- Zc = 線路の特性インピーダンス
制限要素の減衰
オリフィス、多孔質材料、細長い通路は、粘性効果によって減衰を起こす:
制限を横切る圧力損失は次のようになる:
ΔP = k(ρv²/2)
どこでだ:
- k = 損失係数
- ρ = 気体密度
- v = 速度
減衰量は時間とともに増加する:
- より高い流速
- より大きな制限長
- 通路径が小さい
- より曲がりくねった流路
共振器減衰システム
同調レゾネーターは、狙った周波数を減衰させる:
ヘルムホルツ共振器
特定の周波数にチューニングされた、首の細い容積室:
f = (c/2π)√(A/VL)
どこでだ:
- f = 共振周波数
- c = 音速
- A = ネックの断面積
- V = チャンバー容積
- L = ネックの有効長
1/4波共振器
一端が開いている特定の長さの管:
f = c/4L
どこでだ:
- L = チューブの長さ
サイド・ブランチ共振器
複雑な周波数コンテンツに対応する複数の同調ブランチ:
- 各ブランチは特定の周波数をターゲットとする
- 複数の高調波に同時に対応可能
- メイン流路への影響は最小限
アクティブ・キャンセリング・システム
カウンターパルスを発生させる高度なシステム:
センシング・ステージ
- 入射圧力波を検出する
- 周波数コンテンツと振幅の分析加工段階
- 必要なキャンセル信号を計算する
- システムのダイナミクスと遅延を考慮する作動ステージ
- 逆圧波を発生させる
- 破壊的干渉の正確な時間
減衰性能の比較
| 方法 | 低周波(<50 Hz) | 中周波 (50-200 Hz) | 高周波(>200 Hz) | 圧力降下 | 複雑さ |
|---|---|---|---|---|---|
| ボリューム・チェンバー | エクセレント (>90%) | モデレート(40-70%) | 悪い (<30%) | 非常に低い | 低い |
| 制限オリフィス | 悪い (<30%) | 良好 (60-80%) | エクセレント (>80%) | 高い | 低い |
| ヘルムホルツ共振器 | 外の共鳴が悪い | レゾナンスに優れる | 外の共鳴が悪い | 低い | ミディアム |
| 1/4波管 | 外の共鳴が悪い | レゾナンスに優れる | 外の共鳴が悪い | 低い | ミディアム |
| マルチ共振器 | 中程度(40-60%) | エクセレント (>80%) | 良好 (60-80%) | 低い | 高い |
| アクティブ・キャンセル | エクセレント (>90%) | エクセレント (>90%) | 良い (70-85%) | なし | 非常に高い |
| ハイブリッド・システム | エクセレント (>90%) | エクセレント (>90%) | エクセレント (>90%) | 中程度 | 高い |
実用的な減衰の実装
効果的な圧脈減衰のために:
ゆらぎの特徴
- 振幅と周波数を測定する
- 支配的な周波数を特定する
- 広帯域の減衰が必要か、特定の周波数の減衰が必要かを判断する適切な方法を選択する
- 低周波用:ボリュームチャンバー
- 特定の周波数に同調共振器
- 広帯域減衰制限またはハイブリッドアプローチ
- クリティカルな用途にアクティブキャンセル配置の最適化
- 伝搬を防ぐために発生源の近くに置く
- デリケートな部品を保護するため、部品の近くに置く
- 定在波パターンを破壊するための戦略的な場所パフォーマンスの検証
- 減衰前後の測定
- 動作条件を確認する
- 意図しない結果を招かないようにする
ケーススタディ高速パッケージングにおける多方式減衰
圧力変動が発生する高速空気圧シールシステム用:
| パラメータ | 減衰前 | アフター・ボリューム・チェンバー | アフター・ハイブリッド・ソリューション | 改善 |
|---|---|---|---|---|
| 低周波(<50 Hz) | ±0.8 bar | ±0.12 bar | ±0.05バール | 94%リダクション |
| 中周波(112 Hz) | ±1.2 bar | ±0.85 bar | ±0.07 bar | 94%リダクション |
| 高周波(>200 Hz) | ±0.4 bar | ±0.36 bar | ±0.04 bar | 90%リダクション |
| シール力変動 | ±28% | ±22% | ±2.5% | 91%改善 |
| 製品不良率 | 4.2% | 3.1% | 0.3% | 93%リダクション |
| システム効率 | ベースライン | +4% | +12% | 12%改善 |
このケーススタディは、減衰に対する的を絞った複数の方法によるアプローチが、いかにシステムのパフォーマンスを劇的に向上させるかを実証している。
高度な減衰技術
特に困難な用途向け:
分散減衰
1つの大きな装置ではなく、複数の小さな装置を使う:
- ソースと高感度コンポーネントの両方に減衰を近づける
- 定在波パターンをより効果的に砕く
- 冗長性と安定したパフォーマンスを提供
周波数選択ダンピング
特定の問題周波数をターゲットにする:
- 異なる周波数に調整された複数のレゾネーターを使用
- 問題を排除しながら、望ましいシステム応答を維持する
- システム全体のパフォーマンスへの影響を最小限に抑える
適応システム
使用状況に応じて減衰量を調整:
- 圧力変動をモニターするセンサーを使用
- 減衰パラメーターを自動調整
- 様々な条件下でパフォーマンスを最適化
結論
圧力変動理論-波動伝播速度、定在波検証、パルス減衰法-を理解することは、信頼性が高く効率的な空気圧システム設計の基礎を提供します。これらの原理を適用することで、あらゆる運転条件下で安定した動作を保証しながら、不可解な性能問題を排除し、コンポーネントの寿命を延ばし、システム効率を向上させることができます。
空気圧システムの圧力変動に関するFAQ
圧力の変動は空気圧機器の寿命にどのような影響を与えますか?
圧力変動は、いくつかのメカニズムを通じてコンポーネントの寿命を著しく低下させます。圧力変動は、シーリング表面に微小運動を発生させることによってシールの摩耗を加速させ、応力サイクルの繰り返しによってダイアフラムやフレキシブルエレメントの材料疲労を誘発し、振動によってねじ接続部のゆるみを促進し、幾何学的な遷移部に局所的な応力集中を生じさせます。圧力変動が厳しく制御されていないシステムでは、適切に減衰されたシステムと比較して、一般的に40-70%の部品寿命が短くなり、シールとダイアフラムは特に脆弱です。
空気圧システムのライン長と圧力応答時間の関係は?
線路の長さは、単純な関係に従って圧力応答時間に直接影響します:応答時間は、波の伝播速度によって決まる割合で、線路の長さとともに直線的に増加します。標準的な条件(波速度≈343 m/s)の空気では、1メートルのラインごとに約2.9ミリ秒の伝送遅延が加わります。しかし、実際の圧力上昇時間は、圧力を均一化するために何度も反射する必要があるため、通常、最初の波動伝達時間の2~5倍長くなります。つまり、5メートルラインの送波時間は14.5ミリ秒だが、圧力上昇時間は30~70ミリ秒ということになる。
空気圧システムに共振による圧力変動が発生しているかどうかを確認するにはどうすればよいですか?
共振による圧力変動は、一般的にいくつかの観察可能な症状で現れます:コンポーネントが特定の動作周波数で振動するが、他の周波数では振動しない、動作条件のわずかな変化でシステム性能が一貫せずに変化する、空気圧ラインから「シンギング」または「ホイッスル音」が聞こえる、圧力計の測定値が振動する、アクチュエータの性能(速度、力)が周期的に変化する、などです。共振を確認するには、応答速度の速いトランスデューサー(応答時間<1ms)を使用してシステム内の異なるポイントで圧力を測定し、圧力振幅がラインに沿った位置によって変化する定在波パターンを探します。
圧力変動は空気圧システムのエネルギー効率に影響するか?
圧力変動はエネルギー効率に大きな影響を及ぼし、通常、いくつかのメカニズムによってエネルギー効率を10-25%低下させます。高いピーク圧力を発生させることによって漏れ率を増加させ、周期的な圧縮と膨張によってエネルギーを浪費し、振動によって部品の摩擦を増加させ、性能の問題を補うために供給圧力を増加させることがよくあります。さらに、圧力変動によって生じる乱流と流れの分離は、有用な圧力エネルギーを廃熱に変えます。圧力変動を適切に減衰させることで、他の変更を加えることなく、システム効率を5-15%向上させることができます。
温度変化は空気圧システムの圧力波の挙動にどのような影響を与えるか?
温度は、いくつかのメカニズムを通じて圧力波の挙動に大きな影響を与えます。波の伝搬速度に直接影響を与え(1℃上昇につき約+0.6m/s)、ガスの密度と粘度を変化させて減衰特性を変え、空気圧ラインの弾性特性を変化させて波の反射と透過に影響を与え、共振周波数をシフトさせます(1℃につき約+0.17%)。この温度感度は、20℃で完璧に作動するシステムが、40℃で作動すると問題のある共振が発生する可能性があることや、冬の条件に合わせて調整された減衰装置が夏には効果がない可能性があることを意味します。


