Koks yra plokščios sferos tūris pneumatinio cilindro reikmėms?

OSP-P serija Originalus modulinis cilindras be strypo — OSP mechaninis cilindras be strypo

Inžinieriai susiduria su painiava skaičiuodami suplokštėjusių sferinių komponentų tūrius pneumatinių cilindrų be strypų sistemose. Neteisingi tūrio skaičiavimai lemia neteisingus slėgio apskaičiavimus ir sistemos gedimus.

Plokščios sferos (oblate sferoid) tūris V = (4/3)πa²b, kur "a" yra ekvatorinis spindulys, o "b" - poliarinis spindulys. pneumatinis akumuliatorius¹ ir amortizacijos reikmėms.

Praėjusį mėnesį padėjau Andreasui, dizaino inžinieriui iš Vokietijos, kurio pneumatinės amortizacijos sistema sugedo, nes jis naudojo standartinį rutulio tūrį, o ne oblatinio sferoido skaičiavimus savo suplokštintoms akumuliatoriaus kameroms.

Turinys

Kas yra plokščia sfera pneumatinėse programose?
Kaip apskaičiuoti plokščiosios sferos tūrį?
Kur naudojamos plokščiosios sferos cilindruose be strypų?
Kokią įtaką tūriui ir našumui daro plokščioji plokštuma?

Kas yra plokščia sfera pneumatinėse programose?

Plokščia sfera, techniškai vadinama obliejinis sferoidas²tai trimatė forma, sukuriama suspaudus rutulį išilgai vienos ašies, dažniausiai naudojama pneumatinių akumuliatorių ir amortizatorių konstrukcijose.

Plokščioji sfera gaunama suploninus tobuląją sferą išilgai jos vertikalios ašies, taip sukuriant elipsės formos skerspjūvį su skirtingais horizontalaus ir vertikalaus spindulių matavimais.

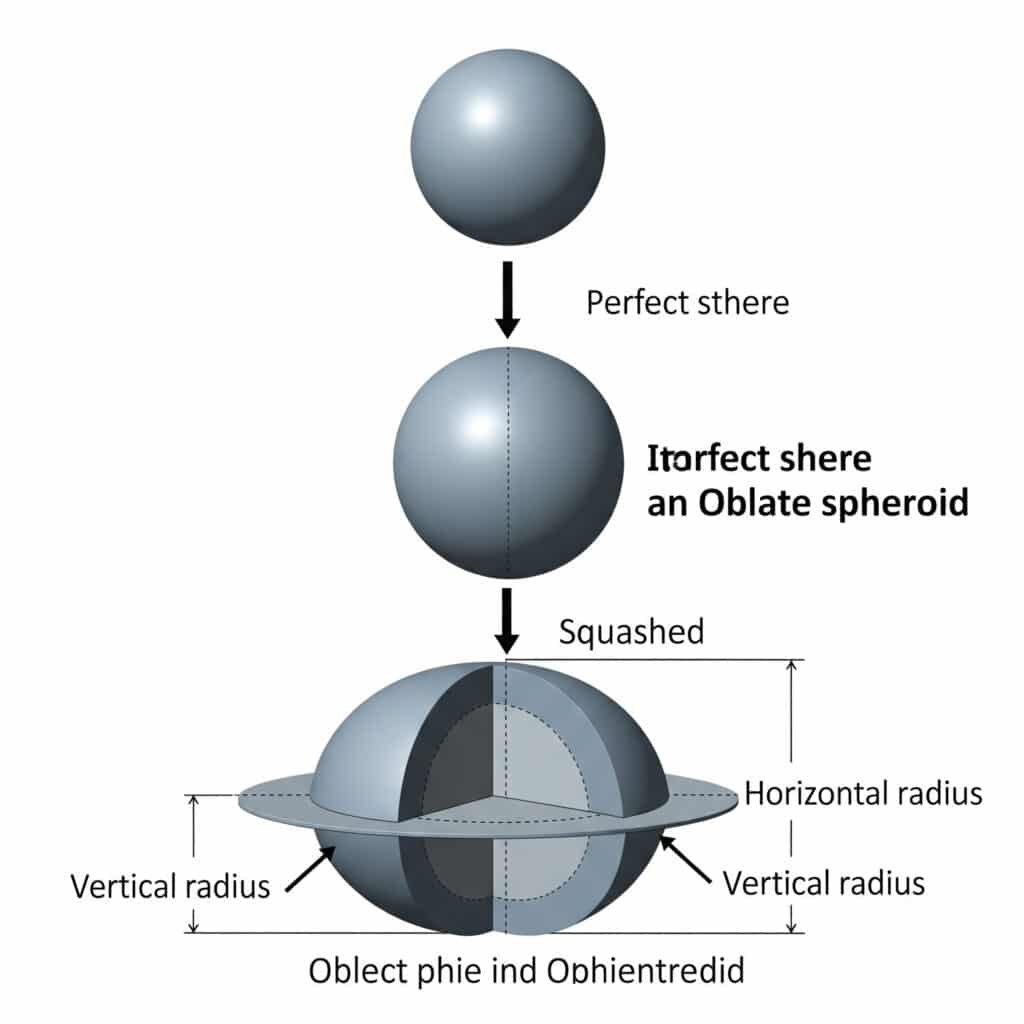
Trijų žingsnių schema, iliustruojanti tobulosios sferos virsmą plokščiąja sfera (plokščiuoju sferoidu). Procesas rodo, kad sfera suspaudžiama, todėl gaunama figūra su paryškintu skerspjūviu ir aiškiai pažymėtais skirtingo ilgio vertikaliaisiais ir horizontaliaisiais spinduliais. — Plokščiosios sferos diagrama, rodanti plokščiojo sferoido formą

Geometrinė apibrėžtis

Formos charakteristikos

Plokščiasis sferoidas: Techninis geometrinis terminas
Suplotas rutulys: Bendras pramoninis aprašymas
Elipsės formos profilis: Skerspjūvio vaizdas
Sukimosi simetrija: Aplink vertikaliąją ašį

Pagrindiniai matmenys

Pusiaujo spindulys (a): Horizontalusis spindulys (didesnis)
Poliarinis spindulys (b): Vertikalusis spindulys (mažesnis)
Išlyginimo koeficientas: b/a < 1,0
Aspect ratio (kraštinių santykis): Aukščio ir pločio santykis

Plokščia sfera ir tobula sfera

Charakteristika	Tobula sfera	Plokščia sfera
Forma	Vienodas spindulys	Suspaustas vertikaliai
Tūrio formulė	(4/3)πr³	(4/3)πa²b
Skerspjūvis	Apskritimas	Elipsė
Simetrija	Visos kryptys	Tik horizontaliai

Bendrieji sulygiavimo koeficientai

Šviesos išlyginimas

Santykis: b/a = 0,8-0,9
Paraiškos: Nedideli erdvės apribojimai
Poveikis apimčiai: 10-20% sumažinimas
Veikimas: Minimalus poveikis

Vidutinio laipsnio suplokštėjimas

Santykis: b/a = 0,6-0,8
Paraiškos: Standartinės akumuliatorių konstrukcijos
Poveikis apimčiai: 20-40% sumažinimas
Veikimas: Pastebimi slėgio pokyčiai

Stiprus išlyginimas

Santykis: b/a = 0,3-0,6
Paraiškos: Didelis erdvės apribojimas
Poveikis apimčiai: 40-70% sumažinimas
Veikimas: Svarbūs projektavimo aspektai

Pneumatinės programos

Akumuliatorių kameros

Susiduriu su plokščiomis sferomis:

Įrenginiai, kuriems trūksta vietos: Aukščio apribojimai
Integruoti dizainai: Įmontuoti į mašinų rėmus
Pasirinktinės programos: Specifiniai tūrio reikalavimai
Modernizavimo projektai: Esamų erdvių pritaikymas

Minkštinimo sistemos

Takto pabaigos slopinimas: Cilindrų be strypų naudojimas
Smūgio absorbcija: Poveikio apkrovos valdymas
Slėgio reguliavimas: Sklandus veikimo valdymas
Triukšmo mažinimas: Tylesnis sistemos veikimas

Gamybos aspektai

Gamybos metodai

Gilus piešimas: Lakštinio metalo formavimas
Hidroformavimas: Tikslus formavimo procesas
Apdirbimas: Individualūs vienetiniai komponentai
Liejimas: Didelės apimties gamyba

Medžiagų parinkimas

Plieno: Aukšto slėgio taikymas
Aliuminis: Svoriui jautrios konstrukcijos
Nerūdijantis plienas: Korozinė aplinka
Kompozitinės medžiagos: Specialieji reikalavimai

Kaip apskaičiuoti plokščiosios sferos tūrį?

Norint tiksliai suprojektuoti pneumatinę sistemą, plokščiosios sferos tūriui apskaičiuoti reikia taikyti oblate sferoido formulę, naudojant lygiašonio ir poliarinio spindulių matavimus.

Plokščiosios sferos tūriui tiksliai apskaičiuoti naudokite formulę V = (4/3)πa²b, kur "a" yra ekvatorinis spindulys (horizontalus), o "b" - poliarinis spindulys (vertikalus).

Tūrio formulės suskirstymas

Standartinė formulė

V = (4/3)πa²b

V: Tūris kubiniais vienetais
π: 3,14159 (matematinė konstanta)
a: Ekvatorinis spindulys (horizontalus)
b: Poliarinis spindulys (vertikalus)
4/3: Sferoido tūrio koeficientas

Formulės sudedamosios dalys

Pusiaujo sritis: πa² (horizontalus skerspjūvis)
Poliarinis mastelio keitimas: b koeficientas (vertikalus suspaudimas)
Tūrio koeficientas: 4/3 (geometrinė konstanta)
Rezultato vienetai: Atitinka įvesties spindulio vienetus kubu

Skaičiavimas žingsnis po žingsnio

Matavimo procesas

Išmatuokite ekvatorinį skersmenį: Plačiausias horizontalusis matmuo
Apskaičiuokite ekvatoriaus spindulį: a = skersmuo ÷ 2
Išmatuokite poliarinį skersmenį: Vertikalus aukščio matmuo
Apskaičiuokite poliarinį spindulį: b = aukštis ÷ 2
Taikyti formulę: V = (4/3)πa²b

Skaičiavimo pavyzdys

Pneumatiniam akumuliatoriui:

Ekvatorinis skersmuo: 100 mm → a = 50 mm
Poliarinis skersmuo: 60 mm → b = 30 mm
tomas: V = (4/3)π(50)²(30)
Rezultatas: V = (4/3)π(2500)(30) = 314,159 mm³

Tūrio apskaičiavimo pavyzdžiai

Ekvatorinis spindulys	Poliarinis spindulys	Išlyginimo santykis	tomas	Palyginimas su "Sphere
50 mm	50 mm	1.0	523,599 mm³	100% (tobula sfera)
50 mm	40 mm	0.8	418,879 mm³	80%
50 mm	30 mm	0.6	314 159 mm³	60%
50 mm	20 mm	0.4	209 440 mm³	40%

Skaičiavimo įrankiai

Rankinis skaičiavimas

Mokslinis skaičiuotuvas: Su π funkcija
Formulės tikrinimas: Dvigubai patikrinkite įvestis
Vieneto nuoseklumas: Visur išlaikyti tuos pačius vienetus
Tikslumas: Apskaičiuokite iki reikiamų skaičių po kablelio

Skaitmeniniai įrankiai

Inžinerinė programinė įranga: CAD tūrio skaičiavimai
Internetinės skaičiuoklės: Oblokštieji sferoidiniai įrankiai
Skaičiuoklės formulės: Automatiniai skaičiavimai
Mobiliosios programėlės: Lauko skaičiavimo įrankiai

Dažniausiai pasitaikančios skaičiavimo klaidos

Matavimo klaidos

Spindulys ir skersmuo: Neteisingo matmens naudojimas
Ašių painiava: Horizontalių ir vertikalių matavimų derinimas
Vieneto nenuoseklumas: mm vs coliai maišymas
Tikslumo praradimas: Per ankstyvas apvalinimas

Formulės klaidos

Klaidinga formulė: Naudojant sferą vietoj sferoido
Parametrų keitimas: a ir b verčių sukeitimas vietomis
Koeficientų klaidos: Trūksta 4/3 veiksnio
π aproksimacija: Naudojant 3.14 vietoj 3.14159

Patikrinimo metodai

Kryžminės patikros metodai

CAD programinė įranga: 3D modelio tūrio skaičiavimas
Vandens išstūmimas: Fizikinis tūrio matavimas
Keli skaičiavimai: Įvairių metodų palyginimas
Gamintojo specifikacijos: Paskelbti apimties duomenys

Pagrįstumo patikros

Tūrio mažinimas: Turėtų būti mažiau nei tobula sfera
Niveliuojanti koreliacija: Didesnė plokštuma = mažesnis tūris
Vieneto patikrinimas: Rezultatai atitinka tikėtiną dydį
Taikymo tinkamumas: Tomas atitinka sistemos reikalavimus

Kai padėjau Marijai, pneumatinių sistemų projektuotojai iš Ispanijos, apskaičiuoti akumuliatorių tūrius jos bepakopio cilindro įrengimui, nustatėme, kad jos pirminiuose skaičiavimuose buvo naudojamos sferos, o ne oblate sferoido formulės, todėl 35% tūris buvo pervertintas ir sistema veikė netinkamai.

Kur naudojamos plokščiosios sferos cilindruose be strypų?

Plokščiosios sferos naudojamos įvairiuose pneumatinių cilindrų be strypų komponentuose, kai dėl vietos apribojimų reikia optimizuoti tūrį, išlaikant slėginio indo funkcionalumą.

Plokščios sferos paprastai naudojamos akumuliatorių kamerose, amortizacijos sistemose ir integruotuose slėginiuose induose, esančiuose cilindrų be strypų mazguose, kai aukščio apribojimai riboja standartines sferines konstrukcijas.

Akumuliatorių programos

Integruoti akumuliatoriai

Erdvės optimizavimas: Tinka mašinų rėmuose
Tūrio efektyvumas: Didžiausias sandėliavimo plotas ribotame aukštyje
Slėgio stabilumas: Sklandus veikimas paklausos piko metu
Sistemos integracija: Įmontuota į cilindrų montavimo pagrindus

Modernizavimo įrengimai

Esamos mašinos: Aukščio aukščio apribojimai
Atnaujinimo projektai: Kaupimo įtraukimas į senesnes sistemas
Erdvės apribojimai: Darbas pagal pirminį projektą
Veiklos tobulinimas: Geresnis sistemos atsakas

Minkštinimo sistemos

Takto pabaigos slopinimas

Įrengiu plokščią rutulinę pagalvėlę:

Magnetiniai cilindrai be lazdelių: Sklandus lėtėjimas
Valdomi cilindrai be lazdelių: Poveikio mažinimas
Dvigubo veikimo cilindrai be lazdelių: Dviejų krypčių amortizacija
Didelės spartos taikomosios programos: Smūgių slopinimas

Slėgio reguliavimas

Srauto išlyginimas: Pašalinti slėgio šuolius
Triukšmo mažinimas: Tylesnis veikimas
Komponentų apsauga: Mažesnis nusidėvėjimas ir įtampa
Sistemos stabilumas: Nuoseklus veikimas

Specializuoti komponentai

Slėginiai indai

Pasirinktinės programos: Unikalūs erdvės reikalavimai
Daugiafunkciniai dizainai: Kombinuotas laikymas ir montavimas
Modulinės sistemos: Sukabinamos konfigūracijos
Prieiga prie techninės priežiūros: Tinkami naudoti dizainai

Jutiklių kameros

Slėgio stebėjimas: Integruotos matavimo sistemos
Srauto aptikimas: Greičio jutiklio taikymas
Sistemos diagnostika: Veiklos stebėjimas
Saugos sistemos: Slėgio mažinimo integravimas

Dizaino aspektai

Erdvės apribojimai

Paraiška	Aukščio riba	Tipiškas išlyginimas	Poveikis apimčiai
Montavimas po grindimis	50 mm	b/a = 0,3	70% sumažinimas
Mašinų integracija	100 mm	b/a = 0,6	40% sumažinimas
Modernizavimo programos	150 mm	b/a = 0,8	20% sumažinimas
Standartinis montavimas	200 mm ir daugiau	b/a = 0,9	10% sumažinimas

Veiklos reikalavimai

Slėgio įvertinimas: Išlaikyti struktūrinį vientisumą
Tūrio talpa: Patenkinkite sistemos poreikį
Srauto charakteristikos: Tinkamas įleidimo ir išleidimo angos dydis
Prieiga prie techninės priežiūros: Eksploatavimo aspektai

Įrengimo pavyzdžiai

Pakavimo mašinos

Paraiška: Greitaeigė pildymo įranga
Apribojimas: 40 mm aukščio tarpas
Sprendimas: Stipriai suplokštėjęs akumuliatorius (b/a = 0,25)
Rezultatas: 75% tūrio sumažinimas, tinkamas veikimas

Automobilių surinkimas

Paraiška: Robotų padėties nustatymo sistema
Apribojimas: Integravimas į robotų bazę
Sprendimas: Vidutinio laipsnio suplokštėjimas (b/a = 0,7)
Rezultatas: 30% taupoma vieta, išlaikomas našumas

Maisto perdirbimas

Paraiška: Sanitarinių cilindrų be lazdelių sistema
Apribojimas: Plovimo aplinkos leidimas
Sprendimas: Pasirinktinis plokščios sferos dizainas
Rezultatas: IP69K reitingas³ su optimizuotu tūriu

Gamybos specifikacijos

Standartiniai dydžiai

Mažas: 50 mm ekvatorinis, įvairūs poliariniai matmenys
Vidutinis: 100 mm ekvatorinis, aukščio svyravimai
Didelis: 200 mm ekvatorinis, pagal užsakymą parenkamas poliarinis dydis
Pasirinktinis: Konkretiems taikymams būdingi matmenys

Medžiagų parinktys

Anglinis plienas: Standartinis slėgis
Nerūdijantis plienas: Korozinė aplinka
Aliuminis: Svoriui jautrūs įrenginiai
Sudėtinis: Specialieji reikalavimai

Praėjusiais metais dirbau su mašinų gamintoju Thomu iš Šveicarijos, kuriam reikėjo akumuliatorių saugyklos jo kompaktiškos pakavimo linijai. Standartiniai sferiniai akumuliatoriai nebūtų tilpę į 60 mm aukščio apribojimą, todėl sukūrėme plokščius sferinius akumuliatorius, kurių santykis b/a = 0,4. Taip pasiekėme 60% pradinio tūrio, o kartu laikėmės visų erdvės apribojimų.

Kokią įtaką tūriui ir našumui daro plokščioji plokštuma?

Plokštumas gerokai sumažina tūrio talpą, kartu darydamas įtaką slėgio dinamikai, srauto charakteristikoms ir bendram sistemos veikimui belazdėse pneumatinėse sistemose.

Kiekvienas 10% padidėjęs išlyginimas (b/a santykio sumažėjimas) sumažina tūrį apytiksliai 10% ir turi įtakos reakcijai į slėgį, srauto modeliams ir sistemos efektyvumui pneumatiniuose akumuliatoriuose.

Tūrio poveikio analizė

Tūrio mažinimo santykiai

Tūrio santykis = (b/a), kai sferoidai yra plokšti

Linijinis ryšys: Tūris mažėja proporcingai plokštėjant
Numatomas poveikis: Lengva apskaičiuoti tūrio pokyčius
Dizaino lankstumas: Pasirinkite optimalų išlyginimo santykį
Kompromisai dėl našumo: Erdvės ir pajėgumų balansas

Kiekybiniai tūrio pokyčiai

Išlyginimo santykis (b/a)	Tūrio išlaikymas	Tūrio praradimas	Taikymo tinkamumas
0.9	90%	10%	Puikus
0.8	80%	20%	Labai gerai
0.7	70%	30%	Geras
0.6	60%	40%	Sąžiningai
0.5	50%	50%	Prastas
0.4	40%	60%	Labai prastas

Slėgio poveikis našumui

Reakcijos į slėgį charakteristikos

Sumažintas tūris: Greitesni slėgio pokyčiai
Didesnis jautrumas: Geriau reaguoja į srauto pokyčius
Dažnesnis važiavimas dviračiu: Dažnesni įkrovimo / iškrovimo ciklai
Sistemos nestabilumas: Potencialūs slėgio svyravimai

Slėgio skaičiavimo koregavimai

P₁V₁ = P₂V₂ (Boilio dėsnis⁴ taikoma)

Mažesnis tūris: Didesnis slėgis tai pačiai oro masei
Slėgio svyravimai: Didesni svyravimai darbo metu
Sistemos dydžio nustatymas: Kompensuoti didesniu kompresoriaus pajėgumu
Saugumo ribos: Didesni slėgio vardiniai reikalavimai

Srauto charakteristikos

Srauto modelio pokyčiai

Turbulencijos padidėjimas: Dėl suplotos formos atsiranda srauto sutrikimų
Slėgio kritimas: Didesnis pasipriešinimas dėl deformuotų kamerų
Įleidimo ir išleidimo poveikis: Uosto padėties nustatymas tampa labai svarbus
Srauto greitis: Didesnis greitis ribotuose ruožuose

Srauto greičio poveikis

Sumažėjęs efektyvusis plotas: Atsiranda srauto apribojimų
Slėgio nuostoliai: Mažėja energijos vartojimo efektyvumas
Reakcijos laikas: Lėtesnis užpildymo ir išleidimo greitis
Sistemos veikimas: Bendras efektyvumo sumažėjimas

Struktūriniai aspektai

Įtampos pasiskirstymas

Koncentruotas stresas: Didesnės apkrovos išlygintuose plotuose
Medžiagos storis: Gali prireikti sutvirtinimo
Atsparumas nuovargiui⁵: Sumažėjęs ciklo trukmės potencialas
Saugos veiksniai: Reikalingos didesnės projektavimo maržos

Slėgio įvertinimo poveikis

Išlyginimo santykis	Streso padidėjimas	Rekomenduojamas saugos koeficientas	Medžiagos storis
0.9	10%	1.5	Standartinis
0.8	25%	1.8	+10%
0.7	45%	2.0	+20%
0.6	70%	2.5	+35%

Sistemos našumo optimizavimas

Kompensavimo strategijos

Didesnis akumuliatoriaus kiekis: Keli mažesni vienetai
Didesnio slėgio veikimas: Kompensuoti tūrio praradimą
Patobulinta srauto konstrukcija: Optimizuoti įleidimo ir išleidimo įtaisų konfigūracijas
Sistemos derinimas: Sureguliuokite valdymo parametrus

Veiklos stebėjimas

Slėgio ciklų dažnis: Stebėti sistemos stabilumą
Srauto greičio matavimai: Patikrinkite, ar pakankamas pajėgumas
Temperatūros poveikis: Patikrinkite, ar nėra per didelio įkaitimo
Techninės priežiūros intervalai: Koreguoti pagal veiklos rezultatus

Projektavimo gairės

Optimalus išlyginimo pasirinkimas

b/a > 0,8: Minimalus poveikis našumui
b/a = 0,6-0,8: Priimtinas daugumai programų
b/a = 0,4-0,6: Reikia kruopštaus sistemos projektavimo
b/a < 0,4: Paprastai nerekomenduojama

Rekomendacijos dėl konkrečių programų

Didelio dažnio važiavimas dviračiu: Minimizuoti suplokštėjimą (b/a > 0,7)
Erdvei svarbūs įrenginiai: Priimkite kompromisus dėl našumo
Saugai svarbios sistemos: Konservatyvūs išlyginimo koeficientai
Sąnaudoms jautrūs projektai: Balansas tarp našumo ir vietos taupymo

Realaus veikimo duomenys

Atvejo analizės rezultatai

Išanalizavęs 50 įrenginių su įvairiais išlyginimo koeficientais našumo duomenis:

10% išlyginimas: Nereikšmingas poveikis našumui
30% išlyginimas: 15% dviračių važiavimo dažnio padidėjimas
50% išlyginimas: 40% sumažintas efektyvusis pajėgumas
70% išlyginimas: Sistemos nestabilumas 60% atvejų

Optimizavimo sėkmė

Elenai, sistemos integratorei iš Italijos, optimizavome jos cilindrų be strypų akumuliatoriaus konstrukciją, apribodami išlyginimą iki b/a = 0,75, taip sutaupydami 25% vietos ir išlaikydami 95% pradinį sistemos našumą bei pašalindami slėgio nestabilumo problemas.

Išvada

Plokščios sferos tūriui naudojama formulė V = (4/3)πa²b, kurios ekvatorinis spindulys "a" ir poliarinis spindulys "b". Suplokštinimas proporcingai sumažina tūrį, tačiau turi įtakos slėgio reakcijai ir srauto charakteristikoms pneumatiniuose įrenginiuose.

DUK apie plokščią sferos tūrį

Kokia yra plokščiosios sferos tūrio formulė?

Plokščiosios sferos (plokščiojo sferoido) tūrio formulė V = (4/3)πa²b, kur "a" yra ekvatorinis spindulys (horizontalus), o "b" - poliarinis spindulys (vertikalus). Tai skiriasi nuo tobulosios sferos formulės V = (4/3)πr³.

Kiek tūrio prarandama suplokštinant rutulį?

Tūrio sumažėjimas lygus suplonėjimo santykiui. Jei poliarinis spindulys yra 70% ekvatorinio spindulio (b/a = 0,7), tūris tampa 70% pradinio rutulio tūrio, t. y. tūris sumažėja 30%.

Kur pneumatinėse sistemose naudojamos plokščios sferos?

Plokščios sferos naudojamos akumuliatorių kamerose, amortizacijos sistemose ir slėginiuose induose, kai aukščio apribojimai riboja standartines sferines konstrukcijas. Dažniausiai jos naudojamos integruojant į ribotos erdvės mašinas ir modernizuojant įrenginius.

Kaip išlyginimas veikia pneumatinį veikimą?

Išlyginimas sumažina tūrio talpą, padidina jautrumą slėgiui ir sukelia srauto turbulenciją. Sistemose, kuriose akumuliatoriai labai suplokštėję (b/a < 0,6), gali atsirasti slėgio nestabilumas ir sumažėti efektyvumas, dėl kurio reikia projektinio kompensavimo.

Koks didžiausias rekomenduojamas išlyginimo santykis?

Pneumatiniams įrenginiams, kad būtų pasiektas priimtinas našumas, išlyginimo santykis turi būti didesnis nei b/a = 0,6. Mažesni nei 0,4 santykiai paprastai sukelia sistemos nestabilumą, o norint užtikrinti tinkamą veikimą, reikia gerokai pakeisti konstrukciją.

Suprasti pneumatinių akumuliatorių funkciją ir paskirtį skysčių galios sistemose. ↩
Sužinokite matematinį apibrėžimą ir geometrines netaisyklingo sferoido savybes. ↩
Žr. oficialų IP69K apsaugos nuo įsiskverbimo laipsnio apibrėžimą ir bandymų reikalavimus. ↩
Apžvelkite Boilio dėsnio, apibūdinančio dujų slėgio ir tūrio priklausomybę, principus. ↩
Išnagrinėkite atsparumo nuovargiui sąvoką ir medžiagų elgseną veikiant ciklinei apkrovai. ↩

Sveiki, esu Chuckas, vyresnysis ekspertas, turintis 15 metų patirtį pneumatikos pramonėje. Bendrovėje "Bepto Pneumatic" daugiausia dėmesio skiriu aukštos kokybės, mūsų klientams pritaikytų pneumatinių sprendimų teikimui. Mano kompetencija apima pramonės automatizavimą, pneumatinių sistemų projektavimą ir integravimą, taip pat pagrindinių komponentų taikymą ir optimizavimą. Jei turite klausimų arba norėtumėte aptarti savo projekto poreikius, nedvejodami kreipkitės į mane el. paštu chuck@bepto.com.