
Vai esat kādreiz pamanījis noslēpumainas vibrācijas savās pneimatiskajās līnijās? Vai neizskaidrojamas spēka svārstības cilindros, neraugoties uz stabilu padeves spiedienu? Šīs parādības nav nejaušas - tās ir spiediena viļņu rezultāts, kas izplatās jūsu sistēmā, radot sekas, kas var būt dažādas - no nelielas neefektivitātes līdz katastrofālām kļūmēm.
Spiediena svārstības pneimatiskajās sistēmās ir viļņu parādības, kas izplatās ar ātrumu, kas tuvojas ātrumam. skaņas ātrums1, radot dinamiskus efektus, tostarp rezonansi, stāvviļņi2un spiediena pastiprināšana. Izpratne par šīm svārstībām ir ļoti svarīga, jo tās var izraisīt komponentu nogurumu, vadības nestabilitāti un nestabilitāti. enerģijas zudumi 10-25% tipiskās rūpnieciskās sistēmās.3.
Pagājušajā mēnesī konsultēju kādu automobiļu montāžas rūpnīcu Tenesī, kur kritiski svarīga pneimatiskā saspiešanas sistēma piedzīvoja nepārtrauktas spēka svārstības, neraugoties uz stabilu piegādes spiedienu. Tehniskās apkopes komanda bija nomainījusi vārstus, regulatorus un pat visu sistēmu. gaisa sagatavošanas iekārta4 bez panākumiem. Analizējot spiediena viļņu dinamiku, jo īpaši stāvviļņu modeļus padeves līnijās, mēs konstatējām, ka tie darbojas ar frekvenci, kas cilindrā rada destruktīvu interferenci. Vienkārša līnijas garuma korekcija novērsa šo problēmu un ietaupīja vairākas nedēļas ražošanas aizkavēšanās. Ļaujiet man parādīt, kā spiediena svārstību teorijas izpratne var mainīt jūsu pneimatisko sistēmu uzticamību.
Satura rādītājs
- Viļņu izplatīšanās ātrums: Cik ātri spiediena traucējumi pārvietojas jūsu sistēmā?
- Stāvviļņu verifikācija: Kā rezonanses frekvences rada veiktspējas problēmas?
- Impulsu vājināšanas metodes: Kādi paņēmieni efektīvi slāpē postošās spiediena svārstības?
- Secinājums
- Bieži uzdotie jautājumi par spiediena svārstībām pneimatiskajās sistēmās
Viļņu izplatīšanās ātrums: Cik ātri spiediena traucējumi pārvietojas jūsu sistēmā?
Lai prognozētu un kontrolētu spiediena traucējumu ietekmi, ir svarīgi saprast, cik ātri tie izplatās pneimatiskajās sistēmās. No izplatīšanās ātruma ir atkarīgs sistēmas reakcijas laiks, rezonanses frekvences un iespējamie destruktīvie traucējumi.
Spiediena viļņi pneimatiskajās sistēmās pārvietojas ar skaņas ātrumu gāzes vidē, ko var aprēķināt pēc formulas c = √(γRT), kur γ ir īpatnējais siltuma koeficients, R ir īpatnējā gāzes konstante un T ir absolūtā temperatūra. Gaisam 20 °C temperatūrā tas ir aptuveni 343 m/s, lai gan šo ātrumu maina tādi faktori kā caurules elastība, gāzes saspiežamība un plūsmas apstākļi.
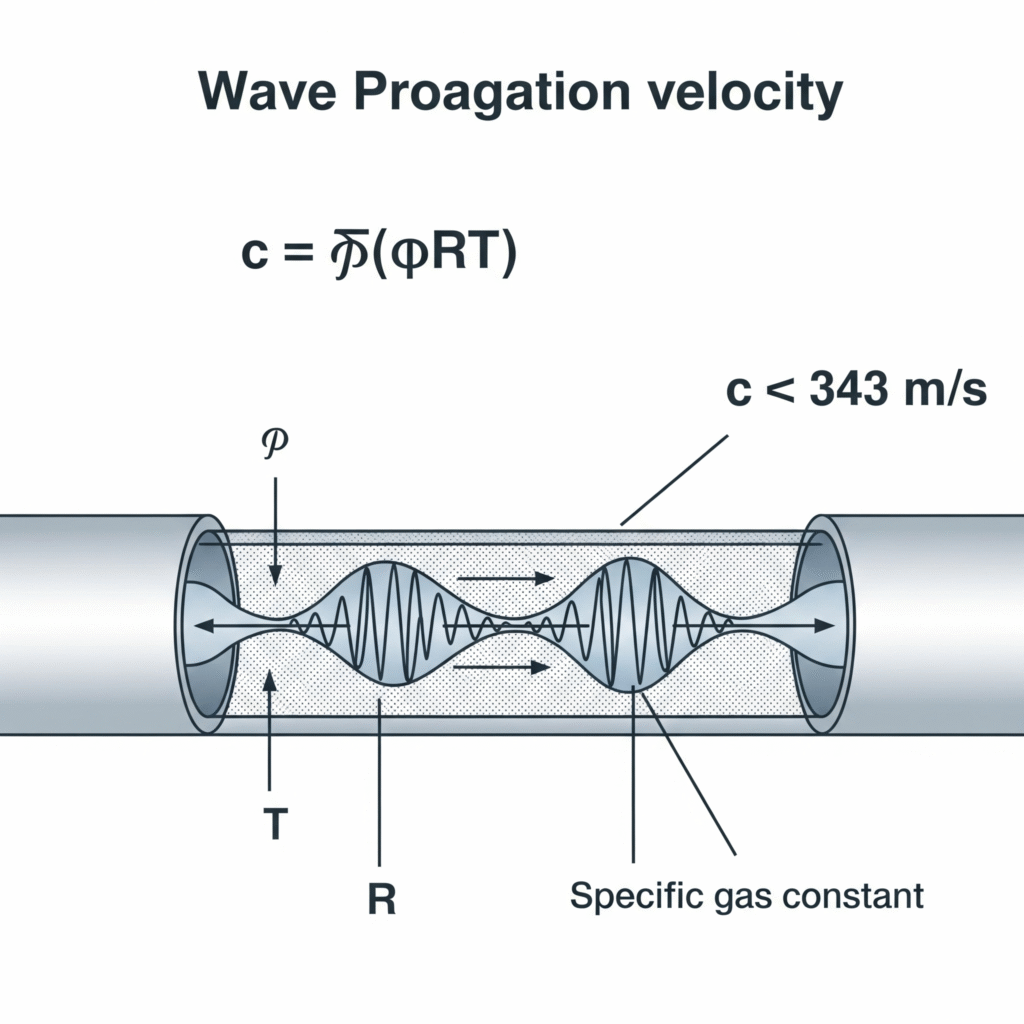
Nesen palīdzēju novērst traucējumus precīzas montāžas iekārtā Šveicē, kur pneimatiskajiem satvērējiem bija 12 ms aizkave starp aktivizēšanu un spēka pielietošanu - mūžīga parādība ātrdarbīgā ražošanas vidē. Inženieri bija pieņēmuši, ka spiediens tiek pārnests uzreiz. Mērot faktisko viļņu izplatīšanās ātrumu viņu sistēmā (328 m/s) un ņemot vērā 4 metru līnijas garumu, mēs aprēķinājām, ka teorētiskais pārraides laiks ir 12,2 ms - gandrīz precīzi atbilst novērotajai aizturei. Ventiļu pārvietošana tuvāk pie izpildmehānismiem samazināja šo aizkavi līdz 3 ms un palielināja ražošanas ātrumu par 14%.
Viļņu ātruma pamatvienādojumi
Spiediena viļņu izplatīšanās ātruma gāzes vidē pamatvienādojums ir šāds:
c = √(γRT)
Kur:
- c = viļņu izplatīšanās ātrums (m/s)
- γ = īpatnējā siltuma koeficients (1,4 gaisam)
- R = īpatnējā gāzes konstante (287 J/kg-K gaisam)
- T = absolūtā temperatūra (K)
Gaisam 20°C (293K) temperatūrā iegūst:
c = √(1,4 × 287 × 293) = 343 m/s
Modificētais viļņu ātrums pneimatiskajās līnijās
Reālās pneimatiskajās sistēmās efektīvo viļņu ātrumu maina caurules elastība un citi faktori saskaņā ar formulu:
c_eff = c / √(1 + (Dψ/Eh))
Kur:
- c_eff = efektīvais viļņu ātrums (m/s)
- D = caurules diametrs (m)
- ψ = gāzes saspiežamības koeficients
- E = caurules materiāla elastības modulis (Pa)
- h = Caurules sieniņu biezums (m)
Temperatūras un spiediena ietekme uz viļņu ātrumu
Viļņu ātrums mainās atkarībā no ekspluatācijas apstākļiem:
| Temperatūra | Spiediens | Viļņu ātrums gaisā | Praktiskā nozīme |
|---|---|---|---|
| 0°C (273K) | 1 bārs | 331 m/s | Lēnāka reakcija aukstā vidē |
| 20°C (293K) | 1 bārs | 343 m/s | Standarta atsauces stāvoklis |
| 40°C (313K) | 1 bārs | 355 m/s | Ātrāka reakcija siltā vidē |
| 20°C (293K) | 6 bāri | 343 m/s* | Spiedienam ir minimāla tieša ietekme uz ātrumu. |
* Piezīme: Lai gan pamatviļņu ātrums nav atkarīgs no spiediena, faktisko ātrumu reālās sistēmās var ietekmēt spiediena izraisītas izmaiņas cauruļu elastībā un gāzes uzvedībā.
Praktiskais viļņu izplatīšanās laika aprēķins
Pneimatiskajai sistēmai ar:
- Līnijas garums (L): 5 metri
- Darba temperatūra: 20°C (c = 343 m/s)
- Cauruļu materiāls: Poliuretāna caurule (maina ātrumu par aptuveni 5%)
Efektīvais viļņu ātrums būtu:
c_eff = 343 × 0,95 = 326 m/s
Un viļņu izplatīšanās laiks būtu:
t = L/c_eff = 5/326 = 0,0153 sekundes (15,3 milisekundes)
Tas ir minimālais laiks, kas nepieciešams, lai spiediena maiņa no viena līnijas gala nokļūtu līdz otram - kritisks faktors ātrgaitas lietojumos.
Viļņu ātruma mērīšanas metodes
Pneimatisko sistēmu faktiskā viļņu ātruma mērīšanai var izmantot vairākas metodes:
Divu spiediena sensoru metode
- Spiediena sensoru uzstādīšana zināmos attālumos cits no cita
- Radiet spiediena impulsu (ātra vārsta atvēršana).
- Laika aizkaves mērīšana starp spiediena paaugstināšanos katrā sensorā
- Aprēķināt ātrumu kā attālumu, kas dalīts ar laika aizturi.
Rezonanses frekvences metode
- Spiediena svārstību radīšana slēgtā caurulē
- Izmēriet pamatrezonanses frekvenci (f)
- Aprēķiniet ātrumu, izmantojot c = 2Lf caurulei ar slēgtu galu.
- Pārbaudiet ar harmoniskajām (nepāra reizinātājiem ar fundamentālo)
Atspoguļošanas laika metode
- Spiediena sensora uzstādīšana vārsta tuvumā
- Radiet spiediena impulsu, ātri atverot vārstu.
- Laika mērīšana starp sākotnējo impulsu un atstaroto impulsu
- Aprēķina ātrumu kā 2L dalītu ar atstarošanas laiku.
Gadījuma izpēte: Viļņu ātruma ietekme uz sistēmas reakciju
Robotam ar pneimatiskiem satvērējiem:
| Parametrs | Sākotnējais dizains (5m līnijas) | Optimizēts dizains (1 m līnijas) | Uzlabojumi |
|---|---|---|---|
| Līnijas garums | 5 metri | 1 metrs | 80% samazinājums |
| Viļņu izplatīšanās laiks | 15,3 ms | 3,1 ms | 12,2 ms ātrāk |
| Spiediena veidošanās laiks | 28 ms | 9 ms | 19 ms ātrāk |
| Satvēriena spēka stabilitāte | ±12% izmaiņas | ±3% izmaiņas | 75% uzlabojums |
| Cikla laiks | 1,2 sekundes | 0,95 sekundes | 21% ātrāk |
| Ražošanas ātrums | 3000 gabalu stundā | 3780 daļas stundā | 26% palielinājums |
Šis gadījuma pētījums parāda, kā viļņu izplatīšanās izpratne un optimizācija var būtiski ietekmēt sistēmas veiktspēju.
Stāvviļņu verifikācija: Kā rezonanses frekvences rada veiktspējas problēmas?
Stāvviļņi rodas, kad spiediena viļņi atstaro un interferē paši ar sevi, veidojot nemainīgus spiediena mezglu un antinodu modeļus. Šīs rezonanses parādības var radīt nopietnas darbības problēmas pneimatiskajās sistēmās, ja tās netiek pareizi izprastas un pārvaldītas.
Pneimatiskajās sistēmās pastāvīgie viļņi rodas, kad spiediena viļņi atstarojas pie robežām un konstruktīvi interferē, radot rezonanses frekvences, kurās spiediena svārstības pastiprinās. Šīs rezonanses slēgtām caurulēm atbilst formulai f = nc/2L, kur n ir harmoniskais skaitlis, c ir viļņu ātrums, bet L ir caurules garums. Eksperimentālā verifikācija, izmantojot spiediena sensorus, akselerometrus un akustiskos mērījumus, apstiprina šīs teorētiskās prognozes un nosaka efektīvas ietekmes mazināšanas stratēģijas.
Nesen Masačūsetsas štatā, Masačūsetsas štatā, tika īstenots projekts ar medicīnas ierīču ražotāju, kura precīzās pneimatiskās pozicionēšanas sistēmai pie noteiktām darbības frekvencēm bija vērojamas noslēpumainas spēka svārstības. Veicot stāvviļņu verifikācijas testus, mēs konstatējām, ka 2,1 metru garajā barošanas līnijā pamatrezonanse ir 81 Hz - precīzi sakrīt ar izpildmehānisma cikliskuma frekvenci. Šī rezonanse pastiprināja spiediena svārstības par 320%. Pielāgojot līnijas garumu līdz 1,8 metriem, mēs novirzījām rezonanses frekvenci no to darbības diapazona un pilnībā novērsām šo problēmu, uzlabojot pozicionēšanas precizitāti no ±0,8 mm līdz ±0,15 mm.
Pastāvīgā viļņa pamati
Stāvviļņi veidojas, kad krītošie un atstarotie viļņi interferē, radot nemainīgus spiediena mezglu (minimālas svārstības) un antinodu (maksimālas svārstības) modeļus.
Pneimatiskās līnijas rezonanses frekvences ir atkarīgas no robežstāvokļiem:
līnijai ar slēgtiem galiem (visbiežāk sastopama pneimatiskajās sistēmās):
f = nc/2L
Kur:
- f = rezonanses frekvence (Hz)
- n = Harmoniskais skaitlis (1, 2, 3 utt.)
- c = viļņa ātrums (m/s)
- L = līnijas garums (m)
Attiecībā uz līniju ar vienu atvērtu galu:
f = (2n-1)c/4L
līnijai ar abiem atvērtiem galiem (reti sastopams pneimatikā):
f = nc/2L
Eksperimentālās verifikācijas metodes
Ar vairākiem paņēmieniem var pārbaudīt stāvviļņu modeļus pneimatiskajās sistēmās:
Vairāku spiediena sensoru masīvs
- Regulārās vietās gar pneimatisko līniju uzstādiet spiediena devējus.
- Sistēmas uzbudināšana ar frekvences svārstību vai impulsu.
- Reģistrēt spiediena svārstības katrā vietā
- Spiediena amplitūdas un stāvokļa attiecību kartēšana, lai noteiktu mezglus un antinodus.
- Salīdziniet izmērītās frekvences ar teorētiskajām prognozēm.
Akustiskā korelācija
- Akustisko sensoru (mikrofonu) izmantošana, lai noteiktu skaņu no spiediena svārstībām.
- Atbilstība starp skaņas intensitāti un darba frekvenci
- Noteikt skaņas intensitātes maksimumus, kas atbilst rezonanses frekvencēm.
- Pārbaudiet, vai pīķi parādās prognozētajās frekvencēs.
Akselerometra mērījumi
- Akcelerometru uzstādīšana uz pneimatiskajām līnijām un sastāvdaļām
- Vibrācijas amplitūdas mērīšana visā frekvenču diapazonā
- Identificēt rezonanses maksimumus vibrāciju spektrā
- Korelē ar prognozētajām stāvviļņu frekvencēm
Praktiska pastāvīgā viļņa frekvences aprēķināšana
Tipiskai pneimatiskai sistēmai ar:
- Līnijas garums (L): 3 metri
- Viļņu ātrums (c): 343 m/s
- Slēgto galu konfigurācija
Pamatrezonanses frekvence būtu:
f₁ = c/2L = 343/(2×3) = 57,2 Hz
Un harmonikas būtu šādas:
f₂ = 2f₁ = 114,4 Hz
f₃ = 3f₁ = 171,6 Hz
f₄ = 4f₁ = 228,8 Hz
Šīs frekvences ir potenciāli problemātiski punkti, kuros spiediena svārstības var pastiprināties.
Stāvviļņu modeļi un to ietekme
| Harmoniskā | Mezglu/apakšmezglu modelis | Sistēmas ietekme | Skartie kritiskie komponenti |
|---|---|---|---|
| Fundamentālie (n=1) | Viens spiediena antinods centrā | Lielas spiediena svārstības līnijas vidusdaļā | In-line komponenti, piederumi |
| Otrais (n=2) | Divi antinodi, mezgls centrā | Spiediena svārstības galu tuvumā | Vārsti, piedziņas, regulatori |
| Trešais (n=3) | Trīs antinodi, divi mezgli | Sarežģīts spiediena modelis | Vairāki sistēmas komponenti |
| Ceturtais (n=4) | Četri antinodi, trīs mezgli | Augstas frekvences svārstības | Blīvējumi, mazas detaļas |
Eksperimentālās verifikācijas gadījuma izpēte
Precīzai pneimatiskajai pozicionēšanas sistēmai, kas darbojas nekonsekventi:
| Parametrs | Teorētiskās prognozes | Eksperimentālie mērījumi | Korelācija |
|---|---|---|---|
| Pamatfrekvence | 81,2 Hz | 79,8 Hz | 98.3% |
| Otrā harmoniskā | 162,4 Hz | 160,5 Hz | 98.8% |
| Trešā harmoniskā | 243,6 Hz | 240,1 Hz | 98.6% |
| Spiediena pastiprināšana | 3:1 rezonansē (aprēķināts) | 3,2:1 rezonansē (izmērīts) | 93.8% |
| Mezglu atrašanās vietas | 0, 1,05, 2,1 metri | 0, 1,08, 2,1 metri | 97.2% |
Šis gadījuma pētījums demonstrē lielisku teorētisko prognožu un eksperimentālo mērījumu atbilstību stāvviļņu parādībām.
Stāvviļņu praktiskās sekas
Pneimatiskajās sistēmās stāvošie viļņi rada vairākas būtiskas problēmas:
Spiediena pastiprināšana
- Svārstības rezonansē var pastiprināt 3-5×.
- Var pārsniegt komponentu nominālo spiedienu
- Veido spēka svārstības izpildmehānismosSastāvdaļu nogurums
- Augstas frekvences spiediena cikliskums paātrina blīvējuma nodilumu
- Vibrācija izraisa montāžas atslābināšanos un noplūdi
- Smagos gadījumos sistēmas kalpošanas laiks samazinās par 30-70%.Vadības nestabilitāte
- atgriezeniskās saites sistēmas var svārstīties rezonanses frekvencēs.
- Pozīcijas un spēka kontrole kļūst neprognozējama
- Var radīt pašpastiprinošas svārstības.Enerģijas zudumi
- Stāvviļņi ir iesprostota enerģija
- Var palielināt enerģijas patēriņu par 10-30%
- Samazina kopējo sistēmas efektivitāti
Impulsu vājināšanas metodes: Kādi paņēmieni efektīvi slāpē postošās spiediena svārstības?
Spiediena svārstību kontrole ir būtiska drošai pneimatiskās sistēmas darbībai. Lai samazinātu vai novērstu problemātiskās spiediena svārstības, var izmantot dažādas vājināšanas metodes.
Spiediena impulsu slāpēšanu pneimatiskajās sistēmās var panākt ar vairākām metodēm: tilpuma kamerām, kas absorbē enerģiju, saspiežot gāzi, ierobežojošiem elementiem, kas rada slāpēšanu ar viskozes efektu, regulētiem rezonatoriem, kas slāpē noteiktas frekvences, un aktīvām slāpēšanas sistēmām, kas rada pretpulsu. Lai slāpēšana būtu efektīva, metode ir jāpielāgo spiediena svārstību īpašajam frekvenču saturam un amplitūdai.
Nesen strādāju ar kādu iepakojuma iekārtu ražotāju Ilinoisas štatā, kura ātrgaitas pneimatiskajā sistēmā bija vērojamas lielas spiediena svārstības, kas izraisīja nekonsekventu blīvēšanas spēku. Viņu inženieri bija izmēģinājuši pamata uztvērējtvertnes, bet bez panākumiem. Veicot detalizētu spiediena impulsu analīzi, mēs noskaidrojām, ka viņu sistēmai ir vairākas frekvenču komponentes, kurām nepieciešamas dažādas vājināšanas metodes. Īstenojot hibrīdrisinājumu, kas apvieno Helmholca rezonators5 noskaņoti uz to dominējošajām 112 Hz svārstībām un virkni ierobežojošo atveru, mēs samazinājām spiediena svārstības par 94% un pilnībā novērsām blīvēšanas neatbilstības.
Fundamentālie vājināšanas mehānismi
Spiediena impulsu vājināšanai var izmantot vairākus fizikālus mehānismus:
Uz tilpumu balstīta vājināšanās
Darbojas, izmantojot gāzes saspiežamību:
- Nodrošina atbilstības elementu, kas absorbē spiediena enerģiju.
- Visefektīvākais zemas frekvences svārstību gadījumā
- Vienkārša realizācija ar minimālu spiediena kritumu
Uz ierobežojumiem balstīta vājināšana
Darbojas, izmantojot viskozu izkliedi:
- Berzes rezultātā spiediena enerģija tiek pārvērsta siltumā.
- Efektīvs plašā frekvenču diapazonā
- Veido pastāvīgu spiediena kritumu
Uz rezonatoru balstīta vājināšana
Darbojas, izmantojot noregulētu destruktīvu interferenci:
- Anulē konkrētas frekvences sastāvdaļas
- Ļoti efektīvs mērķtiecīgām frekvencēm
- Minimāla ietekme uz plūsmu vienmērīgā stāvoklī
Uz materiāliem balstīta vājināšanās
Darbojas, izmantojot sienu elastību un amortizāciju:
- Absorbē enerģiju, deformējot sienu
- Nodrošina platjoslas vājinājumu
- Var integrēt esošajos komponentos
Tilpuma kameras konstrukcijas principi
Visizplatītākās vājināšanas ierīces ir tilpuma kameras (uztvērējtvertnes):
Tilpuma kameras efektivitāte ir atkarīga no kameras tilpuma attiecības pret līnijas tilpumu:
Izkliedes koeficients = 1 + (Vc/Vl)
Kur:
- Vc = kameras tilpums
- Vl = līnijas tilpums
No frekvences atkarīgai analīzei pārraides koeficients ir:
TR = 1/√(1 + (ωVc/Zc)²)
Kur:
- ω = leņķa frekvence (2πf)
- Zc = līnijas raksturīgā pretestība
Ierobežojošā elementa slāpēšana
Caurumiem, porainiem materiāliem un garām šaurām ejām rodas vājināšanās viskozes ietekmē:
Spiediena kritums caur ierobežojumu ir šāds:
ΔP = k(ρv²/2)
Kur:
- k = zudumu koeficients
- ρ = Gāzes blīvums
- v = ātrums
Nodrošinātais vājinājums palielinās līdz ar:
- Lielāks plūsmas ātrums
- Lielāks ierobežojuma garums
- Mazāks eju diametrs
- Sarežģītāks plūsmas ceļš
Rezonatoru slāpēšanas sistēmas
Noregulēti rezonatori nodrošina mērķtiecīgu frekvenču slāpēšanu:
Helmholca rezonators
Skaļuma kamera ar šauru kakliņu, kas noregulēta uz noteiktu frekvenci:
f = (c/2π)√(A/VL)
Kur:
- f = rezonanses frekvence
- c = skaņas ātrums
- A = kakla šķērsgriezuma laukums
- V = kameras tilpums
- L = efektīvais kakla garums
Ceturtdaļviļņu rezonators
Noteikta garuma caurule ar atvērtu vienu galu:
f = c/4L
Kur:
- L = caurules garums
Sānu atzaru rezonatori
Vairāki noregulēti atzari sarežģītam frekvenču saturam:
- Katrs atzars ir vērsts uz konkrētu frekvenci.
- Vienlaikus var novērst vairākas harmonikas
- Minimāla ietekme uz galveno plūsmas ceļu
Aktīvās atcelšanas sistēmas
Uzlabotas sistēmas, kas ģenerē pretpulkus:
Uztveršanas posms
- Atpazīt ienākošos spiediena viļņus
- Analizēt frekvences saturu un amplitūduApstrādes posms
- Aprēķināt nepieciešamo atcelšanas signālu
- Sistēmas dinamikas un kavējumu ņemšana vērāPiedziņas posms
- Izveidot pretspiediena viļņus
- Precīzs laiks destruktīvai interferencei
Izkliedes veiktspējas salīdzinājums
| Metode | Zema frekvence (<50 Hz) | Vidējā frekvence (50-200 Hz) | Augsta frekvence (>200 Hz) | Spiediena kritums | Sarežģītība |
|---|---|---|---|---|---|
| Tilpuma kamera | Lieliska (>90%) | Mēreni (40-70%) | Slikts (<30%) | Ļoti zems | Zema |
| Ierobežojošā diafragma | Slikts (<30%) | Labi (60-80%) | Lielisks (>80%) | Augsts | Zema |
| Helmholca rezonators | Slikta ārējā rezonanse | Izcila rezonanse | Slikta ārējā rezonanse | Zema | Vidēja |
| Ceturtdaļviļņu caurule | Slikta ārējā rezonanse | Izcila rezonanse | Slikta ārējā rezonanse | Zema | Vidēja |
| Vairāki rezonatori | Mēreni (40-60%) | Lielisks (>80%) | Labi (60-80%) | Zema | Augsts |
| Aktīva atcelšana | Lieliska (>90%) | Lieliska (>90%) | Labi (70-85%) | Nav | Ļoti augsts |
| Hibrīdās sistēmas | Lieliska (>90%) | Lieliska (>90%) | Lieliska (>90%) | Mērens | Augsts |
Praktiska vājināšanas īstenošana
Efektīvai spiediena impulsa slāpēšanai:
Raksturojiet svārstības
- Amplitūdas un frekvences satura mērīšana
- Identificēt dominējošās frekvences
- Noteikt, vai nepieciešams vājināt platjoslas vai konkrētas frekvences.Atbilstošu metožu izvēle
- Zemām frekvencēm: Skaļuma kameras
- Konkrētām frekvencēm: Noregulēti rezonatori
- Platjoslas vājināšanai: Ierobežojumi vai hibrīda pieeja
- Kritiskiem lietojumiem: Aktīvā atcelšanaOptimizēt izvietošanu
- avotu tuvumā, lai novērstu izplatīšanos
- jutīgu komponentu tuvumā, lai tos aizsargātu
- Stratēģiskās vietās, lai pārtrauktu stāvviļņu veidošanos.Pārbaudiet veiktspēju
- Mērījums pirms/pēc vājināšanas
- Apstipriniet visos darbības apstākļos
- Nodrošināt, lai nerastos neparedzētas sekas
Gadījuma izpēte: Vairāku metožu vājināšanās ātrgaitas iepakojumā
Ātrgaitas pneimatiskās blīvēšanas sistēmai, kurā vērojamas spiediena svārstības:
| Parametrs | Pirms vājināšanas | Pēc tilpuma kameras | Pēc hibrīda risinājuma | Uzlabojumi |
|---|---|---|---|---|
| Zema frekvence (<50 Hz) | ±0,8 bar | ±0,12 bar | ±0,05 bar | 94% samazinājums |
| Vidējā frekvence (112 Hz) | ±1,2 bāri | ±0,85 bar | ±0,07 bar | 94% samazinājums |
| Augsta frekvence (>200 Hz) | ±0,4 bar | ±0,36 bar | ±0,04 bar | 90% samazinājums |
| Blīvējuma spēka izmaiņas | ±28% | ±22% | ±2.5% | 91% uzlabošana |
| Produktu noraidījumu skaits | 4.2% | 3.1% | 0.3% | 93% samazinājums |
| Sistēmas efektivitāte | Pamatlīnija | +4% | +12% | 12% uzlabojumi |
Šis gadījuma pētījums parāda, kā mērķtiecīga, vairāku metožu pieeja vājināšanai var ievērojami uzlabot sistēmas veiktspēju.
Uzlabotas vājināšanas metodes
Īpaši sarežģītiem lietojumiem:
Izkliedētais vājinājums
Vairāku mazāku ierīču izmantošana, nevis vienas lielas ierīces izmantošana:
- Novieto vājināšanu tuvāk avotiem un jutīgajiem komponentiem.
- Efektīvāk izjauc stāvviļņu modeļus
- Nodrošina dublēšanu un stabilāku veiktspēju
Frekvences selektīvā slāpēšana
Konkrētu problemātisku frekvenču noteikšana:
- Izmanto vairākus rezonatorus, kas noregulēti dažādām frekvencēm.
- Saglabāt vēlamo sistēmas reakciju, vienlaikus novēršot problēmas
- Minimizē ietekmi uz kopējo sistēmas veiktspēju
Adaptīvās sistēmas
Vājinājuma pielāgošana atkarībā no darba apstākļiem:
- Izmanto sensorus, lai uzraudzītu spiediena svārstības.
- Automātiski pielāgo vājināšanas parametrus
- Optimizē veiktspēju dažādos apstākļos
Secinājums
Spiediena svārstību teorijas - viļņu izplatīšanās ātruma, stāvviļņu pārbaudes un impulsu vājināšanas metožu - izpratne ir pamats uzticamas un efektīvas pneimatiskās sistēmas projektēšanai. Piemērojot šos principus, jūs varat novērst noslēpumainas veiktspējas problēmas, pagarināt komponentu kalpošanas laiku un uzlabot sistēmas efektivitāti, vienlaikus nodrošinot vienmērīgu darbību visos darba apstākļos.
Bieži uzdotie jautājumi par spiediena svārstībām pneimatiskajās sistēmās
Kā spiediena svārstības ietekmē pneimatisko komponentu kalpošanas ilgumu?
Spiediena svārstības ievērojami samazina komponentu kalpošanas ilgumu, izmantojot vairākus mehānismus: tās paātrina blīvējuma nodilumu, radot mikrokustības uz blīvējuma virsmām; tās izraisa materiālu nogurumu diafragmās un elastīgajos elementos atkārtotu sprieguma ciklu dēļ; tās veicina vītņsavienojumu atslābšanu vibrācijas dēļ; un tās rada lokālu sprieguma koncentrāciju ģeometriskās pārejās. Sistēmās ar lielām nekontrolētām spiediena svārstībām parasti ir īsāks komponentu 40-70% kalpošanas laiks salīdzinājumā ar pareizi amortizētām sistēmām, un īpaši neaizsargātas ir blīves un diafragmas.
Kāda ir saistība starp līnijas garumu un spiediena reakcijas laiku pneimatiskajās sistēmās?
Līnijas garums tieši ietekmē spiediena reakcijas laiku, ievērojot vienkāršu sakarību: reakcijas laiks lineāri palielinās līdz ar līnijas garumu ar ātrumu, ko nosaka viļņu izplatīšanās ātrums. Gaisam standarta apstākļos (viļņu ātrums ≈ 343 m/s) katrs līnijas metrs palielina pārraides aizkavi par aptuveni 2,9 milisekundēm. Tomēr faktiskais spiediena veidošanās laiks parasti ir 2-5 reizes ilgāks par sākotnējo viļņu pārraides laiku, jo spiediena izlīdzināšanai nepieciešami vairāki atstarojumi. Tas nozīmē, ka 5 metru līnijā viļņu pārraides laiks var būt 14,5 ms, bet spiediena veidošanās laiks - 30-70 ms.
Kā noteikt, vai manā pneimatiskajā sistēmā ir rezonanses spiediena svārstības?
Rezonanses spiediena svārstības parasti izpaužas ar vairākiem novērojamiem simptomiem: komponenti vibrē noteiktās darba frekvencēs, bet ne citās; sistēmas veiktspēja mainās nekonsekventi ar nelielām darba apstākļu izmaiņām; pneimatiskās līnijas dzirdami "dzied" vai "svilpo"; spiediena mērītāji uzrāda svārstīgus rādījumus; un izpildmehānisma veiktspēja (ātrums, spēks) cikliski mainās. Lai apstiprinātu rezonansi, izmēriet spiedienu dažādos sistēmas punktos, izmantojot ātras reakcijas devējus (reakcijas laiks < 1 ms), un meklējiet stāvviļņu modeļus, kuros spiediena amplitūda mainās atkarībā no pozīcijas līnijā.
Vai spiediena svārstības ietekmē pneimatisko sistēmu energoefektivitāti?
Spiediena svārstības būtiski ietekmē energoefektivitāti, parasti samazinot to par 10-25%, izmantojot vairākus mehānismus: tās palielina noplūdes rādītājus, radot augstāku maksimālo spiedienu; tās izšķērdē enerģiju cikliskai saspiešanai un izplešanai; tās izraisa paaugstinātu berzi detaļās vibrācijas dēļ; un tās bieži liek operatoriem palielināt padeves spiedienu, lai kompensētu darbības problēmas. Turklāt spiediena svārstību radītā turbulence un plūsmas atdalīšana pārvērš lietderīgo spiediena enerģiju siltuma zudumos. Pareizi slāpējot spiediena svārstības, var uzlabot sistēmas efektivitāti par 5-15% bez citām izmaiņām.
Kā temperatūras izmaiņas ietekmē spiediena viļņu uzvedību pneimatiskajās sistēmās?
Temperatūra būtiski ietekmē spiediena viļņu uzvedību, izmantojot vairākus mehānismus: tā tieši ietekmē viļņu izplatīšanās ātrumu (aptuveni +0,6 m/s uz °C pieaugumu); tā maina gāzes blīvumu un viskozitāti, mainot slāpēšanas īpašības; tā maina pneimatisko līniju elastīgās īpašības, ietekmējot viļņu atstarošanu un pārraidi; un tā maina rezonanses frekvences (aptuveni +0,17% uz °C). Šī jutība pret temperatūru nozīmē, ka sistēma, kas perfekti darbojas 20 °C temperatūrā, var radīt problemātiskas rezonanses, ja tā darbojas 40 °C temperatūrā, vai ka slāpēšanas ierīces, kas pielāgotas ziemas apstākļiem, vasarā var būt neefektīvas.
-
Sniegts detalizēts skaidrojums par skaņas ātruma fizikas likumsakarībām, kā to aprēķina un kādi faktori to ietekmē. ↩
-
Sniedz pamatus izpratnei par stāvviļņu parādībām, tostarp par to, kā tie veidojas no interferences, un to galvenajām īpašībām, piemēram, mezgliem un antinodiem. ↩
-
Sniegti pierādījumi un nozares pētījumi, kas apliecina tipisko enerģijas zudumu diapazonu, ko izraisa neefektivitāte, piemēram, spiediena svārstības pneimatiskajās sistēmās. ↩
-
Paskaidro gaisa sagatavošanas iekārtas (FRL), kas ir būtiska gaisa kvalitātes uzturēšanai pneimatiskajās sistēmās, sastāvdaļas un funkcijas. ↩
-
Sniegts padziļināts skaidrojums par Helmholca rezonatora, kas ir būtiska ierīce mērķtiecīgai frekvenču vājināšanai akustiskās un šķidrumu sistēmās, darbības principiem. ↩


