
Har du noen gang lagt merke til mystiske vibrasjoner i trykkledningene dine? Eller uforklarlige kraftvariasjoner i sylindrene til tross for stabilt forsyningstrykk? Disse fenomenene er ikke tilfeldige - de er et resultat av trykkbølger som forplanter seg gjennom systemet og skaper effekter som kan variere fra mindre ineffektivitet til katastrofale feil.
Trykksvingninger i pneumatiske systemer er bølgefenomener som forplanter seg med hastigheter som nærmer seg lydens hastighet1og skaper dynamiske effekter, inkludert resonans, stående bølger2og trykkforsterkning. Det er avgjørende å forstå disse svingningene fordi de kan føre til utmatting av komponenter, ustabil styring og energitap på 10-25% i typiske industrisystemer3.
I forrige måned var jeg konsulent for en bilmonteringsfabrikk i Tennessee, der et kritisk pneumatisk klemmesystem opplevde intermitterende kraftvariasjoner til tross for stabilt forsyningstrykk. Vedlikeholdsteamet hadde byttet ut ventiler, regulatorer og til og med hele luftforberedelsesenhet4 uten å lykkes. Ved å analysere trykkbølgedynamikken - spesielt de stående bølgemønstrene i tilførselsledningene - fant vi ut at de opererte med en frekvens som skapte ødeleggende interferens ved sylinderen. En enkel justering av linjelengden eliminerte problemet og sparte dem for flere uker med produksjonsforsinkelser. La meg vise deg hvordan forståelse av teorien om trykksvingninger kan endre påliteligheten til pneumatiksystemet ditt.
Innholdsfortegnelse
- Bølgeforplantningshastighet: Hvor raskt beveger trykkforstyrrelser seg i systemet ditt?
- Verifisering av stående bølger: Hvordan skaper resonansfrekvenser ytelsesproblemer?
- Metoder for pulsdemping: Hvilke teknikker demper effektivt destruktive trykksvingninger?
- Konklusjon
- Vanlige spørsmål om trykksvingninger i pneumatiske systemer
Bølgeforplantningshastighet: Hvor raskt beveger trykkforstyrrelser seg i systemet ditt?
Å forstå hvor raskt trykkforstyrrelser forplanter seg gjennom pneumatiske systemer er avgjørende for å kunne forutsi og kontrollere effekten av dem. Forplantningshastigheten bestemmer systemets responstid, resonansfrekvenser og potensialet for destruktiv interferens.
Trykkbølger i pneumatiske systemer beveger seg med lydens hastighet i gassmediet, som kan beregnes ved hjelp av formelen c = √(γRT), der γ er det spesifikke varmeforholdet, R er den spesifikke gasskonstanten og T er den absolutte temperaturen. For luft ved 20 °C tilsvarer dette ca. 343 m/s, selv om denne hastigheten modifiseres av faktorer som rørets elastisitet, gassens kompressibilitet og strømningsforholdene.
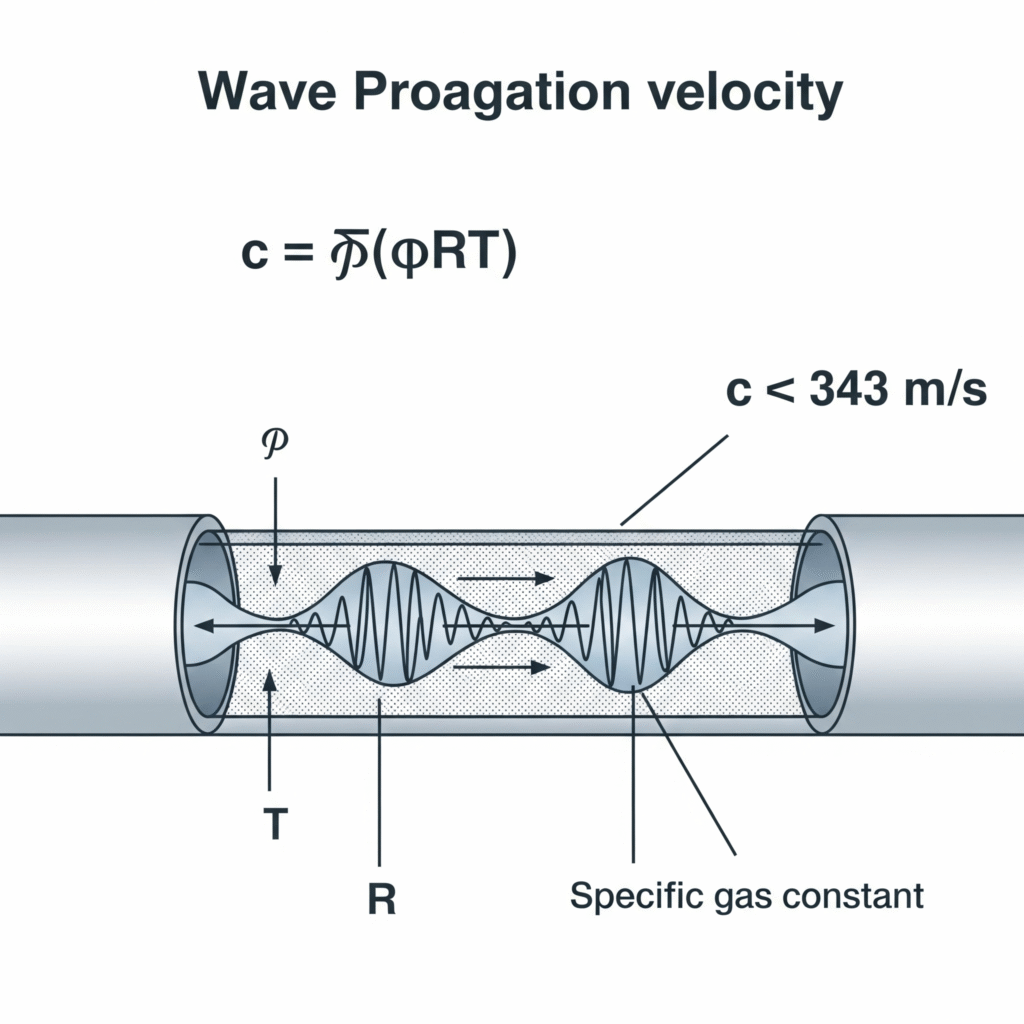
Jeg hjalp nylig til med feilsøking på en presisjonsmonteringsmaskin i Sveits, der pneumatiske gripere opplevde en forsinkelse på 12 ms mellom aktivering og kraftpåføring - en evighet i et produksjonsmiljø med høy hastighet. Ingeniørene hadde antatt at trykkoverføringen skjedde momentant. Ved å måle den faktiske bølgeforplantningshastigheten i systemet (328 m/s) og ta hensyn til linjelengden på 4 meter, beregnet vi en teoretisk overføringstid på 12,2 ms - noe som nesten nøyaktig samsvarte med den observerte forsinkelsen. Ved å flytte ventilene nærmere aktuatorene ble denne forsinkelsen redusert til 3 ms, og produksjonshastigheten økte med 14%.
Fundamentale ligninger for bølgehastighet
Den grunnleggende ligningen for trykkbølgens utbredelseshastighet i en gass er
c = √(γRT)
Hvor?
- c = Bølgeforplantningshastighet (m/s)
- γ = Spesifikt varmeforhold (1,4 for luft)
- R = Spesifikk gasskonstant (287 J/kg-K for luft)
- T = Absolutt temperatur (K)
For luft ved 20 °C (293 K) gir dette
c = √(1,4 × 287 × 293) = 343 m/s
Modifisert bølgehastighet i pneumatiske ledninger
I virkelige pneumatiske systemer modifiseres den effektive bølgehastigheten av rørets elastisitet og andre faktorer i henhold til formelen:
c_eff = c / √(1 + (Dψ/Eh))
Hvor?
- c_eff = Effektiv bølgehastighet (m/s)
- D = Rørdiameter (m)
- ψ = Kompressibilitetsfaktor for gass
- E = Rørmaterialets elastisitetsmodul (Pa)
- h = Rørveggens tykkelse (m)
Temperatur- og trykkeffekter på bølgehastighet
Bølgehastigheten varierer med driftsbetingelsene:
| Temperatur | Trykk | Bølgehastighet i luft | Praktiske implikasjoner |
|---|---|---|---|
| 0 °C (273 K) | 1 bar | 331 m/s | Langsommere respons i kalde omgivelser |
| 20 °C (293 K) | 1 bar | 343 m/s | Standard referansebetingelse |
| 40 °C (313 K) | 1 bar | 355 m/s | Raskere respons i varme omgivelser |
| 20 °C (293 K) | 6 bar | 343 m/s* | Trykket har minimal direkte effekt på hastigheten |
*Merk: Selv om den grunnleggende bølgehastigheten er uavhengig av trykk, kan den effektive hastigheten i virkelige systemer påvirkes av trykkinduserte endringer i rørets elastisitet og gassens oppførsel.
Praktisk beregning av bølgenes utbredelsestid
For et pneumatisk system med:
- Linjelengde (L): 5 meter
- Driftstemperatur: 20 °C (c = 343 m/s)
- Rørmateriale: Polyuretanrør (endrer hastigheten med ca. 5%)
Den effektive bølgehastigheten vil være:
c_eff = 343 × 0,95 = 326 m/s
Og bølgenes forplantningstid vil være
t = L/c_eff = 5/326 = 0,0153 sekunder (15,3 millisekunder)
Dette representerer den minste tiden det tar for en trykkendring å forflytte seg fra den ene enden av ledningen til den andre - en kritisk faktor i høyhastighetsapplikasjoner.
Teknikker for måling av bølgehastighet
Det finnes flere metoder for å måle den faktiske bølgehastigheten i pneumatiske systemer:
Metode med to trykksensorer
- Installer trykksensorer på kjente avstander fra hverandre
- Opprett en trykkpuls (rask ventilåpning)
- Mål tidsforsinkelsen mellom trykkstigning ved hver sensor
- Beregn hastighet som avstand dividert med tidsforsinkelse
Resonansfrekvensmetoden
- Skap trykksvingninger i et lukket rør
- Mål den grunnleggende resonansfrekvensen (f)
- Beregn hastigheten ved hjelp av c = 2Lf for et rør med lukket ende
- Verifiser med overtoner (oddetallsmultipler av grunntonen)
Metode for refleksjonstidspunkt
- Installer en trykksensor i nærheten av en ventil
- Opprett en trykkpuls ved å åpne ventilen raskt
- Mål tiden mellom startpuls og reflektert puls
- Beregn hastigheten som 2L dividert med refleksjonstiden
Casestudie: Bølgehastighetens innvirkning på systemresponsen
For en robot-endeeffektor med pneumatiske gripere:
| Parameter | Opprinnelig design (5 m linjer) | Optimalisert design (1 m linjer) | Forbedring |
|---|---|---|---|
| Linjelengde | 5 meter | 1 meter | 80% reduksjon |
| Bølgeutbredelsestid | 15,3 ms | 3,1 ms | 12,2 ms raskere |
| Tid for trykkoppbygging | 28 ms | 9 ms | 19 ms raskere |
| Stabilitet i grepskraften | ±12%-variasjon | ±3%-variasjon | 75% forbedring |
| Syklustid | 1,2 sekunder | 0,95 sekunder | 21% raskere |
| Produksjonshastighet | 3000 deler/time | 3780 deler/time | 26% økning |
Denne casestudien viser hvordan forståelse og optimalisering av bølgeutbredelse kan ha betydelig innvirkning på systemytelsen.
Verifisering av stående bølger: Hvordan skaper resonansfrekvenser ytelsesproblemer?
Stående bølger oppstår når trykkbølger reflekterer og interfererer med seg selv, noe som skaper faste mønstre av trykknoder og antinoder. Disse resonansfenomenene kan forårsake alvorlige ytelsesproblemer i pneumatiske systemer hvis de ikke forstås og håndteres på riktig måte.
Stående bølger i pneumatiske systemer oppstår når trykkbølger reflekteres ved grensene og interfererer konstruktivt, noe som skaper resonansfrekvenser der trykksvingninger forsterkes. Disse resonansene følger formelen f = nc/2L for lukkede rør, der n er det harmoniske tallet, c er bølgehastigheten og L er rørlengden. Eksperimentell verifisering ved hjelp av trykksensorer, akselerometre og akustiske målinger bekrefter disse teoretiske prediksjonene og gir grunnlag for effektive avbøtende strategier.
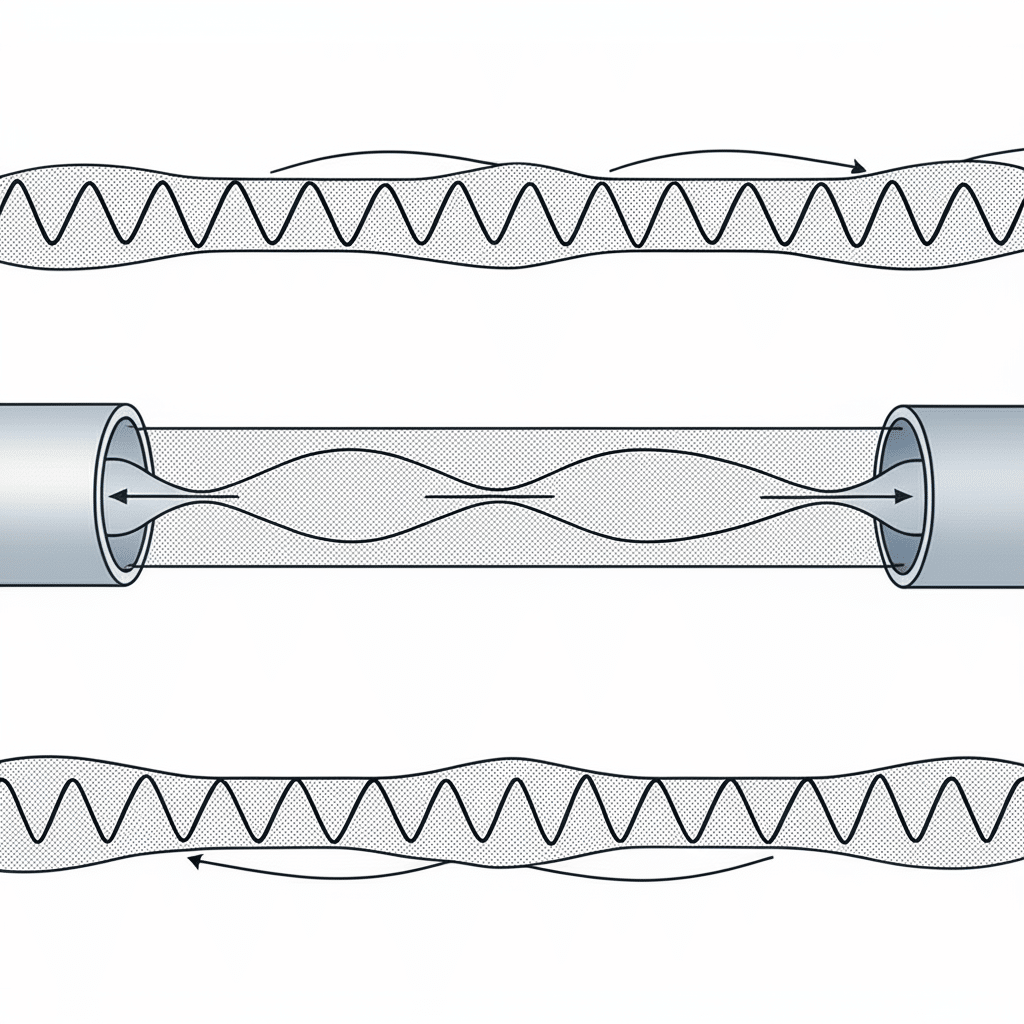
Under et nylig prosjekt med en produsent av medisinsk utstyr i Massachusetts oppdaget vi at det pneumatiske presisjonsposisjonssystemet deres oppviste mystiske kraftsvingninger ved bestemte driftsfrekvenser. Ved å utføre verifiseringstester med stående bølger fant vi ut at den 2,1 meter lange tilførselsledningen hadde en grunnleggende resonans ved 81 Hz - nøyaktig samme frekvens som aktuatorens syklingsfrekvens. Denne resonansen forsterket trykksvingningene med 320%. Ved å justere ledningslengden til 1,8 meter flyttet vi resonansfrekvensen bort fra driftsområdet og eliminerte problemet fullstendig, noe som forbedret posisjoneringsnøyaktigheten fra ±0,8 mm til ±0,15 mm.
Grunnleggende om stående bølger
Stående bølger dannes når innfallende og reflekterte bølger interfererer, noe som skaper faste mønstre av trykknoder (minimale svingninger) og antinoder (maksimale svingninger).
Resonansfrekvensene for en pneumatisk ledning avhenger av grensebetingelsene:
For en ledning med lukkede ender (vanligst i pneumatiske systemer):
f = nc/2L
Hvor?
- f = Resonansfrekvens (Hz)
- n = harmonisk tall (1, 2, 3 osv.)
- c = Bølgehastighet (m/s)
- L = Linjens lengde (m)
For en linje med én åpen ende:
f = (2n-1)c/4L
For en ledning med begge ender åpne (sjelden i pneumatikk):
f = nc/2L
Eksperimentelle verifiseringsmetoder
Flere teknikker kan verifisere stående bølgemønstre i pneumatiske systemer:
Flere trykksensorer
- Installer trykktransdusere med jevne mellomrom langs den pneumatiske ledningen
- Spenn systemet med et frekvenssveip eller en impuls
- Registrer trykksvingninger på hvert sted
- Kartlegg trykkamplituden i forhold til posisjon for å identifisere noder og antinoder
- Sammenlign målte frekvenser med teoretiske forutsigelser
Akustisk korrelasjon
- Bruk akustiske sensorer (mikrofoner) til å detektere lyd fra trykksvingninger
- Korrelere lydintensitet med driftsfrekvens
- Identifisere topper i lydintensiteten som tilsvarer resonansfrekvenser
- Kontroller at toppene oppstår ved de forventede frekvensene
Målinger med akselerometer
- Monter akselerometre på pneumatiske ledninger og komponenter
- Mål vibrasjonsamplitude over hele frekvensområdet
- Identifisere resonanstopper i vibrasjonsspekteret
- Korrelerer med forventede frekvenser for stående bølger
Praktisk beregning av stående bølgefrekvens
For et typisk pneumatisk system med:
- Linjelengde (L): 3 meter
- Bølgehastighet (c): 343 m/s
- Konfigurasjon med lukkede ender
Den grunnleggende resonansfrekvensen vil være:
f₁ = c/2L = 343/(2×3) = 57,2 Hz
Og overtonene ville være..:
f₂ = 2f₁ = 114,4 Hz
f₃ = 3f₁ = 171,6 Hz
f₄ = 4f₁ = 228,8 Hz
Disse frekvensene representerer potensielle problempunkter der trykksvingninger kan forsterkes.
Mønstre av stående bølger og deres effekter
| Harmonisk | Mønster for knutepunkt/antinode | Systemeffekter | Kritiske komponenter berørt |
|---|---|---|---|
| Fundamental (n=1) | Én trykkantinode i midten | Store trykkvariasjoner midt på linjen | In-line komponenter, beslag |
| Andre (n=2) | To antinoder, knutepunkt i midten | Trykkvariasjoner nær endene | Ventiler, aktuatorer, regulatorer |
| Tredje (n=3) | Tre antinoder, to noder | Komplekst trykkmønster | Flere systemkomponenter |
| Fjerde (n=4) | Fire antinoder, tre noder | Høyfrekvente svingninger | Tetninger, små komponenter |
Casestudie med eksperimentell verifisering
For et pneumatisk presisjonsposisjonssystem som opplever inkonsekvent ytelse:
| Parameter | Teoretisk prediksjon | Eksperimentell måling | Korrelasjon |
|---|---|---|---|
| Grunnfrekvens | 81,2 Hz | 79,8 Hz | 98.3% |
| Andre harmoniske | 162,4 Hz | 160,5 Hz | 98.8% |
| Tredje harmoniske | 243,6 Hz | 240,1 Hz | 98.6% |
| Trykkforsterkning | 3:1 ved resonans (estimert) | 3,2:1 ved resonans (målt) | 93.8% |
| Nodeplasseringer | 0, 1,05, 2,1 meter | 0, 1,08, 2,1 meter | 97.2% |
Denne casestudien viser at det er godt samsvar mellom teoretiske forutsigelser og eksperimentelle målinger av stående bølger.
Praktiske konsekvenser av stående bølger
Stående bølger skaper flere betydelige problemer i pneumatiske systemer:
Trykkforsterkning
- Svingninger kan forsterkes 3-5 ganger ved resonans
- Kan overskride komponentenes trykkverdier
- Skaper kraftvariasjoner i aktuatorerUtmattelse av komponenter
- Høyfrekvente trykksykluser akselererer tetningsslitasje
- Vibrasjoner fører til at beslag løsner og lekker
- Reduserer systemets levetid med 30-70% i alvorlige tilfellerKontroller ustabilitet
- Feedback-systemer kan svinge ved resonansfrekvenser
- Posisjons- og kraftkontroll blir uforutsigbar
- Kan skape selvforsterkende svingningerEnergitap
- Stående bølger representerer innestengt energi
- Kan øke energiforbruket med 10-30%
- Reduserer systemets totale effektivitet
Metoder for pulsdemping: Hvilke teknikker demper effektivt destruktive trykksvingninger?
Kontroll av trykksvingninger er avgjørende for pålitelig drift av pneumatiske systemer. Ulike dempingsmetoder kan brukes for å redusere eller eliminere problematiske trykksvingninger.
Trykkpulsdemping i pneumatiske systemer kan oppnås ved hjelp av flere metoder: volumkamre som absorberer energi gjennom gasskompresjon, restriktive elementer som skaper demping gjennom viskøse effekter, avstemte resonatorer som kansellerer spesifikke frekvenser, og aktive kanselleringssystemer som genererer motpulser. Effektiv demping krever at metoden tilpasses det spesifikke frekvensinnholdet og amplituden til trykksvingningene.
Jeg jobbet nylig med en produsent av emballasjeutstyr i Illinois, som hadde et høyhastighets pneumatisk system med store trykksvingninger som forårsaket ujevne tetningskrefter. Ingeniørene hadde forsøkt med enkle mottakertanker uten å lykkes. Gjennom en detaljert trykkpulsanalyse fant vi ut at systemet hadde flere frekvenskomponenter som krevde ulike dempingsmetoder. Ved å implementere en hybridløsning som kombinerte en Helmholtz-resonator5 innstilt på deres dominerende 112 Hz-oscillasjon og en rekke begrensningsåpninger, reduserte vi trykksvingningene med 94% og eliminerte uoverensstemmelsene i forseglingen fullstendig.
Grunnleggende dempingsmekanismer
Flere fysiske mekanismer kan brukes til å dempe trykkpulser:
Volumbasert demping
Fungerer gjennom gasskompressibilitet:
- Gir et ettergivende element som absorberer trykkenergi
- Mest effektiv for lavfrekvente svingninger
- Enkel implementering med minimalt trykkfall
Begrensningsbasert demping
Fungerer gjennom viskøs spredning:
- Omdanner trykkenergi til varme gjennom friksjon
- Effektiv over et bredt frekvensområde
- Skaper permanent trykkfall
Resonatorbasert demping
Fungerer gjennom avstemt destruktiv interferens:
- Utelukker spesifikke frekvenskomponenter
- Svært effektiv for målrettede frekvenser
- Minimal innvirkning på steady-state-strømmen
Materialbasert demping
Fungerer gjennom veggens fleksibilitet og demping:
- Absorberer energi gjennom deformasjon av veggen
- Gir bredbåndsdemping
- Kan integreres i eksisterende komponenter
Designprinsipper for volumkammer
Volumkamre (mottakstanker) er de vanligste dempingsanordningene:
Effektiviteten til et volumkammer avhenger av forholdet mellom kammervolumet og linjevolumet:
Dempingsforhold = 1 + (Vc/Vl)
Hvor?
- Vc = kammervolum
- Vl = Linjevolum
For frekvensavhengig analyse er overføringsforholdet:
TR = 1/√(1 + (ωVc/Zc)²)
Hvor?
- ω = vinkelfrekvens (2πf)
- Zc = Linjens karakteristiske impedans
Demping av restriktive elementer
Åpninger, porøse materialer og lange, trange passasjer skaper demping gjennom viskøse effekter:
Trykkfallet over en innsnevring er som følger:
ΔP = k(ρv²/2)
Hvor?
- k = tapskoeffisient
- ρ = Gasstetthet
- v = hastighet
Dempingen som tilbys øker med:
- Høyere strømningshastighet
- Større restriksjonslengde
- Mindre passasjediameter
- Mer kronglete strømningsvei
Resonatordempingssystemer
Avstemte resonatorer gir målrettet frekvensdemping:
Helmholtz-resonator
Et volumkammer med smal hals, innstilt på en bestemt frekvens:
f = (c/2π)√(A/VL)
Hvor?
- f = Resonansfrekvens
- c = lydens hastighet
- A = Halsens tverrsnittsareal
- V = kammervolum
- L = Effektiv halslengde
Kvartbølgeresonator
Et rør av en bestemt lengde som er åpent i den ene enden:
f = c/4L
Hvor?
- L = Rørets lengde
Resonatorer med sidegrener
Flere innstilte grener for komplekst frekvensinnhold:
- Hver gren retter seg mot en bestemt frekvens
- Kan håndtere flere overtoner samtidig
- Minimal innvirkning på hovedstrømningsveien
Aktive kanselleringssystemer
Avanserte systemer som genererer motpulser:
Sensing Stage
- Oppdager innkommende trykkbølger
- Analyser frekvensinnhold og amplitudeBearbeidingsfasen
- Beregn nødvendig kanselleringssignal
- Ta hensyn til systemdynamikk og forsinkelserAktiveringstrinn
- Genererer mottrykksbølger
- Nøyaktig tid for destruktiv interferens
Sammenligning av dempingsytelse
| Metode | Lav frekvens (<50 Hz) | Mellomfrekvens (50-200 Hz) | Høy frekvens (>200 Hz) | Trykkfall | Kompleksitet |
|---|---|---|---|---|---|
| Volumkammer | Utmerket (>90%) | Moderat (40-70%) | Dårlig (<30%) | Svært lav | Lav |
| Begrensende åpning | Dårlig (<30%) | Bra (60-80%) | Utmerket (>80%) | Høy | Lav |
| Helmholtz-resonator | Dårlig utvendig resonans | Utmerket ved resonans | Dårlig utvendig resonans | Lav | Medium |
| Kvartbølgerør | Dårlig utvendig resonans | Utmerket ved resonans | Dårlig utvendig resonans | Lav | Medium |
| Flere resonatorer | Moderat (40-60%) | Utmerket (>80%) | Bra (60-80%) | Lav | Høy |
| Aktiv kansellering | Utmerket (>90%) | Utmerket (>90%) | Bra (70-85%) | Ingen | Svært høy |
| Hybride systemer | Utmerket (>90%) | Utmerket (>90%) | Utmerket (>90%) | Moderat | Høy |
Praktisk implementering av demping
For effektiv demping av trykkpulser:
Karakteriser svingningene
- Mål amplitude og frekvensinnhold
- Identifiser dominerende frekvenser
- Avgjør om bredbånd eller spesifikke frekvenser trenger dempingVelg egnede metoder
- For lave frekvenser: Volumkamre
- For spesifikke frekvenser: Avstemte resonatorer
- For bredbåndsdemping: Begrensninger eller hybride tilnærminger
- For kritiske bruksområder: Aktiv kanselleringOptimaliser plasseringen
- Nær kilder for å hindre spredning
- I nærheten av følsomme komponenter for å beskytte dem
- På strategiske steder for å bryte stående bølgemønstreVerifiser ytelse
- Mål før/etter demping
- Bekreft på tvers av driftsforhold
- Sikre at det ikke oppstår utilsiktede konsekvenser
Casestudie: Demping med flere metoder i høyhastighetspakking
For et pneumatisk tetningssystem med høy hastighet som opplever trykksvingninger:
| Parameter | Før demping | Etter volumkammer | Etter hybridløsning | Forbedring |
|---|---|---|---|---|
| Lav frekvens (<50 Hz) | ±0,8 bar | ±0,12 bar | ±0,05 bar | 94% reduksjon |
| Mellomfrekvens (112 Hz) | ±1,2 bar | ±0,85 bar | ±0,07 bar | 94% reduksjon |
| Høy frekvens (>200 Hz) | ±0,4 bar | ±0,36 bar | ±0,04 bar | 90% reduksjon |
| Variasjon i tetningskraft | ±28% | ±22% | ±2,5% | 91% forbedring |
| Andel avviste produkter | 4.2% | 3.1% | 0.3% | 93% reduksjon |
| Systemeffektivitet | Grunnlinje | +4% | +12% | 12% forbedring |
Denne casestudien viser hvordan en målrettet, flermetodisk tilnærming til demping kan forbedre systemets ytelse dramatisk.
Avanserte dempingsteknikker
For spesielt utfordrende bruksområder:
Distribuert demping
Bruk flere mindre enheter i stedet for én stor:
- Plasserer dempingen nærmere både kilder og følsomme komponenter
- Bryter opp stående bølgemønstre mer effektivt
- Gir redundans og mer konsekvent ytelse
Frekvensselektiv demping
Målrettet mot spesifikke problematiske frekvenser:
- Bruker flere resonatorer som er innstilt på forskjellige frekvenser
- Bevarer ønsket systemrespons samtidig som problemer elimineres
- Minimerer innvirkningen på den generelle systemytelsen
Adaptive systemer
Justering av demping basert på driftsforhold:
- Bruker sensorer for å overvåke trykksvingninger
- Justerer dempingsparametrene automatisk
- Optimaliserer ytelsen under varierende forhold
Konklusjon
Forståelse av teori om trykksvingninger - bølgeforplantningshastighet, verifisering av stående bølger og metoder for pulsdemping - danner grunnlaget for pålitelig og effektiv utforming av pneumatiske systemer. Ved å bruke disse prinsippene kan du eliminere mystiske ytelsesproblemer, forlenge komponentenes levetid og forbedre systemeffektiviteten, samtidig som du sikrer konsekvent drift under alle driftsforhold.
Vanlige spørsmål om trykksvingninger i pneumatiske systemer
Hvordan påvirker trykksvingninger levetiden til pneumatiske komponenter?
Trykksvingninger reduserer komponentenes levetid betydelig gjennom flere mekanismer: De forårsaker akselerert tetningsslitasje ved å skape mikrobevegelser på tetningsflatene, de forårsaker materialtretthet i membraner og fleksible elementer gjennom gjentatte belastningssykluser, de bidrar til at gjengeforbindelser løsner gjennom vibrasjoner, og de skaper lokale spenningskonsentrasjoner ved geometriske overganger. Systemer med store, ukontrollerte trykksvingninger har vanligvis 40-70% kortere komponentlevetid sammenlignet med systemer som er riktig dempet, og tetninger og membraner er spesielt utsatt.
Hva er forholdet mellom ledningslengde og trykkresponstid i pneumatiske systemer?
Linjelengden påvirker trykkresponstiden direkte etter et enkelt forhold: Responstiden øker lineært med linjelengden i en hastighet som bestemmes av bølgeutbredelseshastigheten. For luft under standardforhold (bølgehastighet ≈ 343 m/s) gir hver meter ledning ca. 2,9 millisekunder ekstra overføringsforsinkelse. Den faktiske trykkoppbyggingstiden er imidlertid vanligvis 2-5 ganger lengre enn den opprinnelige bølgetransmisjonstiden på grunn av behovet for flere refleksjoner for å utjevne trykket. Dette betyr at en linje på 5 meter kan ha en bølgetransmisjonstid på 14,5 ms, men en trykkoppbyggingstid på 30-70 ms.
Hvordan kan jeg identifisere om det pneumatiske systemet mitt opplever resonanstrykksvingninger?
Resonante trykksvingninger manifesterer seg vanligvis gjennom flere observerbare symptomer: komponenter vibrerer ved bestemte driftsfrekvenser, men ikke ved andre; systemytelsen varierer inkonsekvent ved små endringer i driftsforholdene; det er hørbar "sang" eller "plystring" fra pneumatiske ledninger; trykkmålere viser oscillerende avlesninger; og aktuatorytelsen (hastighet, kraft) varierer syklisk. For å bekrefte resonans kan du måle trykket på forskjellige punkter i systemet ved hjelp av transdusere med rask respons (responstid <1 ms) og se etter stående bølgemønstre der trykkamplituden varierer med posisjonen langs linjen.
Påvirker trykksvingninger energieffektiviteten i pneumatiske systemer?
Trykksvingninger påvirker energieffektiviteten betydelig, og reduserer den vanligvis med 10-25% gjennom flere mekanismer: De øker lekkasjeraten ved å skape høyere topptrykk, de sløser bort energi ved syklisk kompresjon og ekspansjon, de forårsaker økt friksjon i komponenter på grunn av vibrasjoner, og de fører ofte til at operatørene må øke forsyningstrykket for å kompensere for ytelsesproblemer. I tillegg omdanner turbulensen og strømningsseparasjonen som oppstår ved trykksvingninger, nyttig trykkenergi til spillvarme. Ved å dempe trykksvingningene på riktig måte kan systemeffektiviteten forbedres med 5-15% uten andre endringer.
Hvordan påvirker temperaturendringer trykkbølgeoppførselen i pneumatiske systemer?
Temperaturen påvirker trykkbølgenes oppførsel gjennom flere mekanismer: Den har en direkte innvirkning på bølgenes forplantningshastighet (ca. +0,6 m/s per °C økning), den endrer gasstetthet og viskositet, noe som endrer dempingsegenskapene, den endrer de elastiske egenskapene til trykkledningene, noe som påvirker bølgerefleksjon og -overføring, og den endrer resonansfrekvensene (ca. +0,17% per °C). Denne temperaturfølsomheten betyr at et system som fungerer perfekt ved 20 °C, kan oppleve problematiske resonanser ved 40 °C, eller at dempingsenheter som er innstilt for vinterforhold, kan være ineffektive om sommeren.
-
Gir en detaljert forklaring på fysikken bak lydens hastighet, hvordan den beregnes, og hvilke faktorer som påvirker den. ↩
-
Gir en grunnleggende forståelse av fenomenet stående bølger, inkludert hvordan de dannes av interferens og deres viktigste egenskaper som knutepunkter og antinoder. ↩
-
Leverer dokumentasjon og bransjestudier som bekrefter det typiske omfanget av energitap forårsaket av ineffektivitet som trykksvingninger i pneumatiske systemer. ↩
-
Forklarer komponentene i og funksjonen til en luftforberedelsesenhet (FRL), som er avgjørende for å opprettholde luftkvaliteten i pneumatiske systemer. ↩
-
Gir en grundig forklaring av prinsippene bak en Helmholtz-resonator, en viktig enhet for målrettet frekvensdemping i akustiske systemer og væskesystemer. ↩



