Inżynierowie napotykają na pomyłki podczas obliczania objętości spłaszczonych elementów kulistych w beztłoczyskowych układach siłowników pneumatycznych. Nieprawidłowe obliczenia objętości prowadzą do błędnych obliczeń ciśnienia i awarii systemu.
Płaska kula (sferoida spłaszczona) ma objętość V = (4/3)πa²b, gdzie "a" to promień równikowy, a "b" to promień biegunowy, powszechnie spotykany w akumulator pneumatyczny1 i amortyzacji.
W zeszłym miesiącu pomogłem Andreasowi, inżynierowi projektantowi z Niemiec, którego pneumatyczny system amortyzacji zawiódł, ponieważ użył standardowej objętości kuli zamiast obliczeń sferoidy spłaszczonej dla swoich spłaszczonych komór akumulatorowych.
Spis treści
- Czym jest płaska kula w zastosowaniach pneumatycznych?
- Jak obliczyć objętość płaskiej kuli?
- Gdzie stosuje się płaskie kule w siłownikach beztłoczyskowych?
- Jak spłaszczenie wpływa na objętość i wydajność?
Czym jest płaska kula w zastosowaniach pneumatycznych?
Płaska kula, technicznie nazywana spłaszczona sferoida2jest trójwymiarowym kształtem tworzonym, gdy kula jest ściskana wzdłuż jednej osi, powszechnie stosowanym w projektach akumulatorów pneumatycznych i amortyzacji.
Płaska kula powstaje w wyniku spłaszczenia idealnej kuli wzdłuż jej osi pionowej, tworząc eliptyczny przekrój o różnych wymiarach promieni poziomych i pionowych.
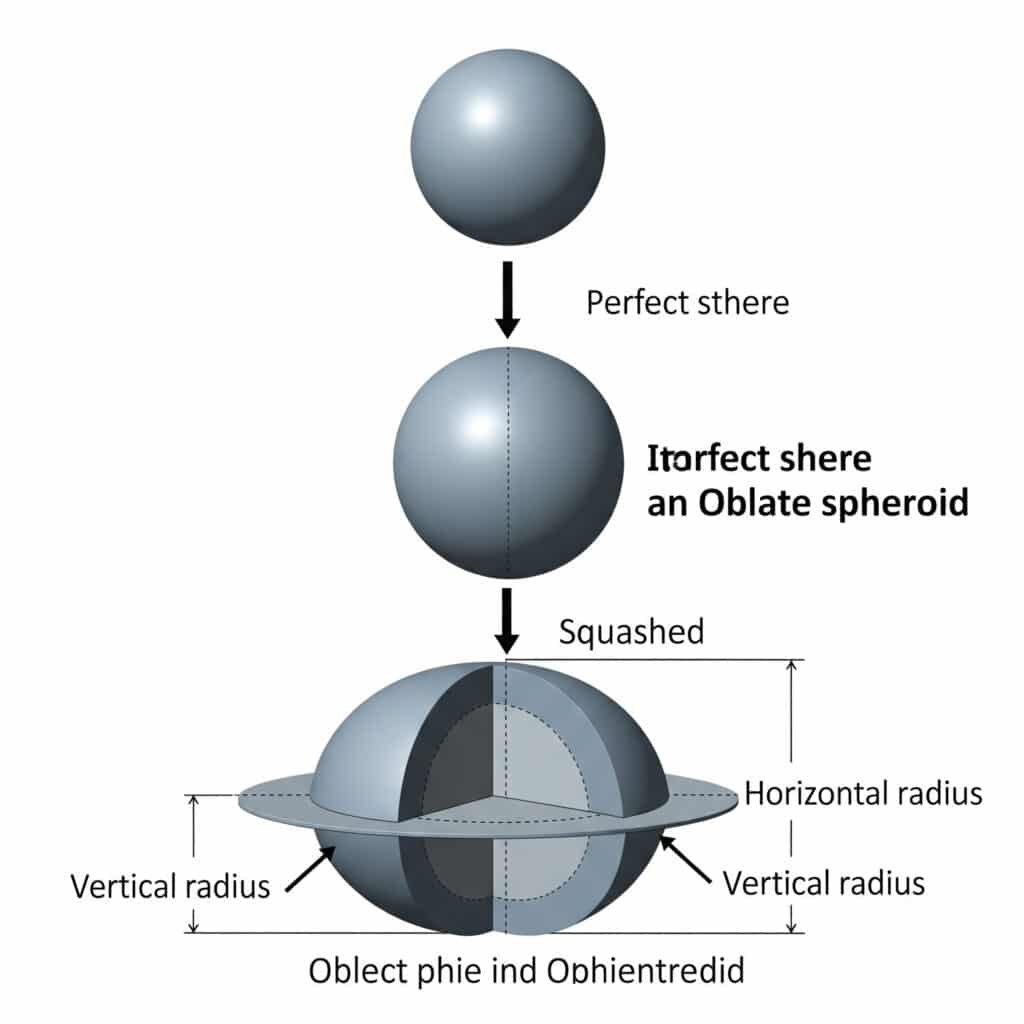
Definicja geometryczna
Charakterystyka kształtu
- Sferoida spłaszczona: Techniczny termin geometryczny
- Spłaszczona kula: Wspólny opis przemysłowy
- Profil eliptyczny: Widok przekroju poprzecznego
- Symetria obrotowa: Wokół osi pionowej
Kluczowe wymiary
- Promień równikowy (a): Promień poziomy (większy)
- Promień biegunowy (b): Promień pionowy (mniejszy)
- Współczynnik spłaszczeniab/a < 1,0
- Współczynnik kształtu: Stosunek wysokości do szerokości
Kula płaska vs kula idealna
| Charakterystyka | Perfect Sphere | Płaska kula |
|---|---|---|
| Kształt | Jednolity promień | Kompresja pionowa |
| Wzór na objętość | (4/3)πr³ | (4/3)πa²b |
| Przekrój | Koło | Elipsa |
| Symetria | Wszystkie kierunki | Tylko w poziomie |
Typowe współczynniki spłaszczenia
Lekkie spłaszczenie
- Stosunekb/a = 0,8-0,9
- Zastosowania: Niewielkie ograniczenia przestrzeni
- Wpływ wolumenu: 10-20% redukcja
- Wydajność: Minimalny efekt
Umiarkowane spłaszczenie
- Stosunekb/a = 0,6-0,8
- Zastosowania: Standardowe konstrukcje akumulatorów
- Wpływ wolumenuRedukcja 20-40%
- Wydajność: Zauważalne zmiany ciśnienia
Mocne spłaszczenie
- Stosunekb/a = 0,3-0,6
- Zastosowania: Poważne ograniczenia przestrzeni
- Wpływ wolumenu: 40-70% redukcja
- Wydajność: Istotne kwestie projektowe
Zastosowania pneumatyczne
Komory akumulatorów
Spotykam się z płaskimi kulami:
- Instalacje o ograniczonej przestrzeni: Ograniczenia wysokości
- Zintegrowane projekty: Wbudowane w ramy maszyn
- Aplikacje niestandardowe: Specyficzne wymagania dotyczące objętości
- Projekty modernizacji: Dopasowanie do istniejących przestrzeni
Systemy amortyzacji
- Tłumienie końca skoku: Zastosowania siłowników beztłoczyskowych
- Pochłanianie wstrząsów: Zarządzanie obciążeniem udarowym
- Regulacja ciśnienia: Płynna kontrola działania
- Redukcja hałasu: Cichsza praca systemu
Rozważania dotyczące produkcji
Metody produkcji
- Głębokie rysowanie: Formowanie blachy
- Hydroformowanie: Precyzyjny proces kształtowania
- Obróbka skrawaniem: Niestandardowe komponenty jednorazowe
- Casting: Produkcja wielkoseryjna
Wybór materiału
- Stal: Zastosowania wysokociśnieniowe
- Aluminium: Konstrukcje wrażliwe na wagę
- Stal nierdzewna: Środowiska korozyjne
- Materiały kompozytowe: Specjalistyczne wymagania
Jak obliczyć objętość płaskiej kuli?
Obliczenie objętości płaskiej kuli wymaga zastosowania wzoru na sferoidę spłaszczoną z wykorzystaniem pomiarów zarówno promienia równikowego, jak i biegunowego w celu dokładnego zaprojektowania układu pneumatycznego.
Użyj wzoru V = (4/3)πa²b, gdzie "a" to promień równikowy (poziomy), a "b" to promień biegunowy (pionowy), aby dokładnie obliczyć objętość płaskiej kuli.
Podział formuły wolumenu
Standardowa formuła
V = (4/3)πa²b
- V: Objętość w jednostkach sześciennych
- π: 3.14159 (stała matematyczna)
- a: Promień równikowy (poziomy)
- b: Promień biegunowy (pionowy)
- 4/3: Współczynnik objętości sferoidy
Składniki formuły
- Obszar równikowyπa² (przekrój poziomy)
- Skalowanie biegunoweWspółczynnik b (kompresja pionowa)
- Współczynnik objętości: 4/3 (stała geometryczna)
- Jednostki wyników: Dopasowany promień wejściowy w jednostkach sześciennych
Obliczenia krok po kroku
Proces pomiaru
- Pomiar średnicy równikowej: Najszerszy wymiar poziomy
- Obliczyć promień równikowya = średnica ÷ 2
- Pomiar średnicy biegunowej: Pionowy wymiar wysokości
- Obliczyć promień biegunowyb = wysokość ÷ 2
- Zastosuj formułę: V = (4/3)πa²b
Przykład obliczeń
Dla akumulatora pneumatycznego:
- Średnica równikowa: 100mm → a = 50mm
- Średnica biegunowa60 mm → b = 30 mm
- Objętość: V = (4/3)π(50)²(30)
- Wynik: V = (4/3)π(2500)(30) = 314,159 mm³
Przykłady obliczania objętości
| Promień równikowy | Promień biegunowy | Współczynnik spłaszczenia | Objętość | Porównanie do Sphere |
|---|---|---|---|---|
| 50 mm | 50 mm | 1.0 | 523 599 mm³ | 100% (idealna kula) |
| 50 mm | 40 mm | 0.8 | 418,879 mm³ | 80% |
| 50 mm | 30 mm | 0.6 | 314,159 mm³ | 60% |
| 50 mm | 20 mm | 0.4 | 209 440 mm³ | 40% |
Narzędzia obliczeniowe
Obliczenia ręczne
- Kalkulator naukowy: Z funkcją π
- Weryfikacja formuły: Podwójna kontrola danych wejściowych
- Spójność jednostki: Utrzymywanie tych samych jednostek przez cały czas
- Precyzja: Obliczanie z odpowiednimi miejscami dziesiętnymi
Narzędzia cyfrowe
- Oprogramowanie inżynieryjne: Obliczenia objętości CAD
- Kalkulatory online: Narzędzia sferoidalne
- Formuły arkusza kalkulacyjnego: Zautomatyzowane obliczenia
- Aplikacje mobilne: Narzędzia do obliczeń w terenie
Typowe błędy obliczeniowe
Błędy pomiarowe
- Promień a średnica: Użycie niewłaściwego wymiaru
- Zamieszanie wokół osi: Mieszanie pomiarów poziomych i pionowych
- Niespójność jednostkimm vs mieszanie w calach
- Utrata precyzji: Zbyt wczesne zaokrąglanie
Błędy formuły
- Nieprawidłowa formuła: Używanie sfery zamiast sferoidy
- Odwrócenie parametrów: Zamiana wartości a i b
- Błędy współczynnika: Brakujący współczynnik 4/3
- π przybliżenie: Używanie 3.14 zamiast 3.14159
Metody weryfikacji
Techniki kontroli krzyżowej
- Oprogramowanie CAD: Obliczanie objętości modelu 3D
- Wyporność wody: Fizyczny pomiar objętości
- Wiele obliczeń: Porównanie różnych metod
- Specyfikacje producenta: Opublikowane dane dotyczące wolumenu
Kontrola zasadności
- Redukcja objętości: Powinna być mniej niż idealna kula
- Spłaszczenie korelacji: Większe spłaszczenie = mniejsza objętość
- Weryfikacja jednostki: Wyniki odpowiadają oczekiwanej wielkości
- Przydatność aplikacji: Wolumin spełnia wymagania systemowe
Kiedy pomogłem Marii, projektantce systemów pneumatycznych z Hiszpanii, obliczyć objętość akumulatora dla jej instalacji z siłownikiem beztłoczyskowym, odkryliśmy, że w jej oryginalnych obliczeniach użyto wzorów sferycznych zamiast sferoidalnych, co spowodowało przeszacowanie objętości 35% i nieodpowiednią wydajność systemu.
Gdzie stosuje się płaskie kule w siłownikach beztłoczyskowych?
Płaskie kule pojawiają się w różnych komponentach beztłoczyskowych siłowników pneumatycznych, gdzie ograniczenia przestrzenne wymagają optymalizacji objętości przy jednoczesnym zachowaniu funkcjonalności zbiornika ciśnieniowego.
Płaskie kule są powszechnie stosowane w komorach akumulatorów, systemach amortyzacji i zintegrowanych zbiornikach ciśnieniowych w beztłoczyskowych zespołach cylindrów, gdzie ograniczenia wysokości ograniczają standardowe konstrukcje kuliste.
Zastosowania akumulatorów
Zintegrowane akumulatory
- Optymalizacja przestrzeni: Dopasowanie do ram maszyn
- Wydajność objętościowa: Maksymalna pojemność przy ograniczonej wysokości
- Stabilność ciśnienia: Płynne działanie podczas szczytów zapotrzebowania
- Integracja systemu: Wbudowany w podstawę montażową cylindra
Instalacje modernizacyjne
- Istniejące maszyny: Ograniczenia wysokości
- Projekty modernizacji: Dodawanie akumulacji do starszych systemów
- Ograniczenia przestrzenne: Praca w ramach oryginalnego projektu
- Poprawa wydajności: Ulepszona reakcja systemu
Systemy amortyzacji
Tłumienie końca suwu
Montuję płaską amortyzację kulistą:
- Magnetyczne cylindry beztłoczyskowe: Płynne zwalnianie
- Prowadzone cylindry beztłoczyskowe: Redukcja wpływu
- Siłowniki beztłoczyskowe dwustronnego działania: Dwukierunkowa amortyzacja
- Szybkie aplikacje: Pochłanianie wstrząsów
Regulacja ciśnienia
- Wygładzanie przepływu: Eliminacja skoków ciśnienia
- Redukcja hałasu: Cichsza praca
- Ochrona podzespołów: Zmniejszone zużycie i naprężenia
- Stabilność systemu: Stała wydajność
Komponenty specjalistyczne
Zbiorniki ciśnieniowe
- Aplikacje niestandardowe: Wyjątkowe wymagania przestrzenne
- Konstrukcje wielofunkcyjne: Połączone przechowywanie i montaż
- Systemy modułowe: Konfiguracje z możliwością układania w stosy
- Dostęp serwisowy: Projekty nadające się do użytku
Komory czujników
- Monitorowanie ciśnienia: Zintegrowane systemy pomiarowe
- Wykrywanie przepływu: Aplikacje do wykrywania prędkości
- Diagnostyka systemu: Monitorowanie wydajności
- Systemy bezpieczeństwa: Zintegrowana redukcja ciśnienia
Rozważania projektowe
Ograniczenia przestrzenne
| Zastosowanie | Limit wysokości | Typowe spłaszczenie | Wpływ wolumenu |
|---|---|---|---|
| Montaż pod podłogą | 50 mm | b/a = 0,3 | Redukcja 70% |
| Integracja maszyn | 100 mm | b/a = 0,6 | Redukcja 40% |
| Zastosowania modernizacyjne | 150 mm | b/a = 0,8 | Redukcja 20% |
| Montaż standardowy | 200 mm+ | b/a = 0,9 | 10% redukcja |
Wymagania dotyczące wydajności
- Ciśnienie znamionowe: Utrzymanie integralności strukturalnej
- Pojemność: Spełnienie wymagań systemu
- Charakterystyka przepływu: Odpowiedni rozmiar wlotu/wylotu
- Dostęp serwisowy: Kwestie związane z serwisowaniem
Przykłady instalacji
Maszyny pakujące
- Zastosowanie: Szybki sprzęt do napełniania
- Ograniczenie: Prześwit 40 mm
- Rozwiązanie: Mocno spłaszczony akumulator (b/a = 0,25)
- Wynik75% redukcja głośności, odpowiednia wydajność
Montaż w branży motoryzacyjnej
- Zastosowanie: Zrobotyzowany system pozycjonowania
- Ograniczenie: Integracja z bazą robotów
- Rozwiązanie: Umiarkowane spłaszczenie (b/a = 0,7)
- Wynik: 30% oszczędność miejsca, utrzymana wydajność
Przetwarzanie żywności
- Zastosowanie: Sanitarny system beztłoczyskowy
- Ograniczenie: Dopuszczalne środowisko zmywania
- Rozwiązanie: Niestandardowy projekt płaskiej kuli
- Wynik: Stopień ochrony IP69K3 ze zoptymalizowaną głośnością
Specyfikacje produkcyjne
Standardowe rozmiary
- Mały: 50 mm równikowe, różne wymiary biegunowe
- Średni: 100 mm równikowe, zmiany wysokości
- Duży200 mm równikowy, niestandardowy rozmiar biegunowy
- Niestandardowe: Wymiary specyficzne dla aplikacji
Opcje materiałowe
- Stal węglowa: Standardowe aplikacje ciśnieniowe
- Stal nierdzewna: Środowiska korozyjne
- Aluminium: Instalacje wrażliwe na ciężar
- Kompozyt: Specjalistyczne wymagania
W zeszłym roku współpracowałem z Thomasem, konstruktorem maszyn ze Szwajcarii, który potrzebował akumulatorów do swojej kompaktowej linii pakującej. Standardowe akumulatory sferyczne nie zmieściłyby się w ograniczeniu wysokości 60 mm, więc zaprojektowaliśmy płaskie akumulatory sferyczne o stosunku b/a = 0,4, uzyskując 60% pierwotnej objętości przy jednoczesnym spełnieniu wszystkich ograniczeń przestrzennych.
Jak spłaszczenie wpływa na objętość i wydajność?
Spłaszczenie znacznie zmniejsza pojemność, jednocześnie wpływając na dynamikę ciśnienia, charakterystykę przepływu i ogólną wydajność systemu w beztłoczyskowych zastosowaniach pneumatycznych.
Każdy wzrost spłaszczenia o 10% (spadek stosunku b/a) zmniejsza objętość o około 10% i wpływa na reakcję na ciśnienie, wzorce przepływu i wydajność systemu w zastosowaniach akumulatorów pneumatycznych.
Analiza wpływu wolumenu
Relacje redukcji objętości
Stosunek objętości = (b/a) dla sferoid spłaszczonych
- Zależność liniowa: Objętość zmniejsza się proporcjonalnie do spłaszczenia
- Przewidywalny wpływ: Łatwe obliczanie zmian objętości
- Elastyczność projektowania: Wybór optymalnego współczynnika spłaszczenia
- Kompromisy w zakresie wydajności: Równowaga między przestrzenią a pojemnością
Ilościowe zmiany objętości
| Współczynnik spłaszczenia (b/a) | Retencja objętości | Utrata objętości | Przydatność aplikacji |
|---|---|---|---|
| 0.9 | 90% | 10% | Doskonały |
| 0.8 | 80% | 20% | Bardzo dobry |
| 0.7 | 70% | 30% | Dobry |
| 0.6 | 60% | 40% | Uczciwy |
| 0.5 | 50% | 50% | Słaby |
| 0.4 | 40% | 60% | Bardzo słaby |
Wpływ ciśnienia na wydajność
Charakterystyka reakcji na ciśnienie
- Zmniejszona objętość: Szybsze zmiany ciśnienia
- Wyższa czułość: Lepsza reakcja na zmiany przepływu
- Zwiększona jazda na rowerze: Częstsze cykle ładowania/rozładowania
- Niestabilność systemu: Potencjalne oscylacje ciśnienia
Korekty obliczeń ciśnienia
P₁V₁ = P₂V₂ (Prawo Boyle'a4 dotyczy)
- Mniejsza objętość: Wyższe ciśnienie dla tej samej masy powietrza
- Wahania ciśnienia: Większe wahania podczas pracy
- Rozmiar systemu: Kompensacja większą wydajnością sprężarki
- Marginesy bezpieczeństwa: Zwiększone wymagania dotyczące ciśnienia znamionowego
Charakterystyka przepływu
Zmiany wzorca przepływu
- Wzrost turbulencji: Spłaszczony kształt powoduje zakłócenia przepływu
- Spadek ciśnienia: Wyższy opór dzięki zdeformowanym komorom
- Efekty wlotu/wylotu: Pozycjonowanie portu staje się krytyczne
- Prędkość przepływu: Zwiększona prędkość na odcinkach o ograniczonym dostępie
Wpływ natężenia przepływu
- Zmniejszony obszar efektywny: Ograniczenia przepływu
- Straty ciśnienia: Spadek efektywności energetycznej
- Czas reakcji: Wolniejsze tempo napełniania/rozładowywania
- Wydajność systemu: Ogólna redukcja wydajności
Rozważania strukturalne
Rozkład naprężeń
- Skoncentrowane naprężenia: Wyższe obciążenia w spłaszczonych obszarach
- Grubość materiału: Może wymagać wzmocnienia
- Odporność na zmęczenie5: Zmniejszony potencjał cyklu życia
- Czynniki bezpieczeństwa: Potrzebne większe marginesy projektowe
Wpływ ciśnienia znamionowego
| Współczynnik spłaszczenia | Wzrost stresu | Zalecany współczynnik bezpieczeństwa | Grubość materiału |
|---|---|---|---|
| 0.9 | 10% | 1.5 | Standard |
| 0.8 | 25% | 1.8 | +10% |
| 0.7 | 45% | 2.0 | +20% |
| 0.6 | 70% | 2.5 | +35% |
Optymalizacja wydajności systemu
Strategie wynagrodzeń
- Zwiększona ilość akumulatorów: Wiele mniejszych jednostek
- Praca pod wyższym ciśnieniem: Kompensacja utraty objętości
- Ulepszona konstrukcja przepływu: Optymalizacja konfiguracji wlotu/wylotu
- Strojenie systemu: Regulacja parametrów sterowania
Monitorowanie wydajności
- Częstotliwość cykli ciśnieniowych: Monitorowanie stabilności systemu
- Pomiary natężenia przepływu: Sprawdzić odpowiednią pojemność
- Wpływ temperatury: Sprawdzić pod kątem nadmiernego nagrzewania
- Częstotliwość konserwacji: Dostosuj na podstawie wyników
Wytyczne projektowe
Optymalny wybór spłaszczenia
- b/a > 0,8: Minimalny wpływ na wydajność
- b/a = 0,6-0,8: Dopuszczalne dla większości zastosowań
- b/a = 0,4-0,6: Wymaga starannego zaprojektowania systemu
- b/a < 0,4: Ogólnie niezalecane
Zalecenia dotyczące konkretnych zastosowań
- Jazda na rowerze z wysoką częstotliwością: Minimalizacja spłaszczenia (b/a > 0,7)
- Instalacje o krytycznym znaczeniu dla przestrzeni kosmicznej: Zaakceptuj kompromisy w zakresie wydajności
- Systemy o krytycznym znaczeniu dla bezpieczeństwa: Konserwatywne współczynniki spłaszczenia
- Projekty wrażliwe na koszty: Równowaga między wydajnością a oszczędnością miejsca
Dane dotyczące wydajności w świecie rzeczywistym
Wyniki studium przypadku
Kiedy przeanalizowałem dane dotyczące wydajności z 50 instalacji o różnych współczynnikach spłaszczenia:
- 10% spłaszczenie: Niewielki wpływ na wydajność
- 30% spłaszczenie: 15% wzrost częstotliwości jazdy na rowerze
- 50% spłaszczenie: 40% zmniejszenie efektywnej pojemności
- 70% spłaszczenie: Niestabilność systemu w 60% przypadków
Sukces optymalizacji
Dla Eleny, integratora systemów z Włoch, zoptymalizowaliśmy jej projekt beztłoczyskowego akumulatora cylindrycznego, ograniczając spłaszczenie do b/a = 0,75, uzyskując 25% oszczędności miejsca przy zachowaniu 95% pierwotnej wydajności systemu i eliminując problemy z niestabilnością ciśnienia.
Wnioski
Objętość płaskiej kuli wykorzystuje wzór V = (4/3)πa²b z promieniem równikowym "a" i promieniem biegunowym "b". Spłaszczenie proporcjonalnie zmniejsza objętość, ale wpływa na reakcję na ciśnienie i charakterystykę przepływu w zastosowaniach pneumatycznych.
Najczęściej zadawane pytania dotyczące objętości płaskiej sfery
Jaki jest wzór na objętość płaskiej kuli?
Wzór na objętość kuli płaskiej (sferoidy obłej) to V = (4/3)πa²b, gdzie "a" to promień równikowy (poziomy), a "b" to promień biegunowy (pionowy). Różni się to od wzoru na idealną sferę V = (4/3)πr³.
Ile objętości traci się podczas spłaszczania kuli?
Utrata objętości jest równa współczynnikowi spłaszczenia. Jeśli promień biegunowy wynosi 70% promienia równikowego (b/a = 0,7), objętość staje się 70% pierwotnej objętości kuli, co oznacza zmniejszenie objętości o 30%.
Gdzie stosuje się płaskie kule w układach pneumatycznych?
Płaskie sfery są stosowane w komorach akumulatorów, systemach amortyzacji i zbiornikach ciśnieniowych, w których ograniczenia wysokości ograniczają standardowe konstrukcje sferyczne. Typowe zastosowania obejmują integrację maszyn o ograniczonej przestrzeni i instalacje modernizacyjne.
Jak spłaszczenie wpływa na wydajność układu pneumatycznego?
Spłaszczenie zmniejsza pojemność, zwiększa wrażliwość na ciśnienie i powoduje turbulencje przepływu. Systemy z mocno spłaszczonymi akumulatorami (b/a < 0,6) mogą doświadczać niestabilności ciśnienia i zmniejszonej wydajności wymagającej kompensacji projektowej.
Jaki jest maksymalny zalecany współczynnik spłaszczenia?
W przypadku zastosowań pneumatycznych należy utrzymywać współczynniki spłaszczenia powyżej b/a = 0,6, aby uzyskać akceptowalną wydajność. Współczynniki poniżej 0,4 generalnie powodują niestabilność systemu i wymagają znacznych modyfikacji projektu w celu utrzymania odpowiedniego działania.
-
Zrozumienie funkcji i przeznaczenia akumulatorów pneumatycznych w systemach zasilania płynami. ↩
-
Poznaj definicję matematyczną i właściwości geometryczne sferoidy obłej. ↩
-
Zobacz oficjalną definicję i wymagania testowe dla stopnia ochrony IP69K. ↩
-
Zapoznaj się z zasadami prawa Boyle'a, które opisuje zależność między ciśnieniem a objętością gazu. ↩
-
Zapoznanie się z koncepcją odporności zmęczeniowej i zachowaniem materiałów pod wpływem cyklicznych obciążeń. ↩



