
Czy kiedykolwiek zauważyłeś tajemnicze wibracje w swoich przewodach pneumatycznych? Albo niewyjaśnione zmiany siły w siłownikach pomimo stabilnego ciśnienia zasilania? Zjawiska te nie są przypadkowe - są wynikiem fal ciśnienia rozchodzących się w systemie, powodując efekty, które mogą wahać się od drobnych nieefektywności do katastrofalnych awarii.
Wahania ciśnienia w układach pneumatycznych są zjawiskami falowymi, które rozchodzą się z prędkościami zbliżonymi do prędkość dźwięku1tworząc dynamiczne efekty, w tym rezonans, fale stojące2i wzmocnienie ciśnienia. Zrozumienie tych wahań ma kluczowe znaczenie, ponieważ mogą one powodować zmęczenie podzespołów, niestabilność sterowania oraz straty energii 10-25% w typowych systemach przemysłowych3.
W zeszłym miesiącu konsultowałem się z zakładem montażu samochodów w Tennessee, gdzie krytyczny pneumatyczny system mocowania doświadczał przerywanych wahań siły pomimo stabilnego ciśnienia zasilania. Ich zespół konserwacyjny wymienił zawory, regulatory, a nawet cały układ pneumatyczny. jednostka przygotowania powietrza4 bez powodzenia. Analizując dynamikę fal ciśnieniowych - w szczególności wzorce fal stojących w ich liniach zasilających - zidentyfikowaliśmy, że działały one z częstotliwością, która powodowała destrukcyjne zakłócenia w cylindrze. Proste dostosowanie długości linii wyeliminowało problem i zaoszczędziło tygodni opóźnień w produkcji. Pozwól, że pokażę Ci, jak zrozumienie teorii wahań ciśnienia może zmienić niezawodność Twojego systemu pneumatycznego.
Spis treści
- Prędkość propagacji fal: Jak szybko zaburzenia ciśnienia przemieszczają się w systemie?
- Weryfikacja fali stojącej: W jaki sposób częstotliwości rezonansowe powodują problemy z wydajnością?
- Metody tłumienia impulsów: Jakie techniki skutecznie tłumią destrukcyjne oscylacje ciśnienia?
- Wnioski
- Najczęściej zadawane pytania dotyczące wahań ciśnienia w układach pneumatycznych
Prędkość propagacji fal: Jak szybko zaburzenia ciśnienia przemieszczają się w systemie?
Zrozumienie, jak szybko zakłócenia ciśnienia rozprzestrzeniają się w układach pneumatycznych, ma fundamentalne znaczenie dla przewidywania i kontrolowania ich skutków. Prędkość propagacji określa czas reakcji systemu, częstotliwości rezonansowe i potencjał destrukcyjnych zakłóceń.
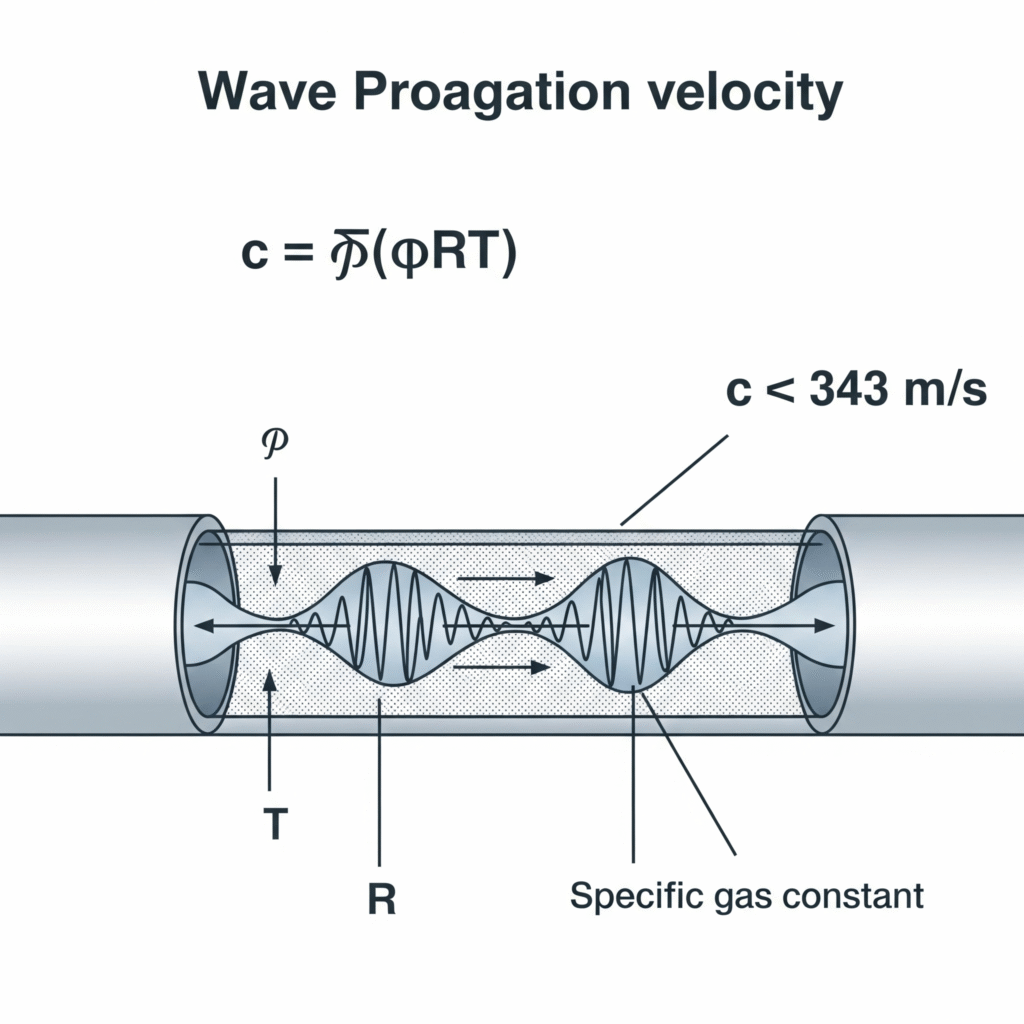
Fale ciśnienia w systemach pneumatycznych przemieszczają się z prędkością dźwięku w ośrodku gazowym, którą można obliczyć za pomocą wzoru c = √(γRT), gdzie γ to współczynnik ciepła właściwego, R to stała gazowa, a T to temperatura bezwzględna. Dla powietrza o temperaturze 20°C odpowiada to około 343 m/s, choć prędkość ta jest modyfikowana przez czynniki takie jak elastyczność rury, ściśliwość gazu i warunki przepływu.
Niedawno pomagałem w rozwiązywaniu problemów z precyzyjną maszyną montażową w Szwajcarii, gdzie chwytaki pneumatyczne doświadczały opóźnienia 12 ms między aktywacją a przyłożeniem siły - wieczność w szybkim środowisku produkcyjnym. Inżynierowie zakładali natychmiastową transmisję ciśnienia. Mierząc rzeczywistą prędkość propagacji fali w ich systemie (328 m/s) i uwzględniając 4-metrową długość linii, obliczyliśmy teoretyczny czas transmisji wynoszący 12,2 ms - prawie dokładnie odpowiadający zaobserwowanemu opóźnieniu. Przeniesienie zaworów bliżej siłowników zmniejszyło to opóźnienie do 3 ms i zwiększyło szybkość produkcji o 14%.
Podstawowe równania prędkości fali
Podstawowe równanie prędkości propagacji fali ciśnienia w gazie to:
c = √(γRT)
Gdzie:
- c = Prędkość propagacji fali (m/s)
- γ = Współczynnik ciepła właściwego (1,4 dla powietrza)
- R = Stała gazowa właściwa (287 J/kg-K dla powietrza)
- T = temperatura bezwzględna (K)
Dla powietrza o temperaturze 20°C (293K) daje to:
c = √(1,4 × 287 × 293) = 343 m/s
Zmodyfikowana prędkość fali w liniach pneumatycznych
W rzeczywistych systemach pneumatycznych efektywna prędkość fali jest modyfikowana przez elastyczność rury i inne czynniki zgodnie ze wzorem:
c_eff = c / √(1 + (Dψ/Eh))
Gdzie:
- c_eff = efektywna prędkość fali (m/s)
- D = średnica rury (m)
- ψ = Współczynnik ściśliwości gazu
- E = moduł sprężystości materiału rury (Pa)
- h = Grubość ścianki rury (m)
Wpływ temperatury i ciśnienia na prędkość fali
Prędkość fali zmienia się w zależności od warunków pracy:
| Temperatura | Ciśnienie | Prędkość fali w powietrzu | Praktyczne implikacje |
|---|---|---|---|
| 0°C (273K) | 1 bar | 331 m/s | Wolniejsza reakcja w niskich temperaturach |
| 20°C (293K) | 1 bar | 343 m/s | Standardowe warunki odniesienia |
| 40°C (313K) | 1 bar | 355 m/s | Szybsza reakcja w ciepłym otoczeniu |
| 20°C (293K) | 6 bar | 343 m/s* | Ciśnienie ma minimalny bezpośredni wpływ na prędkość |
*Uwaga: Podczas gdy podstawowa prędkość fali jest niezależna od ciśnienia, na efektywną prędkość w rzeczywistych systemach mogą wpływać wywołane ciśnieniem zmiany elastyczności rur i zachowania gazu.
Praktyczne obliczanie czasu propagacji fal
Dla systemu pneumatycznego z:
- Długość linki (L): 5 metrów
- Temperatura pracy: 20°C (c = 343 m/s)
- Materiał rury: Rura poliuretanowa (zmienia prędkość o około 5%)
Efektywna prędkość fali wynosiłaby:
c_eff = 343 × 0,95 = 326 m/s
A czas propagacji fali wynosiłby:
t = L/c_eff = 5/326 = 0,0153 sekundy (15,3 milisekundy)
Jest to minimalny czas wymagany do zmiany ciśnienia z jednego końca linii na drugi - krytyczny czynnik w aplikacjach o dużej prędkości.
Techniki pomiaru prędkości fali
Do pomiaru rzeczywistej prędkości fali w układach pneumatycznych można wykorzystać kilka metod:
Metoda podwójnego czujnika ciśnienia
- Zainstaluj czujniki ciśnienia w znanych odległościach od siebie
- Tworzenie impulsu ciśnienia (szybkie otwarcie zaworu)
- Pomiar opóźnienia między wzrostem ciśnienia na każdym czujniku
- Oblicz prędkość jako odległość podzieloną przez czas opóźnienia.
Metoda częstotliwości rezonansowej
- Tworzenie oscylacji ciśnienia w zamkniętej rurze
- Zmierz podstawową częstotliwość rezonansową (f)
- Oblicz prędkość przy użyciu c = 2Lf dla rury z zamkniętym końcem
- Weryfikacja za pomocą harmonicznych (nieparzyste wielokrotności podstawowej)
Metoda pomiaru czasu odbicia
- Zainstaluj czujnik ciśnienia w pobliżu zaworu
- Wytworzenie impulsu ciśnienia poprzez szybkie otwarcie zaworu
- Pomiar czasu między impulsem początkowym a impulsem odbitym
- Oblicz prędkość jako 2L podzielone przez czas odbicia
Studium przypadku: Wpływ prędkości fali na reakcję systemu
Dla zrobotyzowanego efektora końcowego z chwytakami pneumatycznymi:
| Parametr | Oryginalny projekt (5 linii) | Zoptymalizowana konstrukcja (1 m linii) | Ulepszenie |
|---|---|---|---|
| Długość linii | 5 metrów | 1 metr | Redukcja 80% |
| Czas propagacji fali | 15,3 ms | 3,1 ms | 12,2 ms szybciej |
| Czas narastania ciśnienia | 28 ms | 9 ms | 19 ms szybciej |
| Stabilność siły chwytu | ±12% | ±3% | Ulepszenie 75% |
| Czas cyklu | 1,2 sekundy | 0,95 sekundy | 21% szybciej |
| Wskaźnik produkcji | 3000 części/godz. | 3780 części/godz. | Wzrost 26% |
To studium przypadku pokazuje, jak zrozumienie i optymalizacja propagacji fal może znacząco wpłynąć na wydajność systemu.
Weryfikacja fali stojącej: W jaki sposób częstotliwości rezonansowe powodują problemy z wydajnością?
Fale stojące powstają, gdy fale ciśnienia odbijają się i interferują ze sobą, tworząc stałe wzorce węzłów i antywęzłów ciśnienia. Te zjawiska rezonansowe mogą powodować poważne problemy z wydajnością systemów pneumatycznych, jeśli nie są odpowiednio rozumiane i zarządzane.
Fale stojące w układach pneumatycznych występują, gdy fale ciśnienia odbijają się na granicach i konstruktywnie interferują, tworząc częstotliwości rezonansowe, w których wahania ciśnienia są wzmacniane. Rezonanse te są zgodne ze wzorem f = nc/2L dla zamkniętych rur, gdzie n jest liczbą harmoniczną, c jest prędkością fali, a L jest długością rury. Weryfikacja eksperymentalna za pomocą czujników ciśnienia, akcelerometrów i pomiarów akustycznych potwierdza te teoretyczne przewidywania i prowadzi do skutecznych strategii łagodzenia.
Podczas ostatniego projektu z producentem urządzeń medycznych w Massachusetts, ich precyzyjny pneumatyczny system pozycjonowania wykazywał tajemnicze wahania siły przy określonych częstotliwościach roboczych. Przeprowadzając testy weryfikacji fali stojącej, zidentyfikowaliśmy, że ich 2,1-metrowa linia zasilająca miała podstawowy rezonans przy 81 Hz - dokładnie odpowiadający częstotliwości cykli siłownika. Rezonans ten wzmacniał wahania ciśnienia przez 320%. Dostosowując długość linii do 1,8 metra, przesunęliśmy częstotliwość rezonansową poza zakres roboczy i całkowicie wyeliminowaliśmy problem, poprawiając dokładność pozycjonowania z ±0,8 mm do ±0,15 mm.
Podstawy fali stojącej
Fale stojące powstają, gdy fale padające i odbite interferują, tworząc stałe wzorce węzłów ciśnienia (minimalna fluktuacja) i antywęzłów (maksymalna fluktuacja).
Częstotliwości rezonansowe linii pneumatycznej zależą od warunków brzegowych:
Dla linii z zamkniętymi końcami (najczęściej w systemach pneumatycznych):
f = nc/2L
Gdzie:
- f = częstotliwość rezonansowa (Hz)
- n = liczba harmoniczna (1, 2, 3 itd.)
- c = Prędkość fali (m/s)
- L = długość linii (m)
Dla linii z jednym otwartym końcem:
f = (2n-1)c/4L
Dla przewodu z otwartymi obydwoma końcami (rzadkość w pneumatyce):
f = nc/2L
Eksperymentalne metody weryfikacji
Kilka technik może weryfikować wzorce fal stojących w układach pneumatycznych:
Układ wielu czujników ciśnienia
- Zainstaluj przetworniki ciśnienia w regularnych odstępach wzdłuż linii pneumatycznej.
- Wzbudzenie systemu za pomocą przemiatania częstotliwości lub impulsu.
- Rejestrowanie wahań ciśnienia w każdej lokalizacji
- Mapowanie amplitudy ciśnienia w zależności od położenia w celu identyfikacji węzłów i przeciwwęzłów
- Porównanie zmierzonych częstotliwości z przewidywaniami teoretycznymi
Korelacja akustyczna
- Wykorzystanie czujników akustycznych (mikrofonów) do wykrywania dźwięku z wahań ciśnienia.
- Korelacja natężenia dźwięku z częstotliwością pracy
- Identyfikacja szczytów natężenia dźwięku odpowiadających częstotliwościom rezonansowym
- Sprawdzić, czy wartości szczytowe występują przy przewidywanych częstotliwościach.
Pomiary akcelerometrem
- Montaż akcelerometrów na przewodach i komponentach pneumatycznych
- Pomiar amplitudy drgań w całym zakresie częstotliwości
- Identyfikacja pików rezonansowych w widmie drgań
- Korelacja z przewidywanymi częstotliwościami fal stojących
Praktyczne obliczanie częstotliwości fali stojącej
Dla typowego systemu pneumatycznego z:
- Długość linki (L): 3 metry
- Prędkość fali (c): 343 m/s
- Konfiguracja z zamkniętymi końcami
Podstawową częstotliwością rezonansową będzie:
f₁ = c/2L = 343/(2×3) = 57,2 Hz
A harmoniczne byłyby następujące:
f₂ = 2f₁ = 114,4 Hz
f₃ = 3f₁ = 171,6 Hz
f₄ = 4f₁ = 228,8 Hz
Częstotliwości te stanowią potencjalne punkty problemowe, w których wahania ciśnienia mogą być wzmacniane.
Wzorce fal stojących i ich efekty
| Harmoniczny | Wzorzec węzła/węzła pośredniego | Efekty systemowe | Krytyczne komponenty, których to dotyczy |
|---|---|---|---|
| Podstawowy (n=1) | Jeden anty-węzeł ciśnienia w środku | Duże wahania ciśnienia w linii środkowej | Komponenty liniowe, złączki |
| Drugi (n=2) | Dwa anty-węzły, węzeł w środku | Zmiany ciśnienia w pobliżu końców | Zawory, siłowniki, regulatory |
| Trzeci (n=3) | Trzy anty-węzły, dwa węzły | Złożony wzór ciśnienia | Wiele komponentów systemu |
| Czwarty (n=4) | Cztery anty-węzły, trzy węzły | Oscylacje o wysokiej częstotliwości | Uszczelki, małe komponenty |
Studium przypadku weryfikacji eksperymentalnej
Dla precyzyjnego pneumatycznego systemu pozycjonowania, którego wydajność jest niestabilna:
| Parametr | Przewidywania teoretyczne | Pomiar eksperymentalny | Korelacja |
|---|---|---|---|
| Częstotliwość podstawowa | 81,2 Hz | 79,8 Hz | 98.3% |
| Druga harmoniczna | 162,4 Hz | 160,5 Hz | 98.8% |
| Trzecia harmoniczna | 243,6 Hz | 240,1 Hz | 98.6% |
| Wzmocnienie ciśnienia | 3:1 przy rezonansie (szacunkowo) | 3,2:1 przy rezonansie (zmierzone) | 93.8% |
| Lokalizacje węzłów | 0, 1,05, 2,1 metra | 0, 1,08, 2,1 metra | 97.2% |
To studium przypadku pokazuje doskonałą zgodność między przewidywaniami teoretycznymi a pomiarami eksperymentalnymi zjawiska fali stojącej.
Praktyczne implikacje fal stojących
Fale stojące stwarzają kilka istotnych problemów w systemach pneumatycznych:
Wzmocnienie ciśnienia
- Wahania mogą być wzmocnione 3-5 razy przy rezonansie
- Może przekraczać wartości znamionowe ciśnienia komponentów
- Tworzy zmiany siły w siłownikachZmęczenie podzespołów
- Cykliczne zmiany ciśnienia o wysokiej częstotliwości przyspieszają zużycie uszczelnienia
- Wibracje powodują poluzowanie złącza i wycieki.
- Skraca żywotność systemu o 30-70% w ciężkich przypadkachNiestabilność kontroli
- Systemy ze sprzężeniem zwrotnym mogą oscylować na częstotliwościach rezonansowych
- Kontrola pozycji i siły staje się nieprzewidywalna
- Może tworzyć samonapędzające się oscylacjeStraty energii
- Fale stojące reprezentują uwięzioną energię
- Może zwiększyć zużycie energii o 10-30%
- Zmniejsza ogólną wydajność systemu
Metody tłumienia impulsów: Jakie techniki skutecznie tłumią destrukcyjne oscylacje ciśnienia?
Kontrolowanie wahań ciśnienia ma zasadnicze znaczenie dla niezawodnego działania systemu pneumatycznego. W celu zmniejszenia lub wyeliminowania problematycznych oscylacji ciśnienia można zastosować różne metody tłumienia.
Tłumienie impulsów ciśnienia w systemach pneumatycznych można osiągnąć za pomocą kilku metod: komór objętościowych, które pochłaniają energię poprzez kompresję gazu, elementów ograniczających, które wytwarzają tłumienie poprzez efekty lepkości, dostrojonych rezonatorów, które anulują określone częstotliwości, oraz aktywnych systemów anulowania, które generują przeciwimpulsy. Skuteczne tłumienie wymaga dopasowania metody do określonej zawartości częstotliwości i amplitudy wahań ciśnienia.
Niedawno współpracowałem z producentem sprzętu do pakowania w Illinois, którego szybki system pneumatyczny doświadczał poważnych wahań ciśnienia, które powodowały niespójne siły uszczelniające. Inżynierowie firmy bezskutecznie próbowali podstawowych zbiorników odbiorczych. Dzięki szczegółowej analizie impulsów ciśnienia zidentyfikowaliśmy, że ich system miał wiele składowych częstotliwości wymagających różnych podejść do tłumienia. Wdrażając hybrydowe rozwiązanie łączące Rezonator Helmholtza5 Dostrojone do ich dominującej oscylacji 112 Hz i serii otworów ograniczających, zmniejszyliśmy wahania ciśnienia o 94% i całkowicie wyeliminowaliśmy niespójności uszczelnienia.
Podstawowe mechanizmy tłumienia
Do tłumienia impulsów ciśnienia można wykorzystać kilka mechanizmów fizycznych:
Tłumienie zależne od objętości
Działa dzięki ściśliwości gazu:
- Zapewnia element zgodności, który pochłania energię nacisku
- Najbardziej skuteczny w przypadku wahań o niskiej częstotliwości
- Prosta implementacja z minimalnym spadkiem ciśnienia
Tłumienie oparte na ograniczeniach
Działa poprzez rozpraszanie lepkości:
- Przekształca energię ciśnienia w ciepło poprzez tarcie
- Skuteczność w szerokim zakresie częstotliwości
- Tworzy stały spadek ciśnienia
Tłumienie oparte na rezonatorze
Działa poprzez dostrojone destrukcyjne zakłócenia:
- Anuluje określone składowe częstotliwości
- Wysoka skuteczność dla ukierunkowanych częstotliwości
- Minimalny wpływ na przepływ w stanie ustalonym
Tłumienie oparte na materiale
Działa dzięki elastyczności i tłumieniu ścian:
- Pochłania energię poprzez deformację ściany
- Zapewnia tłumienie szerokopasmowe
- Możliwość integracji z istniejącymi komponentami
Zasady projektowania komory objętościowej
Komory objętościowe (zbiorniki odbiorcze) są najczęściej stosowanymi urządzeniami tłumiącymi:
Skuteczność komory objętościowej zależy od stosunku objętości komory do objętości linii:
Współczynnik tłumienia = 1 + (Vc/Vl)
Gdzie:
- Vc = objętość komory
- Vl = objętość linii
W przypadku analizy zależnej od częstotliwości współczynnik transmisji wynosi:
TR = 1/√(1 + (ωVc/Zc)²)
Gdzie:
- ω = częstotliwość kątowa (2πf)
- Zc = impedancja charakterystyczna linii
Tłumienie elementów ograniczających
Otwory, porowate materiały i długie wąskie kanały powodują tłumienie poprzez efekty lepkości:
Spadek ciśnienia na ograniczeniu jest następujący:
ΔP = k(ρv²/2)
Gdzie:
- k = Współczynnik strat
- ρ = Gęstość gazu
- v = prędkość
Zapewnione tłumienie wzrasta wraz z:
- Wyższa prędkość przepływu
- Większa długość ograniczenia
- Mniejsza średnica przejścia
- Bardziej kręta ścieżka przepływu
Systemy tłumienia rezonatorów
Dostrojone rezonatory zapewniają ukierunkowane tłumienie częstotliwości:
Rezonator Helmholtza
Komora objętościowa z wąską szyjką, dostrojona do określonej częstotliwości:
f = (c/2π)√(A/VL)
Gdzie:
- f = częstotliwość rezonansowa
- c = prędkość dźwięku
- A = pole przekroju poprzecznego szyi
- V = objętość komory
- L = efektywna długość szyjki
Rezonator ćwierćfalowy
Rura o określonej długości otwarta na jednym końcu:
f = c/4L
Gdzie:
- L = długość rurki
Rezonatory boczne
Wiele dostrojonych gałęzi dla złożonych częstotliwości:
- Każda gałąź jest ukierunkowana na określoną częstotliwość
- Może obsługiwać wiele harmonicznych jednocześnie
- Minimalny wpływ na główną ścieżkę przepływu
Aktywne systemy anulowania
Zaawansowane systemy generujące przeciwimpulsy:
Etap wykrywania
- Wykrywanie przychodzących fal ciśnienia
- Analiza zawartości częstotliwości i amplitudyEtap przetwarzania
- Obliczenie wymaganego sygnału anulowania
- Uwzględnienie dynamiki systemu i opóźnieńEtap uruchamiania
- Generowanie fal przeciwciśnienia
- Precyzyjny czas na destrukcyjną interferencję
Porównanie wydajności tłumienia
| Metoda | Niska częstotliwość (<50 Hz) | Średnia częstotliwość (50-200 Hz) | Wysoka częstotliwość (>200 Hz) | Spadek ciśnienia | Złożoność |
|---|---|---|---|---|---|
| Komora objętościowa | Doskonały (>90%) | Umiarkowany (40-70%) | Słaby (<30%) | Bardzo niski | Niski |
| Otwór ograniczający | Słaby (<30%) | Dobry (60-80%) | Doskonały (>80%) | Wysoki | Niski |
| Rezonator Helmholtza | Słaby rezonans zewnętrzny | Doskonały w rezonansie | Słaby rezonans zewnętrzny | Niski | Średni |
| Rura ćwierćfalowa | Słaby rezonans zewnętrzny | Doskonały w rezonansie | Słaby rezonans zewnętrzny | Niski | Średni |
| Wiele rezonatorów | Umiarkowany (40-60%) | Doskonały (>80%) | Dobry (60-80%) | Niski | Wysoki |
| Aktywne anulowanie | Doskonały (>90%) | Doskonały (>90%) | Dobry (70-85%) | Brak | Bardzo wysoka |
| Systemy hybrydowe | Doskonały (>90%) | Doskonały (>90%) | Doskonały (>90%) | Umiarkowany | Wysoki |
Praktyczna implementacja tłumienia
Dla skutecznego tłumienia impulsów ciśnienia:
Scharakteryzuj wahania
- Pomiar amplitudy i częstotliwości
- Identyfikacja dominujących częstotliwości
- Określenie, czy tłumienia wymagają częstotliwości szerokopasmowe, czy określone częstotliwościWybór odpowiednich metod
- Dla niskich częstotliwości: Komory objętościowe
- Dla określonych częstotliwości: Dostrojone rezonatory
- Dla tłumienia szerokopasmowego: Ograniczenia lub podejścia hybrydowe
- Do zastosowań krytycznych: Aktywne anulowanieOptymalizacja rozmieszczenia
- W pobliżu źródeł, aby zapobiec rozprzestrzenianiu się
- W pobliżu wrażliwych komponentów w celu ich ochrony
- W strategicznych miejscach, aby przełamać wzorce fal stojącychWeryfikacja wydajności
- Pomiar przed/po tłumieniu
- Potwierdzenie w różnych warunkach pracy
- Zapewnienie braku niezamierzonych konsekwencji
Studium przypadku: Wielometodowe tłumienie w szybkich opakowaniach
Do szybkiego pneumatycznego systemu uszczelniającego, w którym występują wahania ciśnienia:
| Parametr | Przed tłumieniem | Po komorze objętościowej | Po rozwiązaniu hybrydowym | Ulepszenie |
|---|---|---|---|---|
| Niska częstotliwość (<50 Hz) | ±0,8 bar | ±0,12 bar | ±0,05 bar | Redukcja 94% |
| Średnia częstotliwość (112 Hz) | ±1,2 bar | ±0,85 bar | ±0,07 bar | Redukcja 94% |
| Wysoka częstotliwość (>200 Hz) | ±0,4 bar | ±0,36 bar | ±0,04 bar | Redukcja 90% |
| Zmienność siły uszczelnienia | ±28% | ±22% | ±2,5% | Ulepszenie 91% |
| Współczynnik odrzucenia produktu | 4.2% | 3.1% | 0.3% | Redukcja 93% |
| Wydajność systemu | Linia bazowa | +4% | +12% | Ulepszenie 12% |
To studium przypadku pokazuje, jak ukierunkowane, wielometodowe podejście do tłumienia może znacznie poprawić wydajność systemu.
Zaawansowane techniki tłumienia
Dla szczególnie wymagających aplikacji:
Rozproszone tłumienie
Korzystanie z wielu mniejszych urządzeń zamiast jednego dużego:
- Umieszcza tłumienie bliżej źródeł i wrażliwych komponentów
- Skuteczniej rozbija fale stojące
- Zapewnia redundancję i bardziej spójną wydajność
Tłumienie z selekcją częstotliwości
Ukierunkowanie na określone problematyczne częstotliwości:
- Wykorzystuje wiele rezonatorów dostrojonych do różnych częstotliwości
- Zachowuje pożądaną reakcję systemu, jednocześnie eliminując problemy
- Minimalizuje wpływ na ogólną wydajność systemu
Systemy adaptacyjne
Regulacja tłumienia w zależności od warunków pracy:
- Wykorzystuje czujniki do monitorowania wahań ciśnienia
- Automatycznie dostosowuje parametry tłumienia
- Optymalizuje wydajność w różnych warunkach
Wnioski
Zrozumienie teorii wahań ciśnienia - prędkości rozchodzenia się fali, weryfikacji fali stojącej i metod tłumienia impulsów - stanowi podstawę niezawodnego i wydajnego projektowania układów pneumatycznych. Stosując te zasady, można wyeliminować tajemnicze problemy z wydajnością, wydłużyć żywotność komponentów i poprawić wydajność systemu, zapewniając jednocześnie spójne działanie we wszystkich warunkach pracy.
Najczęściej zadawane pytania dotyczące wahań ciśnienia w układach pneumatycznych
Jak wahania ciśnienia wpływają na żywotność komponentów pneumatycznych?
Wahania ciśnienia znacznie skracają żywotność komponentów poprzez kilka mechanizmów: powodują przyspieszone zużycie uszczelnienia poprzez tworzenie mikroruchów na powierzchniach uszczelniających; powodują zmęczenie materiału w membranach i elementach elastycznych poprzez powtarzające się cykle naprężeń; sprzyjają poluzowaniu połączeń gwintowych poprzez wibracje; i tworzą lokalne koncentracje naprężeń na przejściach geometrycznych. Systemy z poważnymi niekontrolowanymi wahaniami ciśnienia zazwyczaj doświadczają 40-70% krótszej żywotności komponentów w porównaniu z prawidłowo wytłumionymi systemami, przy czym uszczelki i membrany są szczególnie wrażliwe.
Jaki jest związek między długością przewodu a czasem reakcji na ciśnienie w układach pneumatycznych?
Długość linii bezpośrednio wpływa na czas reakcji na ciśnienie zgodnie z prostą zależnością: czas reakcji wzrasta liniowo wraz z długością linii w tempie określonym przez prędkość propagacji fali. Dla powietrza w standardowych warunkach (prędkość fali ≈ 343 m/s), każdy metr linii dodaje około 2,9 milisekundy opóźnienia transmisji. Jednak rzeczywisty czas narastania ciśnienia jest zwykle 2-5 razy dłuższy niż początkowy czas transmisji fali ze względu na potrzebę wielokrotnych odbić w celu wyrównania ciśnienia. Oznacza to, że 5-metrowa linia może mieć czas transmisji fali 14,5 ms, ale czas narastania ciśnienia 30-70 ms.
Jak mogę zidentyfikować, czy mój system pneumatyczny doświadcza rezonansowych wahań ciśnienia?
Wahania ciśnienia rezonansowego zwykle objawiają się kilkoma obserwowalnymi objawami: komponenty wibrują przy określonych częstotliwościach roboczych, ale nie przy innych; wydajność systemu zmienia się niespójnie przy niewielkich zmianach warunków pracy; słychać "śpiew" lub "gwizdanie" z przewodów pneumatycznych; manometry pokazują oscylujące odczyty; a wydajność siłownika (prędkość, siła) zmienia się cyklicznie. Aby potwierdzić rezonans, należy zmierzyć ciśnienie w różnych punktach systemu za pomocą szybko reagujących przetworników (czas reakcji <1 ms) i poszukać wzorów fali stojącej, w których amplituda ciśnienia zmienia się wraz z położeniem wzdłuż linii.
Czy wahania ciśnienia wpływają na efektywność energetyczną systemów pneumatycznych?
Wahania ciśnienia znacząco wpływają na efektywność energetyczną, zazwyczaj zmniejszając ją o 10-25% poprzez kilka mechanizmów: zwiększają wskaźniki wycieków poprzez tworzenie wyższych ciśnień szczytowych; marnują energię w cyklicznym sprężaniu i rozprężaniu; powodują zwiększone tarcie w komponentach z powodu wibracji; i często prowadzą operatorów do zwiększenia ciśnienia zasilania w celu skompensowania problemów z wydajnością. Dodatkowo, turbulencje i separacja przepływu tworzone przez wahania ciśnienia przekształcają użyteczną energię ciśnienia w ciepło odpadowe. Odpowiednie tłumienie wahań ciśnienia może poprawić wydajność systemu o 5-15% bez żadnych innych zmian.
Jak zmiany temperatury wpływają na zachowanie fali ciśnienia w układach pneumatycznych?
Temperatura znacząco wpływa na zachowanie fal ciśnieniowych poprzez kilka mechanizmów: bezpośrednio wpływa na prędkość propagacji fal (około +0,6 m/s na wzrost temperatury); zmienia gęstość i lepkość gazu, zmieniając charakterystykę tłumienia; modyfikuje właściwości sprężyste przewodów pneumatycznych, wpływając na odbicie i przenoszenie fal; oraz przesuwa częstotliwości rezonansowe (około +0,17% na °C). Ta wrażliwość na temperaturę oznacza, że system, który działa idealnie w temperaturze 20°C, może doświadczać problematycznych rezonansów podczas pracy w temperaturze 40°C lub że urządzenia tłumiące dostrojone do warunków zimowych mogą być nieskuteczne latem.
-
Zawiera szczegółowe wyjaśnienie fizyki stojącej za prędkością dźwięku, sposobu jej obliczania i czynników, które na nią wpływają. ↩
-
Oferuje fundamentalne zrozumienie zjawisk fal stojących, w tym tego, jak powstają one w wyniku interferencji i ich kluczowych cech, takich jak węzły i anty-węzły. ↩
-
Dostarcza dowodów i badań branżowych, które weryfikują typowy zakres strat energii spowodowanych nieefektywnością, taką jak wahania ciśnienia w układach pneumatycznych. ↩
-
Wyjaśnia elementy i funkcje jednostki przygotowania powietrza (FRL), która jest niezbędna do utrzymania jakości powietrza w układach pneumatycznych. ↩
-
Oferuje dogłębne wyjaśnienie zasad działania rezonatora Helmholtza, krytycznego urządzenia do tłumienia częstotliwości w systemach akustycznych i płynowych. ↩



