Como é que as flutuações de pressão afectam o desempenho do seu sistema pneumático?

Já se apercebeu de vibrações misteriosas nas suas linhas pneumáticas? Ou variações inexplicáveis de força nos seus cilindros, apesar da pressão de alimentação estável? Estes fenómenos não são aleatórios - são o resultado de ondas de pressão que se propagam através do seu sistema, criando efeitos que podem ir desde pequenas ineficiências a falhas catastróficas.

As flutuações de pressão nos sistemas pneumáticos são fenómenos ondulatórios que se propagam a velocidades próximas da velocidade do som¹, criando efeitos dinâmicos, incluindo ressonância, ondas estacionárias²e amplificação da pressão. Compreender estas flutuações é crucial porque podem causar fadiga dos componentes, instabilidade do controlo e perdas de energia de 10-25% em sistemas industriais típicos³.

No mês passado, prestei consultoria a uma fábrica de montagem automóvel no Tennessee, onde um sistema de fixação pneumático crítico estava a sofrer variações intermitentes de força, apesar da pressão de alimentação estável. A sua equipa de manutenção tinha substituído válvulas, reguladores e até mesmo todo o unidade de preparação do ar⁴ sem sucesso. Ao analisar a dinâmica da onda de pressão - particularmente os padrões de onda estacionária nas suas linhas de abastecimento - identificámos que estavam a funcionar a uma frequência que criava uma interferência destrutiva no cilindro. Um simples ajuste no comprimento da linha eliminou o problema e poupou-lhes semanas de atrasos na produção. Deixe-me mostrar-lhe como a compreensão da teoria da flutuação de pressão pode transformar a fiabilidade do seu sistema pneumático.

Índice

• Velocidade de propagação da onda: Com que rapidez as perturbações de pressão viajam no seu sistema?
• Verificação de onda estacionária: Como é que as frequências ressonantes criam problemas de desempenho?
• Métodos de Atenuação de Impulsos: Que técnicas atenuam eficazmente as oscilações de pressão destrutivas?
• Conclusão
• Perguntas frequentes sobre flutuações de pressão em sistemas pneumáticos

Velocidade de propagação da onda: Com que rapidez as perturbações de pressão viajam no seu sistema?

Compreender a rapidez com que as perturbações de pressão se propagam através dos sistemas pneumáticos é fundamental para prever e controlar os seus efeitos. A velocidade de propagação determina o tempo de resposta do sistema, as frequências de ressonância e o potencial de interferência destrutiva.

As ondas de pressão em sistemas pneumáticos viajam à velocidade do som no meio gasoso, que pode ser calculada através da fórmula c = √(γRT), em que γ é o rácio de calor específico, R é a constante específica do gás e T é a temperatura absoluta. Para o ar a 20°C, isto equivale a aproximadamente 343 m/s, embora esta velocidade seja modificada por factores que incluem a elasticidade do tubo, a compressibilidade do gás e as condições de fluxo.

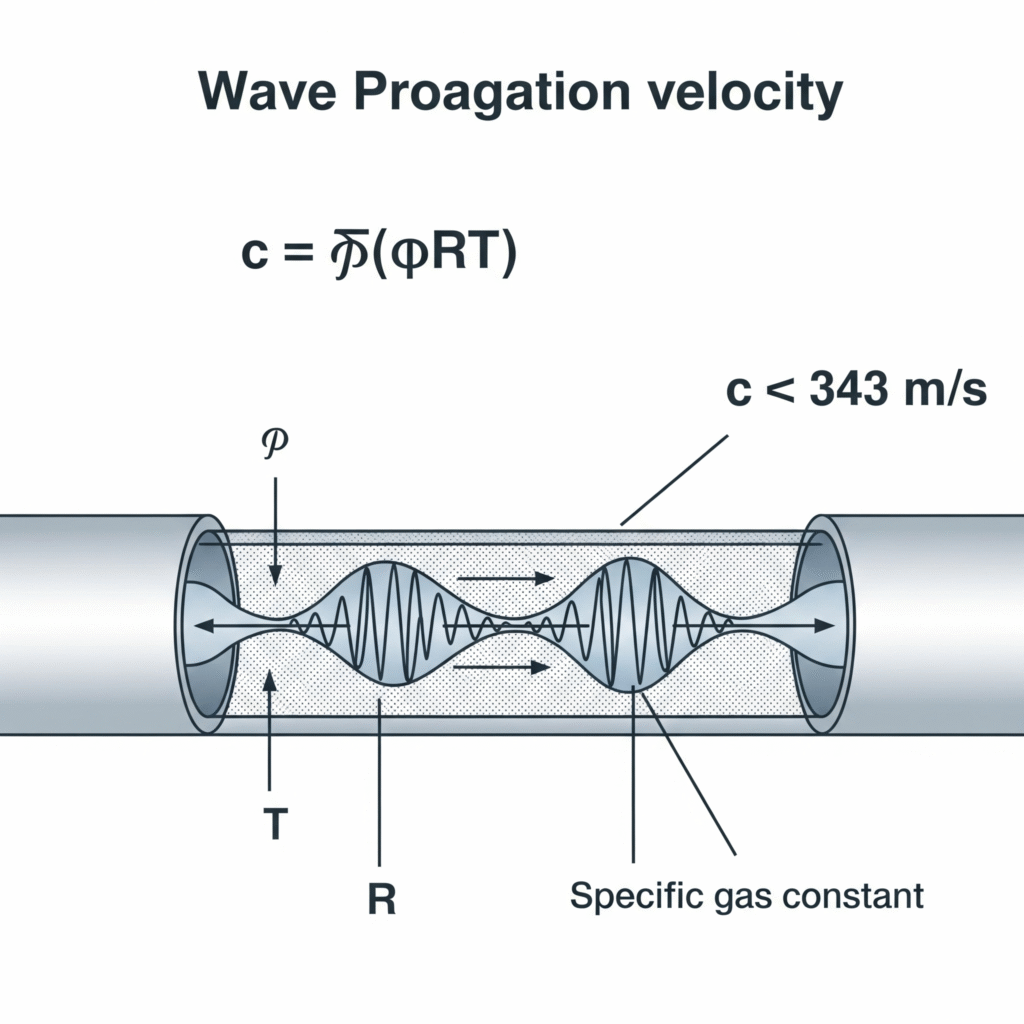
Recentemente, ajudei a resolver problemas numa máquina de montagem de precisão na Suíça, onde as pinças pneumáticas apresentavam um atraso de 12 ms entre a ativação e a aplicação de força - uma eternidade num ambiente de produção de alta velocidade. Os seus engenheiros tinham assumido uma transmissão instantânea da pressão. Ao medir a velocidade real de propagação da onda no seu sistema (328 m/s) e tendo em conta o comprimento da linha de 4 metros, calculámos um tempo de transmissão teórico de 12,2 ms - quase exatamente igual ao atraso observado. A deslocação das válvulas para mais perto dos actuadores reduziu este atraso para 3ms e aumentou a taxa de produção em 14%.

Equações fundamentais da velocidade da onda

A equação básica para a velocidade de propagação de ondas de pressão num gás é

c = √(γRT)

Onde:

• c = Velocidade de propagação da onda (m/s)
• γ = Rácio de calor específico (1,4 para o ar)
• R = Constante específica dos gases (287 J/kg-K para o ar)
• T = Temperatura absoluta (K)

Para o ar a 20°C (293K), isto dá:
c = √(1,4 × 287 × 293) = 343 m/s

Velocidade de onda modificada em linhas pneumáticas

Nos sistemas pneumáticos reais, a velocidade efectiva da onda é modificada pela elasticidade do tubo e por outros factores, de acordo com a fórmula:

c_eff = c / √(1 + (Dψ/Eh))

Onde:

• c_eff = Velocidade efectiva da onda (m/s)
• D = Diâmetro do tubo (m)
• ψ = Fator de compressibilidade do gás
• E = Módulo de elasticidade do material do tubo (Pa)
• h = Espessura da parede do tubo (m)

Efeitos da temperatura e da pressão na velocidade da onda

A velocidade da onda varia consoante as condições de funcionamento:

Temperatura	Pressão	Velocidade da onda no ar	Implicações práticas
0°C (273K)	1 barra	331 m/s	Resposta mais lenta em ambientes frios
20°C (293K)	1 barra	343 m/s	Condição de referência padrão
40°C (313K)	1 barra	355 m/s	Resposta mais rápida em ambientes quentes
20°C (293K)	6 barras	343 m/s*	A pressão tem um efeito direto mínimo na velocidade

*Nota: Embora a velocidade básica da onda seja independente da pressão, a velocidade efectiva em sistemas reais pode ser afetada por alterações induzidas pela pressão na elasticidade da tubagem e no comportamento do gás.

Cálculo prático do tempo de propagação da onda

Para um sistema pneumático com:

• Comprimento da linha (L): 5 metros
• Temperatura de funcionamento: 20°C (c = 343 m/s)
• Material da tubagem: Tubagem de poliuretano (altera a velocidade em cerca de 5%)

A velocidade efectiva da onda seria:
c_eff = 343 × 0,95 = 326 m/s

E o tempo de propagação da onda seria:
t = L/c_eff = 5/326 = 0,0153 segundos (15,3 milissegundos)

Isto representa o tempo mínimo necessário para que uma alteração de pressão se desloque de uma extremidade da linha para a outra - um fator crítico em aplicações de alta velocidade.

Técnicas de medição da velocidade da onda

Podem ser utilizados vários métodos para medir a velocidade real da onda em sistemas pneumáticos:

Método do sensor de pressão duplo

1. Instalar sensores de pressão a distâncias conhecidas
2. Criar um impulso de pressão (abertura rápida da válvula)
3. Medir o tempo de atraso entre o aumento da pressão em cada sensor
4. Calcular a velocidade como a distância dividida pelo tempo de atraso

Método da frequência ressonante

1. Criar oscilações de pressão num tubo fechado
2. Medir a frequência fundamental de ressonância (f)
3. Calcular a velocidade usando c = 2Lf para um tubo de extremidade fechada
4. Verificar com harmónicos (múltiplos ímpares da fundamental)

Método do tempo de reflexão

1. Instalar um sensor de pressão perto de uma válvula
2. Criar um impulso de pressão abrindo rapidamente a válvula
3. Medir o tempo entre o impulso inicial e o impulso refletido
4. Calcular a velocidade como 2L dividido pelo tempo de reflexão

Estudo de caso: Impacto da velocidade da onda na resposta do sistema

Para um end-effector robótico com pinças pneumáticas:

Parâmetro	Desenho original (5m linhas)	Design optimizado (1m linhas)	Melhoria
Comprimento da linha	5 metros	1 metro	Redução 80%
Tempo de propagação da onda	15,3 ms	3,1 ms	12,2 ms mais rápido
Tempo de acumulação de pressão	28 ms	9 ms	19 ms mais rápido
Estabilidade da força de preensão	Variação de ±12%	Variação ±3%	Melhoria do 75%
Tempo de ciclo	1,2 segundos	0,95 segundos	21% mais rápido
Taxa de produção	3000 peças/hora	3780 peças/hora	Aumento de 26%

Este estudo de caso demonstra como compreender e otimizar a propagação de ondas pode ter um impacto significativo no desempenho do sistema.

Verificação de onda estacionária: Como é que as frequências ressonantes criam problemas de desempenho?

As ondas estacionárias ocorrem quando as ondas de pressão se reflectem e interferem entre si, criando padrões fixos de nós e antinós de pressão. Estes fenómenos de ressonância podem causar graves problemas de desempenho em sistemas pneumáticos se não forem devidamente compreendidos e geridos.

As ondas estacionárias em sistemas pneumáticos ocorrem quando as ondas de pressão reflectem nos limites e interferem construtivamente, criando frequências ressonantes onde as flutuações de pressão são amplificadas. Estas ressonâncias seguem a fórmula f = nc/2L para tubos fechados, em que n é o número harmónico, c é a velocidade da onda e L é o comprimento do tubo. A verificação experimental através de sensores de pressão, acelerómetros e medições acústicas confirma estas previsões teóricas e orienta estratégias de atenuação eficazes.

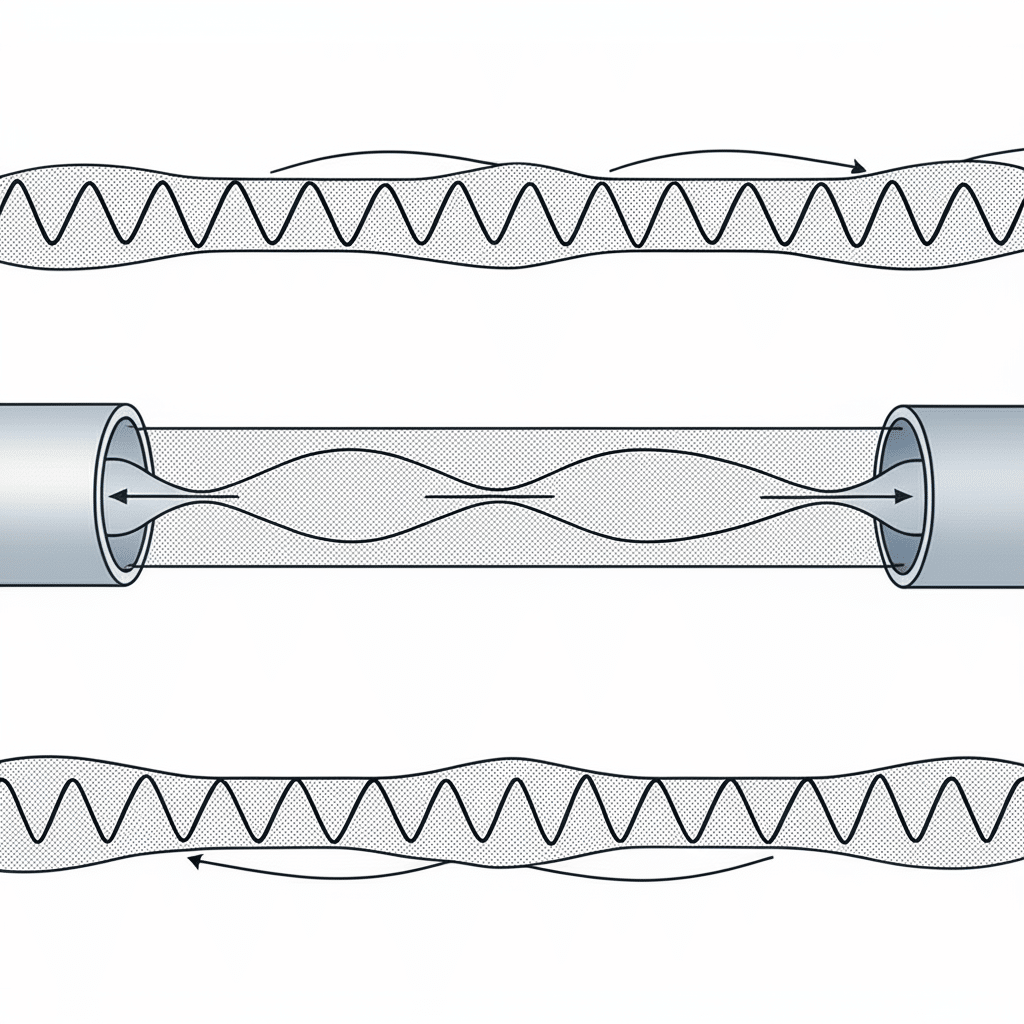
Durante um projeto recente com um fabricante de dispositivos médicos em Massachusetts, o seu sistema de posicionamento pneumático de precisão estava a apresentar flutuações de força misteriosas em frequências de funcionamento específicas. Ao realizar testes de verificação de ondas estacionárias, identificámos que a sua linha de alimentação de 2,1 metros tinha uma ressonância fundamental a 81 Hz - correspondendo precisamente à frequência de ciclo do seu atuador. Esta ressonância estava a amplificar as flutuações de pressão em 320%. Ao ajustar o comprimento da linha para 1,8 metros, afastámos a frequência de ressonância da sua gama de funcionamento e eliminámos completamente o problema, melhorando a precisão do posicionamento de ±0,8 mm para ±0,15 mm.

Fundamentos da onda estacionária

As ondas estacionárias formam-se quando as ondas incidentes e reflectidas interferem, criando padrões fixos de nós de pressão (flutuação mínima) e antinós (flutuação máxima).

As frequências de ressonância de uma linha pneumática dependem das condições de fronteira:

Para uma linha com extremidades fechadas (mais comum em sistemas pneumáticos):

f = nc/2L

Onde:

• f = Frequência ressonante (Hz)
• n = Número harmónico (1, 2, 3, etc.)
• c = Velocidade da onda (m/s)
• L = Comprimento da linha (m)

Para uma linha com uma extremidade aberta:

f = (2n-1)c/4L

Para uma linha com ambas as extremidades abertas (raro em pneumática):

f = nc/2L

Métodos de verificação experimental

Várias técnicas podem verificar padrões de ondas estacionárias em sistemas pneumáticos:

Conjunto de vários sensores de pressão

1. Instalar transdutores de pressão a intervalos regulares ao longo da linha pneumática
2. Excitar o sistema com uma varredura de frequência ou impulso
3. Registar as flutuações de pressão em cada local
4. Mapear a amplitude da pressão vs. posição para identificar nós e antinós
5. Comparar as frequências medidas com as previsões teóricas

Correlação acústica

1. Utilizar sensores acústicos (microfones) para detetar o som das flutuações de pressão
2. Correlacionar a intensidade do som com a frequência de funcionamento
3. Identificar os picos de intensidade sonora correspondentes às frequências de ressonância
4. Verificar se os picos ocorrem nas frequências previstas

Medições do acelerómetro

1. Montar acelerómetros em linhas e componentes pneumáticos
2. Medir a amplitude da vibração em toda a gama de frequências
3. Identificar picos ressonantes no espetro de vibração
4. Correlacionar com as frequências de ondas estacionárias previstas

Cálculo prático da frequência da onda estacionária

Para um sistema pneumático típico com:

• Comprimento da linha (L): 3 metros
• Velocidade da onda (c): 343 m/s
• Configuração de extremidades fechadas

A frequência fundamental de ressonância seria:
f₁ = c/2L = 343/(2×3) = 57,2 Hz

E os harmónicos seriam:
f₂ = 2f₁ = 114,4 Hz
f₃ = 3f₁ = 171,6 Hz
f₄ = 4f₁ = 228,8 Hz

Estas frequências representam potenciais pontos problemáticos onde as flutuações de pressão podem ser amplificadas.

Padrões de ondas estacionárias e seus efeitos

Harmónico	Padrão de Nó/Antinodo	Efeitos do sistema	Componentes críticos afectados
Fundamental (n=1)	Um antinó de pressão no centro	Grandes variações de pressão a meio da linha	Componentes em linha, acessórios
Segundo (n=2)	Dois antinós, nó no centro	Variações de pressão perto das extremidades	Válvulas, actuadores, reguladores
Terceiro (n=3)	Três antinós, dois nós	Padrão de pressão complexo	Componentes múltiplos do sistema
Quarto (n=4)	Quatro antinós, três nós	Oscilações de alta frequência	Vedantes, pequenos componentes

Estudo de caso de verificação experimental

Para um sistema de posicionamento pneumático de precisão com um desempenho inconsistente:

Parâmetro	Previsão teórica	Medição experimental	Correlação
Frequência fundamental	81,2 Hz	79,8 Hz	98.3%
Segundo harmónico	162,4 Hz	160,5 Hz	98.8%
Terceiro harmónico	243,6 Hz	240,1 Hz	98.6%
Amplificação da pressão	3:1 na ressonância (estimado)	3,2:1 na ressonância (medido)	93.8%
Localização dos nós	0, 1,05, 2,1 metros	0, 1,08, 2,1 metros	97.2%

Este estudo de caso demonstra a excelente concordância entre as previsões teóricas e as medições experimentais de fenómenos de ondas estacionárias.

Implicações práticas das ondas estacionárias

As ondas estacionárias criam vários problemas significativos nos sistemas pneumáticos:

1. Amplificação da pressão
      - As flutuações podem ser amplificadas 3-5 vezes na ressonância
      - Pode exceder as classificações de pressão dos componentes
      - Cria variações de força nos actuadores

   
   

2. Fadiga de componentes
      - O ciclo de pressão de alta frequência acelera o desgaste dos vedantes
      - A vibração provoca o afrouxamento dos encaixes e fugas
      - Reduz a vida útil do sistema em 30-70% em casos graves

   
   

3. Instabilidade de controlo
      - Os sistemas de realimentação podem oscilar a frequências ressonantes
      - O controlo da posição e da força torna-se imprevisível
      - Pode criar oscilações que se auto-reforçam

   
   

4. Perdas de energia
      - As ondas estacionárias representam energia aprisionada
      - Pode aumentar o consumo de energia em 10-30%
      - Reduz a eficiência global do sistema

   
   

Métodos de Atenuação de Impulsos: Que técnicas atenuam eficazmente as oscilações de pressão destrutivas?

O controlo das flutuações de pressão é essencial para um funcionamento fiável do sistema pneumático. Podem ser utilizados vários métodos de atenuação para reduzir ou eliminar as problemáticas oscilações de pressão.

A atenuação de impulsos de pressão em sistemas pneumáticos pode ser conseguida através de vários métodos: câmaras de volume que absorvem energia através da compressão de gás, elementos restritivos que criam amortecimento através de efeitos viscosos, ressonadores sintonizados que cancelam frequências específicas e sistemas de cancelamento ativo que geram contra-pulsos. A atenuação efectiva requer a adequação do método ao conteúdo específico da frequência e à amplitude das flutuações de pressão.

Recentemente, trabalhei com um fabricante de equipamento de embalagem no Illinois cujo sistema pneumático de alta velocidade estava a sofrer graves flutuações de pressão que causavam forças de vedação inconsistentes. Os seus engenheiros tinham tentado tanques receptores básicos sem sucesso. Através de uma análise detalhada dos impulsos de pressão, identificámos que o seu sistema tinha vários componentes de frequência que exigiam diferentes abordagens de atenuação. Ao implementar uma solução híbrida que combina um Ressonador Helmholtz⁵ sintonizados com a sua oscilação dominante de 112 Hz e uma série de orifícios de restrição, reduzimos as flutuações de pressão em 94% e eliminámos completamente as inconsistências de vedação.

Mecanismos fundamentais de atenuação

Podem ser utilizados vários mecanismos físicos para atenuar os impulsos de pressão:

Atenuação baseada no volume

Funciona através da compressibilidade do gás:

• Fornece um elemento de conformidade que absorve a energia da pressão
• Mais eficaz para flutuações de baixa frequência
• Implementação simples com queda de pressão mínima

Atenuação baseada em restrições

Funciona através de dissipação viscosa:

• Converte a energia da pressão em calor através da fricção
• Eficaz numa vasta gama de frequências
• Cria uma queda de pressão permanente

Atenuação baseada em ressonador

Funciona através de interferência destrutiva sintonizada:

• Cancela componentes de frequência específicos
• Altamente eficaz para frequências específicas
• Impacto mínimo no fluxo em estado estacionário

Atenuação baseada em materiais

Funciona através da flexibilidade e do amortecimento das paredes:

• Absorve energia através da deformação da parede
• Proporciona atenuação de banda larga
• Pode ser integrado em componentes existentes

Princípios de conceção da câmara de volume

As câmaras de volume (tanques receptores) são os dispositivos de atenuação mais comuns:

A eficácia de uma câmara volumétrica depende da relação entre o volume da câmara e o volume da linha:

Razão de atenuação = 1 + (Vc/Vl)

Onde:

• Vc = Volume da câmara
• Vl = Volume da linha

Para uma análise dependente da frequência, a relação de transmissão é:

TR = 1/√(1 + (ωVc/Zc)²)

Onde:

• ω = Frequência angular (2πf)
• Zc = Impedância caraterística da linha

Atenuação de elementos restritivos

Orifícios, materiais porosos e passagens longas e estreitas criam atenuação através de efeitos viscosos:

A queda de pressão através de uma restrição é a seguinte:

ΔP = k(ρv²/2)

Onde:

• k = Coeficiente de perdas
• ρ = Densidade do gás
• v = Velocidade

A atenuação fornecida aumenta com:

• Maior velocidade de fluxo
• Maior comprimento da restrição
• Diâmetro de passagem mais pequeno
• Trajeto do fluxo mais tortuoso

Sistemas de atenuação de ressonadores

Os ressoadores sintonizados proporcionam uma atenuação de frequência direcionada:

Ressonador Helmholtz

Uma câmara volumétrica com um gargalo estreito, sintonizada numa frequência específica:

f = (c/2π)√(A/VL)

Onde:

• f = Frequência ressonante
• c = Velocidade do som
• A = Área da secção transversal do pescoço
• V = Volume da câmara
• L = Comprimento efetivo do pescoço

Ressonador de quarto de onda

Um tubo de comprimento específico aberto numa extremidade:

f = c/4L

Onde:

• L = Comprimento do tubo

Ressonadores de ramo lateral

Múltiplos ramos sintonizados para conteúdos de frequência complexos:

• Cada ramo visa uma frequência específica
• Pode tratar vários harmónicos em simultâneo
• Impacto mínimo no percurso do fluxo principal

Sistemas de cancelamento ativo

Sistemas avançados que geram contra-pulsos:

1. Fase de deteção
      - Detetar ondas de pressão de entrada
      - Analisar o conteúdo de frequência e a amplitude

   
   

2. Fase de processamento
      - Calcular o sinal de cancelamento necessário
      - Ter em conta a dinâmica e os atrasos do sistema

   
   

3. Fase de acionamento
      - Gerar ondas de contra-pressão
      - Tempo exato para a interferência destrutiva

   
   

Comparação do desempenho da atenuação

Método	Baixa frequência (<50 Hz)	Frequência média (50-200 Hz)	Alta frequência (>200 Hz)	Queda de pressão	Complexidade
Câmara de volume	Excelente (>90%)	Moderado (40-70%)	Fraco (<30%)	Muito baixo	Baixa
Orifício restritivo	Fraco (<30%)	Bom (60-80%)	Excelente (>80%)	Elevado	Baixa
Ressonador Helmholtz	Fraca ressonância exterior	Excelente em ressonância	Fraca ressonância exterior	Baixa	Médio
Tubo de quarto de onda	Fraca ressonância exterior	Excelente em ressonância	Fraca ressonância exterior	Baixa	Médio
Ressonadores múltiplos	Moderado (40-60%)	Excelente (>80%)	Bom (60-80%)	Baixa	Elevado
Cancelamento ativo	Excelente (>90%)	Excelente (>90%)	Bom (70-85%)	Nenhum	Muito elevado
Sistemas híbridos	Excelente (>90%)	Excelente (>90%)	Excelente (>90%)	Moderado	Elevado

Implementação prática da atenuação

Para uma atenuação eficaz dos impulsos de pressão:

1. Caracterizar as flutuações
      - Medir a amplitude e o conteúdo de frequência
      - Identificar as frequências dominantes
      - Determinar se a banda larga ou frequências específicas necessitam de atenuação

   
   

2. Selecionar métodos adequados
      - Para baixas frequências: Câmaras de volume
      - Para frequências específicas: Ressonadores sintonizados
      - Para atenuação de banda larga: Restrições ou abordagens híbridas
      - Para aplicações críticas: Cancelamento ativo

   
   

3. Otimizar a colocação
      - Perto de fontes para evitar a propagação
      - Perto de componentes sensíveis para os proteger
      - Em locais estratégicos para quebrar os padrões de ondas estacionárias

   
   

4. Verificar o desempenho
      - Medir antes/depois da atenuação
      - Confirmar as condições de funcionamento
      - Garantir que não haja consequências indesejadas

   
   

Estudo de caso: Atenuação por vários métodos em embalagens de alta velocidade

Para um sistema de vedação pneumático de alta velocidade com flutuações de pressão:

Parâmetro	Antes da atenuação	Depois da câmara de volume	Depois da solução híbrida	Melhoria
Baixa frequência (<50 Hz)	±0,8 bar	±0,12 bar	±0,05 bar	Redução 94%
Frequência média (112 Hz)	±1,2 bar	±0,85 bar	±0,07 bar	Redução 94%
Alta frequência (>200 Hz)	±0,4 bar	±0,36 bar	±0,04 bar	Redução 90%
Variação da força de vedação	±28%	±22%	±2,5%	Melhoria do 91%
Taxa de rejeição de produtos	4.2%	3.1%	0.3%	Redução 93%
Eficiência do sistema	Linha de base	+4%	+12%	Melhoria 12%

Este estudo de caso demonstra como uma abordagem de atenuação orientada e com vários métodos pode melhorar drasticamente o desempenho do sistema.

Técnicas avançadas de atenuação

Para aplicações particularmente exigentes:

Atenuação distribuída

Utilizar vários dispositivos mais pequenos em vez de um grande:

• Coloca a atenuação mais perto das fontes e dos componentes sensíveis
• Quebra os padrões de ondas estacionárias de forma mais eficaz
• Proporciona redundância e um desempenho mais consistente

Amortecimento seletivo de frequência

Direcionar frequências problemáticas específicas:

• Utiliza vários ressoadores sintonizados em diferentes frequências
• Preserva a resposta desejada do sistema, eliminando os problemas
• Minimiza o impacto no desempenho geral do sistema

Sistemas adaptativos

Ajustar a atenuação com base nas condições de funcionamento:

• Utiliza sensores para monitorizar as flutuações de pressão
• Ajusta automaticamente os parâmetros de atenuação
• Optimiza o desempenho em condições variáveis

Conclusão

A compreensão da teoria da flutuação da pressão - velocidade de propagação da onda, verificação da onda estacionária e métodos de atenuação de impulsos - fornece a base para uma conceção fiável e eficiente do sistema pneumático. Ao aplicar estes princípios, pode eliminar problemas de desempenho misteriosos, prolongar a vida útil dos componentes e melhorar a eficiência do sistema, assegurando simultaneamente um funcionamento consistente em todas as condições de funcionamento.

Perguntas frequentes sobre flutuações de pressão em sistemas pneumáticos

1. Fornece uma explicação detalhada da física subjacente à velocidade do som, como é calculada e os factores que a influenciam. ↩

2. Oferece uma compreensão fundamental dos fenómenos de ondas estacionárias, incluindo a forma como se formam a partir da interferência e as suas principais caraterísticas, como nós e antinós. ↩

3. Fornece provas e estudos industriais que verificam a gama típica de perdas de energia causadas por ineficiências como as flutuações de pressão em sistemas pneumáticos. ↩

4. Explica os componentes e a função de uma unidade de preparação de ar (FRL), essencial para manter a qualidade do ar em sistemas pneumáticos. ↩

5. Oferece uma explicação aprofundada dos princípios subjacentes a um ressoador de Helmholtz, um dispositivo essencial para a atenuação de frequências específicas em sistemas acústicos e de fluidos. ↩