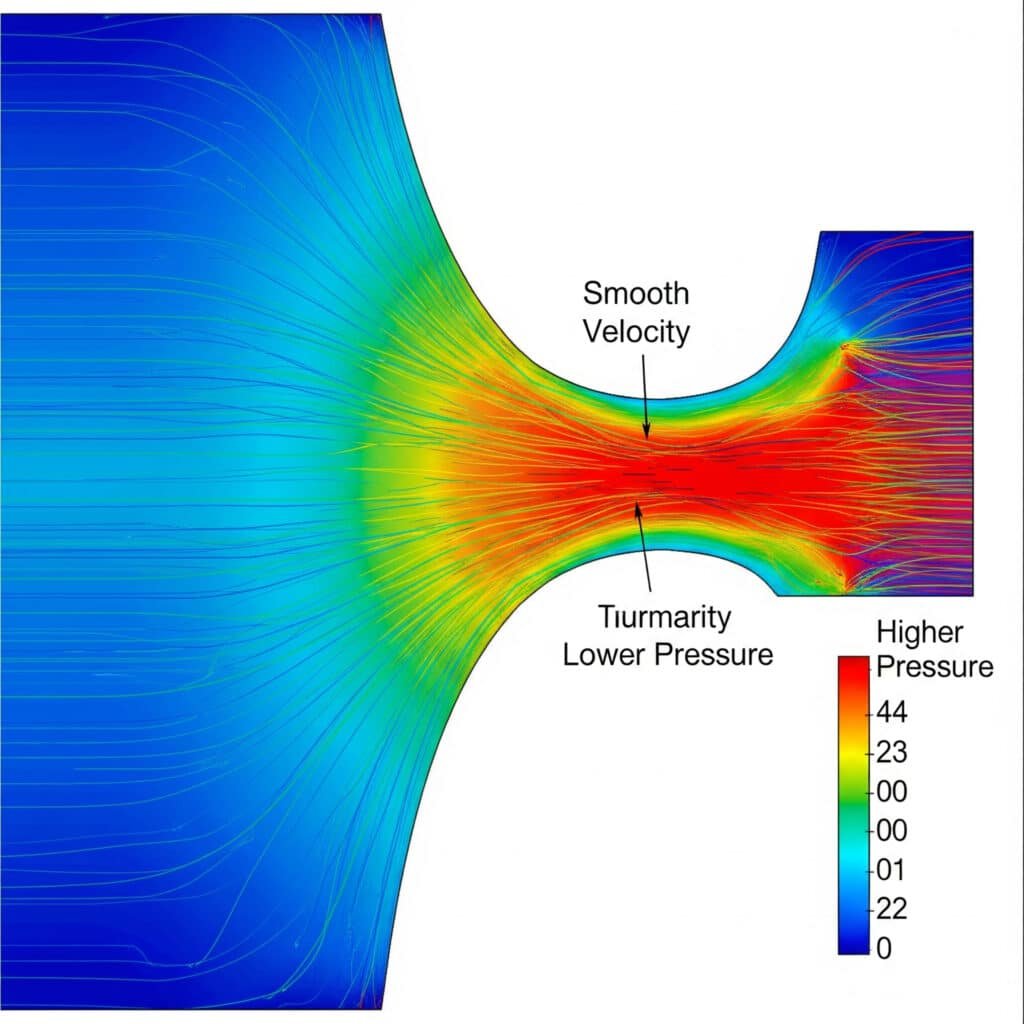
Problemele de curgere a gazelor îi costă pe producători miliarde de dolari anual în pierderi de energie și defecțiuni ale sistemelor. Inginerii aplică adesea principiile curgerii lichidelor la sistemele de gaze, ceea ce duce la erori de calcul catastrofale. Înțelegerea principiilor de curgere a gazelor previne erorile de proiectare costisitoare și pericolele pentru siguranță.
Principiul curgerii gazelor este guvernat de ecuația continuității, conservarea impulsului și conservarea energiei, unde viteza, presiunea, densitatea și temperatura gazelor interacționează prin curgere compresibilă1 ecuații fundamental diferite de curgerea lichidelor incompresibile.
În urmă cu doi ani, am lucrat cu un inginer chimist britanic pe nume Sarah Thompson, al cărui sistem de distribuție a gazelor naturale prezenta fluctuații periculoase de presiune. Echipa ei folosea calcule de debit incompresibil pentru un debit de gaz compresibil. După implementarea principiilor corecte de curgere a gazelor, am eliminat fluctuațiile de presiune și am redus consumul de energie cu 35%.
Tabla de conținut
- Care sunt principiile fundamentale care guvernează curgerea gazelor?
- Cum diferă ecuațiile curgerii compresibile de curgerea lichidelor?
- Ce factori influențează comportamentul debitului de gaze în sistemele industriale?
- Cum interacționează presiunea, temperatura și viteza în curgerea gazelor?
- Care sunt diferitele tipuri de regimuri de curgere a gazelor?
- Cum să calculați și să optimizați debitul de gaz în aplicații industriale?
- Concluzie
- Întrebări frecvente despre principiile de curgere a gazelor
Care sunt principiile fundamentale care guvernează curgerea gazelor?
Curgerea gazelor funcționează în conformitate cu trei legi fundamentale de conservare care guvernează toate mișcările fluidelor, dar cu caracteristici unice datorate compresibilității gazelor și variațiilor de densitate.
Principiile curgerii gazelor se bazează pe conservarea masei (ecuația continuității), conservarea impulsului (a doua lege a lui Newton) și conservarea energiei (prima lege a termodinamicii), modificate pentru comportamentul fluidelor compresibile.
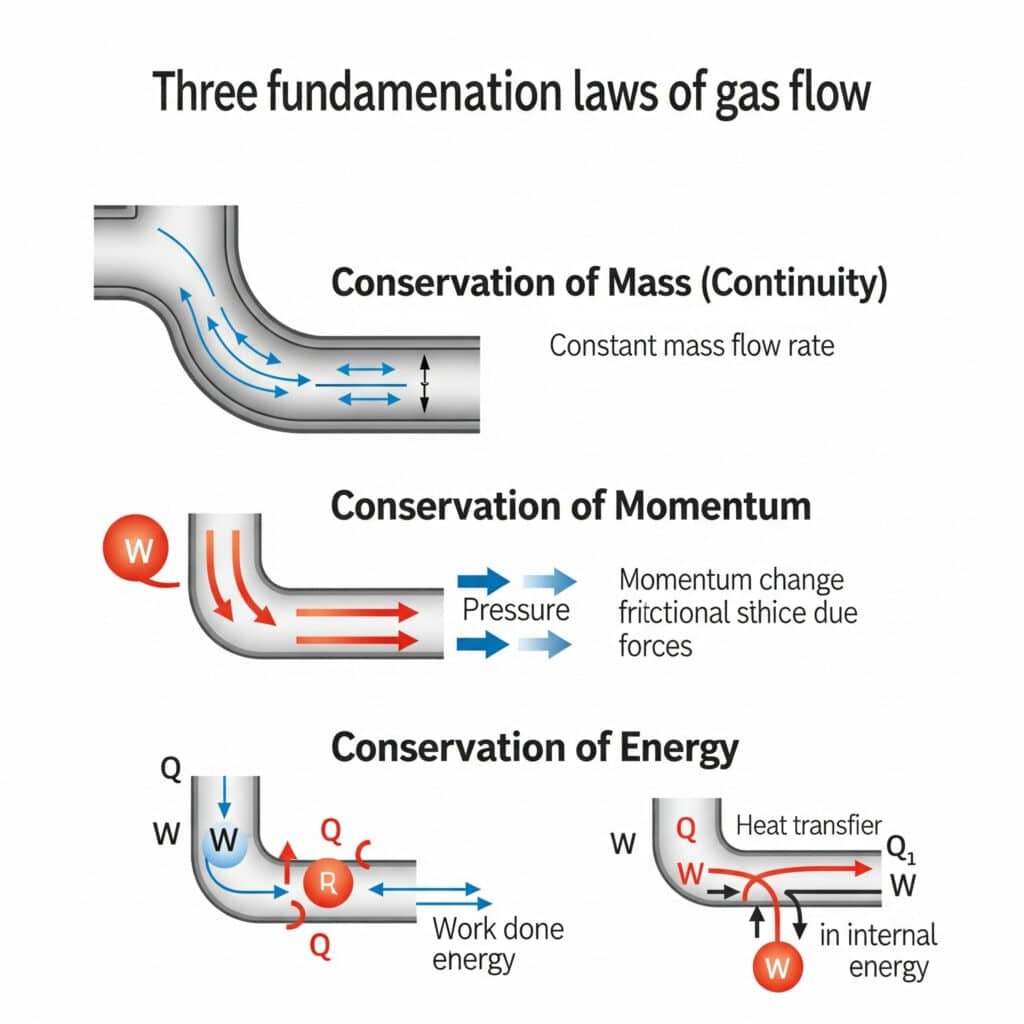
Conservarea masei (ecuația de continuitate)
Spre deosebire de lichidele incompresibile, ecuația de continuitate pentru curgerea gazelor ține cont de modificările de densitate care apar din cauza variațiilor de presiune și temperatură.
Ecuația de continuitate a debitului de gaz:
∂ρ/∂t + ∇-(ρV) = 0
Pentru un debit constant: ρ₁A₁V₁ = ρ₂A₂V₂
Unde:
- ρ = Densitatea gazului (variază în funcție de presiune și temperatură)
- A = Suprafața secțiunii transversale
- V = Viteza gazului
- t = timp
Implicații cheie:
- Densitatea gazului se modifică în funcție de presiune și temperatură
- Debitul masic rămâne constant în curgere constantă
- Viteza crește pe măsură ce densitatea scade
- Modificările de suprafață afectează atât viteza, cât și densitatea
Conservarea momentului motor
Conservarea momentului în curgerea gazelor ia în considerare forțele de presiune, forțele vâscoase și forțele corpului care acționează asupra fluidului compresibil.
Ecuația momentului (Navier-Stokes2):
ρ(∂V/∂t + V-∇V) = -∇p + μ∇²V + ρg
Pentru aplicații cu debit de gaz:
- Termenul gradientului de presiune domină în curgerea la viteză mare
- Efecte vâscoase importante în apropierea pereților și în curgerea laminară
- Efectele compresibilității devin semnificative peste Mach 0,3
Conservarea energiei
Conservarea energiei pentru curgerea gazului include energia cinetică, energia potențială, energia internă și lucrul de curgere, ținând seama de schimbările de temperatură datorate comprimării și dilatării.
Ecuația energiei:
h + V²/2 + gz = constantă (de-a lungul liniei de curent)
Unde:
- h = entalpie specifică (include energia internă și lucrul de curgere)
- V²/2 = Energia cinetică pe unitatea de masă
- gz = energie potențială pe unitate de masă
Considerații energetice:
| Forma de energie | Impactul debitului de gaz | Magnitudinea tipică |
|---|---|---|
| Energia cinetică | Semnificativ la viteze mari | V²/2 |
| Energie de presiune | Dominantă în majoritatea aplicațiilor | p/ρ |
| Energie internă | Se modifică odată cu temperatura | CᵥT |
| Fluxul de lucru | Necesar pentru mișcarea gazului | pv |
Ecuația de stat
Debitul de gaz necesită o ecuație de stare pentru a relaționa presiunea, densitatea și temperatura, de obicei legea gazului ideal pentru majoritatea aplicațiilor industriale.
Legea gazului ideal:
p = ρRT
Unde:
- p = presiune absolută
- ρ = Densitatea gazului
- R = Constanta specifică a gazului
- T = temperatura absolută
Pentru gazele reale, pot fi necesare ecuații de stare mai complexe, cum ar fi ecuațiile van der Waals sau Redlich-Kwong.
Cum diferă ecuațiile curgerii compresibile de curgerea lichidelor?
Curgerea gazelor compresibile prezintă un comportament fundamental diferit de curgerea lichidelor incompresibile, necesitând metode de analiză și considerente de proiectare specializate.
Curgerea compresibilă diferă prin variații de densitate, limitări ale vitezei sonice, formarea undelor de șoc și cuplarea temperatură-presiune care nu apar în sistemele de curgere a lichidelor incompresibile.
Efectele variației densității
Densitatea gazului se modifică semnificativ în funcție de presiune și temperatură, afectând modelele de curgere, distribuția vitezei și cerințele de proiectare a sistemului.
Impactul schimbării densității:
- Viteza Accelerația: Gazul accelerează pe măsură ce se dilată
- Cădere de presiune: Relații neliniare presiune-debit
- Efectele temperaturii: Densitate invers proporțională cu temperatura
- Flux înecat: Limitări ale debitului maxim
Viteza sonică și numărul Mach
Comportamentul debitului de gaz se schimbă dramatic pe măsură ce viteza se apropie de viteza sunetului, creând limitări critice de proiectare care nu sunt prezente în sistemele cu lichide.
Calcularea vitezei sonice:
a = √(γRT)
Unde:
- a = viteza sunetului în gaz
- γ = Raportul de căldură specifică (Cp/Cv)
- R = Constanta specifică a gazului
- T = temperatura absolută
Numărul Mach3 Semnificație:
M = V/a (Raportul vitezei la viteza sonică)
| Gama Mach | Regimul de curgere | Caracteristici |
|---|---|---|
| M < 0.3 | Incompresibil | Densitate practic constantă |
| 0.3 < M < 1.0 | Subsonic Compresibil | Modificări semnificative ale densității |
| M = 1.0 | Sonic | Condiții critice de curgere |
| M > 1.0 | Supersonic | Sunt posibile unde de șoc |
Fenomenul fluxului înecat
Flux înecat4 apare atunci când viteza gazului atinge condiții sonice, limitând debitul maxim indiferent de reducerea presiunii din aval.
Condiții de debit înfundat:
- Debit masic maxim atins
- Modificările presiunii din aval nu afectează debitul din amonte
- Raportul presiunii critice: p₂/p₁ ≈ 0,53 pentru aer
- Frecvente în duze, orificii și supape de control
Cuplaj temperatură-presiune
Fluxul de gaze implică schimbări semnificative de temperatură datorate expansiunii și comprimării, afectând performanța și proiectarea sistemului.
Procese termodinamice:
- Curgere izentropică: Proces reversibil, adiabatic
- Flux izoterm: Temperatură constantă (curgere lentă cu transfer de căldură)
- Flux adiabatic: Nu există transfer de căldură (curgere rapidă)
- Fluxul politropic: Caz general cu transfer de căldură
Ce factori influențează comportamentul debitului de gaze în sistemele industriale?
Factorii multipli influențează comportamentul fluxului de gaze în aplicațiile industriale, necesitând o analiză cuprinzătoare pentru proiectarea și funcționarea corectă a sistemului.
Factorii cheie includ proprietățile gazului, geometria sistemului, condițiile de funcționare, efectele transferului de căldură și frecarea pereților care determină în mod colectiv modelele de curgere, căderile de presiune și performanța sistemului.
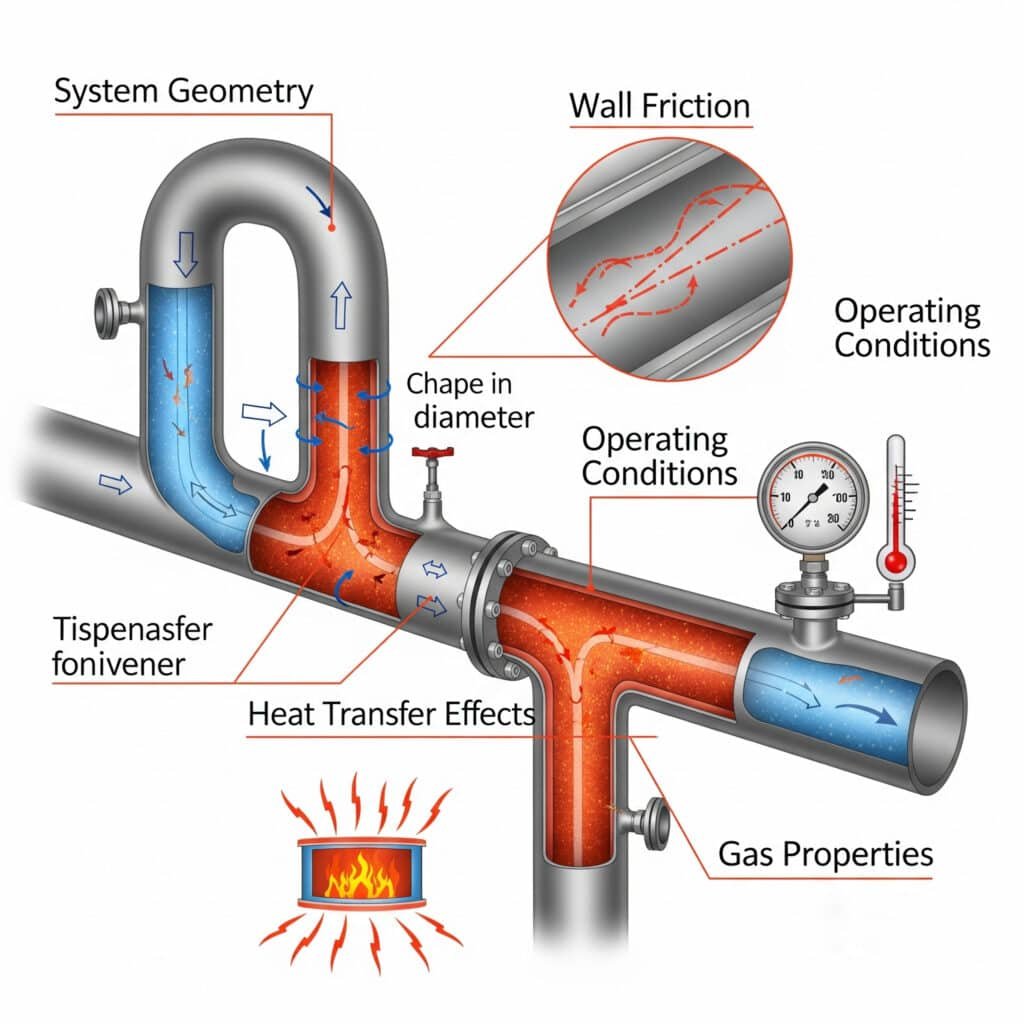
Impactul proprietăților gazelor
Diferitele gaze prezintă caracteristici de curgere diferite în funcție de proprietățile lor moleculare, raporturile de căldură specifică și comportamentul termodinamic.
Proprietăți critice ale gazelor:
| Proprietate | Simbol | Impactul asupra fluxului | Valori tipice |
|---|---|---|---|
| Raportul de căldură specifică | γ | Viteza sonică, expansiunea | 1,4 (aer), 1,3 (CO₂) |
| Constantă de gaz | R | Relația densitate-presiune | 287 J/kg-K (aer) |
| Vâscozitate | μ | Pierderi prin frecare | 1,8×10-⁵ Pa-s (aer) |
| Greutatea moleculară | M | Densitatea în condiții date | 29 kg/kmol (aer) |
Efectele geometriei sistemului
Diametrul conductei, lungimea, fitingurile și modificările suprafeței de curgere afectează în mod semnificativ modelele de curgere a gazelor și pierderile de presiune.
Considerații geometrice:
- Diametrul țevii: Afectează viteza și pierderile prin frecare
- Lungime: Determină pierderea totală de presiune prin frecare
- Modificări de zonă: Creați efecte de accelerare/decelerare
- Fitinguri: Cauzează pierderi locale de presiune
- Rugozitatea suprafeței: Influențează factorul de frecare
Presiunea și temperatura de funcționare
Condițiile de funcționare ale sistemului afectează în mod direct densitatea gazului, vâscozitatea și comportamentul de curgere prin intermediul relațiilor termodinamice.
Efectele condițiilor de funcționare:
- Presiune ridicată: Crește densitatea, reduce efectele compresibilității
- Presiune scăzută: Scade densitatea, crește viteza
- Temperatură ridicată: Reduce densitatea, crește viteza sonică
- Temperatură scăzută: Crește densitatea, poate provoca condens
Efectele transferului de căldură
Adăugarea sau îndepărtarea căldurii în timpul curgerii gazului afectează semnificativ distribuția temperaturii, densității și presiunii.
Scenarii de transfer termic:
- Încălzire: Crește temperatura, reduce densitatea, accelerează curgerea
- Răcire: Scade temperatura, crește densitatea, încetinește curgerea
- Adiabatic: Nu există transfer de căldură, temperatura se modifică datorită expansiunii/compresiei
- Izotermic: Temperatură constantă menținută prin transfer de căldură
Impactul fricțiunii peretelui
Frecarea dintre gaz și pereții conductei creează pierderi de presiune și afectează profilurile de viteză, deosebit de importante în cazul conductelor lungi.
Calcularea pierderii prin frecare:
Δp = f × (L/D) × (ρV²/2)
Unde:
- f = factor de frecare (funcție de numărul Reynolds și de rugozitate)
- L = Lungimea conductei
- D = Diametrul conductei
- ρ = Densitatea gazului
- V = Viteza gazului
Cum interacționează presiunea, temperatura și viteza în curgerea gazelor?
Interacțiunea dintre presiune, temperatură și viteză în fluxul de gaze creează relații complexe care trebuie înțelese pentru proiectarea și analiza corectă a sistemului.
Interacțiunile dintre fluxurile de gaze urmează relații termodinamice în care schimbările de presiune afectează temperatura și densitatea, schimbările de viteză afectează presiunea prin efectele momentului, iar schimbările de temperatură afectează toate celelalte proprietăți prin ecuația de stare.
Relațiile presiune-viteză
Viteza și presiunea gazului sunt invers legate prin ecuația lui Bernoulli modificată pentru curgerea compresibilă, creând provocări unice de proiectare.
Ecuația Bernoulli modificată pentru curgerea gazelor:
∫dp/ρ + V²/2 + gz = constantă
Pentru gazul ideal: γ/(γ-1) × (p/ρ) + V²/2 = constantă
Efectele presiune-viteză:
- Cădere de presiune: Cauzează creșterea vitezei datorită expansiunii gazului
- Creșterea vitezei: Poate provoca o scădere suplimentară a presiunii prin efecte de moment
- Accelerare: Apare în mod natural pe măsură ce gazul se dilată prin sistem
- Decelerare: Necesită creșterea presiunii sau extinderea suprafeței
Cuplaj temperatură-viteză
Temperatura și viteza gazului sunt cuplate prin conservarea energiei, schimbările de temperatură afectând proprietățile gazului și comportamentul debitului.
Relațiile temperatură-viteză:
T₀ = T + V²/(2Cp)
Unde:
- T₀ = Temperatura de stagnare (totală)
- T = Temperatura statică
- V = Viteza gazului
- Cp = căldură specifică la presiune constantă
Implicații practice:
- Fluxul de gaz de mare viteză reduce temperatura statică
- Temperatura de stagnare rămâne constantă în cazul unui flux adiabatic
- Modificările de temperatură afectează densitatea și vâscozitatea gazului
- Răcirea poate provoca condensarea anumitor gaze
Efecte presiune-temperatură
Presiunea și temperatura interacționează prin ecuația de stare și procesele termodinamice, afectând densitatea gazului și caracteristicile debitului.
Relații termodinamice de proces:
| Tip proces | Relația presiune-temperatură | Aplicație |
|---|---|---|
| Isentropic | p/p₀ = (T/T₀)^(γ/(γ-1)) | Duze, difuzoare |
| Izotermic | pV = constant, T = constant | Curgere lentă cu transfer de căldură |
| Isobaric | p = constantă | Încălzire cu presiune constantă |
| Izocoric | V = constant | Încălzire cu volum constant |
Variații ale densității
Densitatea gazului variază atât cu presiunea, cât și cu temperatura, în conformitate cu legea gazului ideal, creând un comportament complex al curgerii.
Calculul densității:
ρ = p/(RT)
Efectele densității asupra debitului:
- Densitate ridicată: Viteză mai mică pentru un debit masic dat
- Densitate redusă: Viteză mai mare, efecte potențiale de compresibilitate
- Gradiente de densitate: Creați efecte de flotabilitate și de amestecare
- Modificări ale densității: Afectează momentul și transferul de energie
Recent, am ajutat un inginer american specializat în gaze naturale, pe nume Robert Chen, din Texas, să-și optimizeze sistemul de conducte. Ținând cont în mod corespunzător de interacțiunile temperatură-presiune-velocitate, am redus energia de pompare cu 28%, în timp ce capacitatea de transport a crescut cu 15%.
Care sunt diferitele tipuri de regimuri de curgere a gazelor?
Fluxul de gaz prezintă diferite regimuri bazate pe viteză, condiții de presiune și geometria sistemului, fiecare dintre acestea necesitând metode de analiză și considerații de proiectare specifice.
Regimurile de curgere a gazelor includ curgerea laminară, turbulentă, subsonică, sonică și supersonică, fiecare caracterizată prin diferite profile de viteză, relații de presiune și caracteristici de transfer termic.
Curgere laminară vs. curgere turbulentă
Tranzițiile fluxului de gaze de la laminar la turbulent se bazează pe Numărul Reynolds5, care afectează pierderile de presiune, transferul de căldură și caracteristicile de amestecare.
Numărul Reynolds pentru curgerea gazului:
Re = ρVD/μ
Unde:
- ρ = Densitatea gazului (variază în funcție de presiune și temperatură)
- V = Viteza medie
- D = Diametrul conductei
- μ = Vâscozitatea dinamică
Clasificări ale regimului de curgere:
| Numărul Reynolds | Regimul de curgere | Caracteristici |
|---|---|---|
| Re < 2300 | Laminar | Curgere lină, previzibilă |
| 2300 < Re < 4000 | Tranziția | Comportament instabil, mixt |
| Re > 4000 | Turbulent | Amestec haotic, îmbunătățit |
Regimul fluxului subsonic
Fluxul subsonic apare atunci când viteza gazului este mai mică decât viteza locală a sunetului, permițând perturbărilor de presiune să se propage în amonte.
Caracteristicile fluxului subsonic:
- Numărul Mach: M < 1.0
- Propagarea presiunii: Perturbațiile se deplasează în amonte
- Controlul debitului: Condițiile din aval afectează întregul sistem
- Modificări ale densității: Moderat, variații previzibile
- Flexibilitate de proiectare: Soluții multiple posibile
Aplicații de curgere subsonică:
- Majoritatea sistemelor de distribuție a gazelor industriale
- Sisteme HVAC și de ventilație
- Sisteme pneumatice de joasă presiune
- Echipamente pentru procese chimice
- Manipularea gazelor din centralele electrice
Flux sonic (flux înecat)
Fluxul sonic apare atunci când viteza gazului este egală cu viteza locală a sunetului, creând condiții critice de curgere cu caracteristici unice.
Proprietăți Sonic Flow:
- Numărul Mach: M = 1.0 exact
- Debit masic maxim: Nu poate fi depășită
- Independența presiunii: Presiunea din aval nu afectează debitul
- Raport de presiune critică: De obicei în jur de 0,53 pentru aer
- Efectele temperaturii: Scădere semnificativă a temperaturii
Aplicații Sonic Flow:
- Duze pentru turbine cu gaz
- Supape de siguranță
- Dispozitive de măsurare a debitului
- Duze pentru motoare de rachetă
- Regulatoare de gaz de înaltă presiune
Regimul fluxului supersonic
Curgerea supersonică are loc atunci când viteza gazului depășește viteza sunetului, creând unde de șoc și fenomene de curgere unice.
Caracteristicile fluxului supersonic:
- Numărul Mach: M > 1.0
- Undele de șoc: Schimbări bruște de presiune și temperatură
- Direcția debitului: Informația nu poate călători în amonte
- Valuri de expansiune: Reduceri ușoare ale presiunii
- Complexitatea proiectării: Necesită o analiză specializată
Tipuri de unde de șoc:
| Tip șoc | Caracteristici | Aplicații |
|---|---|---|
| Șoc normal | Perpendicular la flux | Difuzoare, intrări |
| Șoc oblic | Înclinat în direcția de curgere | Avioane supersonice |
| Ventilator de expansiune | Reducerea treptată a presiunii | Designul duzei |
Flux hiperspațial
Curgerea hiperspațială are loc la numere de Mach foarte mari (de obicei M > 5), unde efectele suplimentare devin importante.
Efecte hiperspațiale:
- Efecte reale ale gazului: Legea gazului ideal este încălcată
- Reacții chimice: Disocierea și ionizarea
- Transfer de căldură: Efecte extreme de încălzire
- Efecte vâscoase: Interacțiuni ale stratului limită
Cum să calculați și să optimizați debitul de gaz în aplicații industriale?
Calculele debitului de gaz necesită metode specializate care să țină cont de efectele compresibilității, în timp ce optimizarea se concentrează pe minimizarea consumului de energie și maximizarea performanței sistemului.
Calculele debitului de gaz utilizează ecuațiile debitului compresibil, corelațiile factorului de frecare și relațiile termodinamice, în timp ce optimizarea implică dimensionarea conductelor, selectarea nivelului de presiune și configurarea sistemului pentru a minimiza costurile energetice.
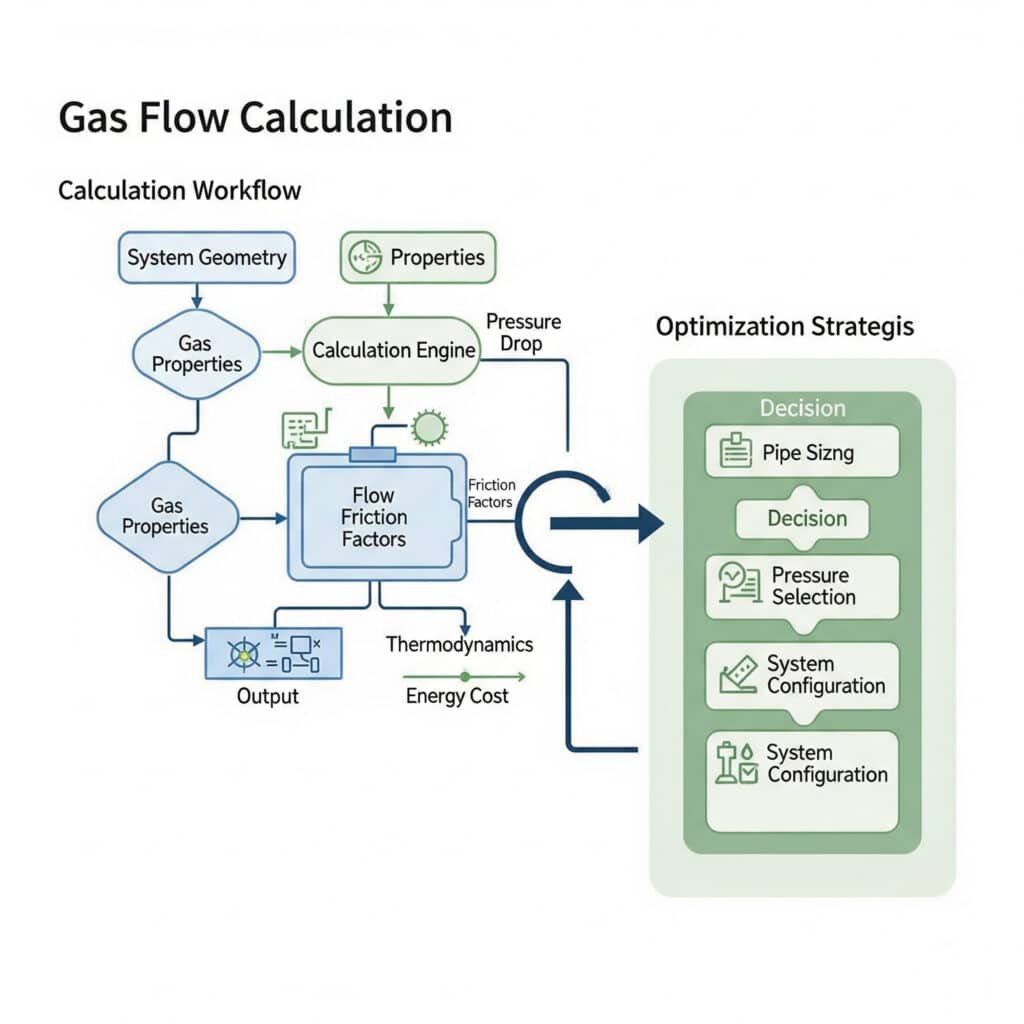
Calcule de bază ale debitului de gaz
Calculele fluxului de gaze încep cu ecuațiile fundamentale modificate pentru efectele fluxului compresibil și proprietățile reale ale gazelor.
Calcularea debitului masic:
ṁ = ρAV = (p/RT)AV
Pentru un debit strangulat printr-un orificiu:
ṁ = CdA√(γρp)[2/(γ+1)]^((γ+1)/(2(γ-1)))
Unde:
- Cd = Coeficient de descărcare
- A = Suprafața orificiului
- γ = Raportul de căldură specifică
- ρ = Densitatea în amonte
- p = presiunea din amonte
Calculul căderilor de presiune
Calculele pierderilor de sarcină pentru debitul de gaz trebuie să ia în considerare efectele de accelerare datorate expansiunii gazului, pe lângă pierderile prin frecare.
Componentele pierderii totale de presiune:
- Picătură de presiune de frecare: Din cauza tensiunii de forfecare a peretelui
- Accelerare Cădere de presiune: Din cauza creșterii vitezei
- Elevare Pierdere de presiune: Datorită efectelor gravitaționale
- Cădere de presiune a racordului: Din cauza perturbațiilor fluxului
Formula picăturii de presiune de frecare:
Δpf = f(L/D)(ρV²/2)
Cădere de presiune la accelerare:
Δpa = ρ₂V₂² - ρ₁V₁² (pentru schimbări de zonă)
Analiza fluxului conductei
Analiza conductelor lungi necesită calcule iterative din cauza modificării proprietăților gazului pe lungimea conductei.
Etapele calculării conductei:
- Divizarea conductei: În segmente cu proprietăți constante
- Calcularea proprietăților segmentului: Presiune, temperatură, densitate
- Determinarea regimului de curgere: Laminar sau turbulent
- Calculați căderea de presiune: Pentru fiecare segment
- Actualizarea proprietăților: Pentru segmentul următor
- Iterate: Până la atingerea convergenței
Ecuația simplificată a conductei:
p₁² - p₂² = (fLṁ²RT)/(A²Dρ₀)
Unde:
- p₁, p₂ = presiuni de intrare și de ieșire
- f = factor de frecare mediu
- L = lungimea conductei
- ṁ = Debit masic
- R = Constanta gazului
- T = Temperatura medie
- A = Suprafața conductei
- D = Diametrul conductei
- ρ₀ = Densitatea de referință
Strategii de optimizare a sistemului
Optimizarea sistemului de flux de gaze echilibrează costurile de capital, costurile de exploatare și cerințele de performanță pentru a obține un cost minim al ciclului de viață.
Parametrii de optimizare:
| Parametru | Impactul asupra sistemului | Strategia de optimizare |
|---|---|---|
| Diametrul țevii | Costul de capital vs. scăderea presiunii | Calculul diametrului economic |
| Presiunea de funcționare | Costul compresiei vs. costul conductei | Optimizarea nivelului de presiune |
| Etapizarea compresorului | Eficiență vs. complexitate | Optimizarea numărului de etape |
| Dimensiunea schimbătorului de căldură | Recuperarea căldurii vs. costul de capital | Schimb de căldură economic |
Dimensionarea economică a conductelor
Dimensionarea economică a conductei echilibrează costul de capital al conductei cu costurile energetice de pompare pe durata de viață a sistemului.
Formula diametrului economic:
D_economic = K(ṁ/ρ)^0.37
În cazul în care K depinde de:
- Costul energiei
- Costul conductei
- Durata de viață a sistemului
- Rata dobânzii
- Ore de funcționare pe an
Măsurarea și controlul debitului
Măsurarea și controlul precis al debitului de gaz necesită înțelegerea efectelor fluxului compresibil asupra dispozitivelor de măsurare.
Considerații privind măsurarea debitului:
- Plăci cu orificii: Necesită corecții de compresibilitate
- Contoare Venturi: Mai puțin sensibil la compresibilitate
- Contoare cu turbină: Afectat de modificările densității gazului
- Contoare cu ultrasunete: Necesită compensarea temperaturii
- Contoare Coriolis: Măsurarea directă a debitului masic
Dinamica computațională a fluidelor (CFD)
Sistemele complexe de curgere a gazelor beneficiază de analiza CFD pentru a optimiza performanța și a prezice comportamentul în diferite condiții de funcționare.
Aplicații CFD:
- Geometrii complexe: Forme neregulate și fitinguri
- Transfer de căldură: Curgere combinată și analiză termică
- Analiza amestecului: Variații ale compoziției gazului
- Optimizare: Studii privind parametrii de proiectare
- Rezolvarea problemelor: Identificarea problemelor de flux
Am lucrat recent cu un inginer petrochimic canadian pe nume David Wilson din Alberta, a cărui instalație de prelucrare a gazelor avea probleme de eficiență. Utilizând analiza CFD combinată cu calcule adecvate ale fluxului de gaze, am identificat zonele de recirculare care provocau o risipă de energie de 20%. După implementarea modificărilor de proiectare, consumul de energie a scăzut cu 18%, crescând în același timp capacitatea de prelucrare.
Concluzie
Principiile curgerii gazelor guvernează comportamentul fluidelor compresibile prin legi de conservare modificate pentru variațiile densității, necesitând metode de analiză specializate care să ia în considerare interacțiunile presiune-temperatură-velocitate și efectele compresibilității, fundamental diferite de sistemele de curgere a lichidelor.
Întrebări frecvente despre principiile de curgere a gazelor
Care este principiul fundamental al curgerii gazelor?
Curgerea gazului funcționează pe baza conservării masei, momentului și energiei, modificate pentru comportamentul fluidului compresibil în care densitatea gazului variază în funcție de presiune și temperatură, creând interacțiuni viteză-presiune-temperatură.
Prin ce diferă curgerea gazelor de curgerea lichidelor?
Curgerea gazelor implică schimbări semnificative de densitate, limitări ale vitezei sonice, cuplaj temperatură-presiune și fenomene de curgere înecată care nu apar în sistemele de curgere a lichidelor incompresibile.
Ce este debitul înecat în sistemele de gaz?
Debitul strangulat apare atunci când viteza gazului atinge condiții sonice (Mach = 1,0), limitând debitul masic maxim indiferent de reducerea presiunii din aval, ceea ce se întâmplă frecvent în duze și supape de control.
Cum se calculează debitul de gaz?
Calculul debitului de gaz utilizează ecuația ṁ = ρAV, unde densitatea variază cu presiunea și temperatura conform legii gazului ideal, necesitând soluții iterative pentru sistemele complexe.
Ce factori afectează comportamentul fluxului de gaze?
Factorii cheie includ proprietățile gazului (greutate moleculară, raport de căldură specifică), geometria sistemului (diametrul conductei, fitinguri), condițiile de funcționare (presiune, temperatură) și efectele transferului de căldură.
De ce este important numărul Mach în curgerea gazelor?
Numărul Mach (viteza / viteza sonică) determină caracteristicile regimului de curgere: curgerea subsonică (M1) generează unde de șoc.
-
Explică diferența fundamentală dintre curgerea compresibilă, în care densitatea fluidului se modifică semnificativ în funcție de presiune, și curgerea incompresibilă, în care densitatea este considerată constantă, o distincție esențială între dinamica gazelor și a lichidelor. ↩
-
Oferă o prezentare generală a ecuațiilor Navier-Stokes, un set de ecuații cu derivate parțiale care stau la baza mecanicii fluidelor, descriind mișcarea substanțelor fluide vâscoase pe baza conservării momentului. ↩
-
Oferă o definiție detaliată a numărului Mach, o mărime adimensională în dinamica fluidelor care reprezintă raportul dintre viteza de curgere dincolo de o limită și viteza locală a sunetului și care este utilizată pentru a clasifica regimurile de curgere. ↩
-
Descrie fenomenul debitului strangulat, o condiție limită a debitului compresibil în care debitul masic nu va crește la o scădere suplimentară a presiunii din aval, deoarece viteza în punctul cel mai îngust a atins viteza sunetului. ↩
-
Explică numărul Reynolds, o mărime adimensională esențială în mecanica fluidelor utilizată pentru a prezice tiparele de curgere, ajutând la distingerea între regimurile de curgere laminară (lină) și turbulentă (haotică). ↩



