Inginerii se confruntă cu confuzii atunci când calculează volumele pentru componentele sferice aplatizate în sistemele de cilindri pneumatici fără tijă. Calculele incorecte ale volumelor conduc la calcule greșite ale presiunii și la defecțiuni ale sistemului.
O sferă plană (sferoid aplatizat) are volumul V = (4/3)πa²b, unde "a" este raza ecuatorială și "b" este raza polară, frecvent întâlnită în acumulator pneumatic1 și aplicații de amortizare.
Luna trecută, l-am ajutat pe Andreas, un inginer proiectant din Germania, al cărui sistem pneumatic de amortizare a eșuat pentru că a folosit volumul sferei standard în loc de calculele sferoidului aplatizat pentru camerele sale de acumulare aplatizate.
Tabla de conținut
- Ce este o sferă plată în aplicațiile pneumatice?
- Cum se calculează volumul sferei plate?
- Unde sunt utilizate sferele plate în cilindrii fără tijă?
- Cum afectează aplatizarea volumul și performanța?
Ce este o sferă plată în aplicațiile pneumatice?
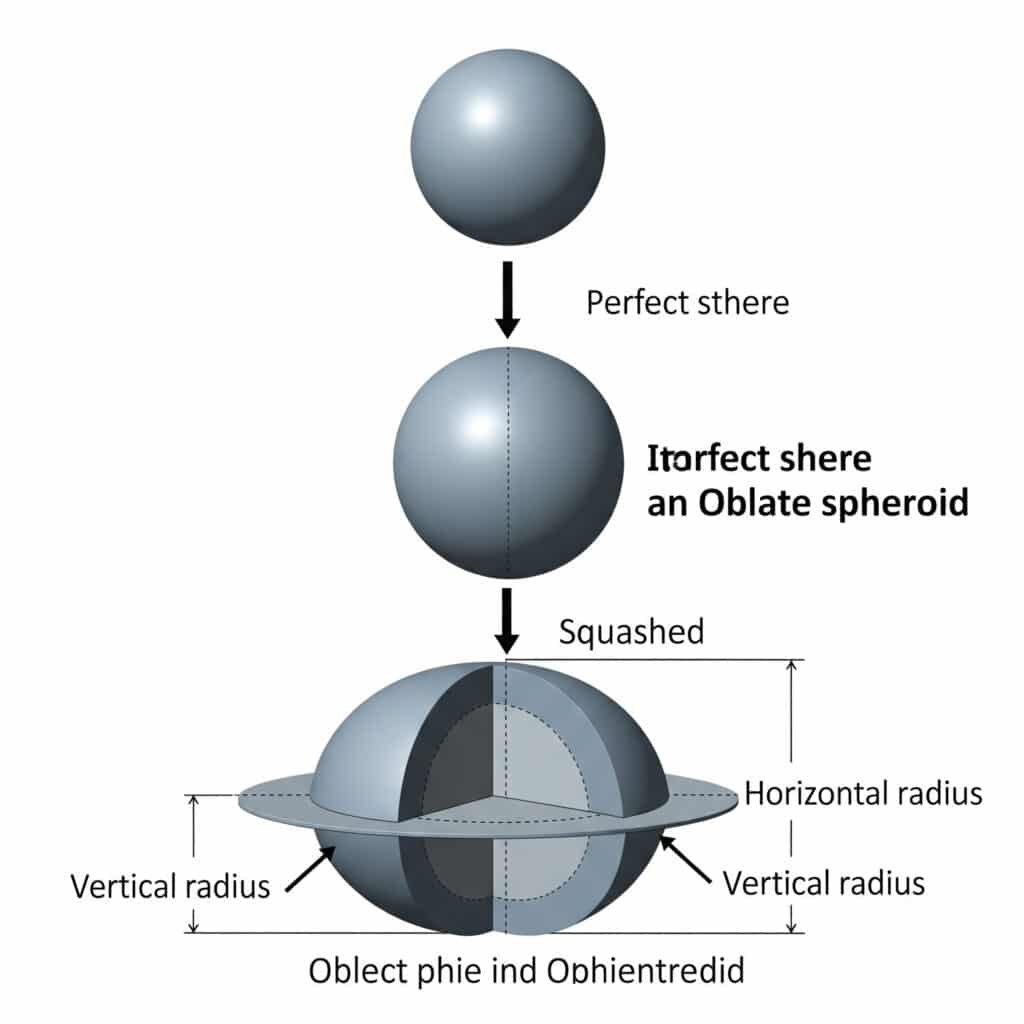
O sferă plată, denumită tehnic sferoid oblic2, este o formă tridimensională creată atunci când o sferă este comprimată de-a lungul unei axe, utilizată în mod obișnuit în modelele de acumulatori și amortizoare pneumatice.
O sferă plată rezultă din aplatizarea unei sfere perfecte de-a lungul axei sale verticale, creând o secțiune transversală eliptică cu măsurători diferite ale razei orizontale și verticale.
Definiție geometrică
Caracteristici de formă
- Sferoid oblat: Termen tehnic geometric
- Sferă aplatizată: Descriere industrială comună
- Profil eliptic: Vedere în secțiune transversală
- Simetrie rotațională: În jurul axei verticale
Dimensiuni cheie
- Raza ecuatorială (a): Raza orizontală (mai mare)
- Raza polară (b): Raza verticală (mai mică)
- Raportul de aplatizare: b/a < 1.0
- Raportul de aspect: Raportul dintre înălțime și lățime
Sferă plată vs Sferă perfectă
| Caracteristică | Sfera perfectă | Sferă plată |
|---|---|---|
| Formă | Raza uniformă | Comprimat pe verticală |
| Formula volumului | (4/3)πr³ | (4/3)πa²b |
| Secțiune transversală | Cerc | Elipsă |
| Simetrie | Toate direcțiile | Numai orizontal |
Ratele comune de aplatizarea
Aplatizarea luminii
- Raportul: b/a = 0,8-0,9
- Aplicații: Ușoare constrângeri de spațiu
- Impactul asupra volumului: 10-20% reducere
- Performanță: Efect minim
Aplatizare moderată
- Raportul: b/a = 0,6-0,8
- Aplicații: Modele standard de acumulatori
- Impactul asupra volumului: 20-40% reducere
- Performanță: Modificări de presiune vizibile
Aplatizarea grea
- Raportul: b/a = 0,3-0,6
- Aplicații: Limitări severe ale spațiului
- Impactul asupra volumului: 40-70% reducere
- Performanță: Considerații semnificative privind proiectarea
Aplicații pneumatice
Camere de acumulare
Întâlnesc sfere plate în:
- Instalații cu spațiu limitat: Limitări de înălțime
- Proiecte integrate: Construite în cadrele mașinilor
- Aplicații personalizate: Cerințe specifice privind volumul
- Proiecte de modernizare: Amenajarea spațiilor existente
Sisteme de amortizare
- Amortizarea la sfârșit de cursă: Aplicații pentru cilindri fără tijă
- Absorbția șocurilor: Gestionarea încărcăturii de impact
- Reglarea presiunii: Control de funcționare fără probleme
- Reducerea zgomotului: Funcționare mai silențioasă a sistemului
Considerații privind fabricarea
Metode de producție
- Desen adânc: Formarea tablelor metalice
- Hidroformare: Proces de modelare de precizie
- Prelucrare: Componente personalizate unice
- Turnare: Producție de volum mare
Selectarea materialului
- Oțel: Aplicații de înaltă presiune
- Aluminiu: Proiecte sensibile la greutate
- Oțel inoxidabil: Medii corozive
- Materiale compozite: Cerințe specializate
Cum se calculează volumul sferei plate?
Calculul volumului sferei plate necesită formula sferoidului oblic, utilizând atât măsurătorile razei ecuatoriale, cât și cele ale razei polare, pentru o proiectare precisă a sistemului pneumatic.
Utilizați formula V = (4/3)πa²b unde "a" este raza ecuatorială (orizontală) și "b" este raza polară (verticală) pentru a calcula cu precizie volumul sferei plate.
Defalcarea formulei volumului
Formula standard
V = (4/3)πa²b
- V: Volumul în unități cubice
- π: 3.14159 (constantă matematică)
- a: Raza ecuatorială (orizontală)
- b: Raza polară (verticală)
- 4/3: Coeficientul de volum al sferoidului
Componente ale formulei
- Zona ecuatorială: πa² (secțiune transversală orizontală)
- Scalarea polară: factor b (compresie verticală)
- Coeficient de volum: 4/3 (constantă geometrică)
- Unități de rezultat: Potriviți unitățile de rază de intrare cubate
Calcul pas cu pas
Procesul de măsurare
- Măsurarea diametrului ecuatorial: Cea mai largă dimensiune orizontală
- Calculați raza ecuatorială: a = diametru ÷ 2
- Măsurarea diametrului polar: Dimensiunea verticală a înălțimii
- Calculați raza polară: b = înălțime ÷ 2
- Aplicați formula: V = (4/3)πa²b
Exemplu de calcul
Pentru un acumulator pneumatic:
- Diametrul ecuatorial: 100mm → a = 50mm
- Diametrul polar: 60mm → b = 30mm
- Volum: V = (4/3)π(50)²(30)
- Rezultat: V = (4/3)π(2500)(30) = 314,159 mm³
Exemple de calcul al volumului
| Raza ecuatorială | Raza polară | Raport de aplatizare | Volum | Comparație cu Sfera |
|---|---|---|---|---|
| 50mm | 50mm | 1.0 | 523,599 mm³ | 100% (sferă perfectă) |
| 50mm | 40mm | 0.8 | 418,879 mm³ | 80% |
| 50mm | 30mm | 0.6 | 314,159 mm³ | 60% |
| 50mm | 20mm | 0.4 | 209,440 mm³ | 40% |
Instrumente de calcul
Calcul manual
- Calculator științific: Cu funcția π
- Verificarea formulei: Verificarea de două ori a intrărilor
- Consistența unității: Menținerea acelorași unități pe tot parcursul
- Precizie: Calculați cu zecimalele corespunzătoare
Instrumente digitale
- Software de inginerie: Calcule de volum CAD
- Calculatoare online: Instrumente sferoid oblate
- Formule pentru foaie de calcul: Calcule automatizate
- Aplicații mobile: Instrumente de calcul pe teren
Erori comune de calcul
Greșeli de măsurare
- Raza vs diametru: Utilizarea dimensiunii greșite
- Confuzia axei: Amestecarea măsurătorilor orizontale/verticale
- Inconsecvența unității: mm vs inch amestecare
- Pierdere de precizie: Rotunjire prea devreme
Erori de formulă
- Formulă greșită: Utilizarea sferei în loc de sferoid
- Inversarea parametrilor: Schimbarea valorilor a și b
- Greșeli de coeficient: Lipsește factorul 4/3
- Aproximarea π: Utilizarea 3.14 în loc de 3.14159
Metode de verificare
Tehnici de verificare încrucișată
- Software CAD: Calcularea volumului modelului 3D
- Deplasarea apei: Măsurarea fizică a volumului
- Calcule multiple: Compararea diferitelor metode
- Specificații ale producătorului: Date privind volumul publicat
Verificări ale rezonabilității
- Reducerea volumului: Ar trebui să fie mai puțin decât sfera perfectă
- Aplatizarea corelației: Mai multă aplatizare = mai puțin volum
- Verificarea unității: Rezultatele corespund magnitudinii așteptate
- Adecvarea aplicației: Volumul îndeplinește cerințele sistemului
Când am ajutat-o pe Maria, un proiectant de sisteme pneumatice din Spania, să calculeze volumele acumulatorilor pentru instalația sa de cilindri fără tijă, am descoperit că calculele sale inițiale foloseau formule de sferă în loc de sferoid oblic, rezultând o supraestimare a volumului 35% și o performanță inadecvată a sistemului.
Unde sunt utilizate sferele plate în cilindrii fără tijă?
Sferele plate apar în diverse componente ale cilindrilor pneumatici fără tijă, unde constrângerile de spațiu necesită optimizarea volumului, menținând în același timp funcționalitatea vasului sub presiune.
Sferele plate sunt utilizate în mod obișnuit în camere de acumulator, sisteme de amortizare și recipiente sub presiune integrate în ansambluri de cilindri fără tijă, unde restricțiile de înălțime limitează modelele sferice standard.
Aplicații pentru acumulator
Acumulatoare integrate
- Optimizarea spațiului: Încadrare în cadrele mașinilor
- Eficiența volumului: Depozitare maximă la o înălțime limitată
- Stabilitatea presiunii: Funcționare fără probleme în timpul vârfurilor de cerere
- Integrarea sistemului: Integrat în bazele de montare a cilindrilor
Instalații de modernizare
- Utilaje existente: Limitări ale înălțimii
- Proiecte de modernizare: Adăugarea acumulării la sistemele mai vechi
- Constrângeri de spațiu: Lucrul în limitele concepției inițiale
- Îmbunătățirea performanței: Răspuns îmbunătățit al sistemului
Sisteme de amortizare
Amortizarea la sfârșit de cursă
Eu instalez amortizare sferă plată pentru:
- Cilindri magnetici fără tijă: Decelerare lină
- Cilindri fără tijă ghidați: Reducerea impactului
- Cilindri fără tijă cu acțiune dublă: Amortizare bidirecțională
- Aplicații de mare viteză: Absorbția șocurilor
Reglarea presiunii
- Netezirea fluxului: Eliminați vârfurile de presiune
- Reducerea zgomotului: Funcționare mai silențioasă
- Protecția componentelor: Uzură și stres reduse
- Stabilitatea sistemului: Performanță consecventă
Componente specializate
Recipiente sub presiune
- Aplicații personalizate: Cerințe de spațiu unice
- Modele multifuncționale: Depozitare și montare combinate
- Sisteme modulare: Configurații stivuibile
- Acces pentru întreținere: Modele în stare de funcționare
Camere de senzori
- Monitorizarea presiunii: Sisteme integrate de măsurare
- Detectarea debitului: Aplicații de detectare a vitezei
- Diagnosticarea sistemului: Monitorizarea performanței
- Sisteme de siguranță: Integrarea descărcării de presiune
Considerații privind proiectarea
Constrângeri de spațiu
| Aplicație | Limita de înălțime | Aplatizare tipică | Impactul volumului |
|---|---|---|---|
| Montaj sub pardoseală | 50mm | b/a = 0,3 | Reducere 70% |
| Integrarea mașinilor | 100mm | b/a = 0,6 | Reducere 40% |
| Aplicații retrofit | 150mm | b/a = 0,8 | Reducere 20% |
| Montaj standard | 200mm+ | b/a = 0,9 | Reducere 10% |
Cerințe de performanță
- Presiune nominală: Menținerea integrității structurale
- Capacitatea volumului: Satisface cererea sistemului
- Caracteristicile debitului: Dimensiuni adecvate ale intrării/ieșirii
- Acces pentru întreținere: Considerații privind serviceability
Exemple de instalare
Mașini de ambalare
- Aplicație: Echipament de umplere de mare viteză
- Constrângere: 40mm spațiu liber pe înălțime
- Soluție: Acumulator puternic aplatizat (b/a = 0,25)
- Rezultat: 75% reducerea volumului, performanță adecvată
Montaj auto
- Aplicație: Sistem de poziționare robotizat
- Constrângere: Integrare în baza roboților
- Soluție: Aplatizarea moderată (b/a = 0,7)
- Rezultat: 30% economie de spațiu, performanță menținută
Prelucrarea alimentelor
- Aplicație: Sistem de cilindru sanitar fără tijă
- Constrângere: Autorizare pentru mediu de spălare
- Soluție: Design personalizat cu sferă plată
- Rezultat: Clasificare IP69K3 cu volum optimizat
Specificații de fabricație
Dimensiuni standard
- Mic: 50mm ecuatorial, diferite dimensiuni polare
- Mediu: 100mm ecuatorial, variații de înălțime
- Mare: 200mm ecuatorial, dimensiuni polare personalizate
- Personalizat: Dimensiuni specifice aplicației
Opțiuni materiale
- Oțel carbon: Aplicații de presiune standard
- Oțel inoxidabil: Medii corozive
- Aluminiu: Instalații sensibile la greutate
- Compozit: Cerințe specializate
Anul trecut, am lucrat cu Thomas, un constructor de mașini din Elveția, care avea nevoie de stocare a acumulatorilor pentru linia sa compactă de ambalare. Acumulatorii sferici standard nu se potriveau restricției de înălțime de 60 mm, așa că am proiectat acumulatori cu sferă plată cu raportul b/a = 0,4, obținând 60% din volumul inițial și respectând toate constrângerile de spațiu.
Cum afectează aplatizarea volumul și performanța?
Aplatizarea reduce semnificativ capacitatea de volum, afectând în același timp dinamica presiunii, caracteristicile debitului și performanța generală a sistemului în aplicațiile pneumatice fără tijă.
Fiecare creștere cu 10% a aplatizării (scăderea raportului b/a) reduce volumul cu aproximativ 10% și afectează răspunsul la presiune, modelele de curgere și eficiența sistemului în aplicațiile cu acumulator pneumatic.
Analiza impactului volumului
Relațiile de reducere a volumului
Raportul volumului = (b/a) pentru sferoizi oblici
- Relație liniară: Volumul scade proporțional cu aplatizarea
- Impact previzibil: Ușor de calculat modificările de volum
- Flexibilitate de proiectare: Alegeți raportul optim de aplatizare
- Compromisuri de performanță: Echilibrul spațiu vs capacitate
Modificări de volum cuantificate
| Raportul de aplatizare (b/a) | Retenția volumului | Pierderea de volum | Capacitatea de aplicare |
|---|---|---|---|
| 0.9 | 90% | 10% | Excelentă |
| 0.8 | 80% | 20% | Foarte bun |
| 0.7 | 70% | 30% | Bun |
| 0.6 | 60% | 40% | Corect |
| 0.5 | 50% | 50% | Slabă |
| 0.4 | 40% | 60% | Foarte slabă |
Efectele performanței presiunii
Caracteristici de răspuns la presiune
- Volum redus: Schimbări de presiune mai rapide
- Sensibilitate mai mare: Mai receptiv la variațiile de debit
- Creșterea ciclismului: Cicluri de încărcare/descărcare mai frecvente
- Instabilitatea sistemului: Oscilații ale presiunii potențiale
Ajustări pentru calculul presiunii
P₁V₁ = P₂V₂ (Legea lui Boyle4 se aplică)
- Volum mai mic: Presiune mai mare pentru aceeași masă de aer
- Variații de presiune: Variații mai mari în timpul funcționării
- Dimensionarea sistemului: Compensarea cu o capacitate mai mare a compresorului
- Marje de siguranță: Cerințe sporite privind presiunea nominală
Caracteristici de debit
Modificări ale modelului de flux
- Creșterea turbulenței: Forma aplatizată creează perturbări ale fluxului
- Scădere de presiune: Rezistență mai mare datorită camerelor deformate
- Efecte de intrare/ieșire: Poziționarea porturilor devine critică
- Viteza de curgere: Viteze crescute prin secțiuni restricționate
Impactul debitului
- Suprafață efectivă redusă: Apar restricții de debit
- Pierderi de presiune: Eficiența energetică scade
- Timp de răspuns: Ratele de umplere/descărcare mai lente
- Performanța sistemului: Reducerea eficienței globale
Considerații structurale
Distribuția tensiunilor
- Tensiuni concentrate: Sarcini mai mari în zonele aplatizate
- Grosimea materialului: Poate necesita consolidare
- Rezistența la oboseală5: Potențial redus al ciclului de viață
- Factori de siguranță: Sunt necesare marje de proiectare mai mari
Presiunea nominală Efecte
| Raport de aplatizare | Creșterea stresului | Factor de siguranță recomandat | Grosimea materialului |
|---|---|---|---|
| 0.9 | 10% | 1.5 | Standard |
| 0.8 | 25% | 1.8 | +10% |
| 0.7 | 45% | 2.0 | +20% |
| 0.6 | 70% | 2.5 | +35% |
Optimizarea performanței sistemului
Strategii de compensare
- Cantitate crescută a acumulatorului: Mai multe unități mai mici
- Funcționare la presiune mai mare: Compensarea pierderii de volum
- Design îmbunătățit al debitului: Optimizarea configurațiilor de intrare/ieșire
- Reglarea sistemului: Reglați parametrii de control
Monitorizarea performanței
- Frecvența ciclurilor de presiune: Monitorizarea stabilității sistemului
- Măsurarea debitului: Verificarea capacității adecvate
- Efectele temperaturii: Verificați dacă încălzirea este excesivă
- Intervale de întreținere: Ajustare pe baza performanței
Orientări privind proiectarea
Selecția optimă a aplatizării
- b/a > 0,8: Impact minim asupra performanței
- b/a = 0,6-0,8: Acceptabil pentru majoritatea aplicațiilor
- b/a = 0,4-0,6: Necesită o proiectare atentă a sistemului
- b/a < 0,4: În general, nu se recomandă
Recomandări specifice aplicației
- Ciclism de înaltă frecvență: Minimizarea aplatizării (b/a > 0,7)
- Instalații critice pentru spațiu: Acceptarea compromisurilor de performanță
- Sisteme de siguranță critice: Rapoarte de aplatizare conservatoare
- Proiecte sensibile la costuri: Echilibrul performanță vs economie de spațiu
Date de performanță din lumea reală
Rezultatele studiului de caz
Când am analizat datele de performanță de la 50 de instalații cu diferite rapoarte de aplatizare:
- 10% aplatizarea: Impact neglijabil asupra performanței
- 30% aplatizarea: 15% creșterea frecvenței ciclismului
- 50% aplatizarea: 40% reducerea capacității efective
- Aplatizarea 70%: Instabilitatea sistemului în 60% din cazuri
Optimizarea succesului
Pentru Elena, un integrator de sisteme din Italia, am optimizat designul acumulatorului cu cilindru fără tijă prin limitarea aplatizării la b/a = 0,75, obținând o economie de spațiu de 25%, menținând în același timp 95% din performanța sistemului original și eliminând problemele de instabilitate a presiunii.
Concluzie
Volumul sferei plate utilizează formula V = (4/3)πa²b cu raza ecuatorială "a" și raza polară "b". Aplatizarea reduce proporțional volumul, dar afectează răspunsul la presiune și caracteristicile de curgere în aplicațiile pneumatice.
Întrebări frecvente despre volumul sferei plate
Care este formula pentru volumul sferei plate?
Formula volumului sferei plate (sferoid oblic) este V = (4/3)πa²b, unde "a" este raza ecuatorială (orizontală) și "b" este raza polară (verticală). Aceasta diferă de formula unei sfere perfecte V = (4/3)πr³.
Cât volum se pierde la aplatizarea unei sfere?
Pierderea de volum este egală cu raportul de aplatizare. Dacă raza polară este de 70% din raza ecuatorială (b/a = 0,7), volumul devine 70% din volumul sferei inițiale, reprezentând o reducere de volum de 30%.
Unde sunt utilizate sferele plate în sistemele pneumatice?
Sferele plate sunt utilizate în camere de acumulatori, sisteme de amortizare și recipiente sub presiune, unde restricțiile de înălțime limitează modelele sferice standard. Aplicațiile obișnuite includ integrarea utilajelor cu spațiu limitat și instalațiile de modernizare.
Cum afectează aplatizarea performanța pneumatică?
Aplatizarea reduce capacitatea de volum, crește sensibilitatea la presiune și creează turbulențe de curgere. Sistemele cu acumulatori puternic aplatizați (b/a < 0,6) pot prezenta instabilitate a presiunii și eficiență redusă, ceea ce necesită o compensare a proiectului.
Care este raportul maxim de aplatizare recomandat?
Pentru aplicațiile pneumatice, mențineți raporturile de aplatizare peste b/a = 0,6 pentru o performanță acceptabilă. Rapoartele sub 0,4 cauzează, în general, instabilitatea sistemului și necesită modificări semnificative de proiectare pentru a menține o funcționare adecvată.
-
Înțelegerea funcției și scopului acumulatoarelor pneumatice în sistemele de alimentare cu fluide. ↩
-
Aflați definiția matematică și proprietățile geometrice ale unui sferoid oblic. ↩
-
Consultați definiția oficială și cerințele de testare pentru gradul de protecție IP69K. ↩
-
Revedeți principiile legii lui Boyle, care descrie relația dintre presiune și volum într-un gaz. ↩
-
Explorați conceptul de rezistență la oboseală și modul în care materialele se comportă în condiții de încărcare ciclică. ↩



