Инженеры сталкиваются с путаницей при расчете объема сплюснутых сферических компонентов в системах бесштоковых пневматических цилиндров. Неправильные расчеты объема приводят к ошибкам в расчете давления и сбоям в работе системы.
Плоская сфера (продолговатый сфероид) имеет объем V = (4/3)πa²b, где "a" - экваториальный радиус, а "b" - полярный радиус, обычно встречается в пневматический аккумулятор1 и амортизации.
В прошлом месяце я помогал Андреасу, инженеру-конструктору из Германии, чья система пневматической амортизации вышла из строя из-за того, что он использовал стандартный объем сферы вместо расчетов продолговатого сфероида для своих сплющенных аккумуляторных камер.
Оглавление
- Что такое плоская сфера в пневматических системах?
- Как рассчитать объем плоской сферы?
- Где используются плоские сферы в бесштоковых цилиндрах?
- Как плоское покрытие влияет на объем и производительность?
Что такое плоская сфера в пневматических системах?
Плоская сфера, технически называемая продолговатый сфероид2Трехмерная форма, создаваемая при сжатии сферы вдоль одной оси, широко используется в пневматических аккумуляторах и амортизаторах.
Плоская сфера получается в результате сплющивания идеальной сферы вдоль вертикальной оси, образуя эллиптическое сечение с различными горизонтальными и вертикальными радиусами.
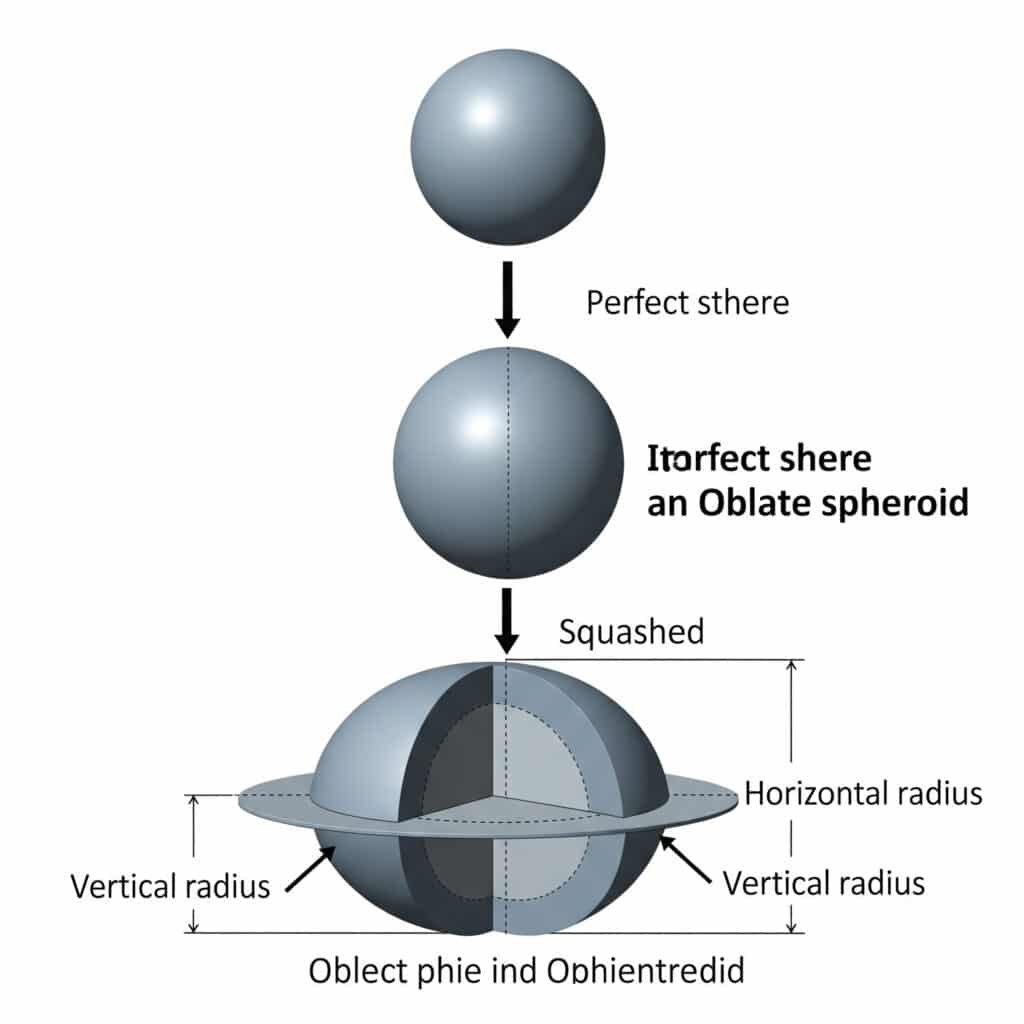
Геометрическое определение
Характеристики формы
- Обильный сфероид: Технический геометрический термин
- Сплющенная сфера: Общее описание промышленности
- Эллиптический профиль: Вид в поперечном сечении
- Вращательная симметрия: Вокруг вертикальной оси
Основные размеры
- Экваториальный радиус (a): Горизонтальный радиус (больше)
- Полярный радиус (b): Вертикальный радиус (меньше)
- Коэффициент сплющивания: б/г < 1,0
- Соотношение сторон: Отношение высоты к ширине
Плоская сфера против идеальной сферы
| Характеристика | Идеальная сфера | Плоская сфера |
|---|---|---|
| Форма | Равномерный радиус | Сжатие по вертикали |
| Формула объема | (4/3)πr³ | (4/3)πa²b |
| Поперечное сечение | Круг | Эллипс |
| Симметрия | Все направления | Только горизонтально |
Распространенные коэффициенты сплющивания
Сплющивание света
- Соотношение: b/a = 0,8-0,9
- Приложения: Небольшие ограничения по площади
- Влияние объема: 10-20% снижение
- Производительность: Минимальный эффект
Умеренное сглаживание
- Соотношение: b/a = 0,6-0,8
- Приложения: Стандартные конструкции аккумуляторов
- Влияние объема: 20-40% снижение
- Производительность: Заметные изменения давления
Сильное сплющивание
- Соотношение: b/a = 0,3-0,6
- Приложения: Серьезные ограничения по площади
- Влияние объема: 40-70% редукция
- Производительность: Важные аспекты проектирования
Пневматические приложения
Аккумуляторные камеры
Я сталкиваюсь с плоскими сферами:
- Установки с ограниченным пространством: Ограничения по высоте
- Интегрированные конструкции: Встроенные в рамы машин
- Пользовательские приложения: Особые требования к объему
- Проекты модернизации: Оснащение существующих помещений
Амортизационные системы
- Демпфирование в конце хода: Применение бесштоковых цилиндров
- Амортизация: Управление ударной нагрузкой
- Регулировка давления: Плавное управление
- Снижение шума: Более тихая работа системы
Производственные соображения
Методы производства
- Глубокий рисунок: Обработка листового металла
- Гидроформовка: Прецизионный процесс формования
- Обработка: Индивидуальные компоненты
- Кастинг: Крупносерийное производство
Выбор материала
- Сталь: Применение при высоком давлении
- Алюминий: Конструкции, чувствительные к весу
- Нержавеющая сталь: Коррозионные среды
- Композитные материалы: Специализированные требования
Как рассчитать объем плоской сферы?
Для точного расчета объема плоской сферы требуется формула для продолговатого сфероида с использованием измерений экваториального и полярного радиусов для точного проектирования пневматической системы.
Используйте формулу V = (4/3)πa²b, где "a" - экваториальный радиус (горизонтальный), а "b" - полярный радиус (вертикальный), чтобы точно рассчитать объем плоской сферы.
Разбивка формулы объема
Стандартная формула
V = (4/3)πa²b
- V: Объем в кубических единицах
- π: 3.14159 (математическая константа)
- a: Экваториальный радиус (горизонтальный)
- b: Полярный радиус (вертикальный)
- 4/3: Коэффициент объема сфероида
Компоненты формулы
- Экваториальная зона: πa² (горизонтальное сечение)
- Полярное масштабирование: b-фактор (вертикальное сжатие)
- Коэффициент объема: 4/3 (геометрическая константа)
- Единицы измерения результата: Соответствие входного радиуса единицам в кубе
Пошаговый расчет
Процесс измерения
- Измерьте экваториальный диаметр: Самый широкий горизонтальный размер
- Рассчитайте экваториальный радиус: a = диаметр ÷ 2
- Измерьте полярный диаметр: Вертикальный размер по высоте
- Рассчитайте полярный радиус: b = высота ÷ 2
- Нанести формулу: V = (4/3)πa²b
Пример расчета
Для пневматического аккумулятора:
- Экваториальный диаметр: 100 мм → a = 50 мм
- Полярный диаметр: 60 мм → b = 30 мм
- Объем: V = (4/3)π(50)²(30)
- Результат: V = (4/3)π(2500)(30) = 314,159 мм³
Примеры расчета объема
| Экваториальный радиус | Полярный радиус | Коэффициент сплющивания | Объем | Сравнение со сферой |
|---|---|---|---|---|
| 50 мм | 50 мм | 1.0 | 523 599 мм³ | 100% (идеальная сфера) |
| 50 мм | 40 мм | 0.8 | 418 879 мм³ | 80% |
| 50 мм | 30 мм | 0.6 | 314 159 мм³ | 60% |
| 50 мм | 20 мм | 0.4 | 209 440 мм³ | 40% |
Инструменты расчета
Ручной расчет
- Научный калькулятор: С функцией π
- Проверка формулы: Дважды проверьте вводимые данные
- Консистенция единицы: Поддерживайте одинаковые единицы измерения во всем
- Точность: Вычислить с точностью до десятичных знаков
Цифровые инструменты
- Инженерное программное обеспечение: Расчеты объема CAD
- Онлайн-калькуляторы: Инструменты сфероида
- Формулы электронных таблиц: Автоматизированные расчеты
- Мобильные приложения: Инструменты для полевых расчетов
Распространенные ошибки в расчетах
Ошибки при измерении
- Радиус против диаметра: Использование неправильного размера
- Путаница вокруг оси: Смешивание горизонтальных и вертикальных измерений
- Несоответствие единиц измерения: мм против дюймов
- Потеря точности: Слишком раннее округление
Ошибки в формулах
- Неправильная формула: Использование сферы вместо сфероида
- Изменение параметров: Поменяйте местами значения a и b
- Коэффициент ошибок: Отсутствие фактора 4/3
- π-аппроксимация: Использование 3.14 вместо 3.14159
Методы проверки
Методы перекрестной проверки
- Программное обеспечение CAD: Расчет объема 3D-модели
- Вытеснение воды: Измерение физического объема
- Множественные расчеты: Сравнение различных методов
- Технические характеристики производителя: Опубликованные данные об объеме
Проверки разумности
- Уменьшение объема: Должна быть менее чем идеальная сфера
- Плоская корреляция: Больше сплющивания = меньше объема
- Проверка прибора: Результаты соответствуют ожидаемой величине
- Пригодность для применения: Том соответствует системным требованиям
Когда я помогал Марии, проектировщице пневматических систем из Испании, рассчитать объем аккумуляторов для ее установки без штока, мы обнаружили, что в ее первоначальных расчетах использовались формулы сферы, а не продолговатого сфероида, что привело к завышению объема на 35% и неадекватной производительности системы.
Где используются плоские сферы в бесштоковых цилиндрах?
Плоские сферы используются в различных компонентах бесштоковых пневматических цилиндров, где ограниченное пространство требует оптимизации объема при сохранении функциональности сосуда под давлением.
Плоские сферы обычно используются в аккумуляторных камерах, системах амортизации и встроенных сосудах давления в блоках бесштоковых цилиндров, где ограничения по высоте ограничивают стандартные сферические конструкции.
Применение аккумуляторов
Встроенные аккумуляторы
- Оптимизация пространства: Вписываются в рамки машин
- Эффективность объема: Максимальное хранение при ограниченной высоте
- Стабильность давления: Бесперебойная работа во время пиков спроса
- Системная интеграция: Встраивается в монтажные основания цилиндров
Установки для модернизации
- Существующее оборудование: Ограничения по высоте
- Проекты модернизации: Добавление накоплений в старые системы
- Ограничения по площади: Работа в рамках первоначального проекта
- Улучшение производительности: Улучшенный отклик системы
Амортизационные системы
Демпфирование в конце хода
Я устанавливаю плоскую амортизацию для сферы:
- Магнитные бесштоковые цилиндры: Плавное замедление
- Направляемые бесштоковые цилиндры: Снижение воздействия
- Бесштоковые цилиндры двойного действия: Двунаправленная амортизация
- Высокоскоростные приложения: Амортизация
Регулирование давления
- Сглаживание потока: Устранение скачков давления
- Снижение шума: Более тихая работа
- Защита компонентов: Снижение износа и напряжения
- Стабильность системы: Постоянная производительность
Специализированные компоненты
Сосуды под давлением
- Пользовательские приложения: Уникальные требования к пространству
- Многофункциональные конструкции: Комбинированное хранение и монтаж
- Модульные системы: Возможность штабелирования
- Доступ для технического обслуживания: Исправные конструкции
Сенсорные камеры
- Контроль давления: Интегрированные измерительные системы
- Обнаружение потока: Применение датчиков скорости
- Диагностика системы: Мониторинг производительности
- Системы безопасности: Интеграция в систему сброса давления
Конструктивные соображения
Ограничения пространства
| Приложение | Ограничение по высоте | Типичное сплющивание | Влияние объема |
|---|---|---|---|
| Монтаж под полом | 50 мм | b/a = 0,3 | Уменьшение 70% |
| Интеграция машин | 100 мм | b/a = 0,6 | Уменьшение 40% |
| Модернизация | 150 мм | b/a = 0,8 | уменьшение 20% |
| Стандартный монтаж | 200 мм+ | b/a = 0,9 | Снижение 10% |
Требования к производительности
- Номинальное давление: Поддерживать структурную целостность
- Объемная емкость: Удовлетворяйте потребности системы
- Характеристики потока: Адекватный размер входного/выходного отверстия
- Доступ для технического обслуживания: Соображения, связанные с эксплуатацией
Примеры установки
Упаковочное оборудование
- Приложение: Высокоскоростное фасовочное оборудование
- Ограничение: 40-миллиметровый зазор по высоте
- Решение: Сильно сплющенный аккумулятор (b/a = 0,25)
- Результат: 75% снижение громкости, адекватная производительность
Автомобильная сборка
- Приложение: Роботизированная система позиционирования
- Ограничение: Интеграция в базу роботов
- Решение: Умеренное уплощение (b/a = 0,7)
- Результат: 30% экономия места, сохранение производительности
Пищевая промышленность
- Приложение: Санитарная система цилиндров без штока
- Ограничение: Допуск к промывочной среде
- Решение: Индивидуальный дизайн плоской сферы
- Результат: Степень защиты IP69K3 с оптимизированным объемом
Производственные характеристики
Стандартные размеры
- Маленький: 50 мм экваториальные, различные полярные размеры
- Средний: 100 мм экваториальный, колебания высоты
- Большой: 200-миллиметровый экваториал, индивидуальный полярный размер
- Пользовательское: Размеры для конкретного применения
Варианты материалов
- Углеродистая сталь: Стандартное применение под давлением
- Нержавеющая сталь: Коррозионные среды
- Алюминий: Установки, чувствительные к весу
- Композит: Специализированные требования
В прошлом году я работал с Томасом, машиностроителем из Швейцарии, которому требовались аккумуляторы для его компактной упаковочной линии. Стандартные сферические аккумуляторы не вписывались в ограничение по высоте 60 мм, поэтому мы разработали аккумуляторы в виде плоской сферы с соотношением b/a = 0,4, что позволило получить 60% первоначального объема при соблюдении всех ограничений по площади.
Как плоское покрытие влияет на объем и производительность?
Сплющивание значительно снижает объемную емкость, влияя на динамику давления, характеристики потока и общую производительность системы в бесштоковых пневматических системах.
Каждое увеличение сплющивания (уменьшение отношения b/a) на 10% уменьшает объем примерно на 10% и влияет на реакцию давления, характер потока и эффективность системы в пневматических аккумуляторах.
Анализ воздействия на объем
Соотношения уменьшения объема
Соотношение объемов = (b/a) для продолговатых сфероидов
- Линейная зависимость: Объем уменьшается пропорционально уплощению
- Предсказуемое воздействие: Легко рассчитать изменения объема
- Гибкость конструкции: Выберите оптимальный коэффициент сплющивания
- Компромиссы в производительности: Баланс пространства и вместимости
Количественные изменения объема
| Коэффициент сплющивания (b/a) | Сохранение объема | Потеря объема | Пригодность для применения |
|---|---|---|---|
| 0.9 | 90% | 10% | Превосходно |
| 0.8 | 80% | 20% | Очень хорошо |
| 0.7 | 70% | 30% | Хорошо |
| 0.6 | 60% | 40% | Ярмарка |
| 0.5 | 50% | 50% | Бедный |
| 0.4 | 40% | 60% | Очень плохо |
Влияние давления на производительность
Характеристики отклика на давление
- Уменьшение объема: Более быстрое изменение давления
- Повышенная чувствительность: Более чутко реагирует на изменения потока
- Увеличение количества велосипедов: Более частые циклы заряда/разряда
- Нестабильность системы: Колебания потенциального давления
Корректировки расчета давления
P₁V₁ = P₂V₂ (Закон Бойля4 применяется)
- Меньший объем: Более высокое давление для той же массы воздуха
- Скачки давления: Большие колебания во время работы
- Определение размеров системы: Компенсировать за счет большей производительности компрессора
- Пределы безопасности: Повышенные требования к номинальному давлению
Характеристики потока
Изменения схемы потока
- Увеличение турбулентности: Плоская форма создает возмущения потока
- Перепад давления: Повышенное сопротивление благодаря деформированным камерам
- Эффекты на входе/выходе: Позиционирование порта становится критическим
- Скорость потока: Увеличение скорости на ограниченных участках
Влияние скорости потока
- Уменьшение эффективной площади: Возникают ограничения потока
- Потери давления: Снижение энергоэффективности
- Время отклика: Замедленная скорость наполнения/разрядки
- Производительность системы: Общее снижение эффективности
Структурные соображения
Распределение напряжений
- Концентрированные стрессы: Повышенная нагрузка на плоские участки
- Толщина материала: Может потребоваться усиление
- Усталостная прочность5: Потенциал сокращенного срока службы
- Факторы безопасности: Необходимо увеличить маржу при проектировании
Влияние номинального давления
| Коэффициент сплющивания | Повышение стресса | Рекомендуемый коэффициент безопасности | Толщина материала |
|---|---|---|---|
| 0.9 | 10% | 1.5 | Стандарт |
| 0.8 | 25% | 1.8 | +10% |
| 0.7 | 45% | 2.0 | +20% |
| 0.6 | 70% | 2.5 | +35% |
Оптимизация производительности системы
Компенсационные стратегии
- Увеличенное количество аккумуляторов: Несколько мелких единиц
- Работа при повышенном давлении: Компенсируйте потерю объема
- Улучшенная конструкция потока: Оптимизация конфигурации входов и выходов
- Настройка системы: Настройка параметров управления
Мониторинг производительности
- Частота цикличности давления: Контроль стабильности системы
- Измерения скорости потока: Убедитесь в достаточной пропускной способности
- Температурные эффекты: Проверьте, нет ли чрезмерного нагрева
- Интервалы технического обслуживания: Корректировка в зависимости от производительности
Руководство по проектированию
Оптимальный выбор сплющивания
- b/a > 0,8: Минимальное влияние на производительность
- b/a = 0,6-0,8: Приемлемо для большинства применений
- b/a = 0,4-0,6: Требует тщательного проектирования системы
- b/a < 0,4: Обычно не рекомендуется
Рекомендации по применению
- Высокочастотная цикличность: Минимизация уплощения (b/a > 0,7)
- Установки, критичные для космического пространства: Примите компромиссные решения по производительности
- Критические системы безопасности: Консервативные коэффициенты сплющивания
- Проекты, чувствительные к затратам: Баланс между производительностью и экономией пространства
Данные о производительности в реальных условиях
Результаты тематического исследования
Когда я проанализировал данные о производительности 50 установок с различными коэффициентами сплющивания:
- 10% сплющивание: Незначительное влияние на производительность
- 30% сплющивание: 15% увеличение частоты велосипедных прогулок
- 50% сплющивание: 40% снижение эффективной мощности
- 70% сплющивание: Нестабильность системы в 60% случаев
Успех оптимизации
Для Елены, системного интегратора из Италии, мы оптимизировали конструкцию бесштокового цилиндрического аккумулятора, ограничив сплющивание до b/a = 0,75, что позволило сэкономить 25% места при сохранении 95% первоначальной производительности системы и устранить проблемы нестабильности давления.
Заключение
Объем плоской сферы определяется по формуле V = (4/3)πa²b с экваториальным радиусом "a" и полярным радиусом "b". Сплющивание пропорционально уменьшает объем, но влияет на реакцию давления и характеристики потока в пневматических системах.
Вопросы и ответы об объеме плоской сферы
Какова формула объема плоской сферы?
Формула объема плоской сферы (продолговатого сфероида) - V = (4/3)πa²b, где "a" - экваториальный радиус (горизонтальный), а "b" - полярный радиус (вертикальный). Это отличается от формулы идеальной сферы V = (4/3)πr³.
Сколько объема теряется при сплющивании сферы?
Потеря объема равна коэффициенту сплющивания. Если полярный радиус составляет 70% от экваториального радиуса (b/a = 0,7), то объем становится равным 70% от первоначального объема сферы, что представляет собой уменьшение объема на 30%.
Где в пневматических системах используются плоские шары?
Плоские сферы используются в аккумуляторных камерах, системах амортизации и сосудах под давлением, где ограничения по высоте ограничивают стандартные сферические конструкции. К числу распространенных областей применения относятся интеграция в оборудование с ограниченным пространством и модернизация.
Как сплющивание влияет на производительность пневматики?
Сплющивание уменьшает объемную емкость, увеличивает чувствительность к давлению и создает турбулентность потока. В системах с сильно сплющенными аккумуляторами (b/a < 0,6) может наблюдаться нестабильность давления и снижение эффективности, требующее компенсации при проектировании.
Каков максимальный рекомендуемый коэффициент сплющивания?
Для пневматических систем следует поддерживать коэффициент сплющивания выше b/a = 0,6 для приемлемой работы. Коэффициенты ниже 0,4 обычно вызывают нестабильность системы и требуют значительных изменений в конструкции для поддержания адекватной работы.
-
Понять функции и назначение пневматических аккумуляторов в системах гидропривода. ↩
-
Узнайте математическое определение и геометрические свойства продолговатого сфероида. ↩
-
Смотрите официальное определение и требования к испытаниям для степени защиты от проникновения IP69K. ↩
-
Ознакомьтесь с принципами закона Бойля, который описывает зависимость между давлением и объемом газа. ↩
-
Изучите концепцию усталостной прочности и поведение материалов при циклических нагрузках. ↩




