Ingenjörer stöter på förvirring när de ska beräkna volymer för tillplattade sfäriska komponenter i stånglösa pneumatiska cylindersystem. Felaktiga volymberäkningar leder till felaktiga tryckberäkningar och systemfel.
En platt sfär (oblat sfäroid) har volymen V = (4/3)πa²b, där "a" är ekvatorialradien och "b" är polradien, vilket vanligen förekommer i pneumatisk ackumulator1 och stötdämpande tillämpningar.
Förra månaden hjälpte jag Andreas, en konstruktör från Tyskland, vars pneumatiska dämpningssystem inte fungerade eftersom han använde standardvolym för sfärer i stället för oblaterade sfäroider för sina tillplattade ackumulatorkammare.
Innehållsförteckning
- Vad är en platt sfär i pneumatiska applikationer?
- Hur beräknar man en platt sfärs volym?
- Var används platta sfärer i stånglösa cylindrar?
- Hur påverkar utplaning volym och prestanda?
Vad är en platt sfär i pneumatiska applikationer?
En platt sfär, tekniskt sett kallad en Oblat sfäroid2är en tredimensionell form som skapas när en sfär komprimeras längs en axel och som ofta används i pneumatiska ackumulatorer och dämpande konstruktioner.
En platt sfär är resultatet av att en perfekt sfär plattas ut längs sin vertikala axel, vilket skapar ett elliptiskt tvärsnitt med olika horisontella och vertikala radiemått.
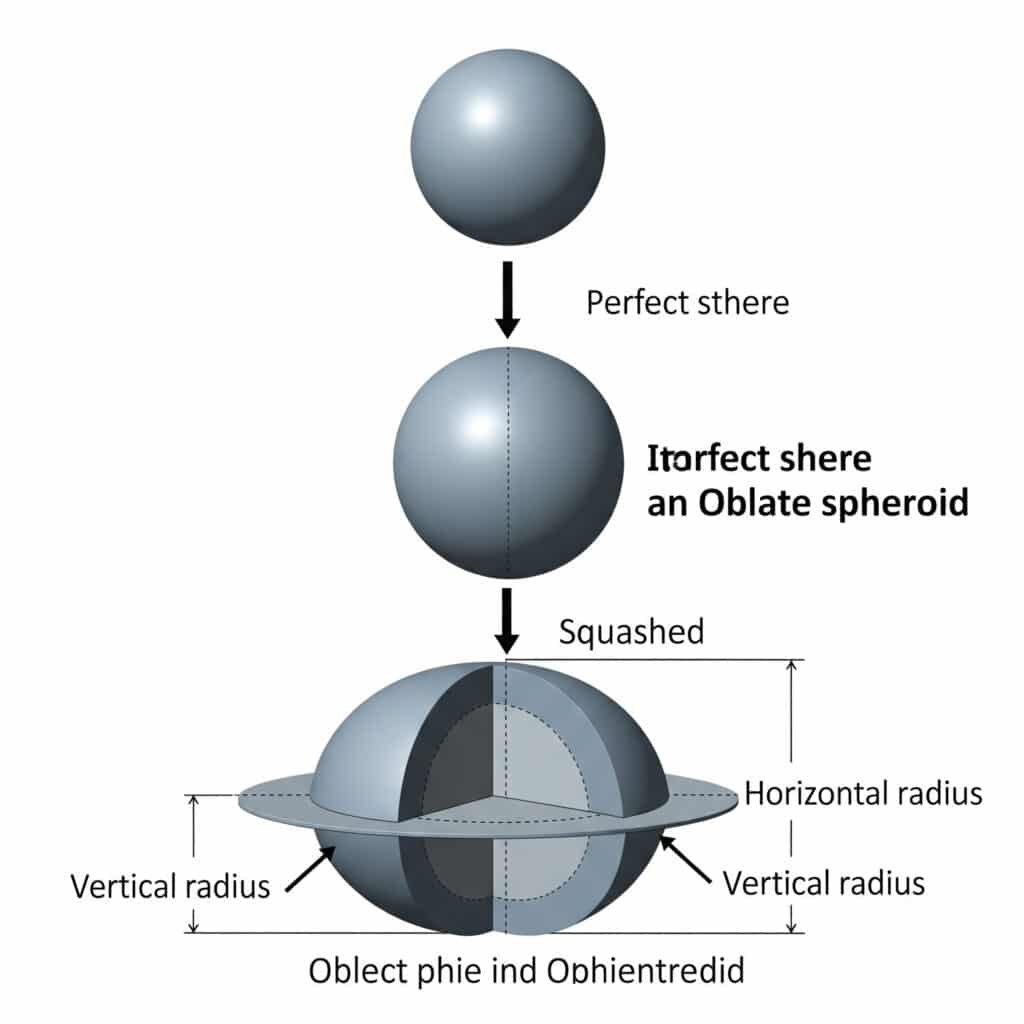
Geometrisk definition
Formegenskaper
- Oblat sfäroid: Teknisk geometrisk term
- Tillplattad sfär: Vanlig industriell beskrivning
- Elliptisk profil: Tvärsnittsvy
- Rotationssymmetri: Runt vertikal axel
Viktiga dimensioner
- Ekvatoriell radie (a): Horisontell radie (större)
- Polär radie (b): Vertikal radie (mindre)
- Utplanande förhållande: b/a < 1,0
- Aspect ratio: Förhållande mellan höjd och bredd
Platt sfär vs perfekt sfär
| Karaktäristisk | Perfekt sfär | Platt sfär |
|---|---|---|
| Form | Enhetlig radie | Komprimerad vertikalt |
| Formel för volym | (4/3)πr³ | (4/3)πa²b |
| Tvärsnitt | Cirkel | Ellips |
| Symmetri | Alla riktningar | Endast horisontellt |
Vanliga utjämningsrelationer
Ljusutplattning
- Förhållande: b/a = 0,8-0,9
- Tillämpningar: Lätta utrymmesbegränsningar
- Påverkan på volymen: 10-20% minskning
- Prestanda: Minimal effekt
Måttlig utplaning
- Förhållande: b/a = 0,6-0,8
- Tillämpningar: Standardutförande av ackumulatorer
- Påverkan på volymen: 20-40% minskning
- Prestanda: Märkbara tryckförändringar
Kraftig utplaning
- Förhållande: b/a = 0,3-0,6
- Tillämpningar: Kraftiga utrymmesbegränsningar
- Påverkan på volymen: 40-70% reducering
- Prestanda: Betydelsefulla designöverväganden
Pneumatiska tillämpningar
Ackumulatortankar
Jag stöter på platta sfärer i:
- Utrymmesbegränsade installationer: Begränsningar i höjdled
- Integrerad design: Inbyggda i maskinramar
- Anpassade applikationer: Specifika volymkrav
- Retrofit-projekt: Anpassning till befintliga utrymmen
Dämpningssystem
- Dämpning i slutet av slaget: Stånglösa cylinderapplikationer
- Stötdämpning: Hantering av effektbelastning
- Tryckreglering: Smidig driftskontroll
- Minskning av buller: Tystare drift av systemet
Överväganden om tillverkning
Produktionsmetoder
- Djupgående ritning: Plåtformning
- Hydroformning: Precisionsformningsprocess
- Maskinbearbetning: Anpassade komponenter för engångsbruk
- Gjutning: Produktion av stora volymer
Val av material
- Stål: Högtrycksapplikationer
- Aluminium: Viktkänsliga konstruktioner
- Rostfritt stål: Frätande miljöer
- Kompositmaterial: Specialiserade krav
Hur beräknar man en platt sfärs volym?
För att beräkna volymen på en platt sfär krävs formeln för en platt sfäroid med mätningar av både ekvatoriell och polär radie för en korrekt utformning av det pneumatiska systemet.
Använd formeln V = (4/3)πa²b där "a" är ekvatorialradien (horisontell) och "b" är polarradien (vertikal) för att beräkna en platt sfärs volym exakt.
Fördelning av volymformeln
Standardformel
V = (4/3)πa²b
- V: Volym i kubikenheter
- π: 3,14159 (matematisk konstant)
- a: Ekvatoriell radie (horisontell)
- b: Polär radie (vertikal)
- 4/3: Sfäroid volymkoefficient
Formelkomponenter
- Ekvatoriellt område: πa² (horisontellt tvärsnitt)
- Polar skalning: b-faktor (vertikal komprimering)
- Volymkoefficient: 4/3 (geometrisk konstant)
- Resultat enheter: Matchningsinmatning radie enheter kubik
Steg-för-steg-beräkning
Mätningsprocess
- Mät ekvatorialdiameter: Bredaste horisontella dimension
- Beräkna ekvatoriell radie: a = diameter ÷ 2
- Mät polär diameter: Vertikal höjddimension
- Beräkna polär radie: b = höjd ÷ 2
- Applicera formel: V = (4/3)πa²b
Exempel på beräkning
För en pneumatisk ackumulator:
- Ekvatoriell diameter: 100 mm → a = 50 mm
- Polär diameter: 60mm → b = 30mm
- Volym: V = (4/3)π(50)²(30)
- Resultat: V = (4/3)π(2500)(30) = 314.159 mm³
Exempel på volymberäkning
| Ekvatoriell radie | Polär radie | Utplanande förhållande | Volym | Jämförelse med sfär |
|---|---|---|---|---|
| 50 mm | 50 mm | 1.0 | 523.599 mm³ | 100% (perfekt sfär) |
| 50 mm | 40 mm | 0.8 | 418.879 mm³ | 80% |
| 50 mm | 30 mm | 0.6 | 314,159 mm³ | 60% |
| 50 mm | 20 mm | 0.4 | 209.440 mm³ | 40% |
Beräkningsverktyg
Manuell beräkning
- Vetenskaplig kalkylator: Med π-funktion
- Verifiering av formel: Dubbelkontrollera ingångar
- Enhetens konsistens: Behåll samma enheter hela tiden
- Precision: Beräkna till lämpliga decimaler
Digitala verktyg
- Programvara för ingenjörsarbete: CAD-volymberäkningar
- Kalkylatorer online: Oblat sfäroid verktyg
- Kalkylbladets formler: Automatiserade beräkningar
- Mobila appar: Verktyg för fältberäkning
Vanliga beräkningsfel
Misstag vid mätning
- Radie vs diameter: Använd fel dimension
- Förvirring kring axlarna: Blandning av horisontella/vertikala mätningar
- Inkonsekvens i enheten: mm vs tum blandning
- Precisionsförlust: Avrundning för tidigt
Fel i formeln
- Felaktig formel: Använda sfär istället för sfäroid
- Omkastning av parametrar: Byte av a- och b-värden
- Fel i koefficienten: Saknar 4/3-faktor
- π-tillnärmning: Använda 3.14 istället för 3.14159
Verifieringsmetoder
Tekniker för dubbelkontroll
- CAD-programvara: Volymberäkning av 3D-modell
- Vattenförskjutning: Fysisk volymmätning
- Flera beräkningar: Jämförelse av olika metoder
- Tillverkarens specifikationer: Publicerade volymuppgifter
Kontroll av skälighet
- Minskad volym: Bör vara mindre än perfekt sfär
- Utplanande korrelation: Mer utplaning = mindre volym
- Verifiering av enhet: Resultaten motsvarar den förväntade omfattningen
- Lämplighet för tillämpning: Volymen uppfyller systemkraven
När jag hjälpte Maria, en pneumatisk systemkonstruktör från Spanien, att beräkna ackumulatorvolymer för hennes stånglösa cylinderinstallation upptäckte vi att hennes ursprungliga beräkningar använde sfärformler istället för oblaterade sfäroidformler, vilket resulterade i en överskattning av 35%-volymen och otillräcklig systemprestanda.
Var används platta sfärer i stånglösa cylindrar?
Platta sfärer förekommer i olika stånglösa pneumatiska cylinderkomponenter där utrymmesbegränsningar kräver volymoptimering samtidigt som tryckkärlets funktionalitet bibehålls.
Platta sfärer används ofta i ackumulatorkammare, dämpningssystem och integrerade tryckkärl i stånglösa cylinderenheter där höjdbegränsningar begränsar sfäriska standardkonstruktioner.
Applikationer för ackumulatorer
Integrerade ackumulatorer
- Optimering av utrymme: Passar inom maskinens ramar
- Volymeffektivitet: Maximal förvaring på begränsad höjd
- Tryckstabilitet: Smidig drift under efterfrågetoppar
- Systemintegration: Inbyggd i cylinderns monteringsbas
Installationer för eftermontering
- Befintliga maskiner: Begränsningar för höjdskillnad
- Uppgraderingsprojekt: Lägga till ackumulering till äldre system
- Utrymmesbegränsningar: Arbete inom den ursprungliga designramen
- Förbättring av prestanda: Förbättrad systemrespons
Dämpningssystem
Dämpning vid slutet av slaget
Jag installerar platt sfärisk dämpning för:
- Magnetiska stånglösa cylindrar: Mjuk inbromsning
- Styrda stånglösa cylindrar: Minskning av påverkan
- Dubbelverkande stånglösa cylindrar: Dubbelriktad stötdämpning
- Höghastighetsapplikationer: Stötdämpning
Tryckreglering
- Utjämning av flöde: Eliminera tryckspikar
- Minskning av buller: Tystare drift
- Komponentskydd: Minskat slitage och mindre påfrestningar
- Systemets stabilitet: Konsekvent prestanda
Specialiserade komponenter
Tryckkärl
- Anpassade applikationer: Unika krav på utrymme
- Design med flera funktioner: Kombinerad förvaring och montering
- Modulära system: Stapelbara konfigurationer
- Tillträde för underhåll: Brukbara konstruktioner
Sensorkammare
- Övervakning av tryck: Integrerade mätsystem
- Flödesdetektering: Applikationer för hastighetsavkänning
- Systemdiagnostik: Övervakning av prestanda
- Säkerhetssystem: Integration av tryckavlastning
Överväganden om design
Utrymmesbegränsningar
| Tillämpning | Höjdgräns | Typisk utplaning | Påverkan på volym |
|---|---|---|---|
| Montering under golv | 50 mm | b/a = 0,3 | 70% reducering |
| Integration av maskiner | 100 mm | b/a = 0,6 | 40% minskning |
| Eftermonterade applikationer | 150 mm | b/a = 0,8 | 20% minskning |
| Standardmontering | 200 mm + | b/a = 0,9 | 10% minskning |
Krav på prestanda
- Tryckklassning: Upprätthålla strukturell integritet
- Volym kapacitet: Uppfylla systemets krav
- Flödesegenskaper: Lämplig dimensionering av inlopp/utlopp
- Tillträde för underhåll: Överväganden om servicevänlighet
Exempel på installation
Förpackningsmaskiner
- Tillämpning: Utrustning för höghastighetsfyllning
- Begränsning: 40 mm spel i höjdled
- Lösning: Kraftigt tillplattad ackumulator (b/a = 0,25)
- Resultat: 75% volymminskning, tillräcklig prestanda
Montering av fordon
- Tillämpning: Positioneringssystem för robotar
- Begränsning: Integration i robotbasen
- Lösning: Måttlig utplaning (b/a = 0,7)
- Resultat: 30% utrymmesbesparingar, bibehållen prestanda
Livsmedelsbearbetning
- Tillämpning: Sanitärt stånglöst cylindersystem
- Begränsning: Godkännande för tvättmiljö
- Lösning: Anpassad design för platt sfär
- Resultat: IP69K-klassning3 med optimerad volym
Specifikationer för tillverkning
Standardstorlekar
- Liten: 50 mm ekvatorial, olika polära dimensioner
- Medium: 100 mm ekvatoriellt, höjdvariationer
- Stor: 200 mm ekvatorial, anpassad polarstorlek
- Anpassad: Applikationsspecifika mått
Materialalternativ
- Kolstål: Standard tryckapplikationer
- Rostfritt stål: Frätande miljöer
- Aluminium: Viktkänsliga installationer
- Sammansatt: Specialiserade krav
Förra året arbetade jag med Thomas, en maskinbyggare från Schweiz, som behövde ackumulatorförvaring till sin kompakta förpackningslinje. Sfäriska standardackumulatorer passade inte in i höjdbegränsningen på 60 mm, så vi konstruerade platta sfäriska ackumulatorer med förhållandet b/a = 0,4, vilket gav 60% av den ursprungliga volymen samtidigt som alla utrymmesbegränsningar uppfylldes.
Hur påverkar utplaning volym och prestanda?
Plattning minskar volymkapaciteten avsevärt samtidigt som det påverkar tryckdynamiken, flödesegenskaperna och den övergripande systemprestandan i stånglösa pneumatiska applikationer.
Varje 10% ökning av utplaningen (minskning av b/a-förhållandet) minskar volymen med cirka 10% och påverkar tryckrespons, flödesmönster och systemeffektivitet i pneumatiska ackumulatortillämpningar.
Analys av volympåverkan
Relationer för volymminskning
Volymförhållande = (b/a) för avlånga sfäroider
- Linjärt förhållande: Volymen minskar proportionellt med utplaningen
- Förutsägbar effekt: Lätt att beräkna volymförändringar
- Flexibilitet i konstruktionen: Välj optimalt utjämningsförhållande
- Avvägningar mellan prestanda: Balans mellan utrymme och kapacitet
Kvantifierade volymförändringar
| Utplaningskvot (b/a) | Bevarande av volym | Volymförlust | Applikationens lämplighet |
|---|---|---|---|
| 0.9 | 90% | 10% | Utmärkt |
| 0.8 | 80% | 20% | Mycket bra |
| 0.7 | 70% | 30% | Bra |
| 0.6 | 60% | 40% | Rättvist |
| 0.5 | 50% | 50% | Dålig |
| 0.4 | 40% | 60% | Mycket dålig |
Tryck Prestanda Effekter
Karakteristik för tryckrespons
- Minskad volym: Snabbare tryckförändringar
- Högre känslighet: Mer lyhörd för flödesvariationer
- Ökad cykling: Mer frekventa laddnings-/urladdningscykler
- Instabilitet i systemet: Potentiella tryckoscillationer
Justeringar för tryckberäkning
P₁V₁ = P₂V₂ (Boyles lag4 gäller)
- Mindre volym: Högre tryck för samma luftmassa
- Tryckförändringar: Större variationer under drift
- Dimensionering av system: Kompensera med större kompressorkapacitet
- Säkerhetsmarginaler: Ökade krav på tryckklassning
Flödeskarakteristik
Förändringar i flödesmönster
- Ökad turbulens: Tillplattad form skapar flödesstörningar
- Tryckfall: Högre motstånd genom deformerade kammare
- Inlopps-/utloppseffekter: Hamnpositionering blir kritisk
- Flödeshastighet: Ökade hastigheter genom begränsade sektioner
Påverkan på flödeshastighet
- Minskad effektiv yta: Flödesbegränsningar utvecklas
- Tryckförluster: Energieffektiviteten minskar
- Svarstid: Långsammare fyllnings-/urladdningshastigheter
- Systemets prestanda: Minskad total effektivitet
Strukturella överväganden
Spänningsfördelning
- Koncentrerade påfrestningar: Högre belastningar på utplanade områden
- Materialets tjocklek: Kan kräva förstärkning
- Utmattningshållfasthet5: Potentiell minskad livscykel
- Säkerhetsfaktorer: Ökade konstruktionsmarginaler behövs
Tryckklassning Effekter
| Utplanande förhållande | Ökad stress | Rekommenderad säkerhetsfaktor | Materialets tjocklek |
|---|---|---|---|
| 0.9 | 10% | 1.5 | Standard |
| 0.8 | 25% | 1.8 | +10% |
| 0.7 | 45% | 2.0 | +20% |
| 0.6 | 70% | 2.5 | +35% |
Optimering av systemets prestanda
Ersättningsstrategier
- Ökad mängd ackumulatorer: Flera mindre enheter
- Drift vid högre tryck: Kompensera för volymförlust
- Förbättrad flödesdesign: Optimera konfigurationer för inlopp/utlopp
- Justering av systemet: Justera kontrollparametrar
Övervakning av prestanda
- Frekvens för tryckcykling: Övervaka systemets stabilitet
- Mätning av flödeshastighet: Verifiera tillräcklig kapacitet
- Temperaturpåverkan: Kontrollera om värmen är för hög
- Underhållsintervaller: Justeras baserat på resultat
Riktlinjer för design
Val av optimal utplaning
- b/a > 0,8: Minimal påverkan på prestanda
- b/a = 0,6-0,8: Godtagbar för de flesta tillämpningar
- b/a = 0,4-0,6: Kräver noggrann systemdesign
- b/a < 0,4: Rekommenderas i allmänhet inte
Applikationsspecifika rekommendationer
- Högfrekvent cykling: Minimera utplaning (b/a > 0,7)
- Rymdkritiska installationer: Acceptera avvägningar mellan prestanda
- Säkerhetskritiska system: Konservativa utplaningskvoter
- Kostnadskänsliga projekt: Balansera prestanda mot utrymmesbesparingar
Data om prestanda i den verkliga världen
Resultat av fallstudie
När jag analyserade prestandadata från 50 installationer med olika utjämningsförhållanden:
- 10% utplaning: Försumbar påverkan på prestanda
- 30% utplaning: 15% ökning av cykelfrekvensen
- 50% utplaning: 40% minskning av den effektiva kapaciteten
- 70% utplaning: Systeminstabilitet i 60% av fallen
Framgång med optimering
För Elena, en systemintegratör från Italien, optimerade vi konstruktionen av hennes stånglösa cylinderackumulator genom att begränsa utplaningen till b/a = 0,75, vilket gav 25% utrymmesbesparingar samtidigt som 95% av systemets ursprungliga prestanda bibehölls och problem med tryckinstabilitet eliminerades.
Slutsats
Volymen hos en platt sfär beräknas med formeln V = (4/3)πa²b med ekvatoriell radie "a" och polär radie "b". Plattning minskar volymen proportionellt men påverkar tryckrespons och flödesegenskaper i pneumatiska applikationer.
Vanliga frågor om platt sfärvolym
Vad är formeln för en platt sfärs volym?
Den platta sfärens (oblat sfäroidens) volymformel är V = (4/3)πa²b, där "a" är ekvatorialradien (horisontell) och "b" är polradien (vertikal). Detta skiljer sig från en perfekt sfärs formel V = (4/3)πr³.
Hur mycket volym går förlorad när man plattar till en sfär?
Volymförlusten är lika med utplaningsförhållandet. Om polradien är 70% av ekvatorradien (b/a = 0,7) blir volymen 70% av den ursprungliga sfärvolymen, vilket motsvarar en volymminskning på 30%.
Var används platta sfärer i pneumatiska system?
Platta sfärer används i ackumulatorkammare, dämpningssystem och tryckkärl där höjdbegränsningar begränsar sfäriska standardkonstruktioner. Vanliga tillämpningar är utrymmesbegränsade maskinintegreringar och eftermonterade installationer.
Hur påverkar utplaning pneumatisk prestanda?
Avplaning minskar volymkapaciteten, ökar tryckkänsligheten och skapar flödesturbulens. System med kraftigt tillplattade ackumulatorer (b/a < 0,6) kan drabbas av tryckinstabilitet och minskad effektivitet, vilket kräver kompensation i konstruktionen.
Vad är det högsta rekommenderade utjämningsförhållandet?
För pneumatiska tillämpningar bör utjämningskvoter över b/a = 0,6 bibehållas för acceptabel prestanda. Förhållanden under 0,4 orsakar i allmänhet systeminstabilitet och kräver betydande konstruktionsändringar för att upprätthålla tillfredsställande drift.
-
Förstå funktionen och syftet med pneumatiska ackumulatorer i vätskekraftsystem. ↩
-
Lär dig den matematiska definitionen och de geometriska egenskaperna hos en oblat sfäroid. ↩
-
Se den officiella definitionen och testkraven för IP69K-klassningen av inträngningsskydd. ↩
-
Gå igenom principerna för Boyles lag, som beskriver förhållandet mellan tryck och volym i en gas. ↩
-
Utforska begreppet utmattningshållfasthet och hur material beter sig under cyklisk belastning. ↩




