Інженери стикаються з труднощами при обчисленні об'ємів сплющених сферичних компонентів у безштокових пневмоциліндрових системах. Неправильні розрахунки об'єму призводять до прорахунків тиску та відмов системи.
Плоска сфера (косий сфероїд) має об'єм V = (4/3)πa²b, де "a" - екваторіальний радіус, а "b" - полярний радіус, що зазвичай зустрічається у пневматичний акумулятор1 та амортизаційних застосувань.
Минулого місяця я допоміг Андреасу, інженеру-конструктору з Німеччини, чия пневматична система амортизації вийшла з ладу через те, що він використовував стандартний об'єм сфери замість розрахунків косокутного сфероїда для своїх сплющених камер акумулятора.
Зміст
- Що таке плоска сфера в пневматичних системах?
- Як обчислити об'єм плоскої сфери?
- Де використовуються плоскі сфери в безштокових циліндрах?
- Як сплющення впливає на гучність і продуктивність?
Що таке плоска сфера в пневматичних системах?
Плоска сфера, яка технічно називається косий сфероїд2тривимірна форма, що утворюється при стисненні сфери вздовж однієї осі, зазвичай використовується в конструкціях пневматичних акумуляторів і амортизаторів.
Плоска сфера утворюється в результаті сплющення ідеальної сфери вздовж її вертикальної осі, створюючи еліптичний переріз з різними вимірами горизонтального та вертикального радіусів.
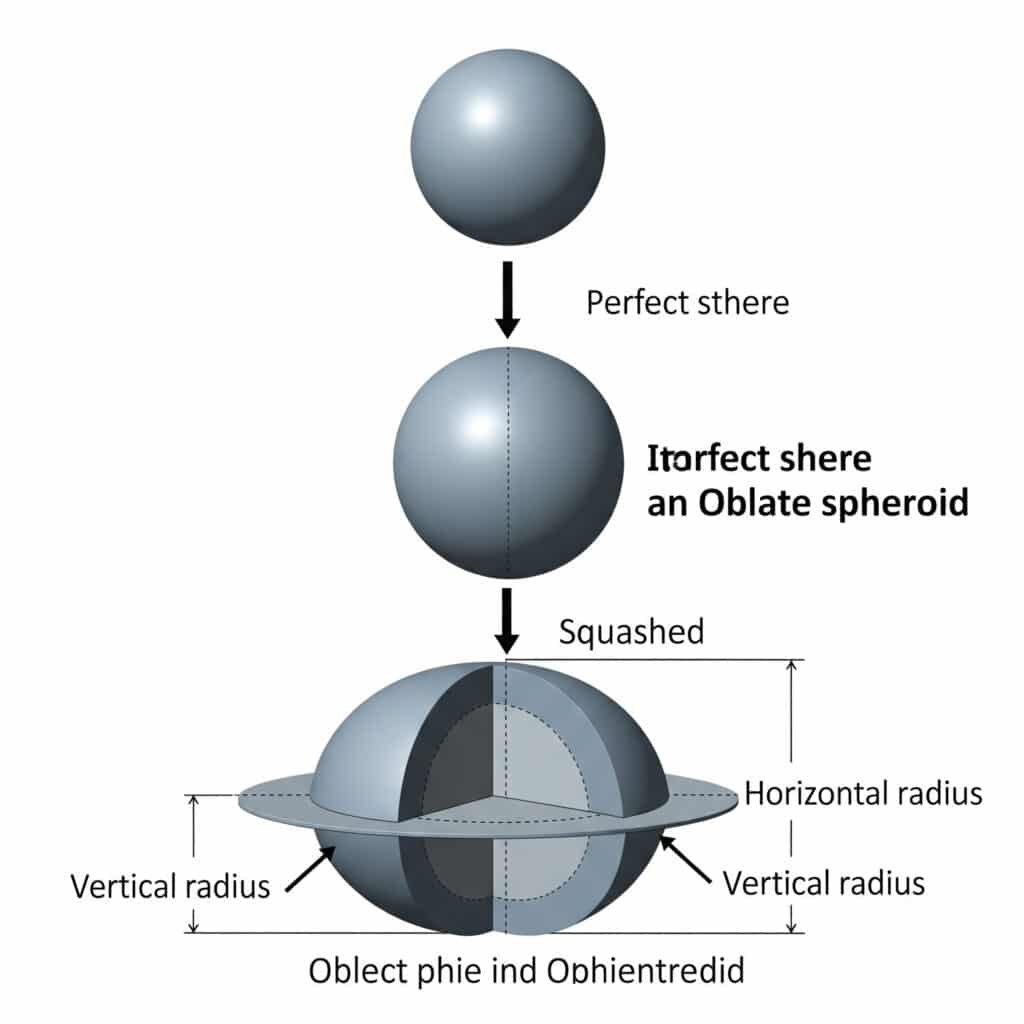
Геометричне визначення
Характеристики форми
- Косий сфероїд: Технічний геометричний термін
- Плоска сфера: Загальний промисловий опис
- Еліптичний профіль: Поперечний переріз : Поперечний переріз
- Симетрія обертання: Навколо вертикальної осі
Ключові виміри
- Екваторіальний радіус (a): Горизонтальний радіус (більший)
- Полярний радіус (b): Вертикальний радіус (менший)
- Коефіцієнт сплющення: b/a < 1.0
- Співвідношення сторін: Відношення висоти до ширини
Плоска сфера vs Ідеальна сфера
| Характеристика | Ідеальна сфера | Плоска сфера |
|---|---|---|
| Форма | Рівномірний радіус | Стиснутий по вертикалі |
| Формула об'єму | (4/3)πr³ | (4/3)πa²b |
| Поперечний переріз | Коло | Еліпс |
| Симетрія | Всі напрямки | Тільки в горизонтальному положенні |
Загальні коефіцієнти вирівнювання
Легке вирівнювання
- Співвідношення: b/a = 0.8-0.9
- Додатки: Невеликі просторові обмеження
- Вплив обсягу: 10-20% зменшення
- Продуктивність: Мінімальний ефект
Помірне вирівнювання
- Співвідношення: b/a = 0.6-0.8
- Додатки: Стандартні конструкції акумуляторів
- Вплив обсягу: скорочення 20-40%
- Продуктивність: Помітні зміни тиску
Важке сплющення
- Співвідношення: b/a = 0.3-0.6
- Додатки: Суворі обмеження простору
- Вплив обсягу: 40-70% зменшення
- Продуктивність: Важливі міркування щодо дизайну
Пневматичні застосування
Акумуляторні камери
Я зустрічаю плоскі сфери:
- Інсталяції з обмеженим простором: Обмеження по висоті
- Інтегровані конструкції: Вбудовані в рами машин
- Користувацькі програми: Специфічні вимоги до обсягу
- Проекти модернізації: Пристосування існуючих просторів
Системи амортизації
- Демпферування в кінці ходу: Застосування безштокових циліндрів
- Поглинання ударів: Управління ударним навантаженням
- Регулювання тиску: Плавне керування роботою
- Зниження рівня шуму: Тихіша робота системи : Тихіша робота системи
Виробничі міркування
Методи виробництва
- Глибокий малюнок: Обробка листового металу
- Гідроформування: Прецизійний процес формування
- Механічна обробка: Індивідуальні компоненти на замовлення
- Кастинг: Великосерійне виробництво
Вибір матеріалу
- Сталь: Застосування під високим тиском
- Алюміній: Конструкції, чутливі до ваги
- Нержавіюча сталь: Корозійні середовища : Корозійні середовища
- Композитні матеріали: Спеціалізовані вимоги
Як обчислити об'єм плоскої сфери?
Для точного розрахунку об'єму плоскої сфери потрібна формула косого сфероїда з використанням як екваторіального, так і полярного радіусів для точного проектування пневматичної системи.
Використовуйте формулу V = (4/3)πa²b, де "a" - екваторіальний радіус (по горизонталі), а "b" - полярний радіус (по вертикалі), щоб точно обчислити об'єм пласкої сфери.
Розбивка за формулою обсягу
Стандартна формула
V = (4/3)πa²b
- V: Об'єм в кубічних одиницях
- π: 3.14159 (математична константа)
- a: Екваторіальний радіус (по горизонталі)
- b: Полярний радіус (вертикальний)
- 4/3: Коефіцієнт об'єму сфероїда
Компоненти формули
- Екваторіальна зона: πa² (горизонтальний переріз)
- Полярне масштабування: коефіцієнт b (вертикальне стиснення)
- Об'ємний коефіцієнт: 4/3 (геометрична константа)
- Одиниці виміру результату: Зіставити вхідні одиниці радіусу в кубічних одиницях
Покроковий розрахунок
Процес вимірювання
- Виміряйте екваторіальний діаметр: Найширший горизонтальний розмір
- Обчислити екваторіальний радіус: a = діаметр ÷ 2
- Виміряйте полярний діаметр: Вертикальний розмір висоти : Вертикальний розмір висоти
- Розрахувати полярний радіус: b = height ÷ 2
- Застосувати формулу: V = (4/3)πa²b
Приклад розрахунку
Для пневматичного акумулятора:
- Екваторіальний діаметр: 100мм → a = 50мм
- Полярний діаметр: 60мм → b = 30мм
- Обсяг: V = (4/3)π(50)²(30)
- Результат: V = (4/3)π(2500)(30) = 314,159 мм³.
Приклади розрахунку об'єму
| Екваторіальний радіус | Полярний радіус | Коефіцієнт сплющення | Обсяг | Порівняння зі сферою |
|---|---|---|---|---|
| 50 мм | 50 мм | 1.0 | 523 599 мм³ | 100% (ідеальна сфера) |
| 50 мм | 40 мм | 0.8 | 418 879 мм³ | 80% |
| 50 мм | 30 мм | 0.6 | 314 159 мм³ | 60% |
| 50 мм | 20 мм | 0.4 | 209 440 мм³ | 40% |
Інструменти розрахунку
Розрахунок вручну
- Науковий калькулятор: З функцією π
- Перевірка формули: Перевірте вхідні дані
- Узгодженість одиниць виміру: Підтримувати однакові одиниці протягом усього часу
- Точність: Обчислити з точністю до десяткових знаків
Цифрові інструменти
- Інженерне програмне забезпечення: Об'ємні розрахунки CAD
- Онлайн-калькулятори: Косокутні сфероїдні інструменти
- Формули електронних таблиць: Автоматизовані розрахунки
- Мобільні додатки: Інструменти для розрахунку поля
Поширені помилки обчислень
Помилки вимірювання
- Радіус проти діаметра: Використання неправильного розміру
- Плутанина осей: Змішування горизонтальних/вертикальних вимірювань
- Неузгодженість одиниць вимірузмішування мм та дюймів
- Втрата точності: Занадто раннє округлення
Помилки у формулах
- Неправильна формула: Використання сфери замість сфероїда
- Зміна параметрів: Обмін місцями значень a та b
- Помилки в коефіцієнтах: Відсутній коефіцієнт 4/3
- π-апроксимація: Використання 3.14 замість 3.14159
Методи перевірки
Методи перехресної перевірки
- Програмне забезпечення для САПР: Розрахунок об'єму 3D моделі
- Витіснення води: Вимірювання фізичного об'єму
- Багаторазові розрахунки: Порівняння різних методів
- Технічні характеристики виробника: Опубліковані дані про обсяги
Перевірка обґрунтованості
- Зменшення об'єму: Повинна бути меншою за ідеальну сферу
- Кореляція згладжування: Більше сплющення = менше об'єму
- Перевірка пристрою: Результати відповідають очікуваній величині
- Придатність для застосування: Обсяг відповідає системним вимогам
Коли я допомагав Марії, дизайнеру пневматичних систем з Іспанії, розрахувати об'єми акумуляторів для її безштокової установки, ми виявили, що в її оригінальних розрахунках використовувалися формули сфери замість косокутного сфероїда, що призвело до завищення об'єму 35% і неадекватної продуктивності системи.
Де використовуються плоскі сфери в безштокових циліндрах?
Плоскі сфери з'являються в різних компонентах безштокових пневматичних циліндрів, де обмежений простір вимагає оптимізації об'єму при збереженні функціональності посудини під тиском.
Плоскі сфери зазвичай використовуються в акумуляторних камерах, амортизаційних системах та інтегрованих посудинах під тиском у складі безштокових циліндрів, де обмеження по висоті обмежують стандартні сферичні конструкції.
Застосування акумуляторів
Вбудовані акумулятори
- Оптимізація простору: Вписується в рами машин
- Об'ємна ефективність: Максимальне зберігання на обмеженій висоті
- Стабільність тиску: Безперебійна робота під час пікових навантажень
- Системна інтеграція: Вбудовані в циліндричні монтажні основи
Модернізація установок
- Існуюча техніка: Обмеження по висоті зазору
- Проекти модернізації: Додавання накопичення до старих систем
- Обмеженість простору: Робота в межах оригінальної проектної оболонки
- Підвищення продуктивності: Покращена реакція системи
Системи амортизації
Демпфірування в кінці ходу
Я встановлюю плоскі сферичні подушки для:
- Магнітні безштокові циліндри: Плавне уповільнення
- Керовані безштокові циліндри: Зменшення впливу
- Безштокові циліндри подвійної дії: Двонаправлена амортизація
- Високошвидкісні програми: Поглинання ударів
Регулювання тиску
- Згладжування потоку: Усунення стрибків тиску
- Зниження рівня шуму: Тихіша робота
- Захист компонентів: Зменшення зносу та стресу
- Стабільність системи: Послідовна продуктивність
Спеціалізовані компоненти
Посудини під тиском
- Користувацькі програми: Унікальні вимоги до простору
- Багатофункціональні конструкції: Комбіноване зберігання та монтаж
- Модульні системи: Стекові конфігурації : Стекові конфігурації
- Доступ до технічного обслуговування: Придатні до експлуатації конструкції
Сенсорні камери
- Контроль тиску: Інтегровані вимірювальні системи
- Виявлення потоку: Застосування датчиків швидкості
- Діагностика системи: Моніторинг ефективності
- Системи безпеки: Інтеграція системи скидання тиску
Дизайнерські міркування
Обмеженість простору
| Заявка | Обмеження по висоті | Типове вирівнювання | Об'ємний вплив |
|---|---|---|---|
| Монтаж під підлогою | 50 мм | b/a = 0.3 | 70% скорочення |
| Інтеграція машин | 100 мм | b/a = 0.6 | 40% скорочення |
| Застосування для модернізації | 150 мм | b/a = 0.8 | Скорочення 20% |
| Стандартне кріплення | 200мм+ | b/a = 0.9 | Скорочення 10% |
Вимоги до продуктивності
- Номінальний тиск: Підтримуйте структурну цілісність
- Об'ємна потужність: Задоволення системного попиту
- Витратні характеристики: Відповідний розмір вхідного/вихідного отвору
- Доступ до технічного обслуговування: Міркування щодо експлуатаційної придатності
Приклади встановлення
Пакувальне обладнання
- Заявка: Високошвидкісне фасувальне обладнання
- Обмеження: Зазор по висоті 40 мм
- Рішення: Сильно сплющений акумулятор (b/a = 0,25)
- Результат75% : Зменшення об'єму, достатня продуктивність
Складання автомобілів
- Заявка: Роботизована система позиціонування
- Обмеження: Інтеграція в робототехнічну базу
- Рішення: Помірне вирівнювання : Помірне вирівнювання (b/a = 0.7)
- Результат: 30%: економія місця, збережена продуктивність
Харчова промисловість
- Заявка: Санітарна безштокова циліндрична система
- Обмеження: Очищення середовища для промивання
- Рішення: Індивідуальний дизайн плоскої сфери
- Результат: Ступінь захисту IP69K3 з оптимізованим об'ємом
Виробничі характеристики
Стандартні розміри
- Малий: 50 мм екваторіальний, різні полярні розміри
- Середній: 100 мм екваторіальна, варіації висоти
- Великий200 мм екваторіальний, індивідуальний полярний розмір
- Нестандартний: Розміри для конкретних застосувань
Варіанти матеріалів
- Вуглецева сталь: Стандартні застосування під тиском
- Нержавіюча сталь: Корозійні середовища : Корозійні середовища
- Алюміній: Інсталяції, чутливі до ваги
- Композит: Спеціалізовані вимоги
Минулого року я працював з Томасом, машинобудівником зі Швейцарії, якому потрібен був акумулятор для його компактної пакувальної лінії. Стандартні сферичні акумулятори не вписувалися в 60-міліметрове обмеження по висоті, тому ми розробили плоскі сферичні акумулятори зі співвідношенням b/a = 0,4, що дозволило отримати 60% від початкового об'єму при дотриманні всіх обмежень по простору.
Як сплющення впливає на гучність і продуктивність?
Сплющення значно зменшує об'ємну ємність, впливаючи на динаміку тиску, характеристики потоку та загальну продуктивність системи в безштокових пневматичних системах.
Кожне збільшення сплющення на 10% (зменшення співвідношення b/a) зменшує об'єм приблизно на 10% і впливає на реакцію на тиск, схему потоку та ефективність системи в пневматичних акумуляторах.
Аналіз впливу обсягу
Співвідношення зменшення об'єму
Відношення об'ємів = (b/a) для косих сфероїдів
- Лінійна залежність: Об'єм пропорційно зменшується зі сплющенням
- Передбачуваний вплив: Легко розрахувати зміну об'єму
- Гнучкість дизайну: Виберіть оптимальний коефіцієнт розплющування
- Компроміси щодо продуктивності: Баланс між простором і потужністю
Кількісні зміни обсягів
| Коефіцієнт сплющення (б/п) | Збереження об'єму | Втрата гучності | Придатність для застосування |
|---|---|---|---|
| 0.9 | 90% | 10% | Чудово. |
| 0.8 | 80% | 20% | Дуже добре. |
| 0.7 | 70% | 30% | Добре. |
| 0.6 | 60% | 40% | Справедливо |
| 0.5 | 50% | 50% | Бідолаха. |
| 0.4 | 40% | 60% | Дуже погано |
Вплив продуктивності під тиском
Характеристики реакції на тиск
- Зменшений об'єм: Швидша зміна тиску
- Підвищена чутливість: Швидше реагує на зміни потоку
- Збільшення кількості велосипедних прогулянок: Частіші цикли заряду/розряду
- Нестабільність системи: Потенційні коливання тиску : Потенційні коливання тиску
Налаштування розрахунку тиску
P₁V₁ = P₂V₂ (Закон Бойля4 застосовується)
- Менший об'єм: Вищий тиск для тієї ж маси повітря
- Перепади тиску: Більші коливання під час роботи
- Розмір системи: Компенсація за рахунок більшої продуктивності компресора
- Запас міцності: Підвищені вимоги до номінального тиску
Характеристики потоку
Зміни в структурі потоку
- Збільшення турбулентності: Сплющена форма створює збурення потоку
- Падіння тиску: Підвищений опір завдяки деформованим камерам
- Ефекти на вході/виході: Позиціонування порту стає критично важливим
- Швидкість потоку: Збільшення швидкості на ділянках з обмеженим доступом
Вплив на швидкість потоку
- Зменшення ефективної площі: Розвиваються обмеження потоку
- Втрати тиску: Енергоефективність знижується
- Час реагування: Повільніша швидкість заповнення/вивантаження
- Продуктивність системи: Загальне зниження ефективності
Структурні міркування
Розподіл навантаження
- Концентровані навантаження: Вищі навантаження на сплющених ділянках
- Товщина матеріалу: Може знадобитися посилення
- Стійкість до втоми5: Зменшення потенціалу життєвого циклу
- Фактори безпеки: Необхідно збільшити проектні запаси
Вплив номінального тиску
| Коефіцієнт сплющення | Збільшення стресу | Рекомендований коефіцієнт безпеки | Товщина матеріалу |
|---|---|---|---|
| 0.9 | 10% | 1.5 | Стандартний |
| 0.8 | 25% | 1.8 | +10% |
| 0.7 | 45% | 2.0 | +20% |
| 0.6 | 70% | 2.5 | +35% |
Оптимізація продуктивності системи
Стратегії компенсації
- Збільшена кількість акумуляторів: Кілька менших одиниць
- Робота під високим тиском: Компенсація втрати об'єму
- Покращений дизайн потоку: Оптимізація конфігурації входу/виходу
- Налаштування системи: Налаштування параметрів керування
Моніторинг ефективності
- Частота циклів тиску: Моніторинг стабільності системи
- Вимірювання швидкості потоку: Переконайтеся в наявності достатньої потужності
- Температурні ефекти: Перевірте, чи немає надмірного нагрівання
- Інтервали технічного обслуговування: Налаштуйте на основі продуктивності
Керівництво з проектування
Оптимальний вибір вирівнювання
- b/a > 0.8: Мінімальний вплив на продуктивність
- b/a = 0,6-0,8: Прийнятно для більшості застосувань
- b/a = 0,4-0,6: Потребує ретельного проектування системи
- b/a < 0.4: Як правило, не рекомендується
Рекомендації для конкретних застосувань
- Високочастотна циклічність: Мінімізація сплющення (b/a > 0,7)
- Критично важливі для простору інсталяції: Прийняти компроміси щодо продуктивності
- Критично важливі для безпеки системи: Консервативні коефіцієнти вирівнювання : Консервативні коефіцієнти вирівнювання
- Проекти, чутливі до витрат: Збалансувати продуктивність та економію місця
Реальні дані про продуктивність
Результати тематичного дослідження
Коли я проаналізував дані про продуктивність 50 установок з різним коефіцієнтом сплющення:
- 10% плющення: Незначний вплив на продуктивність
- 30% плющення: 15% збільшення частоти циклів
- 50% плющення: 40% зменшення ефективної потужності
- 70% плющення: Нестабільність системи в 60% випадків
Успіх оптимізації
Для компанії Elena, системного інтегратора з Італії, ми оптимізували конструкцію безштокового циліндричного акумулятора, обмеживши сплющення до b/a = 0,75, що дозволило заощадити 25% місця, зберігши при цьому 95% початкової продуктивності системи та усунувши проблеми з нестабільністю тиску.
Висновок
Об'єм плоскої сфери визначається за формулою V = (4/3)πa²b з екваторіальним радіусом 'a' і полярним радіусом 'b'. Сплющення пропорційно зменшує об'єм, але впливає на характеристики тиску та витрати в пневматичних системах.
Поширені запитання про об'єм плоскої сфери
Яка формула для об'єму плоскої сфери?
Формула об'єму плоскої сфери (косокутного сфероїда) має вигляд V = (4/3)πa²b, де "a" - екваторіальний радіус (по горизонталі), а "b" - полярний радіус (по вертикалі). Це відрізняється від формули об'єму ідеальної сфери V = (4/3)πr³.
Скільки об'єму втрачається при сплющуванні сфери?
Втрата об'єму дорівнює коефіцієнту сплющення. Якщо полярний радіус становить 70% екваторіального радіуса (b/a = 0.7), то об'єм стає 70% початкового об'єму сфери, що означає зменшення об'єму на 30%.
Де використовуються плоскі сфери в пневматичних системах?
Плоскі сфери використовуються в акумуляторних камерах, амортизаційних системах і посудинах під тиском, де висота обмежує стандартні сферичні конструкції. Поширеними сферами застосування є інтеграція обладнання в умовах обмеженого простору та модернізація установок.
Як сплющення впливає на пневматичні характеристики?
Сплющення зменшує об'ємну ємність, підвищує чутливість до тиску і створює турбулентність потоку. Системи з сильно сплющеними акумуляторами (b/a < 0,6) можуть мати нестабільність тиску і знижену ефективність, що вимагає компенсації при проектуванні.
Який максимальний рекомендований коефіцієнт сплющення?
Для пневматичних систем слід підтримувати коефіцієнт сплющення вище b/a = 0,6 для забезпечення прийнятної продуктивності. Співвідношення нижче 0,4, як правило, призводить до нестабільності системи і вимагає значних модифікацій конструкції для підтримання належної роботи.
-
Розуміти функції та призначення пневматичних акумуляторів у рідинних енергетичних системах. ↩
-
Вивчіть математичне означення та геометричні властивості косокутного сфероїда. ↩
-
Дивіться офіційне визначення та вимоги до випробувань для класу захисту від проникнення IP69K. ↩
-
Повторити принципи закону Бойля, який описує взаємозв'язок між тиском і об'ємом газу. ↩
-
Вивчіть концепцію опору втомі та поведінку матеріалів під час циклічних навантажень. ↩




