
هل تعاني من عدم اتساق سرعات الأسطوانة الهوائية أو تأثيرات نهاية الشوط غير المتوقعة؟ غالبًا ما تنبع هذه المشاكل الشائعة من سوء فهم حركية المكبس. يركز العديد من المهندسين فقط على متطلبات القوة بينما يتجاهلون معلمات الحركة الحرجة التي تحدد أداء النظام.
حركية المكبس1 تؤثر بشكل مباشر على أداء النظام الهوائي من خلال علاقات الضغط والسرعة وحدود التسارع ومتطلبات التوسيد. يسمح فهم هذه المبادئ للمهندسين بتحديد حجم المكونات بشكل صحيح، والتنبؤ بملامح الحركة الفعلية، ومنع الأعطال المبكرة في الأسطوانات بدون قضيب وغيرها من المشغلات الهوائية.
خلال عملي لأكثر من 15 عامًا في شركة Bepto في مجال الأنظمة الهوائية، رأيت حالات لا حصر لها ساعد فيها فهم هذه المبادئ الأساسية العملاء على حل مشكلات الأداء المستمرة وإطالة عمر المعدات بمقدار 3-5 مرات.
جدول المحتويات
- ما هو الضغط الذي تحتاجه فعلياً للحركة بسرعة ثابتة؟
- كيف تحسب أقصى تسارع ممكن في الأسطوانات الهوائية؟
- ما أهمية وقت التوسيد وكيف يتم حسابه؟
- الخاتمة
- الأسئلة الشائعة حول حركية المكبس في الأنظمة الهوائية
ما هو الضغط الذي تحتاجه فعلياً للحركة بسرعة ثابتة؟
يطبق العديد من المهندسين ببساطة أقصى ضغط متاح على أنظمتهم الهوائية، ولكن هذا النهج غير فعال ويمكن أن يؤدي إلى حركة متشنجة وتآكل مفرط وإهدار للطاقة.
يتم حساب الضغط المطلوب لحركة ثابتة السرعة في أسطوانة تعمل بالهواء المضغوط باستخدام P = (F + Fr)/A، حيث P هو الضغط، وF هي قوة الحمل الخارجي، وF هي قوة الحمل الخارجي، وF هي مقاومة الاحتكاك، وA هي مساحة المكبس. يضمن هذا الحساب التشغيل السلس والفعال دون ضغط مفرط يهدر الطاقة ويسرع من تآكل المكونات.
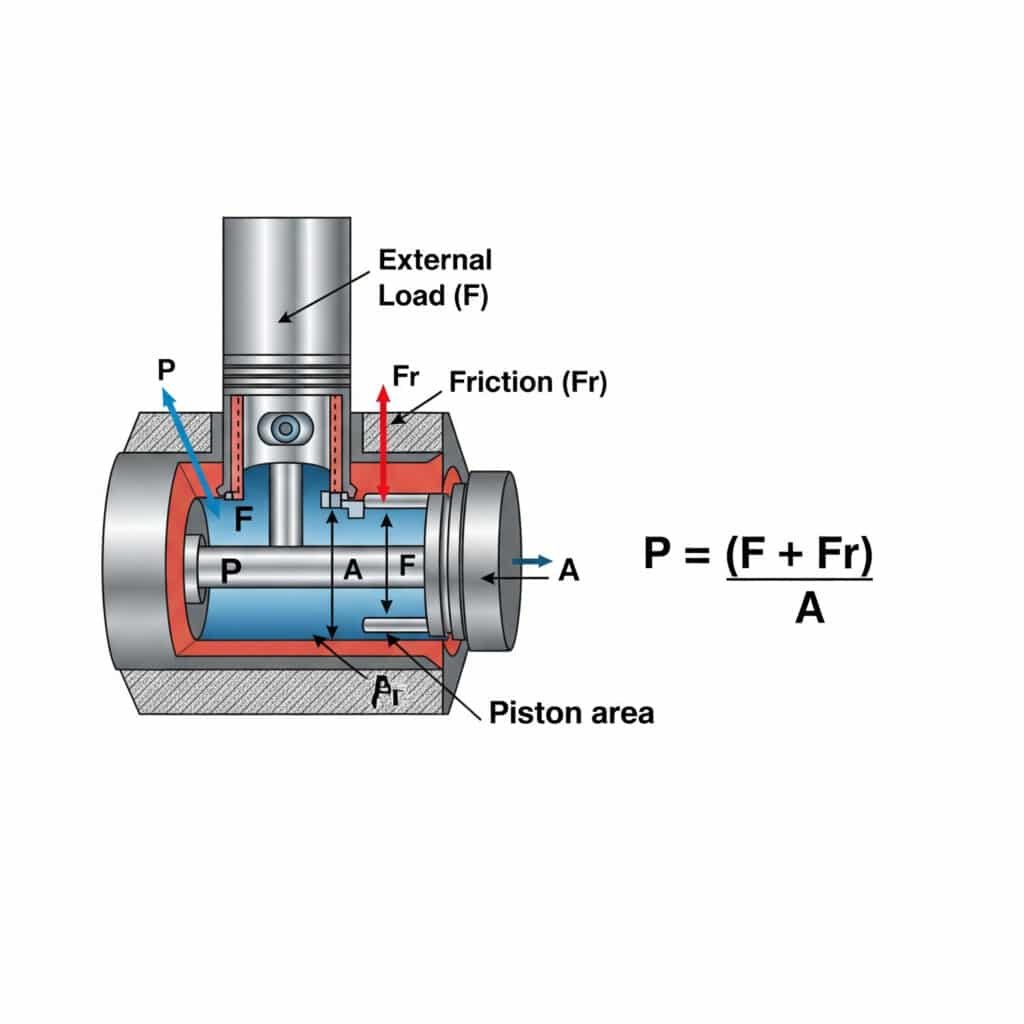
إن فهم متطلبات الضغط للحركة بسرعة ثابتة له آثار عملية على تصميم النظام وتشغيله. دعوني أقسم هذا إلى رؤى قابلة للتنفيذ.
العوامل المؤثرة على متطلبات الضغط للسرعة الثابتة
يعتمد الضغط اللازم للحفاظ على سرعة ثابتة على عدة عوامل:
| العامل | التأثير على متطلبات الضغط | اعتبارات عملية |
|---|---|---|
| الحمولة الخارجية | علاقة خطية مباشرة | يختلف باختلاف التوجه والقوى الخارجية |
| الاحتكاك | يضيف إلى الضغط المطلوب | التغييرات مع تآكل مانع التسرب والتشحيم |
| منطقة المكبس | تناسب عكسي | تجويف أكبر = متطلبات ضغط أقل |
| قيود إمدادات الهواء | انخفاض الضغط في الخطوط/الصمامات | حجم المكونات للحد من انخفاض الضغط إلى أدنى حد ممكن |
| الضغط الخلفي | يعارض الاقتراح | النظر في سعة تدفق العادم |
حساب الضغط الأدنى للحركة المستقرة
لتحديد الحد الأدنى من الضغط اللازم للحركة المستقرة:
- احسب القوة المطلوبة للتغلب على الحمل الخارجي
- أضف قوة الاحتكاك (عادةً 3-20% من القوة القصوى)
- القسمة على مساحة المكبس الفعالة
- إضافة عامل ثبات (عادةً 10-30%)
على سبيل المثال، في أسطوانة بدون قضيب ذات تجويف 40 مم مع حمولة 10 كجم واحتكاك 15%:
| المعلمة | الحساب | النتيجة |
|---|---|---|
| قوة التحميل | 10 كجم × 9.81 م/ث² | 98.1N |
| قوة الاحتكاك | 15% من القوة القصوى عند 6 بار | ~45N |
| إجمالي القوة | 98.1 نيوتن + 45 نيوتن | 143.1N |
| منطقة المكبس | π × (0.02م) ² | 0.00126m² |
| الحد الأدنى للضغط | 143.1 نيوتن ÷ 0.00126 م² | 113,571 باسكال (1.14 بار) |
| مع عامل الثبات 20% | 1.14 بار × 1.2 | 1.37 بار |
تطبيق واقعي: توفير الطاقة من خلال تحسين الضغط
عملت العام الماضي مع روبرت، وهو مهندس إنتاج في مصنع لتصنيع الأثاث في ميشيغان. كان خط التجميع الآلي الخاص به يستخدم أسطوانات بدون قضبان تعمل بضغط إمداد 6 بار كامل، بغض النظر عن الحمولة.
بعد تحليل تطبيقه، قررنا أن معظم الحركات لا تتطلب سوى 2.5-3 بار للتشغيل المستقر. من خلال تركيب منظمات الضغط النسبيخفضنا استهلاك الهواء بمقدار 401 تيرابايت 3 تيرابايت مع الحفاظ على نفس وقت الدورة. وقد وفر ذلك ما يقرب من $12,000T سنويًا من تكاليف الطاقة مع تقليل تآكل مانع التسرب وإطالة فترات الصيانة.
العلاقة بين السرعة والضغط في الأنظمة الحقيقية
من الناحية العملية، فإن العلاقة بين الضغط والسرعة ليست خطية تمامًا بسبب:
- قيود التدفق: يؤثر حجم الصمامات والمنافذ على السرعة القصوى التي يمكن تحقيقها
- تأثيرات الانضغاطية: الهواء قابل للانضغاط، مما يتسبب في تأخر التسارع
- ظاهرة انزلاق العصا: تتغير خصائص الاحتكاك بتغير السرعة
- تأثيرات القصور الذاتي: تسارع الكتلة يتطلب قوة/ضغطًا إضافيًا
كيف تحسب أقصى تسارع ممكن في الأسطوانات الهوائية؟
يعد فهم حدود التسارع أمرًا بالغ الأهمية لمنع الصدمات المفرطة والاهتزازات والفشل المبكر للمكونات في الأنظمة الهوائية.
يتم حساب أقصى تسارع ممكن في أسطوانة تعمل بالهواء المضغوط باستخدام a = (P × A - F - Fr)/m، حيث a هو التسارع، وP هو الضغط، وA هو مساحة المكبس، وF هو الحمل الخارجي، وF هو مقاومة الاحتكاك، وm هو الكتلة المتحركة. تحدد هذه المعادلة الحدود الفيزيائية لمدى سرعة بدء المشغل الهوائي للحركة أو إيقافها.
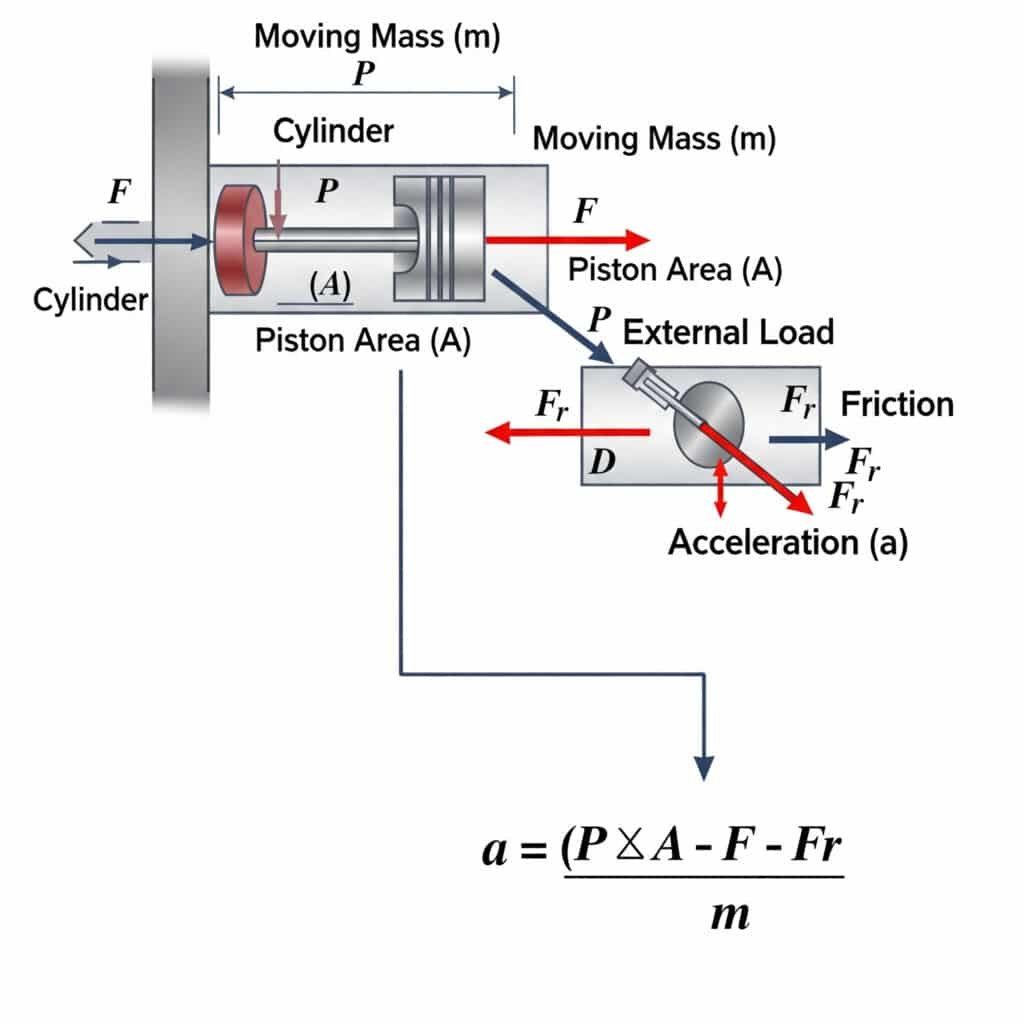
إن حدود التسارع النظرية لها آثار عملية كبيرة على تصميم النظام واختيار المكونات.
اشتقاق معادلة حد التسارع
تأتي معادلة حد التسارع من قانون نيوتن الثاني2 (F = ma):
- القوة المحصلة المتاحة للتسارع هي: Fnet = Fالضغط - التحميل - الاحتكاك
- ضغط F = P × A
- إذن: a = Fnet/m = (P × A - F - F - Fr)/م
حدود التسارع العملية لأنواع الأسطوانات المختلفة
تصميمات الأسطوانات المختلفة لها حدود تسارع عملية مختلفة:
| نوع الاسطوانة | التسارع الأقصى النموذجي | العوامل المقيدة |
|---|---|---|
| أسطوانة قضيب قياسية | 10-15 م/ثانية 10-15 م/ثانية² | التواء القضيب، أحمال التحميل |
| أسطوانة بدون قضيب (مغناطيسية) | 8-12 م/ثانية م² | قوة الاقتران المغناطيسي |
| أسطوانة بدون قضيب (ميكانيكية) | 15-25 م/ثانية م² | تصميم مانع التسرب/المحمل، الاحتكاك الداخلي |
| أسطوانة التوجيه | 20-30 م/ثانية م² | صلابة نظام التوجيه، قدرة التحمل |
| أسطوانة التأثير | 50-100 م/ثانية 50-100 م/ثانية | مصممة خصيصاً للتسارع العالي |
اعتبارات الكتلة في حسابات التسارع
عند حساب العجلة، من الضروري تضمين جميع الكتل المتحركة:
- تجميع المكبس: يشمل المكبس وموانع التسرب وعناصر التوصيل
- كتلة الحمولة: الحمولة الخارجية التي يتم نقلها
- الكتلة الفعالة للهواء المتحرك: غالبًا ما تكون ضئيلة ولكنها ذات صلة في التطبيقات عالية السرعة
- كتلة مضافة بسبب مكونات التركيب: الأقواس، وأجهزة الاستشعار، إلخ.
لقد ساعدت ذات مرة عميلاً في فرنسا كان يعاني من أعطال غامضة في نظام الأسطوانة بدون قضيب. كان حجم الأسطوانة مناسبًا للحمولة المعلنة البالغة 15 كجم، ولكنها كانت تتعطل باستمرار بعد بضعة آلاف من الدورات.
بعد التحقيق، اكتشفنا أنه أهمل حساب كتلة 12 كجم من لوحة التثبيت والملحقات. كانت الكتلة المتحركة الفعلية ضعف ما قام بحسابه تقريبًا، مما تسبب في قوى تسارع تجاوزت حدود تصميم الأسطوانة. بعد الترقية إلى أسطوانة أكبر، توقفت الأعطال تمامًا.
طرق التحكم في التسارع
للتحكم في التسارع ضمن الحدود الآمنة:
- صمامات التحكم في التدفق: الحد من معدل التدفق أثناء الحركة الأولية
- الصمامات التناسبية: توفير زيادة الضغط المتحكم فيه
- تسارع متعدد المراحل: استخدام زيادات الضغط المتدرج
- التخميد الميكانيكي: إضافة ممتصات صدمات خارجية
- تحكم إلكتروني: الاستخدام الأنظمة المؤازرة الهوائية المؤازرة3 مع ردود فعل التسارع
ما أهمية وقت التوسيد وكيف يتم حسابه؟
يعد التبطين المناسب في نهاية الشوط أمرًا ضروريًا لمنع تلف الصدمات وتقليل الضوضاء وإطالة عمر الأسطوانات الهوائية. يساعد فهم وقت التوسيد المهندسين على تصميم أنظمة توازن بين وقت الدورة وطول عمر المكونات.
يتم حساب زمن التوسيد في الأسطوانات الهوائية باستخدام المعادلة t = √(2s/a)، حيث t هو الزمن، وs هو طول شوط التوسيد، وa هو التباطؤ. يمثل هذا الوقت المدة التي يستغرقها تباطؤ الكتلة المتحركة بأمان قبل التصادم، وهو أمر بالغ الأهمية لمنع تلف الأسطوانة والمكونات المرفقة.

دعونا نستكشف الجوانب العملية لحسابات زمن التوسيد وآثارها على تصميم النظام.
الفيزياء الكامنة وراء التوسيد الهوائي
توسيد هوائي يعمل من خلال ضغط الهواء المتحكم به والعادم المقيد:
- عند دخول المكبس إلى حجرة الوسادة، يكون مسار العادم مقيدًا
- ينضغط الهواء المحتجز، مما يؤدي إلى زيادة الضغط الخلفي
- هذا الضغط الخلفي يخلق قوة مضادة تبطئ المكبس
- يعتمد شكل التباطؤ على تصميم الوسادة وتعديلها
حساب وقت التوسيد الأمثل
يوازن وقت التبطين الأمثل بين الوقاية من الصدمات وكفاءة وقت الدورة:
| المعلمة | الصيغة | مثال على ذلك |
|---|---|---|
| مسافة التوسيد | بناءً على تصميم الأسطوانة | 15 مم (نموذجي لتجويف 40 مم) |
| التباطؤ المطلوب | a = v²/(2s) | بالنسبة إلى v=0.5 م/ث، s=15 مم: a = 8.33 م/ث² |
| وقت التوسيد | ر = √(2س/أ) | t = √(2×0.015/0.015/8.33) = 0.06 ثانية |
| تراكم الضغط | P = P₀(V₀/V)^ γ | يعتمد على هندسة حجرة الوسادة |
العوامل المؤثرة على أداء التبطين
تؤثر عدة عوامل على أداء التبطين الفعلي:
- تصميم مانع تسرب الوسادة: يؤثر على تسرب الهواء أثناء التبطين
- تعديل صمام الإبرة: يتحكم في معدل تقييد العادم
- الكتلة المتحركة: الأحمال الأثقل تتطلب وقتاً أطول للتوسيد
- سرعة الاقتراب: تتطلب السرعات العالية مسافة وسادة أطول
- ضغط التشغيل: يؤثر على القوة المضادة القصوى المتاحة
أنواع الوسائد وتطبيقاتها
آليات التبطين المختلفة مناسبة للاستخدامات المختلفة:
| نوع التوسيد | الخصائص | أفضل التطبيقات |
|---|---|---|
| توسيد ثابت | بسيطة وغير قابلة للتعديل | أحمال خفيفة، تشغيل متناسق |
| توسيد قابل للتعديل | قابل للضبط بصمامات إبرية | أحمال متفاوتة وتطبيقات مرنة |
| توسيد ذاتي الضبط | يتكيف مع الظروف المختلفة | تغيير السرعات والأحمال |
| ممتصات صدمات خارجية | امتصاص عالي للطاقة | أحمال ثقيلة، سرعات عالية |
| توسيد إلكتروني | تباطؤ يتم التحكم فيه بدقة | الأنظمة المؤازرة الهوائية المؤازرة |
دراسة حالة: تحسين التوسيد في التطبيقات ذات الدورة العالية
عملت مؤخرًا مع توماس، وهو مهندس تصميم في شركة تصنيع مكونات السيارات في ألمانيا. كان خط التجميع الخاص به يستخدم أسطوانات بدون قضبان تعمل بمعدل 45 دورة في الدقيقة، ولكنه كان يعاني من أعطال متكررة في مانع التسرب وتلف في قوس التثبيت.
كشف التحليل أن وقت التوسيد كان قصيرًا جدًا بالنسبة للكتلة المتحركة، مما تسبب في قوى تصادم تقارب 3G في كل نهاية شوط. من خلال زيادة شوط التوسيد من 12 مم إلى 20 مم وتحسين إعدادات صمام الإبرة، قمنا بتمديد زمن التوسيد من 0.04 ثانية إلى 0.07 ثانية.
أدى هذا التغيير الذي يبدو صغيرًا إلى تقليل قوى الصدم بأكثر من 601 تيرابايت 3 تيرابايت، وإزالة تلف الدعامة تمامًا، وإطالة عمر مانع التسرب من 3 أشهر إلى أكثر من عام - كل ذلك مع الحفاظ على وقت الدورة المطلوب.
إجراء عملي لتعديل التوسيد عملياً
للحصول على أداء توسيد مثالي في الأسطوانات بدون قضيب:
- ابدأ بصمامات الوسادة مفتوحة بالكامل (الحد الأدنى من التقييد)
- أغلق صمام الوسادة تدريجياً حتى يتم تحقيق تباطؤ سلس
- اختبار مع الحد الأدنى والأقصى للأحمال المتوقعة
- تحقق من أداء التبطين عبر نطاق السرعة الكامل
- استمع إلى أصوات الصدمات التي تشير إلى عدم كفاية التبطين
- قياس زمن التباطؤ الفعلي لتأكيد الحسابات
الخاتمة
يعد فهم مبادئ حركية المكبس - بدءًا من متطلبات الضغط للسرعة الثابتة إلى حدود التسارع وحسابات زمن التوسيد - أمرًا ضروريًا لتصميم أنظمة هوائية فعالة وموثوقة. من خلال تطبيق هذه المبادئ على تطبيقات الأسطوانات بدون قضيب، يمكنك تحسين الأداء وتقليل استهلاك الطاقة وإطالة عمر المكونات بشكل كبير.
الأسئلة الشائعة حول حركية المكبس في الأنظمة الهوائية
ما هو الضغط الذي أحتاجه لسرعة أسطوانة معينة؟
يعتمد الضغط اللازم على الحمل والاحتكاك ومساحة الأسطوانة. احسبه باستخدام P = (F + Fr)/A، حيث F هي قوة الحمل الخارجي، وF هي قوة الحمل الخارجي، وF هي مقاومة الاحتكاك، وA هي مساحة المكبس. بالنسبة لأسطوانة نموذجية بدون قضيب تحرّك حمولة وزنها 10 كجم أفقيًا، ستحتاج إلى 1.5-2 بار تقريبًا لحركة مستقرة بسرعات معتدلة.
ما مدى سرعة تسارع الأسطوانة الهوائية؟
يتم حساب التسارع الأقصى للأسطوانة الهوائية باستخدام a = (P × A - F - Fr)/م. يمكن أن تحقق الأسطوانات النموذجية غير القضبان تسارعًا يتراوح بين 10 و25 م/ثانية حسب التصميم. ويترجم هذا إلى الوصول إلى سرعة 0.5 م/ثانية في حوالي 20-50 مللي ثانية في الظروف المثلى.
ما هي العوامل التي تحد من السرعة القصوى للأسطوانة بدون قضيب؟
تكون السرعة القصوى محدودة بسعة تدفق الصمام، وحجم إمداد الهواء، وحجم المنفذ، وقدرات التوسيد، وتصميم مانع التسرب. ومعظم الأسطوانات القياسية بدون قضيب مصممة لسرعات قصوى تتراوح بين 0.8 و1.5 م/ثانية، على الرغم من أن التصميمات المتخصصة عالية السرعة يمكن أن تصل إلى 2-3 م/ثانية.
كيف يمكنني حساب التبطين المناسب لاستخدامي؟
قم بحساب التوسيد المناسب من خلال تحديد الطاقة الحركية (KE = ½mv²) للحمل المتحرك والتأكد من قدرة نظام التوسيد على امتصاص هذه الطاقة. يجب حساب زمن التبطين باستخدام t = √(2s/a)، حيث s هي مسافة التبطين وa هو معدل التباطؤ المطلوب.
ماذا يحدث إذا تسارعت الأسطوانة الهوائية بسرعة كبيرة؟
يمكن أن يسبب التسارع المفرط إجهادًا ميكانيكيًا على مكونات التركيب، وتآكل مانع التسرب قبل الأوان، وزيادة الاهتزاز والضوضاء، واحتمال إزاحة الحمل أو تلفه، وانخفاض دقة النظام. ويمكن أن يؤدي أيضًا إلى حركة متشنجة تؤثر على جودة المنتج في التطبيقات الدقيقة.
كيف يؤثر اتجاه الحمل على الضغط المطلوب للحركة؟
يؤثر اتجاه الحمولة بشكل كبير على متطلبات الضغط. تتطلب الأحمال العمودية التي تتحرك ضد الجاذبية ضغطًا إضافيًا للتغلب على قوة الجاذبية (P = F/A + Fg/A + Fr/A). تحتاج الأحمال الأفقية فقط للتغلب على الاحتكاك والقصور الذاتي. تقع الأحمال المائلة بين هذين النقيضين بناءً على جيب الزاوية.
-
يقدم شرحًا تأسيسيًا لعلم الحركة، وهو فرع الميكانيكا الذي يصف حركة الأجسام دون النظر إلى القوى المسببة للحركة.
إشارة إدخال إلكترونية، مما يتيح تحكماً هوائياً متقدماً. ↩ -
تفاصيل قانون نيوتن الثاني (F=ma)، وهو المبدأ الأساسي للفيزياء الذي يربط القوة المؤثرة على جسم ما بكتلته وعجلته، وهو أساس جميع الحسابات الديناميكية. ↩
-
يصف تقنية المؤازرة الهوائية المؤازرة، وهي تقنية تحكم متقدمة تجمع بين قوة الهوائية الهوائية ودقة التحكم الإلكتروني مغلق الحلقة لتحقيق تحديد المواقع وملامح الحركة بدقة عالية. ↩


