هل تعاني باستمرار مع حسابات الأنظمة الهوائية؟ يواجه العديد من المهندسين نفس المشكلة عند تصميم أو استكشاف أخطاء الأنظمة الهوائية وإصلاحها. والخبر السار هو أن إتقان بعض المعادلات الرئيسية يمكن أن يحل معظم التحديات الهوائية الخاصة بك.
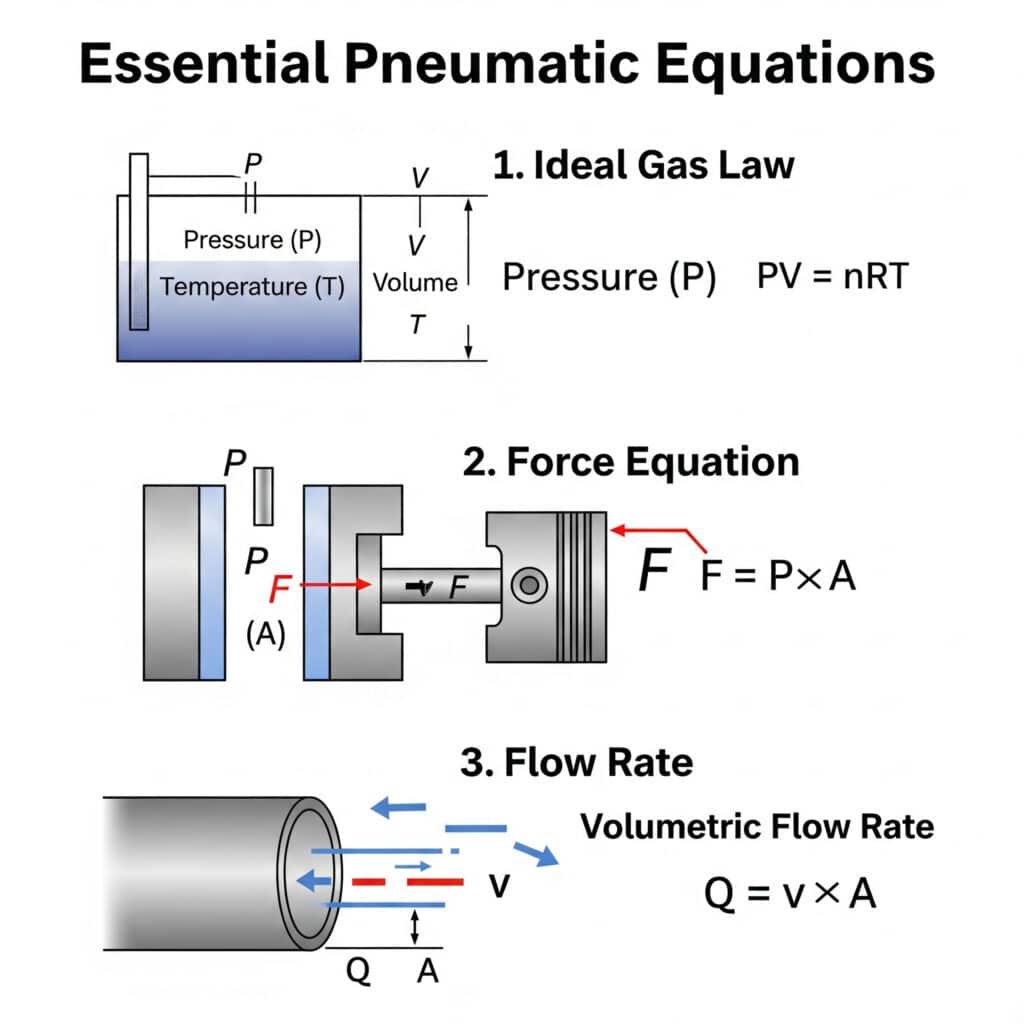
تتضمن معادلات النقل الهوائي الأساسية التي يجب أن يعرفها كل مهندس ما يلي قانون الغاز المثالي (PV = nRT)1ومعادلة القوة (F = P × A)، وعلاقة معدل التدفق (Q = v × A). يسمح فهم هذه الأساسيات بتصميم نظام دقيق واستكشاف الأخطاء وإصلاحها.
لقد أمضيت أكثر من 15 عامًا في العمل مع الأنظمة الهوائية في شركة Bepto، ورأيت عن كثب كيف يمكن لفهم هذه المعادلات الأساسية أن يوفر آلاف الدولارات من وقت التعطل ويمنع أخطاء التصميم المكلفة.
جدول المحتويات
- اشتقاق معادلة الغاز: ما أهمية PV = nRT في الأنظمة الهوائية؟
- كيف ترتبط القوة والضغط والمساحة في الأسطوانات الهوائية؟
- ما العلاقة بين معدل التدفق والسرعة في الأنظمة الهوائية؟
- الخاتمة
- الأسئلة الشائعة حول معادلات النقل الهوائي
اشتقاق معادلة الغاز: ما أهمية PV = nRT في الأنظمة الهوائية؟
عند تصميم الأنظمة الهوائية، فإن فهم كيفية تصرف الغازات في ظل ظروف مختلفة أمر بالغ الأهمية. يمكن أن تعني هذه المعرفة الفرق بين نظام يعمل بشكل موثوق ونظام يفشل بشكل غير متوقع.
قانون الغاز المثالي (PV = nRT) أساسي للأنظمة الهوائية لأنه يصف كيفية تفاعل الضغط والحجم ودرجة الحرارة. وتساعد هذه العلاقة المهندسين على التنبؤ بسلوك الهواء في الأسطوانات الخالية من القضبان والمكونات الهوائية الأخرى في ظل ظروف تشغيل مختلفة.

قد يبدو قانون الغاز المثالي مفهومًا نظريًا من دروس الفيزياء، لكن له تطبيقات عملية مباشرة في الأنظمة الهوائية. دعوني أقوم بتقسيم ذلك إلى مصطلحات أكثر عملية.
فهم المتغيرات في PV = nRT
| متغير | المعنى | التطبيق الهوائي |
|---|---|---|
| P | الضغط | ضغط التشغيل في نظامك |
| V | الحجم | حجم حجرة الهواء في الأسطوانات |
| n | عدد الشامات | كمية الهواء في النظام |
| R | ثابت الغاز2 | الثابت العام (8.314 جول/مول-ك) |
| T | درجة الحرارة | درجة حرارة التشغيل |
كيف تؤثر درجة الحرارة على الأداء الهوائي
يمكن أن تؤثر الاختلافات في درجات الحرارة بشكل كبير على أداء النظام الهوائي. في العام الماضي، اتصل بي أحد عملائنا في ألمانيا، هانز، بشأن الأداء غير المتسق في نظام الأسطوانات بدون قضيب. كان النظام يعمل بشكل مثالي في الصباح ولكنه فقد الطاقة في فترة ما بعد الظهر.
بعد تحليل إعداده، اكتشفنا أن النظام كان معرضًا لأشعة الشمس المباشرة، مما تسبب في زيادة درجة الحرارة بمقدار 15 درجة مئوية. وباستخدام قانون الغاز المثالي، حسبنا أن هذا التغير في درجة الحرارة كان يسبب تغيرًا في الضغط يبلغ حوالي 51 تيرابايت 3 تيرابايت. قمنا بتركيب عازل مناسب، وتم حل المشكلة على الفور.
التطبيقات العملية لقانون الغازات في التصميم الهوائي
عند تصميم الأنظمة الهوائية مع أسطوانات بدون قضيبفإن قانون الغاز يساعدنا:
- حساب تغيرات الضغط الناتجة عن تقلبات درجات الحرارة
- تحديد الاحتياجات الحجمية لخزانات الهواء
- توقع تغيرات ناتج القوة في ظل ظروف مختلفة
- قياس حجم الضواغط بشكل مناسب للتطبيق
كيف ترتبط القوة والضغط والمساحة في الأسطوانات الهوائية؟
يعد فهم العلاقة بين القوة والضغط والمساحة أمرًا ضروريًا عند اختيار الأسطوانة المناسبة بدون قضيب لاستخدامك. تضمن لك هذه المعرفة حصولك على الأداء الذي تحتاجه دون الإفراط في الإنفاق.
إن العلاقة بين القوة والضغط والمساحة3 في الأسطوانات التي تعمل بالهواء المضغوط تُعرَّف بالمعادلة F = P × A، حيث F هي القوة (N)، وP هي الضغط (Pa)، وA هي المساحة الفعالة (m²). تسمح هذه المعادلة للمهندسين بحساب ناتج القوة الدقيقة للأسطوانات بدون قضيب عند ضغوط تشغيل مختلفة.
هذه المعادلة البسيطة هي أساس جميع حسابات القوة الهوائية، ولكن هناك العديد من الاعتبارات العملية التي يغفل عنها العديد من المهندسين.
حسابات المساحة الفعالة لأنواع الأسطوانات المختلفة
تختلف المساحة الفعالة حسب نوع الأسطوانة:
| نوع الاسطوانة | حساب المساحة الفعالة | الملاحظات |
|---|---|---|
| أحادية المفعول | أ = πr² | منطقة التجويف الكامل |
| مزدوج المفعول (التمديد) | أ = πr² | منطقة التجويف الكامل |
| مزدوج المفعول (التراجع) | أ = π(r² - r'²) | r' هو نصف قطر القضيب |
| أسطوانة بدون قضيب | أ = πr² | متناسق في كلا الاتجاهين |
عوامل كفاءة القوة في العالم الحقيقي
من الناحية العملية، يتأثر ناتج القوة الفعلي بما يلي:
- خسائر الاحتكاك: عادةً 3-20% حسب تصميم الختم
- انخفاض الضغط: يمكن أن يقلل الضغط الفعال بنسبة 5-10%
- المؤثرات الديناميكية: يمكن أن تقلل قوى التسارع من القوة المتاحة
أتذكر العمل مع سارة، وهي مهندسة ميكانيكية من شركة تعبئة وتغليف في المملكة المتحدة. كانت تقوم بتصميم ماكينة جديدة وحسبت أنها تحتاج إلى أسطوانة بدون قضيب بتجويف 63 مم لتحقيق القوة المطلوبة. ومع ذلك، لم تأخذ في الحسبان خسائر الاحتكاك.
أوصينا بزيادة أسطوانة ذات تجويف 80 مم، مما وفر قوة إضافية كافية للتغلب على الاحتكاك مع الحفاظ على أدائها المطلوب. هذا التعديل البسيط أنقذها من إعادة تصميم مكلفة بعد التركيب.
مقارنة ناتج القوة النظري مقابل ناتج القوة الفعلي
عند اختيار أسطوانات بدون قضيب، أوصي دائماً بما يلي:
- احسب القوة النظرية باستخدام F = P × A
- تطبيق عامل أمان 25% لمعظم التطبيقات
- تحقق من الحسابات مع بيانات الأداء الفعلي من الشركة المصنعة
- النظر في ظروف التحميل الديناميكية إن أمكن
ما العلاقة بين معدل التدفق والسرعة في الأنظمة الهوائية؟
يعد معدل التدفق والسرعة من المعلمات الهامة التي تحدد مدى سرعة استجابة نظامك الهوائي. يساعد فهم هذه العلاقة على منع الأداء البطيء ويضمن تلبية نظامك لمتطلبات زمن الدورة.
العلاقة بين معدل التدفق (Q) والسرعة (v)4 في الأنظمة التي تعمل بالهواء المضغوط تُعرَّف بالمعادلة Q = v × A، حيث Q هو معدل التدفق الحجمي، وv هي سرعة الهواء، وA هي مساحة المقطع العرضي للممر. هذه المعادلة ضرورية لتحديد حجم خطوط الهواء والصمامات بشكل صحيح.
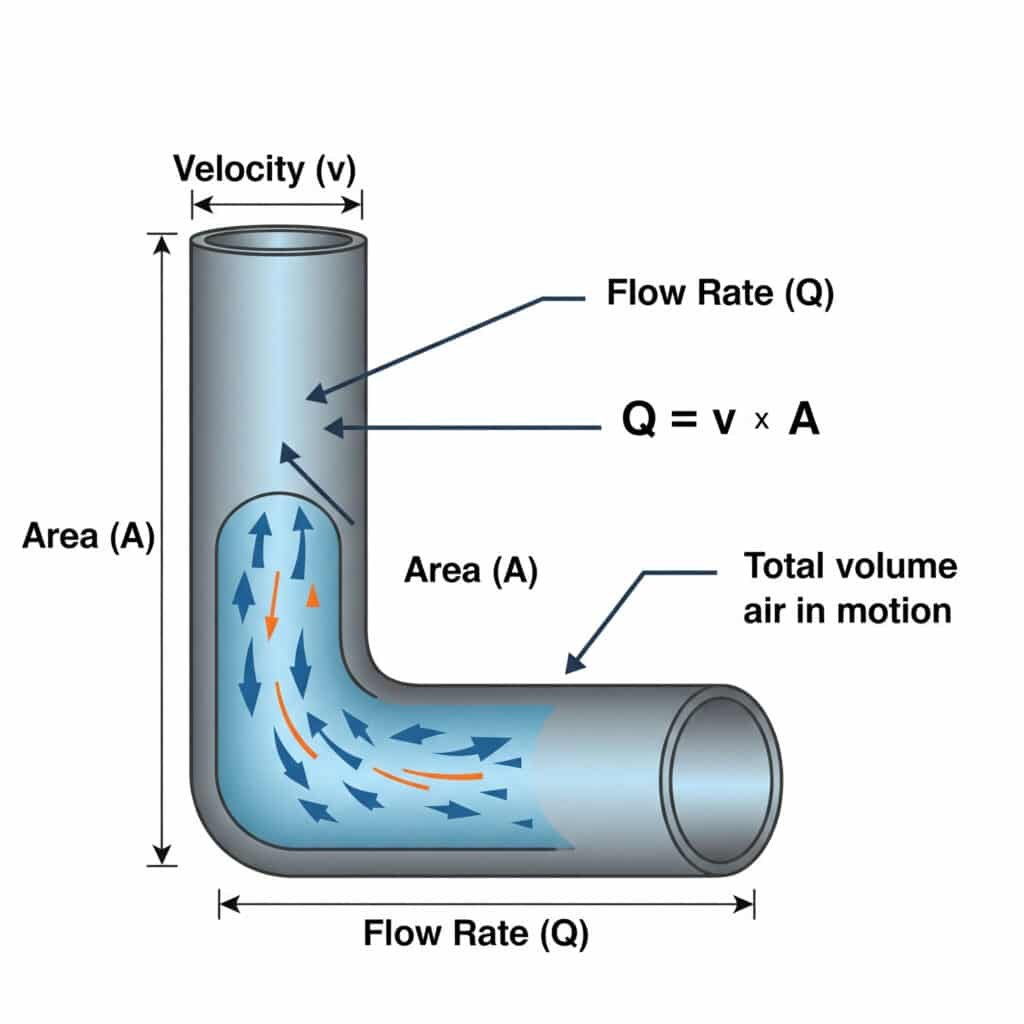
تنشأ العديد من مشكلات النظام الهوائي من التحجيم غير المناسب لمكونات إمداد الهواء. دعونا نستكشف كيف تؤثر هذه المعادلة على الأداء في العالم الحقيقي.
معدلات التدفق الحرجة للمكونات الهوائية الشائعة
المكونات المختلفة لها متطلبات تدفق مختلفة:
| المكوّن | متطلبات معدل التدفق النموذجي | تأثير تصغير الحجم الصغير |
|---|---|---|
| أسطوانة بدون قضيب (تجويف 25 مم) | 15-30 لتر/دقيقة | بطء التشغيل، وانخفاض القوة |
| أسطوانة بدون قضيب (تجويف 63 مم) | 60-120 لتر/دقيقة | حركة غير متناسقة |
| صمام تحكم اتجاهي | تختلف حسب الحجم | انخفاض الضغط، استجابة بطيئة |
| وحدة تحضير الهواء | إجمالي النظام + 30% | تقلبات الضغط |
كيف يؤثر قطر الأنبوب على أداء النظام
قطر خطوط الهواء لديك له تأثير كبير على أداء النظام:
- انخفاض الضغط: تزداد مع زيادة مربع السرعة
- وقت الاستجابة: الخطوط الأصغر تعني سرعة أعلى ولكن مقاومة أكبر
- كفاءة الطاقة: الخطوط الأكبر حجمًا تقلل من انخفاض الضغط ولكنها تزيد من التكلفة
حساب أحجام الخطوط المناسبة للأنظمة الهوائية
لتحديد حجم أنابيب الهواء بشكل صحيح لاستخدام الأسطوانة بدون قضيب:
- تحديد معدل التدفق المطلوب بناءً على حجم الأسطوانة وزمن الدورة
- حساب الحد الأقصى المسموح به لانخفاض الضغط (عادةً 0.1 بار أو أقل)
- حدد قطر الخط الذي يحافظ على سرعة أقل من 15-20 م/ثانية
- تحقق من سعة تدفق الصمام (قيمة Cv أو Kv5) يطابق متطلبات النظام
لقد ساعدت ذات مرة عميلًا في فرنسا كان يعاني من بطء حركة الأسطوانة على الرغم من امتلاكه ضاغطًا كبيرًا. لم تكن المشكلة عدم كفاية توليد الهواء - بل كانت المشكلة أن أنابيبه مقاس 6 مم كانت تخلق مقاومة مفرطة. أدت الترقية إلى أنابيب 10 مم إلى حل المشكلة على الفور، مما أدى إلى زيادة معدل دورة ماكينته بمقدار 40%.
الخاتمة
يوفر فهم هذه المعادلات الهوائية الأساسية الثلاث - قانون الغاز المثالي، والعلاقة بين القوة والضغط والمساحة، والعلاقة بين معدل التدفق والسرعة - الأساس لتصميم نظام هوائي ناجح. من خلال تطبيق هذه المبادئ، يمكنك اختيار مكونات الأسطوانة بدون قضيب المناسبة، واستكشاف المشكلات وإصلاحها بفعالية، وتحسين أداء النظام.
الأسئلة الشائعة حول معادلات النقل الهوائي
ما هو قانون الغاز المثالي ولماذا هو مهم للأنظمة الهوائية؟
يصف قانون الغاز المثالي (PV = nRT) كيفية ارتباط الضغط والحجم ودرجة الحرارة وكمية الغاز في نظام هوائي. وهو مهم لأنه يساعد المهندسين على التنبؤ بكيفية تأثير الظروف المتغيرة (خاصة درجة الحرارة) على أداء النظام ومتطلبات الضغط.
كيف يمكنني حساب قوة الخرج لأسطوانة بدون قضيب؟
احسب ناتج القوة بضرب الضغط في المساحة الفعالة (F = P × A). بالنسبة لأسطوانة بدون قضيب، تكون المساحة الفعالة هي نفسها في كلا الاتجاهين، مما يجعل حسابات القوة أبسط من الأسطوانات التقليدية التي لها قوى تمديد وسحب مختلفة.
ما الفرق بين معدل التدفق والسرعة في الأنظمة الهوائية؟
معدل التدفق هو حجم الهواء الذي يتحرك عبر نظام ما لكل وحدة زمنية (عادةً بوحدة اللتر/الدقيقة)، بينما السرعة هي السرعة التي يتحرك بها الهواء عبر ممر (بالمتر/الثانية). وهما مرتبطان بالمعادلة Q = v × A، حيث A هي مساحة المقطع العرضي للممر.
كيف تؤثر درجة الحرارة على أداء النظام الهوائي؟
تؤثر درجة الحرارة بشكل مباشر على الضغط وفقًا لقانون الغاز المثالي. يمكن أن تؤدي زيادة 10 درجات مئوية في درجة الحرارة إلى زيادة الضغط بحوالي 3.51 تيرابايت 3 تيرابايت إذا ظل الحجم ثابتًا. وهذا يمكن أن يسبب تغيرات في الضغط، ويؤثر على أداء مانع التسرب، ويغير ناتج القوة في الأسطوانات بدون قضيب.
ما هو السبب الأكثر شيوعًا لانخفاض الضغط في الأنظمة الهوائية؟
الأسباب الأكثر شيوعًا لانخفاض الضغط هي أنابيب الهواء الأصغر حجمًا، والتجهيزات المقيدة، وعدم كفاية سعة تدفق الصمام. ووفقًا لمعادلة معدل التدفق، تتطلب الممرات الأصغر سرعة هواء أعلى، مما يزيد من المقاومة وانخفاض الضغط أضعافًا مضاعفة.
كيف يمكنني قياس حجم أنابيب الهواء بشكل صحيح لأسطوانة بدون قضيب؟
قم بتحديد حجم أنابيب الهواء عن طريق حساب معدل التدفق المطلوب بناءً على حجم الأسطوانة وزمن الدورة، ثم اختر قطر خط يحافظ على سرعة الهواء أقل من 15-20 م/ثانية لتقليل انخفاض الضغط. بالنسبة لمعظم تطبيقات الأسطوانات بدون قضيب، توفر خطوط 8-12 مم توازنًا جيدًا بين الأداء والتكلفة.
-
يقدم شرحًا تفصيليًا لقانون الغاز المثالي، وهو معادلة الحالة الأساسية لغاز مثالي افتراضي يقارب سلوك العديد من الغازات في ظروف مختلفة. ↩
-
يشرح دور ثابت الغاز العام (R) وقيمته في قانون الغاز المثالي الذي يُستخدم كثابت فيزيائي يربط بين مقاييس الطاقة ومقاييس درجة الحرارة. ↩
-
يقدم شرحًا تأسيسيًا للضغط، الذي يُعرَّف بأنه القوة المؤثرة عموديًا على سطح جسم ما لكل وحدة مساحة تتوزع عليها هذه القوة. ↩
-
تفاصيل مبدأ معادلة الاستمرارية وهو مفهوم أساسي في ديناميكا الموائع ينص على أنه بالنسبة لمائع غير قابل للانضغاط، يجب أن يكون معدل السريان الكتلي ثابتاً من مقطع عرضي لأنبوب إلى آخر. ↩
-
يوفر تعريفًا تقنيًا لمعامل التدفق (Cv) ومعامل التدفق (Kv)، وهما قيمتان قياسيتان تستخدمان لمقارنة سعات التدفق للصمامات المختلفة. ↩


