Máte potíže s předvídáním skutečného výkonu pneumatického válce? Mnoho inženýrů špatně odhaduje silové výkony a požadavky na tlak, což vede k poruchám systému a nákladným odstávkám. Existuje však jednoduchý způsob, jak tyto výpočty zvládnout.
Pneumatické válce fungují na základních fyzikálních principech, především na základě Pascalův zákon1, která říká, že tlak působící na uzavřenou kapalinu se přenáší rovnoměrně ve všech směrech. To nám umožňuje vypočítat sílu ve válci vynásobením tlaku efektivní plochou pístu, přičemž průtoky a jednotky tlaku vyžadují přesné převody pro přesný návrh systému.
Více než deset let jsem pomáhal zákazníkům optimalizovat jejich pneumatické systémy a viděl jsem, jak může pochopení těchto základních principů změnit spolehlivost systému. Podělím se s vámi o praktické znalosti, které vám pomohou vyhnout se běžným chybám, s nimiž se setkávám každý den.
Obsah
- Jak Pascalův zákon určuje silový výkon válce?
- Jaký je vztah mezi průtokem vzduchu a tlakem ve válcích?
- Proč je pro návrh systému důležité porozumět převodu jednotek tlaku?
- Závěr
- Časté dotazy o fyzice v pneumatických systémech
Jak Pascalův zákon určuje silový výkon válce?
Pochopení Pascalova zákona je základem pro předvídání a optimalizaci výkonu válce v jakémkoli pneumatickém systému.
Pascalův zákon říká, že tlak působící na kapalinu v uzavřeném systému se přenáší rovnoměrně do celé kapaliny. U pneumatických válců to znamená, že výstupní síla se rovná tlaku vynásobenému efektivní plochou pístu (F = P × A). Tento jednoduchý vztah je základem pro všechny výpočty síly ve válci.
Odvození výpočtu síly
Rozebereme si matematické odvození výpočtů síly válce:
Základní rovnice síly
Základní rovnice pro sílu válce je:
F = P × A
Kde:
- F = výstupní síla (N)
- P = tlak (Pa)
- A = účinná plocha pístu (m²)
Úvahy o efektivní oblasti
Účinná plocha se liší v závislosti na typu a směru válce:
| Typ válce | Prodlužovací síla | Síla zatažení |
|---|---|---|
| Jednočinný | P × A | Pouze síla pružiny |
| Dvojčinný (standardní) | P × A | P × (A - a) |
| Dvojčinný (beztaktní) | P × A | P × A |
Kde:
- A = plná plocha pístu
- a = plocha průřezu tyče
Jednou jsem konzultoval výrobní závod v Ohiu, který se potýkal s nedostatečnou silou při lisování. Jejich výpočty se zdály být na papíře správné, ale skutečný výkon byl nedostatečný. Po prošetření jsem zjistil, že používají manometr2 ve svých výpočtech místo absolutního tlaku a nezohlednili plochu tyče při zatahování. Po přepočítání pomocí správného vzorce a hodnot tlaku jsme byli schopni správně dimenzovat jejich systém a zvýšit produktivitu o 23%.
Praktické příklady výpočtu síly
Podívejme se na několik reálných výpočtů:
Příklad 1: Roztahovací síla ve standardním válci
Pro válec s:
- Průměr otvoru = 50 mm (poloměr = 25 mm = 0,025 m)
- Provozní tlak = 6 barů (600 000 Pa)
Oblast pístu je:
A = π × r² = π × (0,025)² = 0,001963 m²
Rozšiřující síla je:
F = P × A = 600 000 Pa × 0,001963 m² = 1 178 N ≈ 118 kg síly
Příklad 2: Vtahovací síla ve stejném válci
Je-li průměr tyče 20 mm (poloměr = 10 mm = 0,01 m):
Oblast tyče je:
a = π × r² = π × (0,01)² = 0,000314 m²
Efektivní plocha zatažení je:
A - a = 0,001963 - 0,000314 = 0,001649 m²
Zatahovací síla je:
F = P × (A - a) = 600 000 Pa × 0,001649 m² = 989 N ≈ síla 99 kg
Faktory účinnosti v reálných aplikacích
V praktických aplikacích ovlivňuje teoretický výpočet síly několik faktorů:
Ztráty třením
Tření mezi těsněním pístu a stěnou válce snižuje účinnou sílu:
| Typ těsnění | Typický faktor účinnosti |
|---|---|
| Standardní NBR | 0.85-0.90 |
| PTFE s nízkým třením | 0.90-0.95 |
| Zestárlá/opotřebovaná těsnění | 0.70-0.85 |
Praktická rovnice síly
Přesnější rovnice reálné síly je:
F_actual = η × P × A
Kde:
- η (eta) = faktor účinnosti (obvykle 0,85-0,95)
Jaký je vztah mezi průtokem vzduchu a tlakem ve válcích?
Pochopení vztahu mezi průtokem a tlakem je zásadní pro dimenzování systémů přívodu vzduchu a předvídání otáček válce.
Průtok a tlak vzduchu v pneumatických systémech jsou v nepřímém vztahu - s rostoucím tlakem obvykle klesá průtok. Tento vztah se řídí plynárenskými zákony a je ovlivněn omezeními, teplotou a objemem systému. Správný provoz válce vyžaduje vyvážení těchto faktorů, aby bylo dosaženo požadované rychlosti a síly.
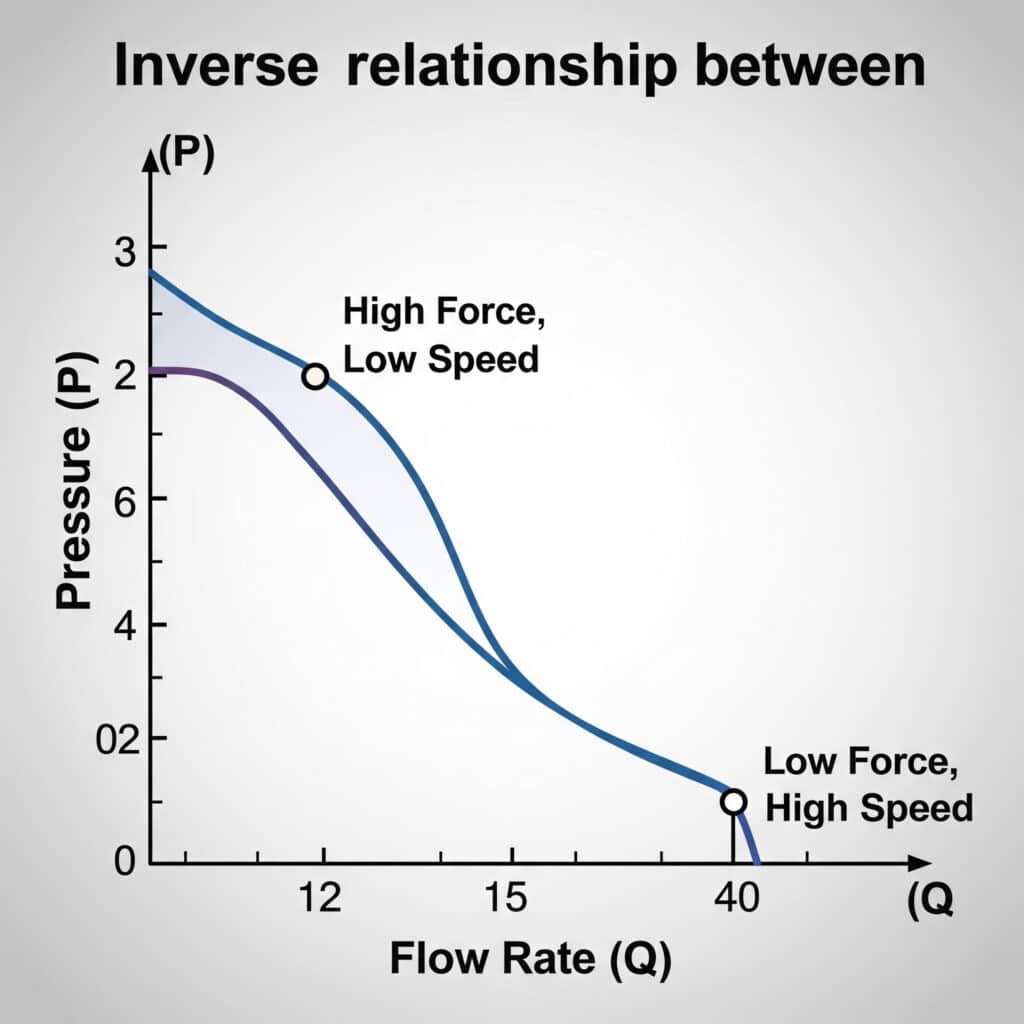
Převodní tabulka průtoku a tlaku
Tato praktická referenční tabulka ukazuje vztah mezi průtokem a tlakovou ztrátou na různých součástech systému:
| Velikost potrubí (mm) | Průtok (l/min) | Pokles tlaku (bar/meter) při 6 barech napájení |
|---|---|---|
| 4 | 100 | 0.15 |
| 4 | 200 | 0.45 |
| 4 | 300 | 0.90 |
| 6 | 200 | 0.08 |
| 6 | 400 | 0.25 |
| 6 | 600 | 0.50 |
| 8 | 400 | 0.06 |
| 8 | 800 | 0.18 |
| 8 | 1200 | 0.35 |
| 10 | 600 | 0.04 |
| 10 | 1200 | 0.12 |
| 10 | 1800 | 0.24 |
Matematika proudění a tlaku
Vztah mezi průtokem a tlakem se řídí několika plynovými zákony:
Poiseuilleova rovnice3 pro laminární proudění
Pro laminární proudění potrubím:
Q = (π × r⁴ × ΔP) / (8 × η × L)
Kde:
- Q = objemový průtok
- r = poloměr potrubí
- ΔP = rozdíl tlaků
- η = dynamická viskozita
- L = délka potrubí
Koeficient průtoku (Cv)4 Metoda
U součástí, jako jsou ventily:
Q = Cv × √ΔP
Kde:
- Q = průtok
- Cv = průtokový součinitel
- ΔP = tlaková ztráta na součásti
Výpočet otáček válce
Rychlost pneumatického válce závisí na průtoku a ploše válce:
v = Q / A
Kde:
- v = rychlost válce (m/s)
- Q = průtok (m³/s)
- A = plocha pístu (m²)
Během nedávného projektu v balírně ve Francii jsem se setkal se situací, kdy se beztlakové válce klienta pohybovaly příliš pomalu, přestože měly dostatečný tlak. Analýzou jejich systému pomocí našich výpočtů průtoku a tlaku jsme zjistili poddimenzované přívodní potrubí, které způsobovalo značný pokles tlaku. Po modernizaci z 6mm na 10mm potrubí se jejich doba cyklu zlepšila o 40%, čímž se výrazně zvýšila výrobní kapacita.
Kritická hlediska toku
Vztah průtoku a tlaku v pneumatických systémech ovlivňuje několik faktorů:
Fenomén udušeného proudění5
Pokud tlakový poměr překročí kritickou hodnotu (přibližně 0,53 pro vzduch), průtok se "přiškrtí" a nemůže se zvýšit bez ohledu na snížení tlaku za proudem.
Vliv teploty
Průtok je ovlivněn teplotou podle vztahu:
Q₂ = Q₁ × √(T₂/T₁)
Kde:
- Q₁, Q₂ = průtoky při různých teplotách
- T₁, T₂ = absolutní teploty
Proč je pro návrh systému důležité porozumět převodu jednotek tlaku?
Orientace v různých tlakových jednotkách používaných po celém světě je nezbytná pro správný návrh systému a mezinárodní kompatibilitu.
Přepočet jednotek tlaku je velmi důležitý, protože pneumatické komponenty a specifikace používají různé jednotky v závislosti na regionu a odvětví. Nesprávná interpretace jednotek může vést k významným chybám ve výpočtech s potenciálně nebezpečnými důsledky. Převod mezi absolutním, manometrickým a diferenčním tlakem přidává další vrstvu složitosti.
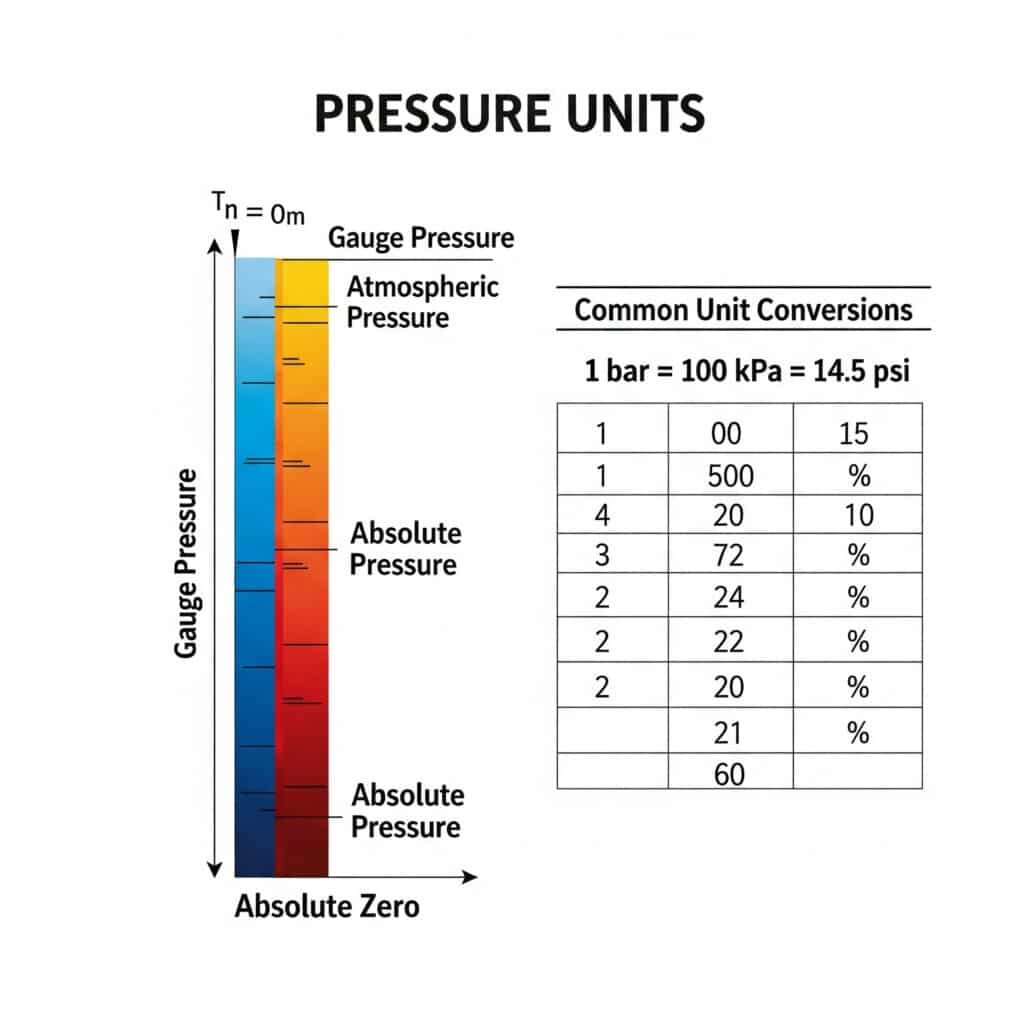
Průvodce převodem jednotek absolutního tlaku
Tato přehledná převodní tabulka pomáhá orientovat se v různých jednotkách tlaku používaných po celém světě:
| Jednotka | Symbol | Ekvivalent v Pa | Ekvivalent v barech | Ekvivalent v psi |
|---|---|---|---|---|
| Pascal | Pa | 1 | 1 × 10-⁵ | 1.45 × 10-⁴ |
| Bar | bar | 1 × 10⁵ | 1 | 14.5038 |
| Libra na čtvereční palec | psi | 6,894.76 | 0.0689476 | 1 |
| Kilogram síly na čtvereční centimetr | kgf/cm² | 98,066.5 | 0.980665 | 14.2233 |
| Megapascal | MPa | 1 × 10⁶ | 10 | 145.038 |
| Atmosféra | atm | 101,325 | 1.01325 | 14.6959 |
| Torr | Torr | 133.322 | 0.00133322 | 0.0193368 |
| Milimetr rtuti | mmHg | 133.322 | 0.00133322 | 0.0193368 |
| Palec vody | vH₂O | 249.089 | 0.00249089 | 0.0361274 |
Absolutní vs. měřicí tlak
Zásadní je pochopení rozdílu mezi absolutním a manometrickým tlakem:
Kalkulačka pro převod tlaku
Převodník jednotek tlaku
Převodník průtoku válců
Převodní vzorce
- P_absolute = P_gauge + P_atmospheric
- P_gauge = P_absolute - P_atmospheric
Kde je standardní atmosférický tlak přibližně:
- 1,01325 baru
- 14,7 psi
- 101 325 Pa
Kdysi jsem spolupracoval s týmem inženýrů v Německu, kteří si zakoupili naše beztlakové válce, ale hlásili, že nedosahují očekávané síly. Po vyřešení problémů jsme zjistili, že používají naše grafy síly (které jsou založeny na manometrickém tlaku), ale zadávají hodnoty absolutního tlaku. Toto jednoduché nedorozumění způsobovalo, že jejich očekávaná síla byla o 1 bar nižší. Po vyjasnění referenčního tlaku jejich systém fungoval přesně podle zadání.
Praktické příklady převodů
Projděme si několik běžných scénářů převodu:
Příklad 1: Převod pracovního tlaku v jednotkách
Válec dimenzovaný na maximální pracovní tlak 0,7 MPa:
V baru:
0,7 MPa × 10 bar/MPa = 7 barů
V psi:
0,7 MPa × 145,038 psi/MPa = 101,5 psi
Příklad 2: Převod z manometru na absolutní tlak
Systém pracující s manometrickým tlakem 6 barů:
V absolutním tlaku (bar):
6 bar_gauge + 1,01325 bar_atmospheric = 7,01325 bar_absolute
Příklad 3: Převod z kgf/cm² na MPa
Japonský válec s hodnotou 7 kgf/cm²:
V MPa:
7 kgf/cm² × 0,0980665 MPa/(kgf/cm²) = 0,686 MPa
Preference regionálních tlakových jednotek
V různých oblastech se obvykle používají různé jednotky tlaku:
| Region | Běžné tlakové jednotky |
|---|---|
| Severní Amerika | psi, inHg, inH₂O |
| Evropa | bar, Pa, mbar |
| Japonsko | kgf/cm², MPa |
| Čína | MPa, bar |
| UK | bar, psi, Pa |
Měření tlaku v dokumentaci
Při dokumentování specifikací tlaku je nezbytné jasně uvést:
- Číselná hodnota
- Měrná jednotka
- Ať už se jedná o manometrický (g) nebo absolutní (a) tlak.
Například:
- 6 bar_g (manometrický tlak, 6 barů nad atmosférickým)
- 7,01 bar_a (absolutní tlak, celkový tlak včetně atmosférického)
Závěr
Pochopení fyzikálních principů pneumatických válců - od výpočtů sil podle Pascalova zákona až po vztahy mezi průtokem a tlakem a převody jednotek tlaku - je nezbytné pro správný návrh systému a řešení problémů. Tyto základní principy pomáhají zajistit, aby vaše pneumatické systémy spolehlivě a efektivně poskytovaly očekávaný výkon.
Časté dotazy o fyzice v pneumatických systémech
Jak vypočítám výstupní sílu pneumatického válce bez tyčí?
Chcete-li vypočítat výstupní sílu beztlakového pneumatického válce, vynásobte provozní tlak efektivní plochou pístu (F = P × A). Například beztlakový válec s otvorem 50 mm (plocha 0,001963 m²) pracující při tlaku 6 barů (600 000 Pa) vyvine sílu přibližně 1 178 N. Na rozdíl od tradičních válců mají bezprutové válce obvykle stejnou účinnou plochu v obou směrech.
Jak vypočítám výstupní sílu pneumatického válce bez tyčí?
Chcete-li vypočítat výstupní sílu beztlakového pneumatického válce, vynásobte provozní tlak efektivní plochou pístu (F = P × A). Například beztlakový válec s otvorem 50 mm (plocha 0,001963 m²) pracující při tlaku 6 barů (600 000 Pa) vyvine sílu přibližně 1 178 N. Na rozdíl od tradičních válců mají bezprutové válce obvykle stejnou účinnou plochu v obou směrech.
Jaký je rozdíl mezi manometrickým a absolutním tlakem?
Měřicí tlak (bar_g, psi_g) měří tlak vzhledem k atmosférickému tlaku, přičemž atmosférický tlak je nulový. Absolutní tlak (bar_a, psi_a) měří tlak vzhledem k dokonalému vakuu, které je nulové. Chcete-li převést manometrický tlak na absolutní, přičtěte k hodnotě manometrického tlaku atmosférický tlak (přibližně 1,01325 baru nebo 14,7 psi).
Jak ovlivňuje proudění vzduchu otáčky válce?
Otáčky válce jsou přímo úměrné průtoku vzduchu a nepřímo úměrné ploše pístu (v = Q/A). Nedostatečný průtok způsobený poddimenzovaným přívodním potrubím, omezujícími armaturami nebo nevhodnými ventily omezuje otáčky válce bez ohledu na tlak. Například průtok 20 litrů za sekundu válcem s plochou pístu 0,002 m² způsobí rychlost 10 m/s.
Proč se pneumatické válce někdy pohybují pomaleji, než bylo vypočteno?
Pneumatické válce se mohou pohybovat pomaleji, než bylo vypočteno, a to v důsledku několika faktorů: omezení přívodu vzduchu způsobující pokles tlaku, vnitřní tření způsobené těsněním, mechanické zatížení překračující výpočty, netěsnost snižující efektivní tlak nebo vliv teploty na hustotu vzduchu. Kromě toho průtokové koeficienty ventilů často omezují skutečný průtok, který je k dispozici válci.
Jak převést různé jednotky tlaku pro mezinárodní specifikace?
Pro převod mezi jednotkami tlaku použijte násobení: 1 bar = 100 000 Pa = 0,1 MPa = 14,5038 psi = 1,01972 kgf/cm². Vždy si ověřte, zda je tlak uveden jako manometrický nebo absolutní, protože toto rozlišení může významně ovlivnit výpočty. Například 6 bar_g se za standardních atmosférických podmínek rovná 7,01325 bar_a.
Jaký je vztah mezi velikostí otvoru válce a výkonem?
Vztah mezi velikostí otvoru válce a silovým výkonem je kvadratický - zdvojnásobením průměru otvoru se silový výkon zvýší čtyřikrát (protože plocha = π × r²). Například při provozním tlaku 6 barů vyvíjí válec s otvorem 40 mm sílu přibližně 754 N, zatímco válec s otvorem 80 mm vyvíjí sílu přibližně 3 016 N, což je téměř čtyřikrát více.
-
Podrobně vysvětluje Pascalův zákon, základní princip mechaniky tekutin, který je základem hydraulického a pneumatického přenosu energie. ↩
-
Nabízí jasnou definici a srovnání měřicího a absolutního tlaku, což je zásadní rozdíl pro přesné technické výpočty, protože měřicí tlak je relativní vůči atmosférickému tlaku. ↩
-
Vysvětluje odvození a použití Poiseuilleova zákona, který popisuje tlakovou ztrátu nestlačitelné newtonovské kapaliny proudící dlouhou válcovou trubkou v laminárním režimu. ↩
-
Poskytuje technickou definici průtokového součinitele (Cv), což je imperiální měření, které poskytuje standardizovaný způsob porovnávání průtokových kapacit různých ventilů. ↩
-
Podrobnosti o fyzikálních zákonitostech proudění s přívodem, což je podmínka dynamiky tekutin, která omezuje hmotnostní průtok stlačitelné tekutiny omezením, když rychlost dosáhne rychlosti zvuku. ↩
English 
Deutsch 
Français 
Italiano 
Español 
Português 
Русский 
العربية 
日本語 
한국어 
Bahasa Indonesia 
Türkçe 
Nederlands 
Ελληνικά 
Български 
Čeština 
Dansk 
Eesti 
Suomi 
Magyar 
Lietuvių kalba 
Latviešu valoda 
Polski 
Română 
Svenska 
Slovenčina 
Slovenščina 
Norsk bokmål 
Українська