
Dotkli jste se někdy pneumatický válec po nepřetržitém provozu a překvapilo vás, jak je horký? Toto teplo není jen nepříjemnost - představuje plýtvání energií, sníženou účinnost a potenciální problémy se spolehlivostí, které mohou stát váš provoz tisíce.
K přenosu tepla v pneumatických systémech dochází třemi mechanismy: vedením skrze materiály součástí, konvekcí mezi povrchy a vzduchem a sáláním z horkých povrchů. Pochopení a optimalizace těchto principů může snížit provozní teploty o 15-30%, prodloužit životnost součástí až o 40% a zlepšit energetickou účinnost o 5-15%.
Minulý měsíc jsem poskytoval konzultace pro potravinářský závod v Georgii, kde jejich beztlakové lahve selhávaly každé 3-4 měsíce kvůli tepelným problémům. Jejich tým údržby jednoduše vyměňoval komponenty, aniž by řešil hlavní příčinu. Uplatněním správných principů přenosu tepla jsme snížili provozní teploty o 22 °C a prodloužili životnost komponent na více než rok. Dovolte mi, abych vám ukázal, jak jsme to dokázali - a jak můžete stejné principy aplikovat na své systémy.
Obsah
- Výpočet součinitele vodivosti: Jak se teplo pohybuje vašimi součástmi?
- Metody zvyšování konvekce: Jaké techniky maximalizují přenos tepla ze vzduchu na povrch?
- Model účinnosti vyzařování: Kdy má tepelné vyzařování v pneumatických systémech význam?
- Závěr
- Často kladené otázky o přenosu tepla v pneumatických systémech
Výpočet součinitele vodivosti: Jak se teplo pohybuje vašimi součástmi?
Hlavním mechanismem přenosu tepla v pevných pneumatických součástech je vedení. Pochopení způsobu výpočtu a optimalizace součinitelů vedení je zásadní pro řízení teploty systému.
Součinitel tepelné vodivosti lze vypočítat pomocí následujícího postupu Fourierův zákon1: q = -k(dT/dx), kde q je tepelný tok (W/m²), k je tepelná vodivost (W/m-K) a dT/dx je teplotní gradient. U pneumatických součástí závisí účinná vodivost na výběru materiálu, kvalitě rozhraní a geometrických faktorech, které ovlivňují délku tepelné dráhy a plochu průřezu.
Vzpomínám si, jak jsem řešil problémy na výrobní lince v Tennessee, kde předčasně selhávala ložiska válců bez tyčí. Tým údržby vyzkoušel několik maziv, ale bez úspěchu. Když jsme analyzovali vodivé cesty, zjistili jsme, že na rozhraní ložiska a pouzdra je tepelné úzké hrdlo. Zlepšením povrchové úpravy a nanesením tepelně vodivé směsi jsme zvýšili efektivní součinitel vodivosti o 340% a poruchy jsme zcela odstranili.
Základní rovnice vedení
Rozebereme si klíčové rovnice pro výpočet vedení v pneumatických komponentech:
Fourierův zákon pro vedení tepla
Základní rovnice pro vedení tepla zní:
q = -k(dT/dx)
Kde:
- q = tepelný tok (W/m²)
- k = součinitel tepelné vodivosti (W/m-K)
- dT/dx = teplotní gradient (K/m)
Pro jednoduchý jednorozměrný případ s konstantním průřezem:
Q = kA(T₁-T₂)/L
Kde:
- Q = rychlost přenosu tepla (W)
- A = plocha průřezu (m²)
- T₁, T₂ = teploty na obou koncích (K)
- L = délka tepelné cesty (m)
Koncepce tepelného odporu
U složitých geometrií je často praktičtější metoda tepelného odporu:
R = L/(kA)
Kde:
- R = tepelný odpor (K/W)
Pro systémy s více komponenty v sérii:
Rtotal = R₁ + R₂ + R₃ + ... + Rₙ
A rychlost přestupu tepla je:
Q = ΔT/Rcelkem
Srovnání tepelné vodivosti materiálů
| Materiál | Tepelná vodivost (W/m-K) | Relativní vodivost | Běžné aplikace |
|---|---|---|---|
| Hliník | 205-250 | Vysoká | Válce, chladiče |
| Ocel | 36-54 | Střední | Konstrukční prvky |
| Nerezová ocel | 14-16 | Nízká a střední úroveň | Korozivní prostředí |
| Bronz | 26-50 | Střední | Ložiska, pouzdra |
| PTFE | 0.25 | Velmi nízká | Těsnění, ložiska |
| Nitrilový kaučuk | 0.13 | Velmi nízká | O-kroužky, těsnění |
| Vzduch (nehybný) | 0.026 | Extrémně nízká | Výplň mezer |
| Tepelná pasta | 3-8 | Nízká | Materiál rozhraní |
Kontaktní odpor v pneumatických sestavách
Na rozhraních mezi součástmi má kontaktní odpor významný vliv na přenos tepla:
Rkontakt = 1/(hc × A)
Kde:
- hc = kontaktní součinitel (W/m²-K)
- A = kontaktní plocha (m²)
Mezi faktory ovlivňující kontaktní odpor patří:
- Drsnost povrchu: Drsnější povrchy mají menší skutečnou kontaktní plochu
- Kontaktní tlak: Vyšší tlak zvyšuje efektivní kontaktní plochu
- Materiály rozhraní: Tepelné směsi vyplňují vzduchové mezery
- Čistota povrchu: Kontaminanty mohou zvýšit odolnost
Případová studie: Tepelná optimalizace válce bez tyčí
Pro magnetický válec bez tyčí, který má tepelné problémy:
| Komponenta | Originální design | Optimalizovaný design | Zlepšení |
|---|---|---|---|
| Těleso válce | Eloxovaný hliník | Stejný materiál, vylepšená povrchová úprava | 15% lepší vedení |
| Rozhraní ložisek | Kontakt kov na kov | Přidaná tepelná směs | 340% lepší vedení |
| Montážní držáky | Lakovaná ocel | Holý hliník | 280% lepší vedení |
| Celkový tepelný odpor | 2,8 K/W | 0,7 K/W | Redukce 75% |
| Provozní teplota | 78°C | 56°C | Snížení o 22 °C |
| Životnost součásti | 4 měsíce | >12 měsíců | 3× zlepšení |
Praktické techniky optimalizace vedení
Na základě zkušeností se stovkami pneumatických systémů uvádím nejúčinnější přístupy ke zlepšení vodivosti:
Optimalizace rozhraní
- Povrchová úprava: Zlepšení hladkosti krycího povrchu na Ra 0,4-0,8 μm.
- Materiály tepelného rozhraní2: Použijte vhodné směsi (3-8 W/m-K).
- Utahovací moment spojovacího materiálu: Zajistěte správné utažení pro optimální přítlak
- Čistota: Před montáží odstraňte všechny oleje a nečistoty
Strategie výběru materiálu
- Kritické tepelné dráhy: Použijte vysoce vodivé materiály (hliník, měď).
- Tepelné přestávky: Záměrně používejte materiály s nízkou vodivostí, abyste izolovali teplo.
- Kompozitní přístupy: Kombinace materiálů pro dosažení optimálního poměru výkon/cena
- Anizotropní materiály: V případě potřeby využijte směrovou vodivost
Geometrická optimalizace
- Délka tepelné dráhy: Minimalizace vzdálenosti mezi zdroji tepla a chladiči
- Plocha průřezu: Maximalizujte plochu kolmou na tepelný tok
- Tepelné překážky: Identifikujte a odstraňte zúžení tepelné dráhy
- Nadbytečné cesty: Vytvoření více paralelních vodivých tras
Metody zvyšování konvekce: Jaké techniky maximalizují přenos tepla ze vzduchu na povrch?
Konvekce je často limitujícím faktorem chlazení pneumatických systémů. Zlepšení konvekčního přenosu tepla může výrazně zlepšit tepelné řízení a výkon systému.
Následuje konvektivní přenos tepla Newtonův zákon ochlazování3: Q = hA(Ts-T∞), kde h je koeficient konvekce (W/m²-K), A je plocha povrchu a (Ts-T∞) je rozdíl teplot mezi povrchem a kapalinou. Metody vylepšení zahrnují zvětšení plochy povrchu pomocí žeber, zlepšení rychlosti proudění tekutiny pomocí usměrněného proudění vzduchu a optimalizaci vlastností povrchu pro podporu turbulentních mezních vrstev.
Během auditu energetické účinnosti v balírně v Arizoně jsem narazil na pneumatický systém pracující v prostředí s teplotou 43 °C. Jejich válce bez tyčí se přehřívaly, přestože splňovaly všechny požadavky na údržbu. Zavedením cíleného zlepšení konvekce - přidáním malých hliníkových žeber a ventilátoru s nízkou spotřebou energie - jsme zvýšili konvekční součinitel o 450%. Tím se provozní teploty snížily z nebezpečných hodnot na hodnoty v rámci specifikací bez jakýchkoli větších úprav systému.
Základy konvekčního přenosu tepla
Základní rovnice pro konvektivní přenos tepla zní:
Q = hA(Ts-T∞)
Kde:
- Q = rychlost přenosu tepla (W)
- h = součinitel konvekce (W/m²-K)
- A = plocha povrchu (m²)
- Ts = povrchová teplota (K)
- T∞ = teplota kapaliny (vzduchu) (K)
Koeficient konvekce h závisí na více faktorech:
- Vlastnosti kapaliny (hustota, viskozita, tepelná vodivost)
- Charakteristiky proudění (rychlost, turbulence)
- Geometrie a orientace povrchu
- Režim proudění (přirozená vs. nucená konvekce)
Přirozená vs. nucená konvekce
| Parametr | Přirozená konvekce | Nucená konvekce | Důsledky |
|---|---|---|---|
| Typická hodnota h | 5-25 W/m²-K | 25-250 W/m²-K | Nucená konvekce může být 10× účinnější. |
| Hnací síla | Vztlak (rozdíl teplot) | Vnější tlak (ventilátory, dmychadla) | Nucená konvekce je méně závislá na teplotě |
| Vzor toku | Vertikální proudění podél povrchů | Směrové na základě mechanismu vynucování | Nucený průtok lze optimalizovat pro konkrétní komponenty |
| Spolehlivost | Pasivní, vždy přítomný | Vyžaduje napájení a údržbu | Přirozená konvekce zajišťuje základní chlazení |
| Požadavky na prostor | Vyžaduje volný prostor pro cirkulaci vzduchu | Vyžaduje prostor pro vzduchotechnické jednotky a potrubí. | Nucené systémy vyžadují více plánování |
Techniky zvyšování konvekce
Zvětšení plochy
Zvětšení efektivní plochy díky:
Ploutve a rozšířené plochy
- Kolíkové ploutve: Všesměrové proudění vzduchu, zvětšení plochy 150-300%
- Deskové ploutve: Směrové proudění vzduchu, zvětšení plochy 200-500%
- Vlnité povrchy: 50-150% nárůst plochyZdrsnění povrchu
- Mikrotextury: Efektivní zvětšení plochy: 5-15%
- Drážkované povrchy: zvýšení o 10-30% plus efekty mezní vrstvy
- Drážkované vzory: 15-40% zvýšení se směrovými výhodami
Manipulace s tokem
Zlepšení vlastností proudění vzduchu prostřednictvím:
Systémy nuceného větrání
- Ventilátory: Směrové proudění vzduchu, 200-600% h zlepšení
- Dmychadla: Vysokotlaký průtok, 300-800% h zlepšení
- Trysky stlačeného vzduchu: 400-1000% místní zlepšení hOptimalizace průtokové cesty
- Baffles: Přímý přístup vzduchu ke kritickým komponentům
- Venturiho efekt: Urychlují vzduch nad určitými povrchy
- Vírové generátory: Vytvářejte turbulence pro narušení mezní vrstvy
Úpravy povrchu
Změna vlastností povrchu za účelem zvýšení konvekce:
Ošetření emisivity
- Černý oxid: Zvyšuje emisivitu na 0,7-0,9
- eloxování: Řízená emisivita od 0,4-0,9
- Barvy a nátěry: Přizpůsobitelná emisivita až 0,98Kontrola smáčivosti
- Hydrofilní nátěry: Zlepšují chlazení kapalinou
- Hydrofobní povrchy: Předcházejte problémům s kondenzací
- Vzorovaná smáčivost: Řízený tok kondenzátu
Praktický příklad implementace
Pro pneumatické válce bez tyčí, které pracují v prostředí s vysokou teplotou:
| Metoda vylepšení | Provádění | h Zlepšení | Snížení teploty |
|---|---|---|---|
| Kolíkové ploutve (6 mm) | Hliníkové příchytné lamely, rozteč 10 mm | 180% | 12°C |
| Řízené proudění vzduchu | 80mm, 2W ventilátor DC při rychlosti 1,5 m/s | 320% | 18°C |
| Povrchová úprava | Černé eloxování | 40% | 3°C |
| Kombinovaný přístup | Všechny metody integrované | 450% | 24°C |
Korelace Nusseltova čísla pro návrhové výpočty
Pro inženýrské výpočty se Nusseltovo číslo4 (Nu) poskytuje bezrozměrný přístup ke konvekci:
Nu = hL/k
Kde:
- L = charakteristická délka
- k = tepelná vodivost kapaliny
Pro nucenou konvekci nad plochou deskou:
Nu = 0,664Re^(1/2)Pr^(1/3) (laminární proudění)
Nu = 0,037Re^(4/5)Pr^(1/3) (turbulentní proudění)
Kde:
- Re = Reynoldsovo číslo (rychlost × délka × hustota / viskozita).
- Pr = Prandtlovo číslo (měrné teplo × viskozita / tepelná vodivost)
Tyto korelace umožňují inženýrům předpovídat konvekční koeficienty pro různé konfigurace a podle toho optimalizovat strategie chlazení.
Model účinnosti vyzařování: Kdy má tepelné vyzařování v pneumatických systémech význam?
Sálání je v tepelném managementu pneumatických systémů často přehlíženo, ale v mnoha aplikacích může představovat 15-30% celkového přenosu tepla. Pochopení toho, kdy a jak optimalizovat sálavý přenos tepla, je pro komplexní tepelný management klíčové.
Přenos tepla sáláním probíhá podle Stefanův-Boltzmannův zákon5: Q = εσA(T₁⁴-T₂⁴), kde ε je emisivita povrchu, σ je Stefanova-Boltzmannova konstanta, A je plocha povrchu a T₁ a T₂ jsou absolutní teploty vyzařujícího povrchu a okolí. Účinnost vyzařování v pneumatických systémech závisí především na emisivitě povrchu, teplotním rozdílu a činitelích pohledu mezi součástmi a jejich okolím.
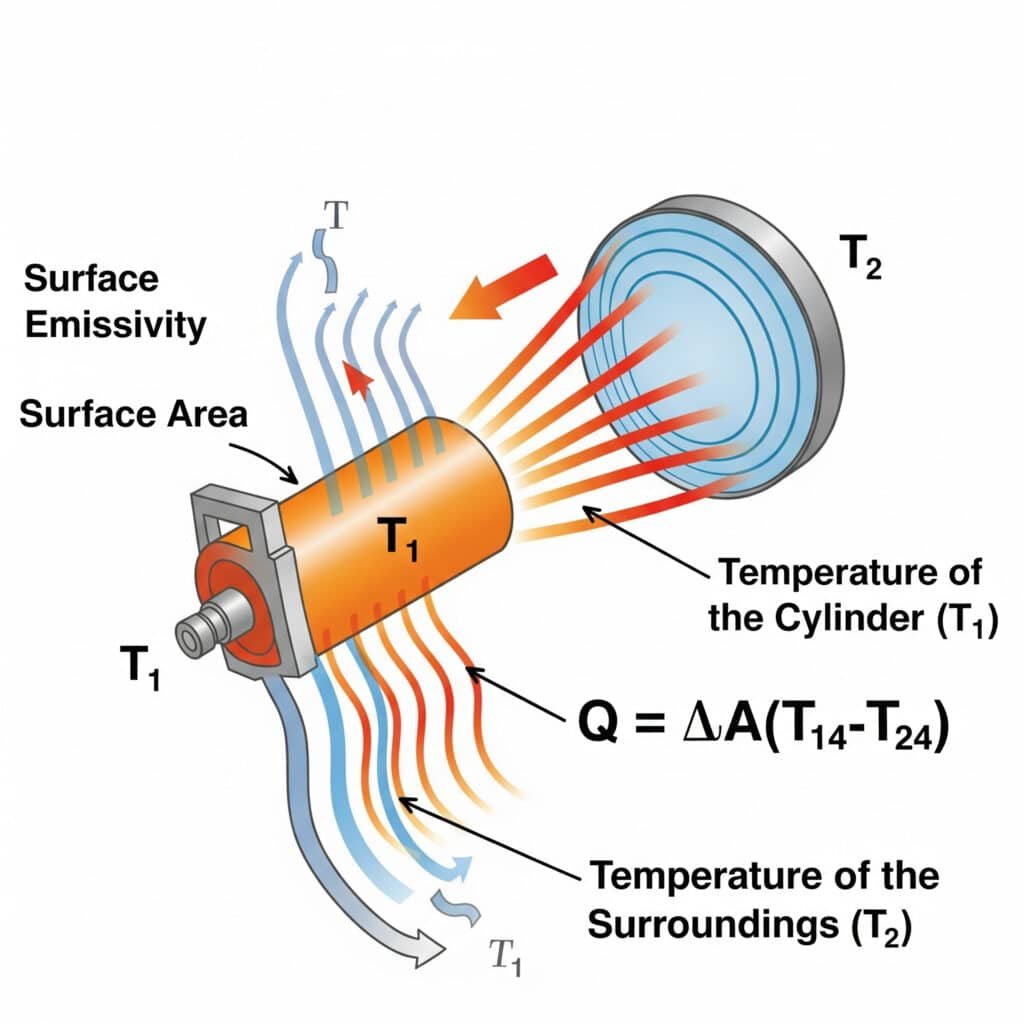
Nedávno jsem pomáhal jednomu výrobci polovodičových zařízení v Oregonu vyřešit problémy s přehříváním jeho přesných válců bez tyčí. Jejich inženýři se zaměřili výhradně na vedení a konvekci, ale přehlédli záření. Nanesením povlaku s vysokou emisivitou (zvýšení ε z 0,11 na 0,92) jsme zvýšili přenos tepla sáláním o více než 700%. Toto jednoduché pasivní řešení snížilo provozní teplotu o 9 °C bez jakýchkoli pohyblivých částí nebo spotřeby energie - což je v prostředí čistých prostor kritický požadavek.
Základy přenosu tepla sáláním
Základní rovnice pro sálavý přenos tepla zní:
Q = εσA(T₁⁴-T₂⁴)
Kde:
- Q = rychlost přenosu tepla (W)
- ε = emisivita (bezrozměrná, 0-1)
- σ = Stefanova-Boltzmannova konstanta (5,67 × 10-⁸ W/m²-K⁴)
- A = plocha povrchu (m²)
- T₁ = absolutní teplota povrchu (K)
- T₂ = absolutní teplota okolí (K)
Hodnoty emisivity povrchu pro běžné pneumatické materiály
| Materiál/povrch | Emisivita (ε) | Účinnost vyzařování | Potenciál vylepšení |
|---|---|---|---|
| Leštěný hliník | 0.04-0.06 | Velmi špatný | >1500% možné zlepšení |
| Eloxovaný hliník | 0.7-0.9 | Vynikající | Již optimalizováno |
| Nerezová ocel (leštěná) | 0.07-0.14 | Špatný | >600% možné zlepšení |
| Nerezová ocel (oxidovaná) | 0.6-0.85 | Dobrý | Možnost mírného zlepšení |
| Ocel (leštěná) | 0.07-0.10 | Špatný | Možnost zlepšení >900% |
| Ocel (oxidovaná) | 0.7-0.9 | Vynikající | Již optimalizováno |
| Lakované povrchy | 0.8-0.98 | Vynikající | Již optimalizováno |
| PTFE (bílý) | 0.8-0.9 | Vynikající | Již optimalizováno |
| Nitrilový kaučuk | 0.86-0.94 | Vynikající | Již optimalizováno |
Zobrazení faktorů
Výměna záření závisí nejen na emisivitě, ale také na geometrických vztazích mezi povrchy:
F₁₂ = Podíl záření, které opouští povrch 1 a dopadá na povrch 2.
U složitých geometrií lze faktory zobrazení vypočítat pomocí:
- Analytická řešení pro jednoduché geometrie
- Zobrazit algebru faktorů pro kombinaci známých řešení
- Numerické metody pro komplexní uspořádání
- Empirické aproximace pro praktické inženýrství
Závislost záření na teplotě
Díky teplotnímu vztahu čtvrté mocniny je záření účinné zejména při vyšších teplotách:
| Povrchová teplota | Procento přenosu tepla sáláním* |
|---|---|
| 30°C (303K) | 5-15% |
| 50°C (323K) | 10-25% |
| 75°C (348K) | 15-35% |
| 100 °C (373 K) | 25-45% |
| 150°C (423K) | 35-60% |
*Předpokládáme podmínky přirozené konvekce, ε = 0,8, okolní teplota 25 °C.
Strategie zvyšování účinnosti záření
Na základě svých zkušeností s průmyslovými pneumatickými systémy uvádím nejúčinnější přístupy ke zlepšení přenosu tepla zářením:
Modifikace emisivity povrchu
Povlaky s vysokou emisivitou
- Černý elox pro hliník (ε ≈ 0,8-0,9)
- Černý oxid pro ocel (ε ≈ 0,7-0,8)
- Speciální keramické povlaky (ε ≈ 0,9-0,98)Texturování povrchu
- Mikrodrsnění zvyšuje efektivní emisivitu
- Porézní povrchy zlepšují radiační vlastnosti
- Kombinované vylepšení emisivity/konvekce
Optimalizace životního prostředí
Řízení okolní teploty
- Stínění před horkým zařízením/procesy
- Chladné stěny/stropy pro lepší výměnu záření
- Reflexní bariéry, které směrují záření na chladnější povrchy.Zobrazení faktoru Zlepšení
- Orientace pro maximální vystavení chladným povrchům
- Odstranění blokujících předmětů
- Reflektory pro zlepšení výměny záření s chladnějšími oblastmi
Případová studie: Zlepšení radiace v přesné pneumatice
Pro vysoce přesný beztyčový válec v prostředí čistých prostor:
| Parametr | Originální design | Design se zvýšenou radiační účinností | Zlepšení |
|---|---|---|---|
| Povrchový materiál | Leštěný hliník (ε ≈ 0,06) | Hliník s keramickým povlakem (ε ≈ 0,94) | 1467% zvýšení emisivity |
| Přenos tepla sáláním | 2.1W | 32.7W | 1457% zvýšení záření |
| Provozní teplota | 68°C | 59°C | Snížení o 9 °C |
| Životnost součásti | 8 měsíců | >24 měsíců | 3× zlepšení |
| Náklady na implementaci | – | $175 na válec | Návratnost 4,2 měsíce |
Sálání vs. jiné způsoby přenosu tepla
Pro efektivní tepelný management je zásadní pochopit, kdy záření převládá:
| Stav | Dominance vedení | Převaha konvekce | Dominance záření |
|---|---|---|---|
| Teplotní rozsah | Nízká až vysoká | Nízká až střední | Střední až vysoká |
| Vlastnosti materiálu | Materiály s vysokým k | Nízký k, vysoký povrch | Vysoké ε povrchy |
| Faktory prostředí | Dobrý tepelný kontakt | Pohybující se vzduch, ventilátory | Velký teplotní rozdíl |
| Omezení prostoru | Pevné balení | Otevřené proudění vzduchu | Výhled do chladnějšího okolí |
| Nejlepší aplikace | Rozhraní složek | Obecné chlazení | Horké povrchy, vakuum, nehybný vzduch |
Závěr
Zvládnutí principů přenosu tepla - výpočet součinitele vedení, metody zvyšování konvekce a modelování účinnosti vyzařování - poskytuje základ pro efektivní řízení tepla v pneumatických systémech. Uplatněním těchto principů můžete snížit provozní teploty, prodloužit životnost součástí a zlepšit energetickou účinnost a zároveň zajistit spolehlivý provoz i v náročných podmínkách.
Často kladené otázky o přenosu tepla v pneumatických systémech
Jaký je typický nárůst teploty v pneumatických válcích během provozu?
U pneumatických válců dochází při nepřetržitém provozu obvykle k nárůstu teploty o 20-40 °C nad okolní teplotu. Toto zvýšení je důsledkem tření mezi těsněním a stěnami válce, ohřevu vzduchu při kompresi a přeměny mechanické práce na teplo. U bezprutových válců dochází často k vyššímu nárůstu teploty (30-50 °C) v důsledku jejich složitějších těsnicích systémů a soustředěného vzniku tepla v sestavě ložisko/těsnění.
Jak ovlivňuje provozní tlak vznik tepla v pneumatických systémech?
Provozní tlak má významný vliv na produkci tepla, přičemž vyšší tlaky vytvářejí více tepla prostřednictvím několika mechanismů. Každé zvýšení provozního tlaku o 1 bar obvykle zvyšuje produkci tepla o 8-12% v důsledku větších třecích sil mezi těsněními a povrchy, vyššího ohřevu při stlačení a zvýšených ztrát souvisejících s netěsnostmi. Tento vztah je přibližně lineární v běžných provozních rozsazích (3-10 barů).
Jaký je optimální způsob chlazení pneumatických součástí v různých prostředích?
Optimální způsob chlazení se liší podle prostředí: v čistém prostředí s mírnou teplotou (15-30 °C) často postačuje přirozená konvekce s vhodnými rozestupy mezi součástmi. V prostředí s vysokou teplotou (30-50 °C) je nutná nucená konvekce pomocí ventilátorů nebo stlačeného vzduchu. V extrémně horkých podmínkách (>50 °C) nebo tam, kde je omezeno proudění vzduchu, mohou být nutné aktivní metody chlazení, jako jsou termoelektrické chladiče nebo kapalinové chlazení. Ve všech případech poskytuje maximální vyzařování prostřednictvím povrchů s vysokou emisivitou dodatečné pasivní chlazení.
Jak vypočítám celkový přenos tepla z pneumatické součásti?
Vypočítejte celkový přenos tepla sečtením příspěvků jednotlivých mechanismů: Qtotal = Qconduction + Qconvection + Qradiation. Pro vedení použijte Q = kA(T₁-T₂)/L pro každou tepelnou cestu. Pro konvekci použijte Q = hA(Ts-T∞) s příslušnými konvekčními koeficienty. Pro záření použijte Q = εσA(T₁⁴-T₂⁴). Ve většině průmyslových pneumatických aplikací pracujících při teplotách 30-80 °C je přibližné rozdělení 20-40% vedení, 40-70% konvekce a 10-30% záření.
Jaký je vztah mezi teplotou a životností pneumatických součástí?
Životnost součástek exponenciálně klesá s rostoucí teplotou podle modifikovaného Arrheniova vztahu. Obecně platí, že každé zvýšení provozní teploty o 10 °C snižuje životnost těsnění a komponent o 40-50%. To znamená, že součástka pracující při teplotě 70 °C může mít pouze třetinovou životnost ve srovnání se stejnou součástkou pracující při teplotě 50 °C. Tento vztah je obzvláště kritický pro polymerní komponenty, jako jsou těsnění, ložiska a těsnění, které často určují interval údržby pneumatických systémů.
-
Poskytuje základní vysvětlení Fourierova zákona, základního principu, který popisuje vedení tepla pevnými materiály na základě jejich tepelné vodivosti a teplotního gradientu. ↩
-
Vysvětluje funkci a typy materiálů tepelného rozhraní (TIM), které se používají k vyplnění mikroskopických vzduchových mezer mezi součástmi za účelem zlepšení vedení tepla a snížení tepelného odporu. ↩
-
Podrobně se seznámí s principy Newtonova chladicího zákona, který řídí, jak se objekty ochlazují předáváním tepla okolní tekutině konvekcí, což je klíčový faktor při návrhu chlazení systému. ↩
-
Nabízí podrobný pohled na Nusseltovo číslo, kritickou bezrozměrnou veličinu v dynamice tekutin a přenosu tepla, která vyjadřuje poměr konvektivního a konduktivního přenosu tepla přes hranici. ↩
-
Popisuje Stefanův-Boltzmannův zákon, základní fyzikální princip, který kvantifikuje celkovou energii vyzářenou černým tělesem, což je nezbytné pro výpočet tepelných ztrát z horkých povrchů. ↩



