Jak vibrační rezonance ovlivňuje výkon průmyslových zařízení?

Noční můrou každého technika údržby je neočekávaná porucha zařízení. Když stroje vibrují na své přirozené frekvenci, může během několika minut dojít ke katastrofálnímu poškození. Viděl jsem, že tento problém stojí společnosti tisíce dolarů za prostoje.

Vibrační rezonance¹ nastává, když se vnější síla shoduje s vlastní frekvencí systému, což způsobuje zesílené oscilace, které mohou poškodit zařízení. Pochopení a řízení tohoto jevu je zásadní pro prevenci poruch a prodloužení životnosti strojů.

Dovolte mi, abych se s vámi podělil o krátký příběh. Minulý rok mi v panice zavolal zákazník z Německa. Jejich výrobní linka se zastavila, protože bezprutový válec prudce vibroval. Problém? Rezonance. Na konci tohoto článku už budete vědět, jak podobné problémy ve svých systémech identifikovat a jak jim předcházet.

Obsah

Vzorec pro přirozenou frekvenci: Jak vypočítat zranitelné body vašeho systému?
Model Mass-Spring: Proč je tento zjednodušený přístup tak cenný?
Optimalizace tlumicího poměru: Jaké experimenty přinášejí nejlepší výsledky?
Závěr
Časté dotazy o vibrační rezonanci

Vzorec pro přirozenou frekvenci: Jak vypočítat zranitelné body vašeho systému?

Pochopení přirozené frekvence zařízení je prvním krokem k předcházení problémům s rezonancí. Tato kritická hodnota určuje, kdy je váš systém nejvíce náchylný k problémům s vibracemi.

Na stránkách vlastní frekvence² (fn) systému lze vypočítat podle vzorce: fn = (1/2π) × √(k/m), kde k je součinitel tuhosti a m je hmotnost. Tento výpočet odhalí frekvenci, při které bude váš systém rezonovat, pokud bude vybuzen odpovídajícími vnějšími silami.

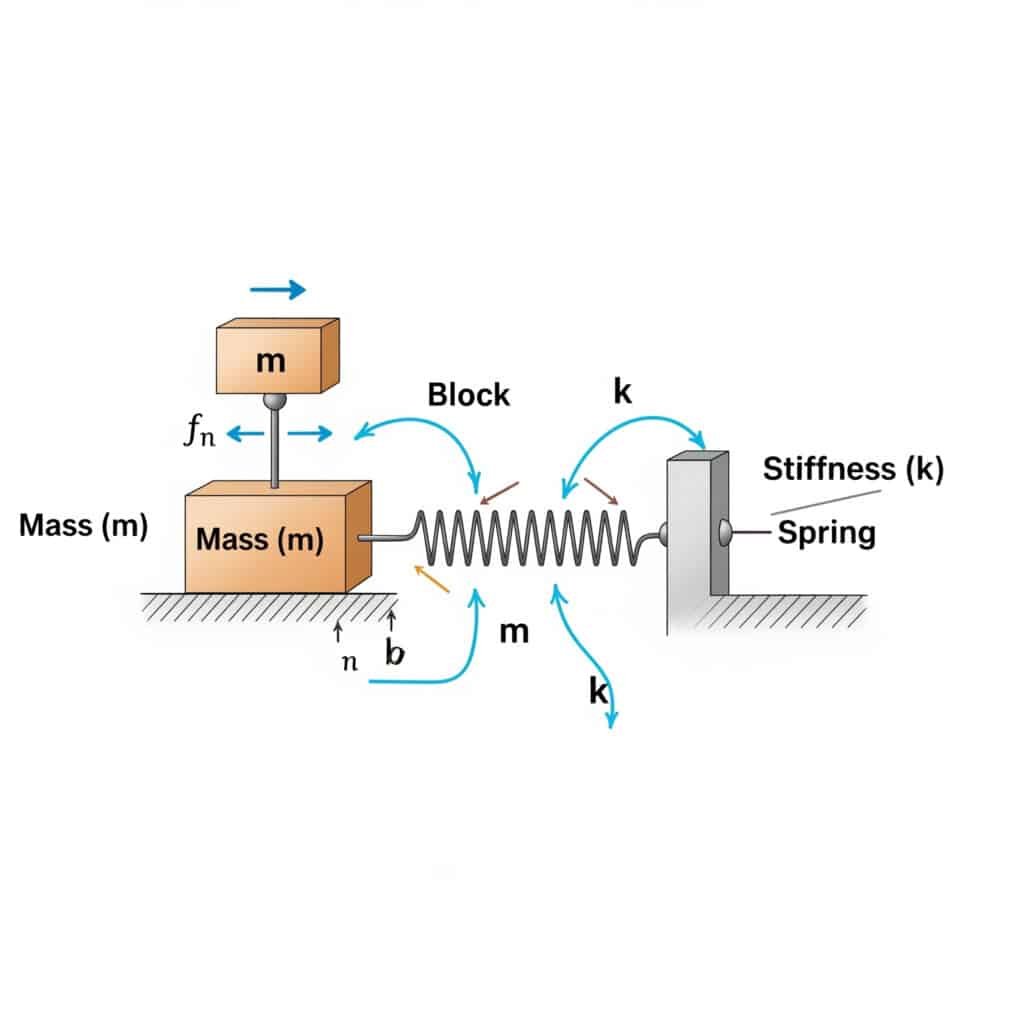
Přehledný výukový diagram vysvětlující vlastní frekvenci. Na obrázku je jednoduchý systém hmoty a pružiny, přičemž kvádr je označen jako "hmotnost (m)" a pružina jako "tuhost (k)". Pohybové čáry ukazují, že systém kmitá. Vedle diagramu je jasně zobrazen vzorec "fn = (1/2π) × √(k/m)" se šipkami, které výslovně spojují proměnné "m" a "k" v rovnici s odpovídajícími fyzikálními částmi. — vlastní frekvence

Když jsem navštívil jeden výrobní závod ve Švýcarsku, všiml jsem si, že jejich pneumatické válce bez tyčí předčasně selhávají. Jejich tým údržby nevypočítal vlastní frekvenci jejich nastavení. Po použití tohoto vzorce jsme zjistili, že jejich provozní rychlost se nebezpečně blíží vlastní frekvenci systému.

Praktické aplikace výpočtů vlastních frekvencí

Vzorec pro vlastní frekvenci není jen teoretický - má přímé využití v různých průmyslových podmínkách:

Výběr zařízení: Výběr komponentů s vlastními frekvencemi vzdálenými od provozních podmínek
Preventivní údržba: Plánování kontrol na základě profilů rizika vibrací
Řešení problémů: Identifikace hlavní příčiny neočekávaných vibrací

Běžné hodnoty přirozené frekvence pro průmyslové komponenty

Komponenta	Typický rozsah vlastních frekvencí (Hz)
Válce bez tyčí	10-50 Hz
Montážní držáky	20-100 Hz
Podpůrné struktury	5-30 Hz
Regulační ventily	40-200 Hz

Kritické faktory ovlivňující vlastní frekvenci

Výpočet vlastní frekvence se zdá být jednoduchý, ale v reálných aplikacích jej může komplikovat několik faktorů:

Nerovnoměrné rozložení hmotnosti: Většina průmyslových součástí nemá dokonale rozloženou hmotnost.
Proměnlivá tuhost: Součásti mohou mít v různých směrech různou tuhost.
Připojovací body: Způsob montáže součástí významně ovlivňuje jejich vibrační vlastnosti.
Vliv teploty: Hmotnostní i tuhostní vlastnosti se mohou měnit s teplotou.

Model Mass-Spring: Proč je tento zjednodušený přístup tak cenný?

Hmotnostně-pružinový model poskytuje intuitivní rámec pro pochopení složitých vibračních systémů. Složité stroje redukuje na základní prvky, které mohou inženýři snadno analyzovat.

Na stránkách hmotnostně pružinový model³ zjednodušuje analýzu vibrací tím, že představuje mechanické systémy jako diskrétní hmoty spojené pružinami. Tento přístup umožňuje inženýrům předpovídat chování systému, identifikovat potenciální problémy s rezonancí a vyvíjet účinná řešení bez složité matematiky.

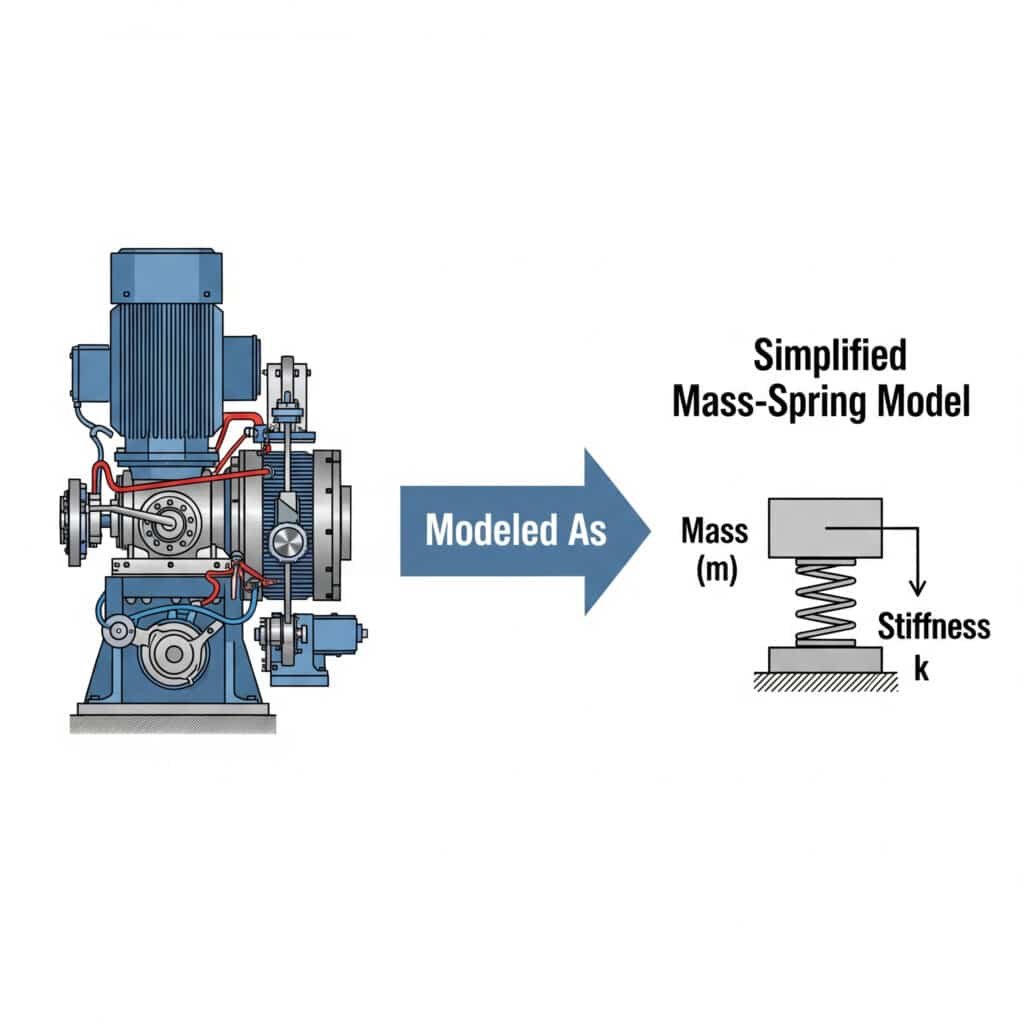
Srovnávací infografika s vysvětlením hmotnostně pružinového modelu. Vlevo pod označením "Složitý mechanický systém" je podrobná ilustrace průmyslového motoru. Velká šipka s nápisem "Modelováno jako" ukazuje doprava. Vpravo pod označením "Zjednodušený model hmoty a pružiny" je celý složitý motor znázorněn jednoduchým blokem označeným "Hmotnost (m)", který je spojen s jednoduchou pružinou označenou "Tuhost (k)". — hmotnostně pružinový model

Vzpomínám si, jak jsem spolupracoval s výrobcem automobilových dílů v Michiganu, který nechápal, proč jeho válce bez vodicích tyčí selhávají. Modelováním jejich systému jako jednoduchého uspořádání hmoty a pružiny jsme zjistili, že montážní konzoly fungují jako nechtěné pružiny a vytvářejí rezonanční stav.

Převod reálných systémů na modely s hromadnou pružinou

Chcete-li tento přístup uplatnit na své zařízení:

Identifikace klíčových hmotností: Určete, které složky mají významnou váhu
Vyhledejte pružinové prvky: Najděte komponenty, které ukládají a uvolňují energii (skutečné pružiny, pružné držáky atd.).
Připojení k mapě: Zdokumentujte interakci hmot a pružin
Zjednodušit: Kombinujte podobné prvky, abyste vytvořili zvládnutelný model.

Typy systémů s hromadným odpružením

Typ systému	Popis	Běžné aplikace
Jednotlivé DOF	Jedna hmota s jednou pružinou	Jednoduché pneumatické válce
Multi-DOF	Více hmotností s více pružinami	Složité strojní zařízení s více součástmi
Kontinuální	Nekonečné DOF (vyžaduje jinou analýzu)	Nosníky, desky a skořepiny

Úvahy o pokročilém modelování

I když je základní model s hmotností pružiny cenný, několik vylepšení jej činí realističtějším:

Přidání tlumičů: V reálných systémech vždy dochází k rozptylu energie
Zohlednění nelinearit: Pružiny ne vždy následují Hookův zákon⁴ dokonale
Zohlednění nucených vibrací: Vnější síly mění chování systému
Včetně vazebních efektů: Pohyb v jednom směru může ovlivnit ostatní směry

Optimalizace tlumicího poměru: Jaké experimenty přinášejí nejlepší výsledky?

Tlumení je nejlepší obranou proti problémům s rezonancí. Nalezení optimálního poměru tlumení pomocí experimentů může výrazně zlepšit výkon a spolehlivost systému.

Tlumicí poměr⁵ optimalizační experimenty zahrnují systematické testování různých konfigurací tlumení s cílem najít ideální rovnováhu mezi regulací vibrací a odezvou systému. Optimální poměr tlumení se obvykle pohybuje mezi 0,2 a 0,7 a poskytuje dostatečné potlačení vibrací bez nadměrných energetických ztrát.

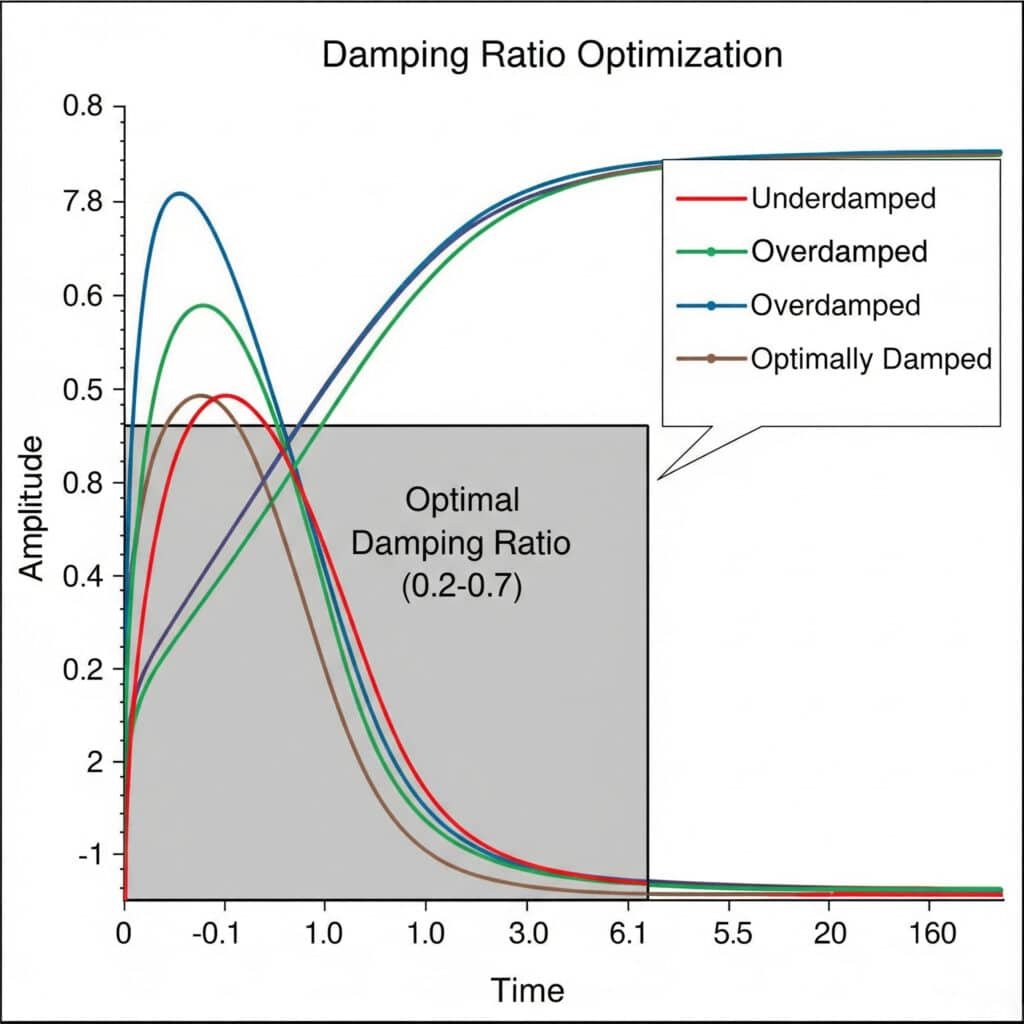
Graf znázorňující optimalizaci tlumicího poměru pomocí grafu závislosti "amplitudy" systému na "čase". Zobrazuje tři různé křivky odezvy: křivku "nedostatečně tlumeného" systému, který výrazně kmitá, křivku "přetlumeného" systému, který se velmi pomalu vrací k nule bez kmitání, a křivku "optimálně tlumeného" systému, který se rychle ustálí s minimálním překmitem. Tato ideální odezva je zvýrazněna stínovanou oblastí označenou jako "Optimální poměr tlumení (0,2-0,7)". — optimalizace tlumicího poměru

Minulý měsíc jsem pomohl jednomu francouzskému výrobci potravinářských zařízení vyřešit přetrvávající problémy s vibracemi jeho magnetických válců bez tyčí. Sérií experimentů s poměrem tlumení jsme zjistili, že jejich původní konstrukce měla poměr tlumení pouze 0,05 - příliš nízký na to, aby zabránil problémům s rezonancí.

Experimentální uspořádání pro testování tlumicího poměru

Provádět experimenty pro optimalizaci účinného tlumení:

Základní měření: Záznam odezvy systému bez dodatečného tlumení
Inkrementální testování: Přidávání tlumicích prvků v řízených krocích
Měření odezvy: Měření amplitudy, doby ustálení a frekvenční odezvy
Analýza dat: Vypočítejte poměr tlumení pro každou konfiguraci
Ověřování: Ověření výkonu za skutečných provozních podmínek

Srovnání technologií tlumení

Technologie tlumení	Výhody	Omezení	Typické aplikace
Viskózní tlumiče	Předvídatelný výkon, teplotně stabilní	Vyžadují údržbu, možné úniky	Těžké stroje, přesná zařízení
Třecí tlumiče	Jednoduchý design, úsporný	Opotřebení v čase, nelineární chování	Konstrukční podpěry, základní strojní zařízení
Tlumení materiálu	Žádné pohyblivé části, kompaktní	Omezený rozsah nastavení	Přesné přístroje, izolace vibrací
Aktivní tlumení	Přizpůsobivost měnícím se podmínkám	Složité, vyžaduje výkon	Kritické aplikace, zařízení s proměnlivými otáčkami

Optimalizace tlumení pro různé provozní podmínky

Ideální poměr tlumení není univerzální - závisí na konkrétní aplikaci:

Vysokorychlostní operace: Nižší poměry tlumení (0,1-0,3) zachovávají rychlost odezvy.
Přesné aplikace: Vyšší poměry tlumení (0,5-0,7) zajišťují stabilitu.
Systémy s proměnným zatížením: Může být nutné adaptivní tlumení
Prostředí citlivá na teplotu: Zvažte tlumicí materiály se stabilními vlastnostmi

Případová studie: Optimalizace tlumení válce bez tyčí

Při optimalizaci dvojčinného válce bez tyče pro balicí stroj jsme testovali pět různých konfigurací tlumení:

Standardní koncové polštáře: Tlumicí poměr = 0,12
Rozšířené polštáře: Tlumicí poměr = 0,25
Vnější tlumiče nárazů: Tlumicí poměr = 0,41
Kompozitní montážní držáky: Tlumicí poměr = 0,38
Kombinovaný přístup (3+4): Tlumicí poměr = 0,53

Kombinovaný přístup poskytl nejlepší výkon, protože snížil amplitudu vibrací o 78% při zachování přijatelné doby odezvy.

Závěr

Pochopení rezonance vibrací prostřednictvím výpočtů vlastní frekvence, modelování hmotných pružin a optimalizace tlumicího poměru je zásadní pro předcházení poruchám zařízení. Uplatněním těchto principů můžete prodloužit životnost strojů, zkrátit prostoje a zlepšit celkovou výkonnost systému.

Časté dotazy o vibrační rezonanci

Co je vibrační rezonance v průmyslových zařízeních?

K vibrační rezonanci dochází, když vnější síla odpovídá vlastní frekvenci systému, což způsobuje zesílené kmitání. V průmyslových zařízeních může tento jev vést k nadměrnému pohybu, únavě součástí a katastrofickým poruchám, pokud není správně řízen.

Jak zjistím, zda můj systém rezonuje?

Hledejte příznaky, jako je nevysvětlitelné zvýšení hluku, viditelné vibrace při určitých rychlostech, předčasné selhání součástí a zhoršení výkonu, ke kterému dochází při stejných provozních bodech. Nástroje pro analýzu vibrací mohou potvrdit rezonanční podmínky.

Jaký je rozdíl mezi nucenými vibracemi a rezonancí?

K vynuceným vibracím dochází vždy, když na systém působí vnější síla, zatímco rezonance je specifický stav, kdy se frekvence vynucené síly shoduje s vlastní frekvencí systému, což vede k zesílené odezvě. Všechny rezonance zahrnují vynucené vibrace, ale ne všechny vynucené vibrace způsobují rezonanci.

Jak ovlivňuje konstrukce pneumatického válce bez tyčí jeho vibrační vlastnosti?

Konstrukce pneumatických válců bez tyčí - s jejich pohyblivým vozíkem, vnitřním těsnicím systémem a vodicími mechanismy - vytváří jedinečné problémy s vibracemi. Prodloužený profil působí jako nosník, který se může ohýbat, hmotnost vozíku vytváří setrvačné síly a těsnicí pásy mohou způsobovat proměnlivé tření.

Jaké jednoduché úpravy mohou snížit rezonanci stávajícího zařízení?

U stávajícího zařízení, které má problémy s rezonancí, zvažte přidání hmotnosti, aby se změnila vlastní frekvence, instalaci externích tlumičů nebo tlumičů nárazů, úpravu způsobů montáže tak, aby zahrnovala izolaci vibrací, nebo úpravu provozních rychlostí, aby se zabránilo rezonančním frekvencím.

Poskytuje základní vysvětlení mechanické rezonance, často s názornými příklady, a ukazuje, jak může malá periodická síla vyvolat v systému oscilace o velké amplitudě. ↩
Nabízí podrobný pohled na fyziku vlastní frekvence, tedy specifické frekvence, při které má systém tendenci kmitat, pokud nepůsobí žádná hnací nebo tlumicí síla. ↩
Vysvětluje principy modelu hmoty a pružiny, který je základní idealizací ve fyzice a inženýrství a používá se k analýze složitých systémů, které vykazují jednoduchý harmonický pohyb. ↩
Podrobnosti Hookův zákon, fyzikální princip, který říká, že síla potřebná k prodloužení nebo stlačení pružiny o určitou vzdálenost je přímo úměrná této vzdálenosti. ↩
Popisuje míru tlumení, bezrozměrnou veličinu, která určuje, jak se kmitání v systému po poruše rozplyne, což je rozhodující pro řízení rezonance. ↩

Dobrý den, jsem Chuck, starší odborník s 15 lety zkušeností v oboru pneumatiky. Ve společnosti Bepto Pneumatic se zaměřuji na poskytování vysoce kvalitních pneumatických řešení na míru našim klientům. Mé odborné znalosti zahrnují průmyslovou automatizaci, návrh a integraci pneumatických systémů, jakož i aplikaci a optimalizaci klíčových komponent. Máte-li jakékoli dotazy nebo chcete-li prodiskutovat potřeby vašeho projektu, neváhejte mě kontaktovat na adrese chuck@bepto.com.