Výrobní prostoje stojí společnosti miliony ročně. Pneumatické válce pohánějí 80% průmyslových automatizačních systémů. Přesto mnoho inženýrů plně nerozumí fyzikálním zákonitostem, díky nimž jsou tyto systémy tak spolehlivé a účinné.
Teorie pneumatických válců je založena na Pascalově zákonu, podle kterého tlak stlačeného vzduchu působí v uzavřené komoře ve všech směrech stejně a díky rozdílu tlaků mění pneumatickou energii na mechanický lineární nebo rotační pohyb.
Před dvěma lety jsem spolupracoval s britským inženýrem Jamesem Thompsonem z Manchesteru, jehož výrobní linka neustále selhávala. Jeho tým nechápal, proč jejich pneumatický systém přerušovaně ztrácí výkon. Po vysvětlení základní teorie jsme identifikovali problémy s poklesem tlaku, které jeho společnosti ušetřily 200 000 liber za ztracenou výrobu.
Obsah
- Jaké jsou základní fyzikální principy pneumatických válců?
- Jak tlakové rozdíly vytvářejí pohyb v pneumatických systémech?
- Jaké jsou klíčové komponenty, které zajišťují fungování pneumatické teorie?
- Jak se tyto principy uplatňují u různých typů pneumatických válců?
- Jaké faktory ovlivňují teorii výkonu pneumatických válců?
- Jak se pneumatické systémy liší od hydraulických a elektrických?
- Závěr
- Časté dotazy k teorii pneumatických válců
Jaké jsou základní fyzikální principy pneumatických válců?
Pneumatické válce fungují na základních fyzikálních principech, které pohánějí průmyslovou automatizaci již více než sto let. Pochopení těchto základů pomáhá inženýrům navrhovat lepší systémy a efektivně řešit problémy.
Pneumatické válce pracují na základě Pascalova zákona, Boyleova zákona a Newtonovy pohybové zákony1, přeměňující energii stlačeného vzduchu na mechanickou sílu prostřednictvím tlakových rozdílů na povrchu pístu.
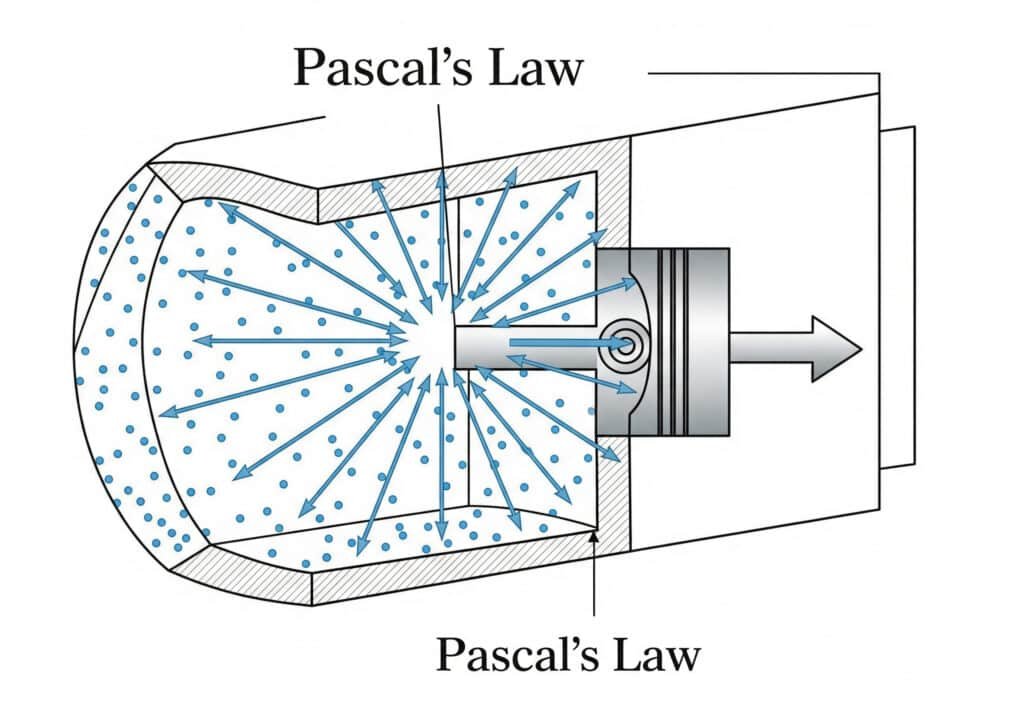
Aplikace Pascalova zákona
Pascalův zákon říká, že tlak působící na uzavřenou kapalinu se přenáší ve všech směrech stejně. V pneumatických válcích to znamená, že tlak stlačeného vzduchu působí rovnoměrně po celé ploše pístu.
Základní rovnice síly je: Síla = tlak × plocha
Pro válec o průměru 4 palce při tlaku 100 PSI:
- Plocha pístu = π × (2)² = 12,57 palce čtverečního
- Výstupní síla = 100 PSI × 12,57 = 1 257 liber
Boyleův zákon a stlačování vzduchu
Boyleův zákon vysvětluje, jak se mění objem vzduchu s tlakem při konstantní teplotě. Tímto principem se řídí, jak stlačený vzduch ukládá energii a jak ji uvolňuje při provozu válce.
Při stlačení vzduchu z atmosférického tlaku (14,7 PSI) na 114,7 PSI (absolutní tlak) se jeho objem zmenší přibližně o 87%. V tomto stlačeném vzduchu je uložena potenciální energie, která se při roztahování válce mění na energii kinetickou.
Newtonovy zákony v pneumatickém pohybu
Druhý Newtonův zákon (F = ma) určuje zrychlení a rychlost válce. Vyšší tlakové rozdíly vytvářejí větší síly, což vede k rychlejšímu zrychlení, dokud tření a odpor zatížení nevyváží hnací sílu.
Klíčové fyzikální vztahy:
| Právo | Aplikace | Vzorec | Dopad na výkon |
|---|---|---|---|
| Pascalův zákon | Generování síly | F = P × A | Určuje maximální sílu |
| Boyleův zákon | Stlačování vzduchu | P₁V₁ = P₂V₂ | Ovlivňuje skladování energie |
| Newtonova 2. | Dynamika pohybu | F = ma | Řízení rychlosti/zrychlení |
| Zachování energie | Účinnost | Ein = Eout + ztráty | Určuje účinnost systému |
Jak tlakové rozdíly vytvářejí pohyb v pneumatických systémech?
Tlakové rozdíly jsou hnací silou veškerého pohybu pneumatických válců. Čím větší je tlakový rozdíl na pístu, tím větší sílu a rychlost válec vytváří.
K pohybu dochází, když stlačený vzduch vstupuje do jedné komory válce, zatímco opačná komora je odvětrávána do atmosféry, čímž vzniká tlakový rozdíl, který pohání pohyb pístu podél otvoru válce.
Teorie jednočinného válce
Jednočinné tlakové lahve používají stlačený vzduch pouze v jednom směru. Pružina nebo gravitace vrací píst do původní polohy, když se tlak vzduchu uvolní.
Při výpočtu efektivní síly je třeba zohlednit odpor pružiny:
Čistá síla = (tlak × plocha) - síla pružiny - tření
Síla pružiny se obvykle pohybuje v rozmezí 10-30% maximální síly válce, což snižuje celkový výkon, ale zajišťuje spolehlivý zpětný pohyb.
Teorie dvojčinného válce
Dvojčinné válce používají stlačený vzduch pro vysouvání i zasouvání. Tato konstrukce zajišťuje maximální sílu v obou směrech a přesné ovládání polohy pístu.
Výpočty síly pro dvojčinné válce:
Prodlužovací síla: F = P × (plná plocha pístu)
Síla zatažení: F = P × (plná plocha pístu - plocha tyče)
Zmenšení plochy tyče znamená, že síla při vtahování je vždy menší než síla při vysouvání. Pro 4palcový válec s 1palcovou tyčí:
- Oblast rozšíření: 12,57 palce čtverečního
- Oblast stažení: 12,57 - 0,785 = 11,785 palce čtverečního
- Rozdíl sil: přibližně o 6% méně při zatahování
Teorie tlakové ztráty
Poklesy tlaku2 se vyskytují v pneumatických systémech v důsledku tření, šroubení a omezení ventilů. Tyto ztráty přímo snižují výkon válce a je třeba je zohlednit při návrhu systému.
Běžné zdroje poklesu tlaku:
- Vzduchové linky: 1-3 PSI na 100 stop
- Kování: 0,5-2 PSI každá
- Ventily: 2-8 PSI v závislosti na provedení
- Filtry: 1-5 PSI, když je čistý
Jaké jsou klíčové komponenty, které zajišťují fungování pneumatické teorie?
Teorie pneumatických válců se opírá o precizně navržené komponenty, které vzájemně spolupracují. Každá součást plní specifickou funkci při přeměně energie stlačeného vzduchu na mechanický pohyb.
Mezi základní součásti patří válec, píst, tyč, těsnění a koncové uzávěry, které jsou navrženy tak, aby zadržovaly tlak, vedly pohyb a účinně přenášely sílu.
Konstrukce válců
Hlaveň válce musí odolávat vnitřnímu tlaku při zachování přesných rozměrů otvoru. Většina průmyslových lahví používá bezešvé ocelové nebo hliníkové trubky s broušené vnitřní povrchy3.
Specifikace hlavně:
| Materiál | Tlakové hodnocení | Povrchová úprava | Typické aplikace |
|---|---|---|---|
| Hliník | Až 250 PSI | 16-32 Ra | Lehké, potravinářské |
| Ocel | Až 500 PSI | 8-16 Ra | Vysokotlaký provoz při vysokém zatížení |
| Nerezová ocel | Až 300 PSI | 8-32 Ra | Korozivní prostředí |
Teorie konstrukce pístu
Písty přenášejí tlakovou sílu na tyč a zároveň utěsňují obě vzduchové komory. Konstrukce pístu ovlivňuje účinnost válce, rychlost a životnost.
Moderní písty používají více těsnicích prvků:
- Primární těsnění: Zabraňuje úniku vzduchu mezi komorami.
- Nosit prsteny: Vedení pohybu pístu a zabránění kontaktu s kovem
- Sekundární těsnění: Záložní těsnění pro kritické aplikace
Teorie těsnicího systému
Těsnění mají zásadní význam pro udržení tlakových rozdílů. Selhání těsnění je nejčastější příčinou problémů s pneumatickými válci v průmyslových aplikacích.
Faktory výkonu těsnění:
- Výběr materiálu: Musí být odolný proti pronikání vzduchu a opotřebení
- Groove Design: Správné rozměry zabraňují vytlačování těsnění
- Povrchová úprava: Hladký povrch snižuje opotřebení těsnění
- Provozní tlak: Vyšší tlaky vyžadují speciální konstrukce těsnění
Jak se tyto principy uplatňují u různých typů pneumatických válců?
Různé konstrukce pneumatických válců používají stejnou základní teorii, ale optimalizují výkon pro konkrétní aplikace. Pochopení těchto variant pomáhá konstruktérům při výběru vhodných řešení.
Různé typy válců modifikují základní pneumatickou teorii prostřednictvím specializovaných konstrukcí, jako jsou válce bez tyčí, rotační aktuátory a vícepolohové válce, přičemž každý z nich optimalizuje sílu, rychlost nebo pohybové charakteristiky.
Pneumatický válec bez tyče
Válce bez tyčí4 Teorie
eliminují tradiční pístní tyč, což umožňuje delší zdvihy v kompaktních prostorech. K přenosu pohybu mimo válec používají magnetickou spojku nebo kabelové systémy.
Konstrukce magnetické spojky:
Vnitřní píst obsahuje permanentní magnety, které se přes stěnu válce spojují s vnějším vozíkem. Tato konstrukce zabraňuje úniku vzduchu a zároveň přenáší plnou sílu pístu.
Účinnost přenosu síly: 95-98% se správnou magnetickou vazbou
Maximální zdvih: Omezeno pouze délkou válce, a to až na více než 20 stop.
Schopnost rychlosti: Až 60 palců za sekundu v závislosti na zatížení
Teorie rotačního pohonu
Rotační pneumatické pohony5 převádějí lineární pohyb pístu na rotační pohyb pomocí převodových mechanismů nebo lopatkových konstrukcí. Tyto systémy využívají pneumatickou teorii k vytvoření přesného úhlového polohování.
Rotační pohony lopatkového typu:
Stlačený vzduch působí na lopatky ve válcové komoře a vytváří točivý moment. Výpočet točivého momentu je následující: Točivý moment = tlak × plocha lopatek × poloměr
Teorie vícepolohových válců
Vícepolohové válce využívají více vzduchových komor k vytvoření mezipoloh zastavení. Tato konstrukce využívá pneumatickou teorii se složitými ventilovými systémy pro přesné řízení polohy.
Mezi běžné konfigurace patří:
- Třípolohový: Dva meziplyny a plné vysunutí
- Pět poloh: Čtyři mezizastávky a plný zdvih
- Proměnlivá poloha: Nekonečné polohování se servoventilem
Jaké faktory ovlivňují teorii výkonu pneumatických válců?
Na to, jak dobře se teorie pneumatiky projeví v reálném provozu, má vliv více faktorů. Pochopení těchto proměnných pomáhá inženýrům optimalizovat návrh systému a řešit problémy.
Mezi klíčové faktory výkonu patří kvalita vzduchu, kolísání teploty, charakteristiky zatížení, způsoby montáže a stabilita tlaku v systému, které mohou významně ovlivnit teoretický výkon.
Vliv kvality ovzduší na teorii
Kvalita stlačeného vzduchu přímo ovlivňuje výkon a životnost pneumatických válců. Znečištěný vzduch způsobuje opotřebení těsnění, korozi a snížení účinnosti.
Normy kvality ovzduší:
| Kontaminant | Maximální úroveň | Dopad na výkon |
|---|---|---|
| Vlhkost | rosný bod -40°F | Zabraňuje korozi a zamrzání |
| Olej | 1 mg/m³ | Snižuje degradaci těsnění |
| Částice | 5 mikronů | Zabraňuje opotřebení a přilepení |
Vliv teploty na pneumatickou teorii
Změny teploty ovlivňují hustotu vzduchu, tlak a rozměry součástí. Tyto změny mohou významně ovlivnit výkon válce v extrémních podmínkách.
Vzorec pro kompenzaci teploty: P₂ = P₁ × (T₂/T₁)
Při každém zvýšení teploty o 100 °F se tlak vzduchu zvýší přibližně o 20%, pokud objem zůstane konstantní. To ovlivňuje výkon síly a musí se zohlednit při návrhu systému.
Charakteristiky zatížení a dynamické síly
Statické a dynamické zatížení ovlivňuje výkonnost válce odlišně. Dynamické zatížení vytváří dodatečné síly, které je třeba překonat během zrychlení a zpomalení.
Dynamická silová analýza:
- Síla zrychlení: F = ma (hmotnost × zrychlení)
- Třecí síla: Obvykle 10-20% aplikovaného zatížení
- Setrvačné síly: Významné při vysokých rychlostech nebo při velkém zatížení.
Nedávno jsem pomáhal jednomu americkému výrobci jménem Robert Chen v Detroitu optimalizovat jeho pneumatický systém pro těžké automobilové díly. Analýzou dynamických sil jsme zkrátili dobu cyklu o 30% a zároveň zlepšili přesnost polohování.
Stabilita tlaku v systému
Kolísání tlaku ovlivňuje konzistenci výkonu lahve. Správná úprava a skladování vzduchu pomáhají udržovat stabilní provozní podmínky.
Požadavky na stabilitu tlaku:
- Změny tlaku: Pro konzistentní výkon by neměl překročit ±5%.
- Velikost nádrže přijímače: 5-10 galonů na spotřebu vzduchu CFM
- Regulace tlaku: V rozmezí ±1 PSI pro přesné aplikace
Jak se pneumatické systémy liší od hydraulických a elektrických?
Pneumatická teorie nabízí ve srovnání s jinými způsoby přenosu energie výrazné výhody a omezení. Pochopení těchto rozdílů pomáhá konstruktérům vybrat optimální řešení pro konkrétní aplikace.
Pneumatické systémy poskytují rychlou odezvu, jednoduché ovládání a čistý provoz, ale v porovnání s hydraulickými a elektrickými alternativami mají nižší hustotu síly a méně přesné polohování.
Teoretické srovnání výkonu
| Charakteristika | Pneumatické | Hydraulika | Elektrický |
|---|---|---|---|
| Hustota výkonu | 15-25 HP/lb | 50-100 HP/lb | 5-15 HP/lb |
| Doba odezvy | 10-50 ms | 5-20 ms | 50-200 ms |
| Přesnost polohování | ±0,1 palce | ±0,01 palce | ±0,001 palce |
| Provozní tlak | 80-150 PSI | 1000-5000 PSI | N/A (napětí) |
| Účinnost | 20-30% | 40-60% | 80-95% |
| Frekvence údržby | Nízká | Vysoká | Střední |
Teorie účinnosti přeměny energie
Pneumatické systémy mají přirozená omezení účinnosti způsobená ztrátami při stlačování vzduchu a tvorbou tepla. Teoretická maximální účinnost je přibližně 37% pro izotermickou kompresi, ale reálné systémy dosahují 20-30%.
Zdroje ztrát energie:
- Kompresní teplo: 60-70% vstupní energie
- Tlakové kapky: 5-15% systémového tlaku
- Únik: 2-10% spotřeby vzduchu
- Škrtící ztráty: Proměnná v závislosti na způsobu ovládání
Rozdíly v teorii řízení
Teorie pneumatického řízení se od hydraulických a elektrických systémů výrazně liší díky stlačitelnosti vzduchu. Tato vlastnost poskytuje přirozené tlumení, ale ztěžuje přesné polohování.
Kontrolní charakteristiky:
- Dodržování přírodních předpisů: Stlačitelnost vzduchu zajišťuje tlumení nárazů
- Řízení rychlosti: Dosaženo spíše omezením průtoku než změnou tlaku.
- Kontrola síly: Obtížné vzhledem ke složitosti vztahu tlak/průtok
- Zpětná vazba k poloze: Vyžaduje externí senzory pro přesné ovládání
Závěr
Teorie pneumatických válců spojuje základní fyzikální principy s praktickým inženýrstvím a vytváří spolehlivé a účinné systémy přenosu energie pro nespočet průmyslových aplikací po celém světě.
Časté dotazy k teorii pneumatických válců
Jaká je základní teorie pneumatických válců?
Pneumatické válce fungují na základě Pascalova zákona, kdy tlak stlačeného vzduchu působí v uzavřené komoře ve všech směrech stejně a vytváří sílu, když tlakové rozdíly pohybují písty v otvorech válce.
Jak se vypočítá síla pneumatického válce?
Síla se rovná tlaku krát plocha pístu (F = P × A). Válec o průměru 4 palce při tlaku 100 PSI vytváří přibližně 1257 liber síly, po odečtení tření a dalších ztrát.
Proč jsou pneumatické válce méně účinné než hydraulické systémy?
Stlačitelnost vzduchu způsobuje energetické ztráty během kompresních a expanzních cyklů, což omezuje účinnost pneumatických systémů na 20-30% ve srovnání s hydraulickými systémy dosahujícími účinnosti 40-60%.
Jaké faktory ovlivňují rychlost pneumatických válců?
Rychlost závisí na průtoku vzduchu, objemu válce, hmotnosti zátěže a tlakovém rozdílu. Vyšší průtoky a tlaky zvyšují rychlost, zatímco těžší zátěž zrychlení snižuje.
Jak ovlivňuje teplota výkon pneumatických válců?
Změny teploty ovlivňují hustotu a tlak vzduchu. Každé zvýšení teploty o 100 °F zvýší tlak vzduchu přibližně o 20%, což má přímý vliv na výkon a výkonnost systému.
Jaký je rozdíl mezi jednočinným a dvojčinným válcem?
Jednočinné válce používají stlačený vzduch pouze v jednom směru s vratnou pružinou, zatímco dvojčinné válce používají tlak vzduchu pro vysouvání i zasouvání.
-
Poskytuje podrobný přehled tří Newtonových pohybových zákonů, které jsou základními principy klasické mechaniky popisujícími vztah mezi tělesem a silami, které na něj působí, a jeho pohyb v reakci na tyto síly. ↩
-
Podrobně popisuje příčiny poklesu tlaku v pneumatických systémech, včetně tření v potrubí a ztrát způsobených armaturami, ventily a filtry, a vysvětluje, jak snižují dostupnou energii v místě použití. ↩
-
Vysvětluje proces honování, brusný obráběcí proces, při kterém se na obrobku vytváří přesný povrch drhnutím brusným kamenem, často používaným k vytvoření specifického křížového vzoru na otvorech válců pro zadržování oleje. ↩
-
Popisuje různé konstrukce beztaktních válců, jako jsou magneticky spřažené a mechanicky spřažené (pásové) typy, a vysvětluje jejich výhody, jako je zajištění dlouhých zdvihů v kompaktním prostoru. ↩
-
Vysvětluje různé mechanismy, jako je ozubené kolo nebo lamelové provedení, které pneumatické rotační aktuátory používají k přeměně lineární síly stlačeného vzduchu na rotační pohyb nebo točivý moment. ↩





