Jaké jsou základní rovnice pneumatického přenosu, které by měl znát každý inženýr?

Třípanelová technická infografika zobrazující základní pneumatické rovnice. První panel znázorňuje zákon ideálního plynu (PV = nRT) pomocí schématu uzavřené nádrže na plyn. Druhý panel vysvětluje rovnici síly (F = P × A) pomocí schématu pístu. Třetí panel ukazuje vztah pro průtok (Q = v × A) pomocí schématu vzduchu pohybujícího se potrubím, přičemž každá proměnná ve vzorcích je jasně spojena s odpovídajícím vizuálním prvkem. — zákon ideálního plynu

Neustále se potýkáte s výpočty pneumatických systémů? Mnoho inženýrů se potýká se stejným problémem při navrhování nebo řešení problémů s pneumatickými systémy. Dobrou zprávou je, že zvládnutí několika klíčových rovnic může vyřešit většinu vašich pneumatických problémů.

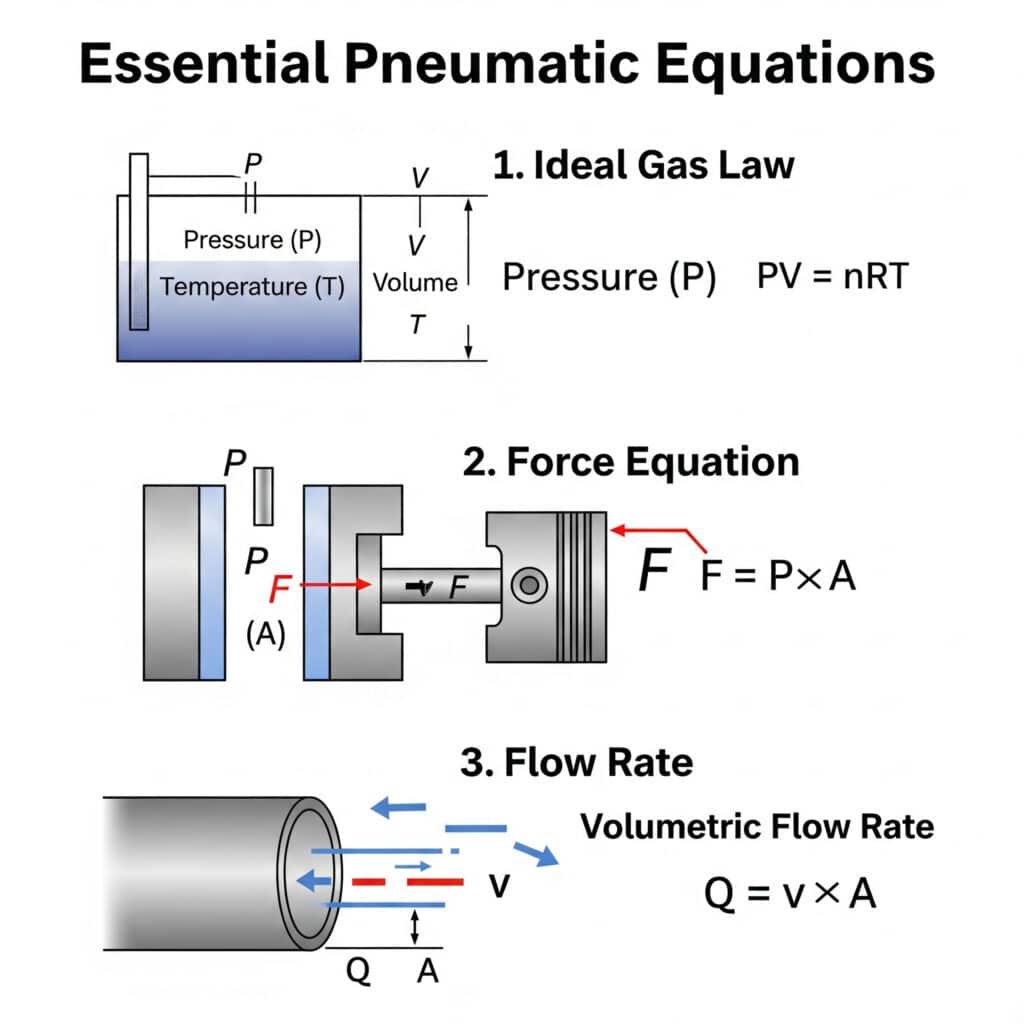
Mezi základní rovnice pneumatického převodu, které by měl znát každý inženýr, patří. zákon ideálního plynu (PV = nRT)¹, rovnice síly (F = P × A) a vztah pro průtok (Q = v × A). Pochopení těchto základních principů umožňuje přesný návrh systému a řešení problémů.

Ve společnosti Bepto jsem strávil více než 15 let prací s pneumatickými systémy a na vlastní kůži jsem se přesvědčil, že pochopení těchto základních rovnic může ušetřit tisíce dolarů za prostoje a zabránit nákladným konstrukčním chybám.

Obsah

Odvození plynové rovnice: Proč je PV = nRT důležité v pneumatických systémech?
Jak souvisí síla, tlak a plocha v pneumatických válcích?
Jaký je vztah mezi průtokem a rychlostí v pneumatických systémech?
Závěr
Často kladené otázky o rovnicích pneumatického přenosu

Odvození plynové rovnice: Proč je PV = nRT důležité v pneumatických systémech?

Při navrhování pneumatických systémů je zásadní pochopit, jak se plyny chovají za různých podmínek. Tyto znalosti mohou znamenat rozdíl mezi systémem, který funguje spolehlivě, a systémem, který neočekávaně selže.

Zákon ideálního plynu (PV = nRT) je pro pneumatické systémy zásadní, protože popisuje vzájemné působení tlaku, objemu a teploty. Tento vztah pomáhá konstruktérům předpovídat, jak se bude chovat vzduch v beztlakových válcích a dalších pneumatických komponentách za různých provozních podmínek.

Technické schéma vysvětlující zákon ideálního plynu. Zobrazuje uzavřenou nádobu, která představuje pevný "objem (V)". Měřidlo na nádobě udává "tlak (P)" a štítek udává "teplotu (T)". Výrazně je zobrazen vzorec "PV = nRT", který spojuje pojmy tlak, objem a teplota pro plyn uvnitř nádoby. — Aplikace plynového zákona v pneumatice

Zákon ideálního plynu se může zdát jako teoretický koncept z hodin fyziky, ale má přímé praktické využití v pneumatických systémech. Dovolte mi, abych jej rozvedl do praktičtějších pojmů.

Pochopení proměnných ve vztahu PV = nRT

Proměnná	Význam	Pneumatická aplikace
P	Tlak	Provozní tlak v systému
V	Svazek	Velikost vzduchové komory ve válcích
n	Počet molů	Množství vzduchu v systému
R	Plynová konstanta²	Univerzální konstanta (8,314 J/mol-K)
T	Teplota	Provozní teplota

Jak teplota ovlivňuje výkon pneumatiky

Změny teploty mohou významně ovlivnit výkon pneumatického systému. V loňském roce se na mě obrátil jeden z našich zákazníků v Německu, Hans, kvůli nestálému výkonu jeho systému bez tyčových válců. Ráno systém fungoval perfektně, ale odpoledne ztratil výkon.

Po analýze jeho nastavení jsme zjistili, že systém byl vystaven přímému slunečnímu záření, což způsobilo zvýšení teploty o 15 °C. Pomocí zákona ideálního plynu jsme vypočítali, že tato změna teploty způsobuje změnu tlaku o téměř 5%. Nainstalovali jsme vhodnou izolaci a problém byl okamžitě vyřešen.

Praktické aplikace plynového zákona při navrhování pneumatických zařízení

Při navrhování pneumatických systémů s válce bez tyčí, pomáhá nám zákon plynu:

Výpočet změn tlaku v důsledku kolísání teploty
Stanovení požadavků na objem vzduchových nádrží
Předpovídat změny silového výkonu za různých podmínek
Kompresory dimenzujte vhodně pro danou aplikaci

Jak souvisí síla, tlak a plocha v pneumatických válcích?

Při výběru správného beztlakového válce pro vaši aplikaci je důležité pochopit vztah mezi silou, tlakem a plochou. Díky těmto znalostem získáte potřebný výkon bez zbytečných výdajů.

Na stránkách vztah mezi silou, tlakem a plochou³ v pneumatických válcích je definován vztahem F = P × A, kde F je síla (N), P je tlak (Pa) a A je účinná plocha (m²). Tato rovnice umožňuje konstruktérům vypočítat přesný silový výkon beztlakových válců při různých provozních tlacích.

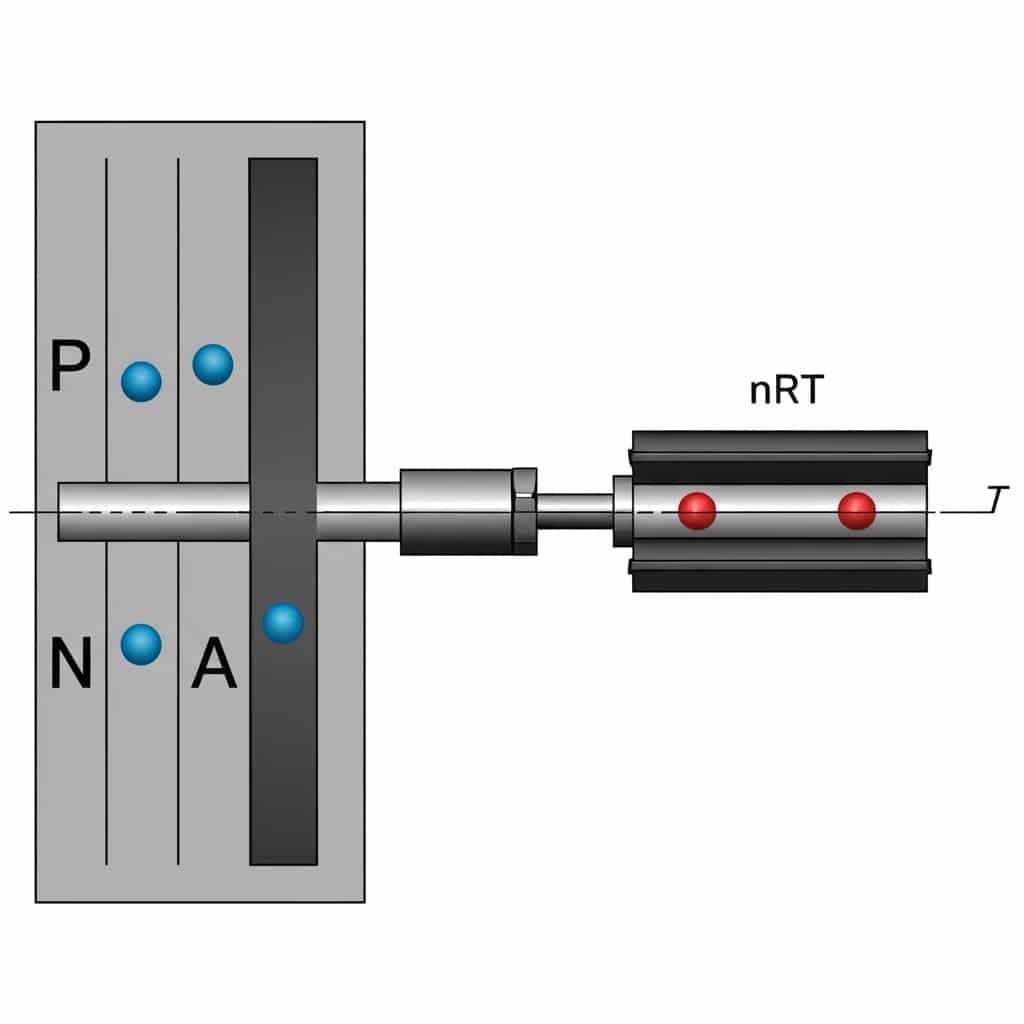
Technické schéma znázorňující výpočet síly v bezprutovém pneumatickém válci. Plocha pístu válce je označena "A" a vnitřní tlak vzduchu je označen "P". Šipka označuje výslednou sílu (F), kterou válec působí. Vpravo je zobrazen vzorec "F = P × A", který jasně ukazuje vztah mezi těmito třemi veličinami. — Výpočet síly v bezprutových válcích

Tato jednoduchá rovnice je základem všech výpočtů pneumatické síly, ale existuje několik praktických úvah, které mnoho inženýrů přehlíží.

Výpočty efektivní plochy pro různé typy lahví

Účinná plocha se liší v závislosti na typu válce:

Typ válce	Výpočet efektivní plochy	Poznámky
Jednočinný	A = πr²	Celá plocha otvoru
Dvojčinný (prodlužovací)	A = πr²	Celá plocha otvoru
Dvojčinný (zatahovací)	A = π(r² - r'²)	r' je poloměr tyče
Válec bez tyčí	A = πr²	Konzistentní v obou směrech

Faktory efektivity síly v reálném světě

V praxi je skutečný silový výkon ovlivněn:

Ztráty třením: Obvykle 3-20% v závislosti na provedení těsnění.
Poklesy tlaku: Může snížit účinný tlak o 5-10%
Dynamické efekty: Akcelerační síly mohou snížit dostupnou sílu

Vzpomínám si na spolupráci se Sarah, strojní inženýrkou z obalové společnosti ve Velké Británii. Navrhovala nový stroj a spočítala, že k dosažení požadované síly potřebuje válec bez tyče s otvorem 63 mm. Nepočítala však se ztrátami třením.

Doporučili jsme zvětšit válec na 80 mm, což poskytlo dostatečnou dodatečnou sílu k překonání tření při zachování požadovaného výkonu. Tato jednoduchá úprava ji zachránila před nákladným přepracováním po instalaci.

Porovnání teoretického a skutečného výkonu síly

Při výběru válců bez tyčí vždy doporučuji:

Vypočítejte teoretickou sílu pomocí F = P × A
Pro většinu aplikací použijte bezpečnostní faktor 25%.
Ověřte výpočty podle skutečných údajů o výkonu od výrobce.
V případě potřeby zvažte dynamické podmínky zatížení

Jaký je vztah mezi průtokem a rychlostí v pneumatických systémech?

Průtok a rychlost jsou kritické parametry, které určují rychlost reakce pneumatického systému. Pochopení tohoto vztahu pomáhá předcházet pomalému výkonu a zajišťuje, že váš systém splní požadavky na dobu cyklu.

Vztah mezi průtok (Q) a rychlost (v)⁴ v pneumatických systémech je definován vztahem Q = v × A, kde Q je objemový průtok, v je rychlost proudění vzduchu a A je plocha průřezu průchodu. Tato rovnice je rozhodující pro správné dimenzování vzduchových vedení a ventilů.

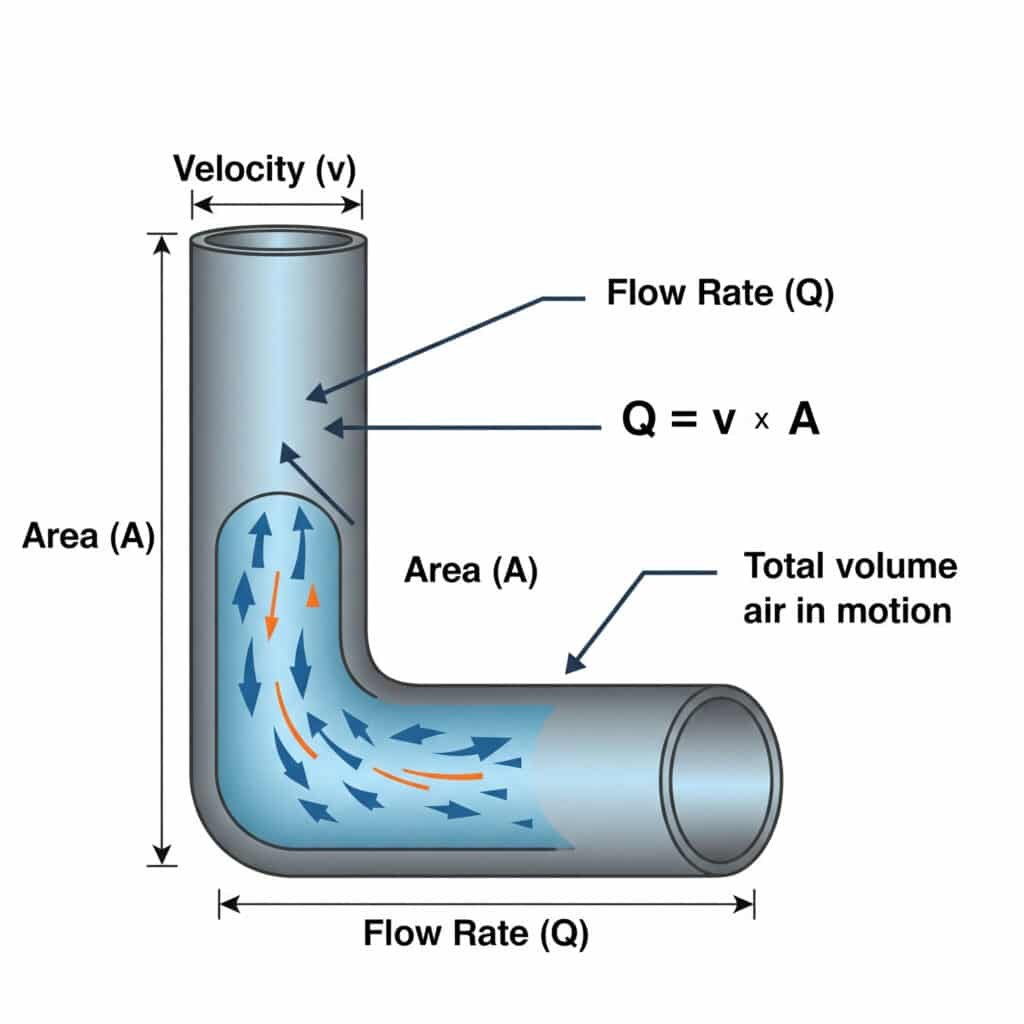
Technický diagram vysvětlující vztah mezi průtokem, rychlostí a plochou. Zobrazuje přímou trubku, kterou proudí vzduch. Rychlost vzduchu je vyznačena šipkou označenou "Velocity (v)". Kruhový otvor potrubí je označen jako "plocha (A)". Výsledný celkový průtok je označen jako "průtok (Q)". Vzorec "Q = v × A" je zobrazen na viditelném místě a šipky spojují každou proměnnou s odpovídajícím prvkem na obrázku. — Vztah mezi průtokem a rychlostí

Mnoho problémů s pneumatickými systémy vzniká v důsledku nesprávného dimenzování komponent pro přívod vzduchu. Podívejme se, jak tato rovnice ovlivňuje skutečný výkon.

Kritické průtoky pro běžné pneumatické součásti

Různé komponenty mají různé požadavky na průtok:

Komponenta	Typický požadavek na průtok	Dopad poddimenzování
Válec bez tyčí (vrtání 25 mm)	15-30 l/min	Pomalý provoz, snížená síla
Válec bez tyčí (vrtání 63 mm)	60-120 l/min	Nekonzistentní pohyb
Směrový regulační ventil	Liší se podle velikosti	Pokles tlaku, pomalá odezva
Jednotka pro přípravu vzduchu	Systém celkem + 30%	Kolísání tlaku

Jak průměr potrubí ovlivňuje výkon systému

Průměr vzduchového potrubí má zásadní vliv na výkon systému:

Pokles tlaku: Zvyšuje se se čtvercem rychlosti
Doba odezvy: Menší čáry znamenají vyšší rychlost, ale větší odpor.
Energetická účinnost: Větší vedení snižují tlakovou ztrátu, ale zvyšují náklady

Výpočet správné velikosti potrubí pro pneumatické systémy

Pro správné dimenzování vzduchového potrubí pro použití beztlakových lahví:

Stanovení požadovaného průtoku na základě velikosti válce a doby cyklu.
Vypočítejte maximální přípustný pokles tlaku (obvykle 0,1 baru nebo méně).
Zvolte průměr vedení, který udržuje rychlost pod 15-20 m/s.
Ověřte průtokovou kapacitu ventilu (Hodnota Cv nebo Kv⁵) odpovídá systémovým požadavkům

Jednou jsem pomáhal zákazníkovi ve Francii, který měl problém s pomalým pohybem válce, přestože měl velký kompresor. Problém nebyl v nedostatečné výrobě vzduchu - jeho 6mm trubky kladly nadměrný odpor. Modernizace na 10mm potrubí problém okamžitě vyřešila a zvýšila rychlost cyklu jeho stroje o 40%.

Závěr

Porozumění těmto třem základním pneumatickým rovnicím - zákonu ideálního plynu, vztahu mezi silou, tlakem a plochou a vztahu mezi rychlostí a průtokem - poskytuje základ pro úspěšný návrh pneumatického systému. Uplatněním těchto principů můžete vybrat správné komponenty beztlakových válců, účinně řešit problémy a optimalizovat výkon systému.

Často kladené otázky o rovnicích pneumatického přenosu

Co je to zákon ideálního plynu a proč je důležitý pro pneumatické systémy?

Zákon ideálního plynu (PV = nRT) popisuje vztah tlaku, objemu, teploty a množství plynu v pneumatickém systému. Je důležitý, protože pomáhá konstruktérům předvídat, jak měnící se podmínky (zejména teplota) ovlivní výkon systému a požadavky na tlak.

Jak vypočítám silový výkon válce bez tyčí?

Výstupní sílu vypočtěte vynásobením tlaku efektivní plochou (F = P × A). U válce bez tyče je efektivní plocha stejná v obou směrech, takže výpočet síly je jednodušší než u běžných válců, které mají různé síly při vysouvání a zasouvání.

Jaký je rozdíl mezi průtokem a rychlostí v pneumatických systémech?

Průtok je objem vzduchu, který projde systémem za jednotku času (obvykle v l/min), zatímco rychlost je rychlost, kterou se vzduch pohybuje průchodem (v m/s). Souvisí spolu podle rovnice Q = v × A, kde A je plocha průřezu průchodu.

Jak teplota ovlivňuje výkon pneumatického systému?

Teplota přímo ovlivňuje tlak podle zákona ideálního plynu. Zvýšení teploty o 10 °C může zvýšit tlak přibližně o 3,5%, pokud objem zůstane konstantní. To může způsobit kolísání tlaku, ovlivnit výkonnost těsnění a změnit silový výkon v beztlakových lahvích.

Jaká je nejčastější příčina poklesu tlaku v pneumatických systémech?

Nejčastějšími příčinami poklesu tlaku jsou poddimenzované vzduchové potrubí, omezující armatury a nedostatečná průtočná kapacita ventilů. Podle rovnice průtoku vyžadují menší průchody vyšší rychlost vzduchu, což exponenciálně zvyšuje odpor a tlakovou ztrátu.

Jak správně dimenzovat vzduchové potrubí pro bezprutovou láhev?

Velikost vzduchového potrubí určete výpočtem požadovaného průtoku na základě objemu válce a doby cyklu a poté zvolte takový průměr potrubí, aby rychlost vzduchu byla nižší než 15-20 m/s a minimalizovala se tak tlaková ztráta. Pro většinu aplikací beztlakových válců poskytují 8-12mm vedení dobrý poměr mezi výkonem a náklady.

Podrobně vysvětluje zákon ideálního plynu, základní stavovou rovnici pro hypotetický ideální plyn, která aproximuje chování mnoha plynů za různých podmínek. ↩
Vysvětlí úlohu a hodnotu univerzální plynové konstanty (R) v zákoně ideálního plynu, která slouží jako fyzikální konstanta spojující stupnice energie se stupnicemi teploty. ↩
Nabízí základní vysvětlení pojmu tlak, který je definován jako síla působící kolmo na povrch objektu na jednotku plochy, na kterou je tato síla rozložena. ↩
Podrobně se seznámí s principem rovnice kontinuity, základním pojmem v dynamice tekutin, který říká, že pro nestlačitelnou tekutinu musí být hmotnostní průtok konstantní od jednoho průřezu potrubí k druhému. ↩
Poskytuje technickou definici průtokového součinitele (Cv) a průtokového faktoru (Kv), což jsou standardizované hodnoty používané k porovnávání průtokových kapacit různých ventilů. ↩

Dobrý den, jsem Chuck, starší odborník s 15 lety zkušeností v oboru pneumatiky. Ve společnosti Bepto Pneumatic se zaměřuji na poskytování vysoce kvalitních pneumatických řešení na míru našim klientům. Mé odborné znalosti zahrnují průmyslovou automatizaci, návrh a integraci pneumatických systémů, jakož i aplikaci a optimalizaci klíčových komponent. Máte-li jakékoli dotazy nebo chcete-li prodiskutovat potřeby vašeho projektu, neváhejte mě kontaktovat na adrese chuck@bepto.com.