
Er du nogensinde gået ind på fabriksgulvet og blevet ramt af den umiskendelige susen fra pneumatiske systemer? Den støj er ikke bare et irritationsmoment - den repræsenterer spildt energi, potentielle problemer med lovgivningen og et advarselstegn på ineffektiv drift.
Akustisk støj i pneumatiske systemer genereres gennem tre primære mekanismer: gasudvidelse under trykaflastning, mekanisk vibration af komponenter og turbulent flow i rør og fittings. Ved at forstå disse mekanismer kan ingeniører implementere målrettede støjreduktionsstrategier, der forbedrer sikkerheden på arbejdspladsen, øger energieffektiviteten og forlænger udstyrets levetid.
I sidste måned besøgte jeg et farmaceutisk produktionsanlæg i New Jersey, hvor overdreven støj fra deres stangløse cylindre gav anledning til lovgivningsmæssige bekymringer. Deres team havde prøvet generiske løsninger uden held. Ved at analysere de specifikke støjgenereringsmekanismer reducerede vi deres systemstøj med 14 dBA - fra at udgøre en risiko for lovgivningen til at overholde den. Lad mig vise dig, hvordan vi gjorde det.
Indholdsfortegnelse
- Lydniveau for gasudvidelse: Hvilken formel forudsiger pneumatisk udstødningsstøj?
- Mekanisk vibrationsspektrum: Hvordan kan frekvensanalyse identificere støjkilder?
- Lyddæmperens indskydningstab: Hvilke beregninger driver effektivt lyddæmperdesign?
- Konklusion
- Ofte stillede spørgsmål om støj fra pneumatiske systemer
Lydniveau for gasudvidelse: Hvilken formel forudsiger pneumatisk udstødningsstøj?
Den pludselige udvidelse af trykluft under ventilbetjening eller cylinderudstødning skaber en af de mest markante støjkilder i pneumatiske systemer. At forstå det matematiske forhold mellem systemparametre og støjoutput er afgørende for en effektiv afhjælpning.
Lydeffektniveauet fra gasudvidelse kan beregnes ved hjælp af formlen: Lw = 10 log₁₀(W/W₀), hvor W er den akustiske effekt i watt, og W₀ er referenceeffekten (10-¹² watt). For pneumatiske systemer kan W estimeres som W = η × m × (c²/2), hvor η er den akustiske effektivitet, m er massestrømningshastigheden, og c er gashastigheden.
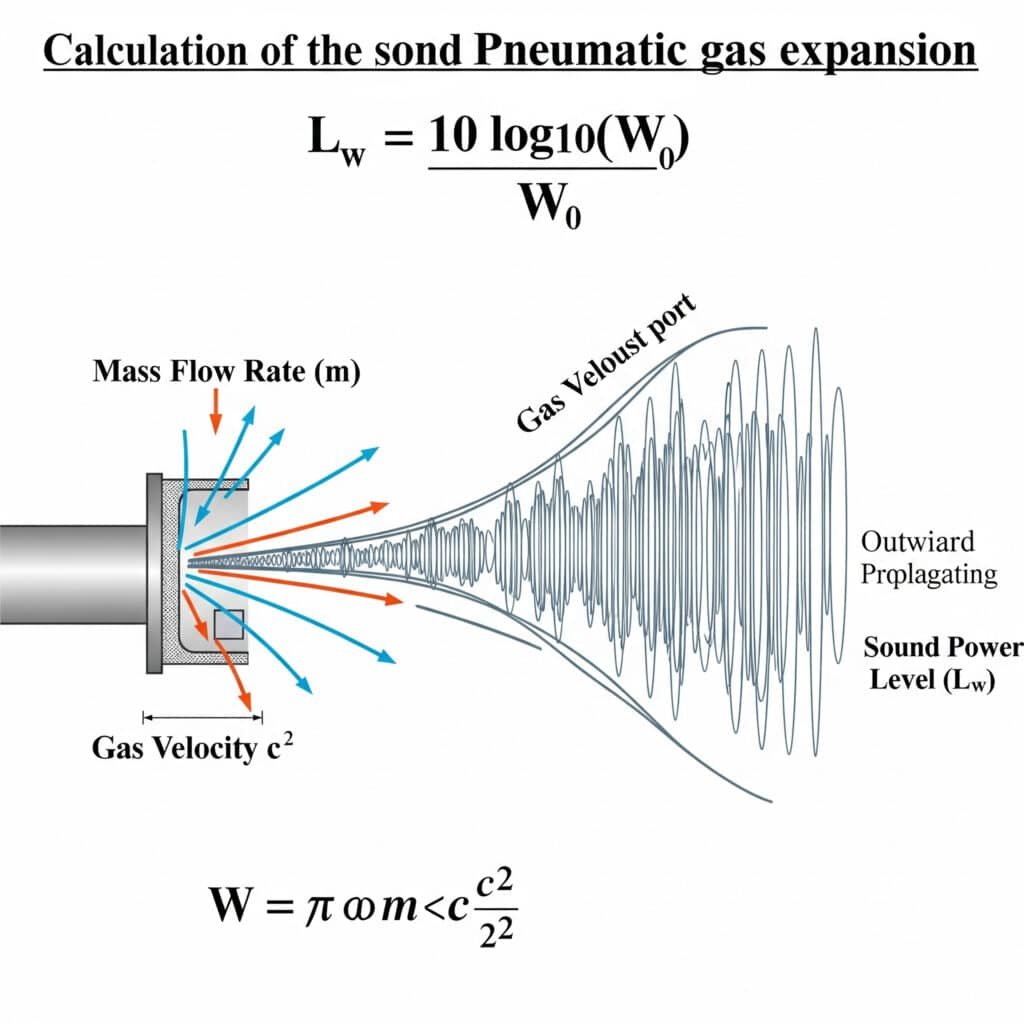
Jeg kan huske, at jeg fejlsøgte på en pakkelinje i Illinois, hvor støjniveauet oversteg 95 dBA - langt over OSHA-grænser1. Vedligeholdelsesteamet havde fokuseret på mekaniske kilder, men vores analyse afslørede, at 70% af støjen kom fra udstødningsportene. Ved at anvende gasudvidelsesformlen fandt vi ud af, at deres driftstryk var 2,2 bar højere end nødvendigt, hvilket skabte for meget udstødningsstøj. Denne enkle trykjustering reducerede støjen med 8 dBA uden at påvirke ydeevnen.
Grundlæggende ligninger for gasekspansionsstøj
Lad os se nærmere på de vigtigste formler til at forudsige ekspansionsstøj:
Beregning af lydeffekt
Den akustiske effekt, der genereres af ekspanderende gas, kan beregnes som:
W = η × m × (c²/2)
Hvor?
- W = Akustisk effekt (watt)
- η = Akustisk effektivitet (typisk 0,001-0,01 for pneumatiske udstødninger)
- m = Massestrømningshastighed (kg/s)
- c = Gashastighed ved udstødningen (m/s)
Lydeffektniveauet i decibel er derefter:
Lw = 10 log₁₀(W/W₀)
Hvor W₀ er referenceeffekten på 10-¹² watt.
Bestemmelse af masseflowhastighed
Massestrømningshastigheden gennem en åbning kan beregnes som:
m = Cd × A × p₁ × √(2γ/(γ-1) × (RT₁) × [(p₂/p₁)^(2/γ) - (p₂/p₁)^((γ+1)/γ)])
Hvor?
- Cd = Udledningskoefficient (typisk 0,6-0,8)
- A = Orifice-areal (m²)
- p₁ = Absolut opstrømstryk (Pa)
- p₂ = Absolut tryk nedstrøms (Pa)
- γ = Specifikt varmeforhold (1,4 for luft)
- R = Gaskonstant for luft (287 J/kg-K)
- T₁ = Opstrøms temperatur (K)
For kvalt flow (almindeligt i pneumatiske udstødninger) forenkles dette til:
m = Cd × A × p₁ × √(γ/(RT₁)) × (2/(γ+1))^((γ+1)/(2(γ-1)))
Faktorer, der påvirker støj fra gasudvidelse
| Faktor | Indvirkning på støjniveauet | Tilgang til afhjælpning |
|---|---|---|
| Driftstryk | 3-4 dBA stigning pr. bar | Reducer systemtrykket til det nødvendige minimum |
| Størrelse på udstødningsport | Mindre porte øger hastigheden og støjen | Brug porte af korrekt størrelse til flowkrav |
| Udstødningstemperatur | Højere temperaturer øger støjen | Tillad afkøling før udvidelse, hvor det er muligt |
| Udvidelsesgrad | Højere forhold skaber mere støj | Udvidelse af scenen gennem flere trin |
| Flowhastighed | Fordobling af flowet øger støjen med ~3 dBA | Brug flere mindre udstødninger i stedet for én stor |
Praktisk eksempel på forudsigelse af støj
For en typisk stangløs cylinder med:
- Driftstryk: 6 bar (600.000 Pa)
- Udstødningsportens diameter: 4 mm (areal = 1,26 × 10-⁵ m²)
- Udledningskoefficient: 0,7
- Akustisk effektivitet: 0,005
Massestrømmen under udstødningen vil være ca:
m = 0,7 × 1,26 × 10-⁵ × 600.000 × 0,0404 = 0,0214 kg/s
Hvis man antager en udstødningshastighed på 343 m/s (sonisk hastighed), vil den akustiske effekt være:
W = 0,005 × 0,0214 × (343²/2) = 6,29 watt
Det resulterende lydeffektniveau:
Lw = 10 log₁₀(6,29/10-¹²) = 128 dB
Dette høje lydeffektniveau forklarer, hvorfor udstødning af trykluft uden lyd er en så betydelig støjkilde i industrielle miljøer.
Mekanisk vibrationsspektrum: Hvordan kan frekvensanalyse identificere støjkilder?
Mekaniske vibrationer i pneumatiske komponenter genererer karakteristiske støjsignaturer, som kan analyseres for at lokalisere specifikke problemer. Frekvensspektrumanalyse er nøglen til at identificere og håndtere disse mekaniske støjkilder.
Mekaniske vibrationer i pneumatiske systemer producerer støj med karakteristiske frekvensspektre, der kan analyseres ved hjælp af Hurtig Fourier-transformation (FFT)2 teknikker. De vigtigste frekvensområder omfatter lavfrekvente strukturelle vibrationer (10-100 Hz), mellemfrekvente driftsharmonier (100-1000 Hz) og højfrekvente strømningsinducerede vibrationer (1-10 kHz), som hver især kræver forskellige afhjælpningstilgange.
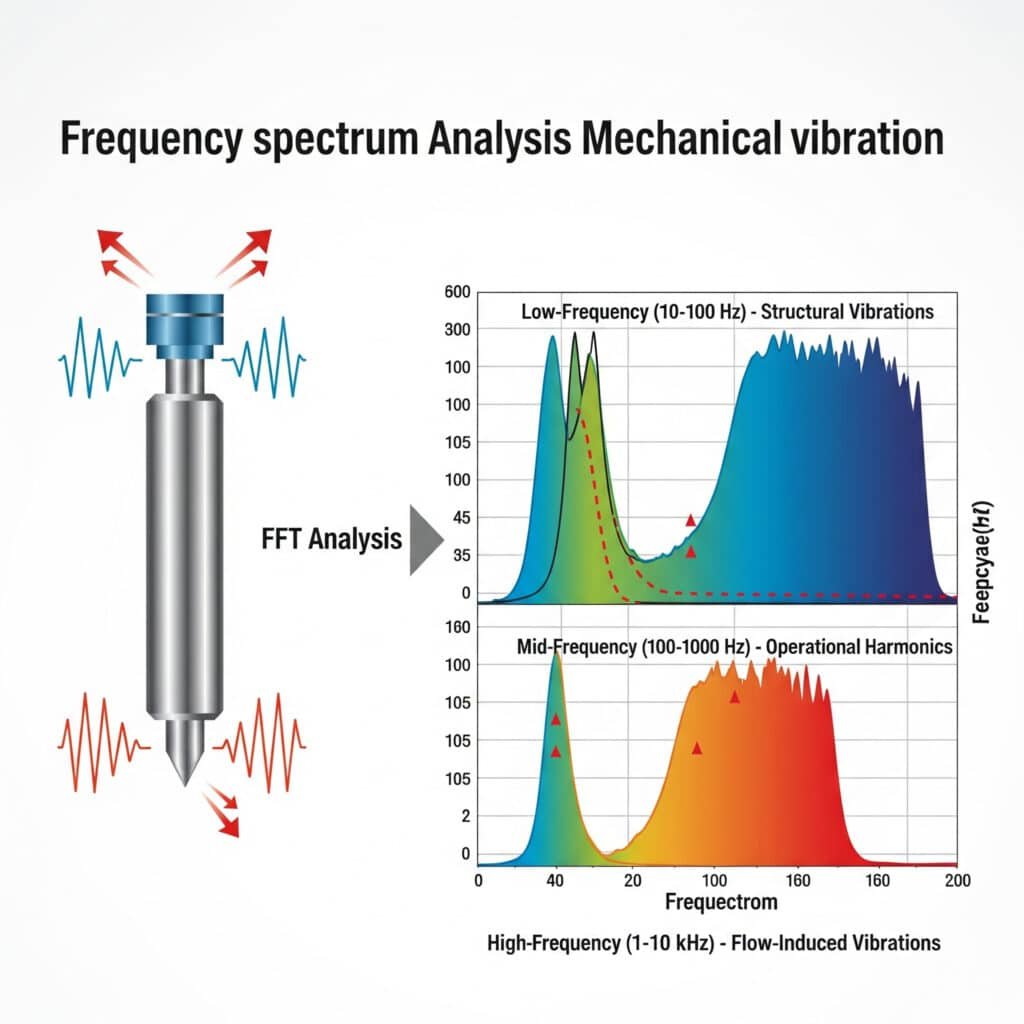
Under en konsultation hos en producent af bildele i Michigan kæmpede deres vedligeholdelsesteam med overdreven støj fra et stangløst cylinderoverførselssystem. Konventionel fejlfinding havde ikke kunnet identificere kilden. Vores analyse af vibrationsspektret afslørede en tydelig top ved 237 Hz - nøjagtigt svarende til cylinderens interne tætningsbåndresonans. Ved at ændre monteringssystemet for at dæmpe denne specifikke frekvens reducerede vi støjen med 11 dBA uden nogen form for produktionsafbrydelse.
Metode til analyse af frekvensspektrum
Effektiv vibrationsanalyse følger en systematisk tilgang:
- Opsætning af måling: Brug af accelerometre og akustiske mikrofoner
- Dataindsamling: Optagelse af vibrationssignaler i tidsdomænet
- FFT-analyse: Konvertering til frekvensdomæne
- Spektral kortlægning: Identificering af karakteristiske frekvenser
- Kildeangivelse: Matchende frekvenser til specifikke komponenter
Karakteristiske frekvensområder i pneumatiske systemer
| Frekvensområde | Typiske kilder | Akustiske egenskaber |
|---|---|---|
| 10-50 Hz | Strukturel resonans, monteringsproblemer | Lavfrekvent rumlen, der mærkes mere end den høres |
| 50-200 Hz | Stempelpåvirkning, ventilaktivering | Tydelig dunken eller banken |
| 200-500 Hz | Tætningsfriktion, intern resonans | Mellemfrekvent summen eller brummen |
| 500-2000 Hz | Flow-turbulens, trykpulseringer | Hvæsen med tonale komponenter |
| 2-10 kHz | Lækage, højhastighedsflow | Skarp hvæsen, meget irriterende for det menneskelige øre |
| >10 kHz | Mikroturbulens, gasudvidelse | Ultralydskomponenter, indikator for energitab |
Overførselsveje for vibrationer
Støj fra mekaniske vibrationer følger flere veje:
Strukturbåren transmission
Vibrationer bevæger sig gennem faste komponenter:
- Komponenten vibrerer på grund af interne kræfter
- Overførsel af vibrationer gennem monteringspunkter
- Forbundne strukturer forstærker og udstråler lyd
- Store overflader fungerer som effektive lydgivere
Luftbåren transmission
Direkte udstråling af lyd fra vibrerende overflader:
- Overfladevibrationer fortrænger luft
- Forskydning skaber trykbølger
- Bølger udbreder sig gennem luften
- Størrelsen på den udstrålende overflade bestemmer effektiviteten
Casestudie: Vibrationsanalyse af stangløse cylindre
Til en magnetisk stangløs cylinder, der udviser overdreven støj:
| Frekvens (Hz) | Amplitude (dB) | Identifikation af kilder | Afbødningsstrategi |
|---|---|---|---|
| 43 | 78 | Montering af resonans | Afstivet monteringsbeslag |
| 86 | 65 | Harmonisk af monteringsresonans | Adresseret med primær resonans |
| 237 | 91 | Forseglingsbåndets resonans | Tilføjet dæmpningsmateriale til cylinderkroppen |
| 474 | 83 | Harmonisk af tætningsbånd | Adresseret med primær resonans |
| 1250 | 72 | Turbulens i luftstrømmen | Modificeret portdesign |
| 3700 | 68 | Lækage ved endestykker | Udskiftede tætninger |
De kombinerede afhjælpningsstrategier reducerede den samlede støj med 14 dBA, hvor den mest markante forbedring kom fra håndtering af 237 Hz-resonansen.
Avancerede teknikker til vibrationsanalyse
Ud over grundlæggende FFT-analyse giver flere avancerede teknikker dybere indsigt:
Analyse af ordre
Særligt nyttig til systemer med variabel hastighed:
- Sporer frekvenser, der skalerer med driftshastigheden
- Adskiller hastighedsafhængige fra fastfrekvente komponenter
- Identificerer problemer i forbindelse med specifikke bevægelsesfaser
Analyse af operationel afbøjningsform (ODS)
Kortlægger vibrationsmønstre på tværs af hele systemet:
- Flere målepunkter skaber vibrations-"kort"
- Afslører, hvordan strukturer bevæger sig under drift
- Identificerer optimale steder til dæmpningsbehandlinger
Modal analyse
Bestemmer egenfrekvenser og tilstandsformer:
- Identificerer resonansfrekvenser før drift
- Forudser potentielle problemfrekvenser
- Styrer strukturelle ændringer for at undgå resonans
Lyddæmperens indskydningstab: Hvilke beregninger driver effektivt lyddæmperdesign?
Lyddæmpere og lyddæmpere er afgørende for at reducere støj fra pneumatiske systemer, men deres design skal være baseret på solide tekniske beregninger for at sikre effektivitet uden at gå på kompromis med systemets ydeevne.
Lyddæmper Indsættelsestab3 (IL) kvantificerer støjreduktionens effektivitet og kan beregnes som IL = Lw₁ - Lw₂, hvor Lw₁ er lydeffektniveauet uden lyddæmperen, og Lw₂ er niveauet med lyddæmperen installeret. For pneumatiske systemer opnår effektive lyddæmpere typisk 15-30 dB indsætningstab i det kritiske frekvensområde fra 500 Hz til 4 kHz, samtidig med at de opretholder et acceptabelt modtryk.
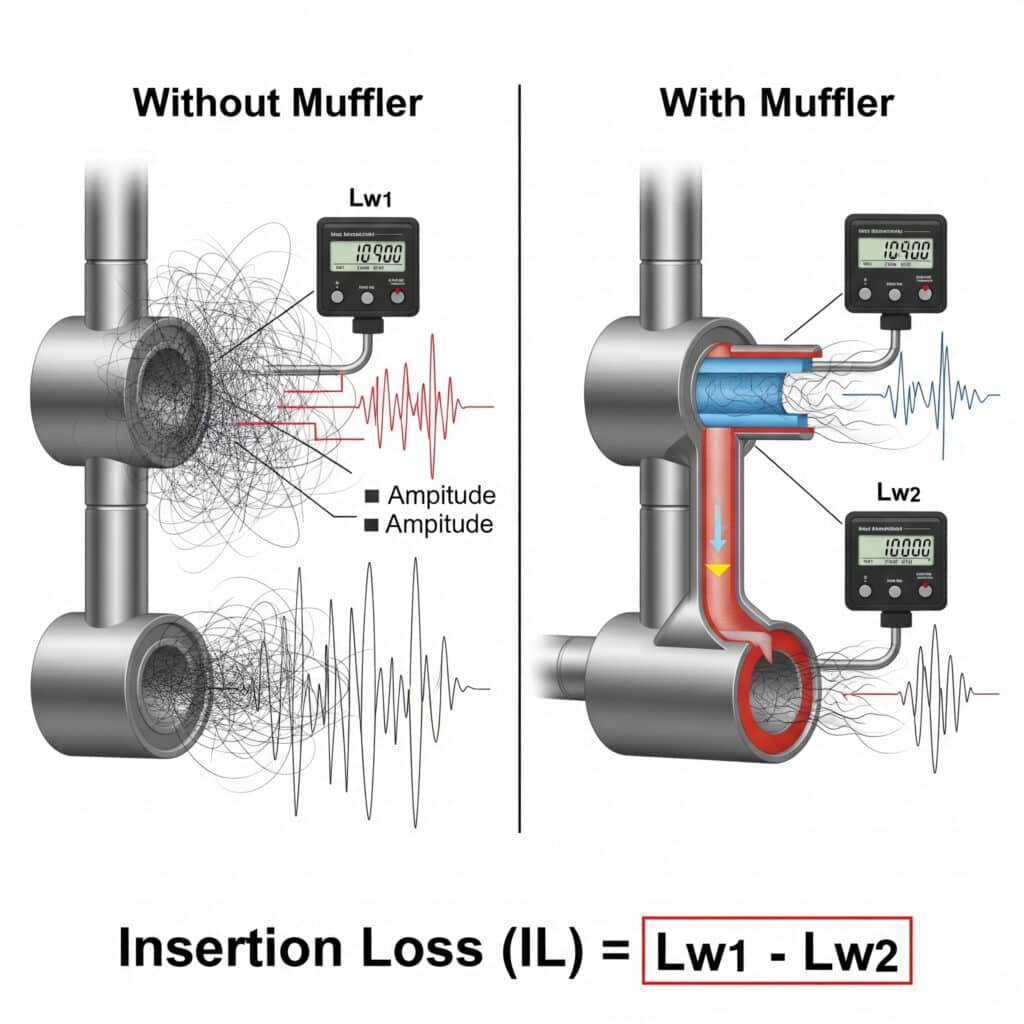
Jeg hjalp for nylig en producent af medicinsk udstyr i Massachusetts med at løse et udfordrende støjproblem med deres præcisionsstangløse cylindersystem. Deres første forsøg på at bruge lyddæmpere fra hylden reducerede støjen, men skabte et for stort modtryk, der påvirkede cyklustiderne. Ved at beregne det nødvendige indsætningstab på tværs af specifikke frekvensbånd og designe en brugerdefineret lyddæmper med flere kamre opnåede vi 24 dB støjreduktion med minimal påvirkning af ydeevnen. Resultatet var et system, der opfyldte både deres krav til støj og præcision.
Grundlæggende om lyddæmperens indsættelsestab
Kerneligningen for indsættelsestab er:
IL = Lw₁ - Lw₂
Hvor?
- IL = Indsætningsdæmpning (dB)
- Lw₁ = Lydeffektniveau uden lyddæmper (dB)
- Lw₂ = Lydeffektniveau med lyddæmper (dB)
For frekvensspecifik analyse bliver dette:
IL(f) = Lw₁(f) - Lw₂(f)
Hvor f angiver det specifikke frekvensbånd, der analyseres.
Parametre for lyddæmperdesign og deres effekt
| Parameter | Effekt på indsættelsestab | Effekt på modtryk | Optimal rækkevidde |
|---|---|---|---|
| Kammerets volumen | Større volumen øger lavfrekvent IL | Minimal påvirkning, hvis designet er korrekt | 10-30× udstødningsportens volumen |
| Antal kamre | Flere kamre øger mellemfrekvensen IL | Øges med flere kamre | 2-4 kamre til de fleste anvendelser |
| Udvidelsesgrad | Højere forholdstal forbedrer IL | Minimal påvirkning, hvis den er gradvis | 4:1 til 16:1 arealforhold |
| Akustisk materiale | Forbedrer højfrekvent IL | Minimal påvirkning med korrekt design | 10-50 mm tykkelse |
| Perforering af baffel | Påvirker mellemfrekvensen IL | Betydelig indvirkning | 30-50% åbent område |
| Flowvejens længde | Længere stier forbedrer lavfrekvent IL | Øges med længden | 3-10× portdiameter |
Teoretiske modeller til forudsigelse af indskydningstab
Flere modeller kan forudsige indsætningstab for forskellige lyddæmpertyper:
Model for ekspansionskammer
Til simple ekspansionskamre:
IL = 10 log₁₀[1 + 0,25(m-1/m)² sin²(kL)]
Hvor?
- m = Arealforhold (kammerareal/rørareal)
- k = Bølgetal (2πf/c, hvor f er frekvens og c er lydhastighed)
- L = Kammerets længde
Dissipativ lyddæmper model
Til lyddæmpere med lydabsorberende materialer:
IL = 8,68α(L/d)
Hvor?
- α = Absorptionskoefficient for materiale
- L = længden af den forede sektion
- d = Diameter på strømningsvejen
Reaktiv lyddæmper-model (Helmholtz-resonator4)
Til lyddæmpere af resonatortypen:
IL = 10 log₁₀[1 + (ρc/2S)² × (V/L'c²) × ω²/((ω₀² - ω²)² + (Rω/ρc)²)]
Hvor?
- ρ = Luftens massefylde
- c = lydens hastighed
- S = Halsens tværsnitsareal
- V = Hulrummets volumen
- L' = Effektiv halslængde
- ω = Vinkelfrekvens
- ω₀ = Resonansfrekvens
- R = Akustisk modstand
Praktisk proces for valg af lyddæmper
At vælge eller designe en passende lyddæmper:
- Mål støjspektrum: Bestem frekvensindholdet i støj
- Beregn den nødvendige IL: Bestem nødvendig reduktion efter frekvens
- Vurder behovet for flow: Beregn det maksimalt tilladte modtryk
- Vælg type lyddæmper:
- Reaktiv (ekspansionskamre) til lave frekvenser
- Dissipativ (absorberende) til høje frekvenser
- Kombination til bredbåndsstøj - Bekræft ydeevne: Test indsættelsestab og modtryk
Overvejelser om modtryk
For stort modtryk kan påvirke systemets ydeevne betydeligt:
Beregning af modtryk
Modtrykket kan beregnes som:
ΔP = ρ(Q/Cd×A)²/2
Hvor?
- ΔP = Trykfald (Pa)
- ρ = Luftens massefylde (kg/m³)
- Q = Flowhastighed (m³/s)
- Cd = udledningskoefficient
- A = Effektivt flowareal (m²)
Vurdering af resultatpåvirkning
Til en stangløs cylinder med:
- Boringsdiameter: 40 mm
- Slaglængde: 500 mm
- Cyklustid: 2 sekunder
- Driftstryk: 6 bar
Hver 0,1 bar modtryk ville gøre det:
- Reducer kraftoutput med ca. 1,7%
- Forøg cyklustiden med cirka 2,3%
- Øger energiforbruget med ca. 1,5%
Casestudie: Design af brugerdefinerede lyddæmpere
Til en præcisionsapplikation med stangløse cylindre med strenge støjkrav:
| Parameter | Udgangstilstand | Lyddæmper fra hylden | Brugerdefineret design |
|---|---|---|---|
| Lydniveau | 89 dBA | 76 dBA | 65 dBA |
| Modtryk | 0,05 bar | 0,42 bar | 0,11 bar |
| Cyklustid | 1,8 sekunder | 2,3 sekunder | 1,9 sekunder |
| Frekvensrespons | Bredbånd | Dårlig ved 2-4 kHz | Optimeret på tværs af spektret |
| Levetid | N/A | 3 måneder (tilstopning) | >12 måneder |
| Implementeringsomkostninger | N/A | $120 pr. punkt | $280 pr. punkt |
Det tilpassede lyddæmperdesign gav en overlegen støjreduktion, samtidig med at systemets ydeevne var acceptabel, og investeringen var tjent hjem på mindre end 6 måneder, når man tager produktivitetsforbedringer i betragtning.
Konklusion
Forståelse af akustiske støjgenereringsmekanismer - lydniveauer for gasudvidelse, mekaniske vibrationsspektre og beregninger af lyddæmperens indsætningstab - danner grundlaget for effektiv støjkontrol i pneumatiske systemer. Ved at anvende disse principper kan du skabe mere støjsvage, mere effektive og mere pålidelige pneumatiske systemer, samtidig med at du sikrer overholdelse af lovgivningen og forbedrer forholdene på arbejdspladsen.
Ofte stillede spørgsmål om støj fra pneumatiske systemer
Hvad er OSHA's grænser for eksponering for støj fra pneumatiske systemer?
OSHA begrænser støjeksponeringen på arbejdspladsen til 90 dBA i et 8-timers tidsvægtet gennemsnit med en vekselkurs på 5 dBA. NIOSH's anbefalede eksponeringsgrænse er dog mere konservativ og ligger på 85 dBA. Pneumatiske systemer overskrider ofte disse grænser, idet udstødningsgasser uden lyd ofte genererer 90-110 dBA på en meters afstand, hvilket kræver teknisk kontrol for at overholde dem.
Hvordan påvirker driftstrykket støj fra pneumatiske systemer?
Driftstrykket har en betydelig indvirkning på støjgenereringen, idet hver stigning i trykket på 1 bar typisk øger udstødningsstøjniveauet med 3-4 dBA. Dette forhold er logaritmisk snarere end lineært, da lydeffekten stiger med kvadratet af trykforholdet. At reducere systemtrykket til det minimum, der kræves for driften, er ofte den enkleste og mest omkostningseffektive støjreduktionsstrategi.
Hvad er forskellen på reaktive og dissipative lyddæmpere til pneumatiske systemer?
Reaktive lyddæmpere bruger kamre og passager til at reflektere lydbølger og skabe destruktiv interferens, hvilket gør dem effektive til lavfrekvent støj (under 500 Hz) med minimalt trykfald. Dissipative lyddæmpere bruger lydabsorberende materialer til at omdanne akustisk energi til varme, hvilket gør dem mere effektive til højfrekvent støj (over 500 Hz), men mere modtagelige for forurening. Mange industrielle pneumatiske lyddæmpere kombinerer begge principper til bredbåndsstøjreduktion.
Hvordan kan jeg identificere den dominerende støjkilde i mit pneumatiske system?
Brug en systematisk tilgang, der starter med driftstest: Kør systemet ved forskellige tryk, hastigheder og belastninger, mens du måler støj. Udfør derefter komponentisolering ved at betjene individuelle elementer separat. Endelig skal du foretage en frekvensanalyse ved hjælp af en lydniveaumåler med oktavbåndskapacitet - lave frekvenser (50-250 Hz) indikerer typisk strukturelle problemer, mellemfrekvenser (250-2000 Hz) tyder på driftsstøj, og høje frekvenser (2-10 kHz) peger på problemer med flow eller lækage.
Hvad er forholdet mellem støjniveau og afstand fra en pneumatisk komponent?
Støj fra pneumatiske komponenter følger den omvendte kvadratiske lov i frit felt og falder med ca. 6 dB, hver gang afstanden fordobles. Men i typiske industrimiljøer med reflekterende overflader er den faktiske reduktion ofte kun 3-4 dB pr. fordobling af afstanden på grund af efterklang. Det betyder, at en fordobling af afstanden til en støjkilde på 90 dB måske kun reducerer niveauet til 86-87 dB i stedet for de teoretiske 84 dB.
-
Indeholder de officielle OSHA-regler (Occupational Safety and Health Administration) og tilladte eksponeringsgrænser (PEL) for støj på arbejdspladsen, hvilket er en vigtig drivkraft for akustisk dæmpning. ↩
-
Forklarer Fast Fourier Transform (FFT)-algoritmen, et vigtigt matematisk værktøj, der bruges til at konvertere et tidsdomænesignal (som en vibration eller lydbølge) til de enkelte frekvenskomponenter med henblik på analyse. ↩
-
Beskriver modalanalyse, en avanceret ingeniørteknik, der bruges til at bestemme et systems iboende dynamiske egenskaber, f.eks. dets egenfrekvenser og tilstandsformer, for at forudsige og undgå resonans. ↩
-
Giver en detaljeret forklaring af Insertion Loss (IL), den primære metrik, der bruges til at kvantificere en lyddæmpers ydeevne ved at måle den lydniveaureduktion, den giver. ↩


