
Har du nogensinde rørt ved en Pneumatisk cylinder efter kontinuerlig drift og er blevet overrasket over, hvor varmt det føles? Den varme er ikke bare en ulempe - den repræsenterer spildt energi, reduceret effektivitet og potentielle pålidelighedsproblemer, som kan koste din virksomhed tusindvis af kroner.
Varmeoverførsel i pneumatiske systemer sker gennem tre mekanismer: ledning gennem komponentmaterialer, konvektion mellem overflader og luft og stråling fra varme overflader. Forståelse og optimering af disse principper kan reducere driftstemperaturerne med 15-30%, forlænge komponenternes levetid med op til 40% og forbedre energieffektiviteten med 5-15%.
I sidste måned var jeg konsulent for et fødevareforarbejdningsanlæg i Georgia, hvor deres stangløse cylindre svigtede hver 3-4 måned på grund af termiske problemer. Deres vedligeholdelsesteam udskiftede blot komponenter uden at tage fat på den grundlæggende årsag. Ved at anvende korrekte varmeoverførselsprincipper reducerede vi driftstemperaturerne med 22 °C og forlængede komponenternes levetid til over et år. Lad mig vise dig, hvordan vi gjorde det - og hvordan du kan anvende de samme principper på dine systemer.
Indholdsfortegnelse
- Beregning af ledningskoefficient: Hvordan bevæger varmen sig gennem dine komponenter?
- Metoder til forbedring af konvektion: Hvilke teknikker maksimerer luft-til-overflade-varmeoverførsel?
- Model for strålingseffektivitet: Hvornår betyder varmestråling noget i pneumatiske systemer?
- Konklusion
- Ofte stillede spørgsmål om varmeoverførsel i pneumatiske systemer
Beregning af ledningskoefficient: Hvordan bevæger varmen sig gennem dine komponenter?
Ledning er den primære varmeoverførselsmekanisme i faste pneumatiske komponenter. Det er vigtigt at forstå, hvordan man beregner og optimerer ledningskoefficienter for at kunne styre systemtemperaturer.
Varmeledningskoefficienten kan beregnes ved hjælp af Fouriers lov1: q = -k(dT/dx), hvor q er varmestrømmen (W/m²), k er varmeledningsevnen (W/m-K), og dT/dx er temperaturgradienten. For pneumatiske komponenter afhænger effektiv ledning af materialevalg, grænsefladekvalitet og geometriske faktorer, der påvirker varmebanens længde og tværsnitsareal.
Jeg husker, at jeg fejlsøgte på en produktionslinje i Tennessee, hvor de stangløse cylinderlejer svigtede for tidligt. Vedligeholdelsesteamet havde prøvet flere smøremidler uden held. Da vi analyserede ledningsvejene, opdagede vi en termisk flaskehals ved grænsefladen mellem lejet og huset. Ved at forbedre overfladefinishen og påføre en termisk ledende forbindelse øgede vi den effektive ledningskoefficient med 340% og eliminerede fejlene fuldstændigt.
Grundlæggende ledningsligninger
Lad os gennemgå de vigtigste ligninger til beregning af ledning i pneumatiske komponenter:
Fouriers lov for varmeledning
Den grundlæggende ligning for varmeledning er:
q = -k(dT/dx)
Hvor?
- q = Varmestrøm (W/m²)
- k = Varmeledningsevne (W/m-K)
- dT/dx = Temperaturgradient (K/m)
For et simpelt endimensionelt tilfælde med konstant tværsnit:
Q = kA(T₁-T₂)/L
Hvor?
- Q = Varmeoverførselshastighed (W)
- A = Tværsnitsareal (m²)
- T₁, T₂ = Temperaturer i hver ende (K)
- L = Længde af varmebane (m)
Koncept for termisk modstand
For komplekse geometrier er tilgangen med termisk modstand ofte mere praktisk:
R = L/(kA)
Hvor?
- R = Termisk modstand (K/W)
Til systemer med flere komponenter i serie:
Rtotal = R₁ + R₂ + R₃ + ... + Rₙ
Og varmeoverførselshastigheden bliver:
Q = ΔT/Rtotal
Sammenligning af materialers varmeledningsevne
| Materiale | Termisk ledningsevne (W/m-K) | Relativ ledningsevne | Almindelige anvendelser |
|---|---|---|---|
| Aluminium | 205-250 | Høj | Cylindre, køleplader |
| Stål | 36-54 | Medium | Strukturelle komponenter |
| Rustfrit stål | 14-16 | Lav-medium | Ætsende miljøer |
| Bronze | 26-50 | Medium | Lejer, bøsninger |
| PTFE | 0.25 | Meget lav | Tætninger, lejer |
| Nitrilgummi | 0.13 | Meget lav | O-ringe, tætninger |
| Luft (stadig) | 0.026 | Ekstremt lav | Udfyldning af huller |
| Termisk pasta | 3-8 | Lav | Interface-materiale |
Kontaktmodstand i pneumatiske samlinger
Ved grænseflader mellem komponenter påvirker kontaktmodstanden varmeoverførslen betydeligt:
Rcontact = 1/(hc × A)
Hvor?
- hc = Kontaktkoefficient (W/m²-K)
- A = Kontaktområde (m²)
Faktorer, der påvirker kontaktmodstanden, omfatter:
- Overfladens ruhed: Ru overflader har mindre faktisk kontaktareal
- Kontakt Tryk: Højere tryk øger det effektive kontaktområde
- Grænsefladematerialer: Termiske forbindelser udfylder luftspalter
- Overfladens renhed: Forurenende stoffer kan øge resistensen
Casestudie: Termisk optimering af stangløse cylindre
Til en magnetisk stangløs cylinder, der har termiske problemer:
| Komponent | Originalt design | Optimeret design | Forbedring |
|---|---|---|---|
| Cylinderhus | Anodiseret aluminium | Samme materiale, forbedret finish | 15% bedre ledning |
| Leje-grænseflade | Metal-til-metal-kontakt | Tilføjet termisk forbindelse | 340% bedre ledning |
| Monteringsbeslag | Lakeret stål | Blankt aluminium | 280% bedre ledning |
| Samlet termisk modstand | 2,8 K/W | 0,7 K/W | 75% reduktion |
| Driftstemperatur | 78°C | 56°C | 22°C reduktion |
| Komponenternes levetid | 4 måneder | >12 måneder | 3× forbedring |
Praktiske teknikker til optimering af ledningsføring
Baseret på min erfaring med hundredvis af pneumatiske systemer er her de mest effektive metoder til at forbedre ledningen:
Optimering af grænseflader
- Overfladebehandling: Forbedre parringsoverfladens glathed til Ra 0,4-0,8 μm
- Materialer til termisk grænseflade2: Anvend passende forbindelser (3-8 W/m-K)
- Fastgørelsesmoment: Sørg for korrekt tilspænding for optimalt kontakttryk
- Renlighed: Fjern alle olier og forureninger før montering
Strategier for materialevalg
- Kritiske varmeveje: Brug materialer med høj ledningsevne (aluminium, kobber)
- Termiske pauser: Brug bevidst materialer med lav ledningsevne for at isolere varmen
- Sammensatte tilgange: Kombiner materialer for optimal ydelse/pris
- Anisotropiske materialer: Brug retningsbestemt ledningsevne, hvor det er relevant
Geometrisk optimering
- Længde af varmebane: Minimer afstanden mellem varmekilder og dræn
- Tværsnitsareal: Maksimer arealet vinkelret på varmestrømmen
- Termiske flaskehalse: Identificer og fjern indsnævringer i varmebanen
- Overflødige stier: Skab flere parallelle ledningsveje
Metoder til forbedring af konvektion: Hvilke teknikker maksimerer luft-til-overflade-varmeoverførsel?
Konvektion er ofte den begrænsende faktor i køling af pneumatiske systemer. Forbedring af konvektiv varmeoverførsel kan dramatisk forbedre den termiske styring og systemets ydeevne.
Konvektiv varmeoverførsel følger Newtons lov om afkøling3: Q = hA(Ts-T∞), hvor h er konvektionskoefficienten (W/m²-K), A er overfladearealet, og (Ts-T∞) er temperaturforskellen mellem overfladen og væsken. Forbedringsmetoderne omfatter forøgelse af overfladearealet gennem finner, forbedring af væskehastigheden med rettet luftstrøm og optimering af overfladekarakteristika for at fremme turbulente grænselag.
Under en energieffektivitetsrevision på et pakkeanlæg i Arizona stødte jeg på et pneumatisk system, der arbejdede i et miljø på 43 °C. De stangløse cylindre blev overophedede på trods af, at de opfyldte alle vedligeholdelseskrav. Ved at implementere målrettet konvektionsforbedring - tilføje små aluminiumsfinner og en strømbesparende ventilator - øgede vi konvektionskoefficienten med 450%. Dette reducerede driftstemperaturerne fra farlige niveauer til inden for specifikationerne uden nogen større systemændringer.
Grundlæggende om konvektionsvarmeoverførsel
Den grundlæggende ligning for konvektiv varmeoverførsel er:
Q = hA(Ts-T∞)
Hvor?
- Q = Varmeoverførselshastighed (W)
- h = Konvektionskoefficient (W/m²-K)
- A = Overfladeareal (m²)
- Ts = Overfladetemperatur (K)
- T∞ = Væskens (luftens) temperatur (K)
Konvektionskoefficienten h afhænger af flere faktorer:
- Væskeegenskaber (massefylde, viskositet, varmeledningsevne)
- Strømningskarakteristika (hastighed, turbulens)
- Overfladegeometri og orientering
- Strømningsforhold (naturlig vs. tvungen konvektion)
Naturlig vs. tvungen konvektion
| Parameter | Naturlig konvektion | Tvungen konvektion | Konsekvenser |
|---|---|---|---|
| Typisk h-værdi | 5-25 W/m²-K | 25-250 W/m²-K | Tvungen konvektion kan være 10× mere effektiv |
| Den drivende kraft | Opdrift (temperaturforskel) | Eksternt tryk (ventilatorer, blæsere) | Tvungen konvektion er mindre afhængig af temperaturen |
| Flow-mønster | Lodret strømning langs overflader | Retningsbestemt baseret på tvangsmekanisme | Forceret flow kan optimeres til specifikke komponenter |
| Pålidelighed | Passiv, altid til stede | Kræver strøm og vedligeholdelse | Naturlig konvektion giver grundlæggende køling |
| Krav til plads | Kræver plads til luftcirkulation | Kræver plads til luftbevægelser og kanaler | Tvungne systemer kræver mere planlægning |
Teknikker til forbedring af konvektion
Forøgelse af overfladeareal
Øget effektivt overfladeareal gennem:
Finner og forlængede overflader
- Pin-finner: Omnidirektionel luftstrøm, 150-300% arealforøgelse
- Pladefinner: Retningsbestemt luftstrøm, 200-500% arealforøgelse
- Bølgede overflader: Moderat forbedring, 50-150% arealforøgelseRu overfladebehandling
- Mikroteksturering: 5-15% effektiv arealforøgelse
- Fordybede overflader: 10-30%-forøgelse plus grænselagseffekter
- Rillede mønstre: 15-40% øges med retningsbestemte fordele
Manipulation af flow
Forbedring af luftstrømskarakteristika gennem:
Tvangsluftsystemer
- Ventilatorer: Retningsbestemt luftstrøm, 200-600% h forbedring
- Blæsere: Højtryksflow, 300-800% h forbedring
- Komprimerede luftstråler: Målrettet køling, 400-1000% lokal h-forbedringOptimering af strømningsveje
- Baffler: Direkte luft til kritiske komponenter
- Venturi-effekter: Accelererer luft over specifikke overflader
- Hvirvelgeneratorer: Skab turbulens til forstyrrelse af grænselaget
Ændringer i overfladen
Ændring af overfladeegenskaber for at forbedre konvektionen:
Behandlinger af emissivitet
- Sort oxid: Øger emissiviteten til 0,7-0,9
- Anodisering: Kontrolleret emissivitet fra 0,4-0,9
- Maling og belægninger: Tilpasselig emissivitet op til 0,98Kontrol af befugtning
- Hydrofile belægninger: Forbedrer væskekøling
- Hydrofobe overflader: Forhindrer problemer med kondens
- Mønstret befugtningsevne: Målrettet kondensatstrømning
Praktisk eksempel på implementering
Til en stangløs pneumatisk cylinder, der arbejder i et miljø med høje temperaturer:
| Forbedringsmetode | Implementering | h Forbedring | Reduktion af temperatur |
|---|---|---|---|
| Pin Fins (6 mm) | Aluminiumsfinner, der kan klikkes på, 10 mm afstand | 180% | 12°C |
| Målrettet luftstrøm | 80 mm, 2 W DC-blæser ved 1,5 m/s | 320% | 18°C |
| Overfladebehandling | Sort anodisering | 40% | 3°C |
| Kombineret tilgang | Alle metoder integreret | 450% | 24°C |
Nusselt-tal-korrelation til designberegninger
Til tekniske beregninger skal Nusselt-tal4 (Nu) giver en dimensionsløs tilgang til konvektion:
Nu = hL/k
Hvor?
- L = Karakteristisk længde
- k = Væskens varmeledningsevne
For tvungen konvektion over en flad plade:
Nu = 0,664Re^(1/2)Pr^(1/3) (laminar strømning)
Nu = 0,037Re^(4/5)Pr^(1/3) (turbulent strømning)
Hvor?
- Re = Reynolds tal (hastighed × længde × massefylde / viskositet)
- Pr = Prandtl-tal (specifik varme × viskositet / varmeledningsevne)
Disse sammenhænge gør det muligt for ingeniører at forudsige konvektionskoefficienter for forskellige konfigurationer og optimere kølestrategier i overensstemmelse hermed.
Model for strålingseffektivitet: Hvornår betyder varmestråling noget i pneumatiske systemer?
Stråling bliver ofte overset i termisk styring af pneumatiske systemer, men den kan stå for 15-30% af den samlede varmeoverførsel i mange applikationer. At forstå, hvornår og hvordan man optimerer strålingsvarmeoverførsel, er afgørende for omfattende varmestyring.
Strålingsvarmeoverførsel følger Stefan-Boltzmanns lov5: Q = εσA(T₁⁴-T₂⁴), hvor ε er overfladens emissivitet, σ er Stefan-Boltzmann-konstanten, A er overfladearealet, og T₁ og T₂ er de absolutte temperaturer på den emitterende overflade og omgivelserne. Udstrålingseffektiviteten i pneumatiske systemer afhænger primært af overfladens emissivitet, temperaturforskelle og synsfaktorer mellem komponenter og deres omgivelser.
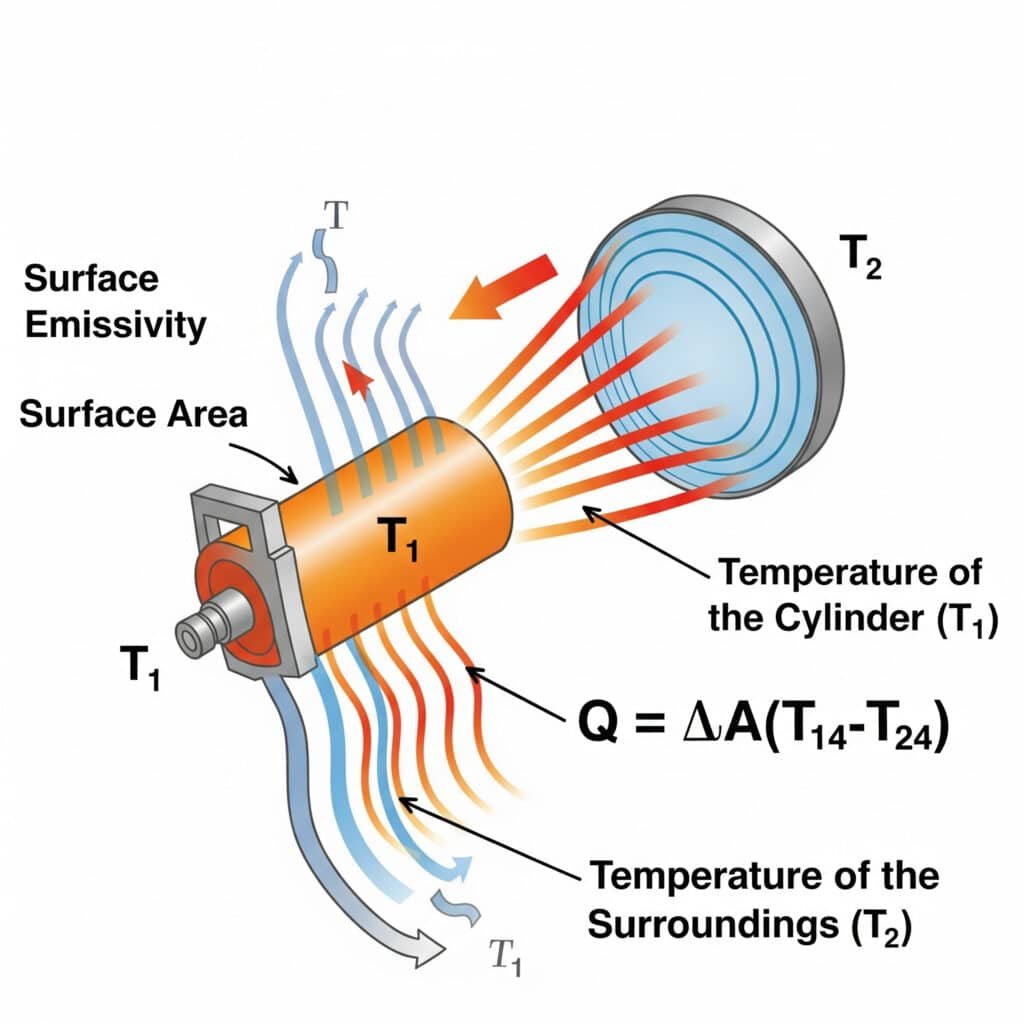
Jeg hjalp for nylig en producent af halvlederudstyr i Oregon med at løse problemer med overophedning af deres præcisionscylindre uden stænger. Deres ingeniører havde udelukkende fokuseret på ledning og konvektion, men overset stråling. Ved at påføre en belægning med høj emissivitet (øge ε fra 0,11 til 0,92) forbedrede vi strålingsvarmeoverførslen med over 700%. Denne enkle, passive løsning reducerede driftstemperaturen med 9 °C uden nogen bevægelige dele eller energiforbrug - et kritisk krav i deres renrumsmiljø.
Grundlæggende om varmeoverførsel ved stråling
Den grundlæggende ligning, der styrer strålingsvarmeoverførsel, er:
Q = εσA(T₁⁴-T₂⁴)
Hvor?
- Q = Varmeoverførselshastighed (W)
- ε = Emissivitet (dimensionsløs, 0-1)
- σ = Stefan-Boltzmann-konstant (5,67 × 10-⁸ W/m²-K⁴)
- A = Overfladeareal (m²)
- T₁ = Overfladens absolutte temperatur (K)
- T₂ = Omgivelsernes absolutte temperatur (K)
Overfladeemissivitetsværdier for almindelige pneumatiske materialer
| Materiale/overflade | Emissivitet (ε) | Strålingseffektivitet | Forbedringspotentiale |
|---|---|---|---|
| Poleret aluminium | 0.04-0.06 | Meget dårlig | >1500% forbedring mulig |
| Anodiseret aluminium | 0.7-0.9 | Fremragende | Allerede optimeret |
| Rustfrit stål (poleret) | 0.07-0.14 | Dårlig | >600% forbedring mulig |
| Rustfrit stål (oxideret) | 0.6-0.85 | God | Moderat forbedring mulig |
| Stål (poleret) | 0.07-0.10 | Dårlig | >900% forbedring mulig |
| Stål (oxideret) | 0.7-0.9 | Fremragende | Allerede optimeret |
| Malede overflader | 0.8-0.98 | Fremragende | Allerede optimeret |
| PTFE (hvid) | 0.8-0.9 | Fremragende | Allerede optimeret |
| Nitrilgummi | 0.86-0.94 | Fremragende | Allerede optimeret |
Se faktorovervejelser
Strålingsudveksling afhænger ikke kun af emissivitet, men også af geometriske forhold mellem overflader:
F₁₂ = Fraktion af stråling, der forlader overflade 1 og rammer overflade 2
For komplekse geometrier kan visningsfaktorer beregnes ved hjælp af:
- Analytiske løsninger for simple geometrier
- Se faktor-algebra til at kombinere kendte løsninger
- Numeriske metoder til komplekse arrangementer
- Empiriske tilnærmelser til praktisk ingeniørarbejde
Strålingens temperaturafhængighed
Temperaturforholdet med fjerde potens gør stråling særlig effektiv ved højere temperaturer:
| Overfladetemperatur | Procentdel af varmeoverførsel ved stråling*. |
|---|---|
| 30°C (303K) | 5-15% |
| 50°C (323K) | 10-25% |
| 75°C (348K) | 15-35% |
| 100°C (373K) | 25-45% |
| 150°C (423K) | 35-60% |
*Forudsat naturlig konvektion, ε = 0,8, 25 °C omgivende.
Strategier til forbedring af strålingseffektiviteten
Baseret på min erfaring med industrielle pneumatiske systemer er her de mest effektive metoder til at forbedre strålingsvarmeoverførslen:
Ændring af overfladens emissivitet
Belægninger med høj emissivitet
- Sort anodisering til aluminium (ε ≈ 0,8-0,9)
- Sort oxid til stål (ε ≈ 0,7-0,8)
- Specielle keramiske belægninger (ε ≈ 0,9-0,98)Teksturering af overflader
- Mikroruhed øger den effektive emissivitet
- Porøse overflader forbedrer udstrålingsegenskaberne
- Kombinerede forbedringer af emissivitet/konvektion
Miljømæssig optimering
Styring af omgivelsernes temperatur
- Afskærmning fra varmt udstyr/processer
- Kølige vægge/lofter for bedre udveksling af stråling
- Reflekterende barrierer for at lede stråling til køligere overfladerSe faktorforbedring
- Orientering for at maksimere eksponering for kølige overflader
- Fjernelse af blokerende genstande
- Reflektorer for at forbedre udvekslingen af stråling med køligere områder
Casestudie: Forbedring af stråling i præcisionspneumatik
Til en stangløs cylinder med høj præcision i et renrumsmiljø:
| Parameter | Originalt design | Strålingsforbedret design | Forbedring |
|---|---|---|---|
| Overflademateriale | Poleret aluminium (ε ≈ 0,06) | Keramisk belagt aluminium (ε ≈ 0,94) | 1467% stigning i emissivitet |
| Strålingsvarmeoverførsel | 2.1W | 32.7W | 1457% stigning i stråling |
| Driftstemperatur | 68°C | 59°C | 9°C reduktion |
| Komponenternes levetid | 8 måneder | >24 måneder | 3× forbedring |
| Implementeringsomkostninger | – | $175 pr. cylinder | 4,2 måneders tilbagebetaling |
Stråling vs. andre former for varmeoverførsel
At forstå, hvornår stråling dominerer, er afgørende for effektiv varmestyring:
| Tilstand | Ledningsdominans | Konvektionens dominans | Strålingsdominans |
|---|---|---|---|
| Temperaturområde | Lav til høj | Lav til middel | Middel til høj |
| Materialeegenskaber | Materialer med højt k | Lavt k, højt overfladeareal | Overflader med høj ε |
| Miljømæssige faktorer | God termisk kontakt | Luft i bevægelse, ventilatorer | Stor temperaturforskel |
| Begrænsning af plads | Tæt emballage | Åben luftstrøm | Udsigt til køligere omgivelser |
| Bedste applikationer | Komponenternes grænseflader | Generel køling | Varme overflader, vakuum, stillestående luft |
Konklusion
Beherskelse af varmeoverførselsprincipper - beregning af ledningskoefficient, metoder til forbedring af konvektion og modellering af strålingseffektivitet - giver grundlaget for effektiv termisk styring i pneumatiske systemer. Ved at anvende disse principper kan du reducere driftstemperaturerne, forlænge komponenternes levetid og forbedre energieffektiviteten, samtidig med at du sikrer pålidelig drift selv i udfordrende miljøer.
Ofte stillede spørgsmål om varmeoverførsel i pneumatiske systemer
Hvad er den typiske temperaturstigning i pneumatiske cylindre under drift?
Pneumatiske cylindre oplever typisk temperaturstigninger på 20-40 °C over omgivelsestemperaturen under kontinuerlig drift. Denne stigning skyldes friktion mellem tætninger og cylindervægge, kompressionsopvarmning af luft og mekanisk arbejde, der omdannes til varme. Stangløse cylindre oplever ofte højere temperaturstigninger (30-50 °C) på grund af deres mere komplekse tætningssystemer og den koncentrerede varmeudvikling i leje-/tætningsenheden.
Hvordan påvirker driftstrykket varmeudviklingen i pneumatiske systemer?
Driftstrykket har en betydelig indvirkning på varmeudviklingen, idet højere tryk skaber mere varme gennem flere mekanismer. Hver stigning på 1 bar i driftstryk øger typisk varmeudviklingen med 8-12% på grund af større friktionskræfter mellem tætninger og overflader, højere kompressionsopvarmning og øgede lækagerelaterede tab. Dette forhold er omtrent lineært inden for normale driftsområder (3-10 bar).
Hvad er den optimale kølemetode for pneumatiske komponenter i forskellige miljøer?
Den optimale kølemetode varierer fra miljø til miljø: I rene miljøer med moderate temperaturer (15-30 °C) er naturlig konvektion med korrekt afstand mellem komponenterne ofte tilstrækkelig. I miljøer med høje temperaturer (30-50 °C) er det nødvendigt med tvungen konvektion ved hjælp af ventilatorer eller trykluft. Under ekstremt varme forhold (>50 °C), eller hvor luftstrømmen er begrænset, kan det være nødvendigt med aktive kølemetoder som termoelektriske kølere eller væskekøling. I alle tilfælde giver maksimering af stråling gennem overflader med høj emissivitet yderligere passiv køling.
Hvordan beregner jeg den samlede varmeoverførsel fra en pneumatisk komponent?
Beregn den samlede varmeoverførsel ved at lægge bidragene fra hver mekanisme sammen: Qtotal = Qledning + Qkonvektion + Qstråling. For ledning skal du bruge Q = kA(T₁-T₂)/L for hver varmevej. For konvektion skal du bruge Q = hA(Ts-T∞) med passende konvektionskoefficienter. For stråling skal du bruge Q = εσA(T₁⁴-T₂⁴). I de fleste industrielle pneumatiske applikationer, der arbejder ved 30-80 °C, er den omtrentlige fordeling 20-40% ledning, 40-70% konvektion og 10-30% stråling.
Hvad er forholdet mellem temperatur og pneumatiske komponenters levetid?
Komponenternes levetid falder eksponentielt med stigende temperatur efter et modificeret Arrhenius-forhold. Som tommelfingerregel reducerer hver stigning på 10 °C i driftstemperaturen levetiden for tætninger og komponenter med 40-50%. Det betyder, at en komponent, der arbejder ved 70 °C, måske kun holder en tredjedel så længe som den samme komponent ved 50 °C. Dette forhold er særligt kritisk for polymerkomponenter som tætninger, lejer og pakninger, som ofte bestemmer vedligeholdelsesintervallet for pneumatiske systemer.
-
Giver en grundlæggende forklaring på Fouriers lov, det fundamentale princip, der beskriver, hvordan varme ledes gennem faste materialer baseret på deres varmeledningsevne og temperaturgradient. ↩
-
Forklarer funktionen og typerne af termiske grænsefladematerialer (TIM), som bruges til at fylde mikroskopiske luftspalter mellem komponenter for at forbedre varmeledningen og reducere den termiske modstand. ↩
-
Beskriver principperne i Newtons lov om afkøling, som styrer, hvordan objekter afkøles ved at overføre varme til den omgivende væske via konvektion, en nøglefaktor i design af systemkøling. ↩
-
Tilbyder et dybdegående kig på Nusselt-tallet, en kritisk dimensionsløs størrelse inden for væskedynamik og varmeoverførsel, der repræsenterer forholdet mellem konvektiv og konduktiv varmeoverførsel over en grænse. ↩
-
Beskriver Stefan-Boltzmanns lov, det grundlæggende fysiske princip, der kvantificerer den samlede energi, der udstråles af et sort legeme, hvilket er afgørende for at beregne varmetab fra varme overflader. ↩


