Ingeniører fejlberegner ofte stangområder, når de designer pneumatiske cylindersystemer, hvilket fører til forkerte kraftberegninger og fejl i systemets ydeevne.
Stangarealet er det cirkulære tværsnitsareal beregnet som A = πr² eller A = π(d/2)², hvor 'r' er stangens radius og 'd' er stangens diameter, hvilket er afgørende for kraft- og trykberegninger.
I går hjalp jeg Carlos, en designingeniør fra Mexico, hvis pneumatiske system mislykkedes, fordi han glemte at trække stangarealet fra stempelarealet i sine beregninger af den dobbeltvirkende cylinders kraft.
Indholdsfortegnelse
- Hvad er stangområdet i pneumatiske cylindersystemer?
- Hvordan beregner man stangens tværsnitsareal?
- Hvorfor er stangarealet vigtigt for kraftberegninger?
- Hvordan påvirker stangarealet cylinderens ydeevne?
Hvad er stangområdet i pneumatiske cylindersystemer?
Stangarealet repræsenterer stempelstangens cirkulære tværsnitsareal, som er afgørende for beregning af effektive stempelarealer og kraftoutput i dobbeltvirkende pneumatiske cylindre.
Stempelstangens areal er det cirkulære areal, som stempelstangens tværsnit optager, målt vinkelret på stempelstangens akse, og som bruges til at bestemme effektive nettoarealer til kraftberegninger.
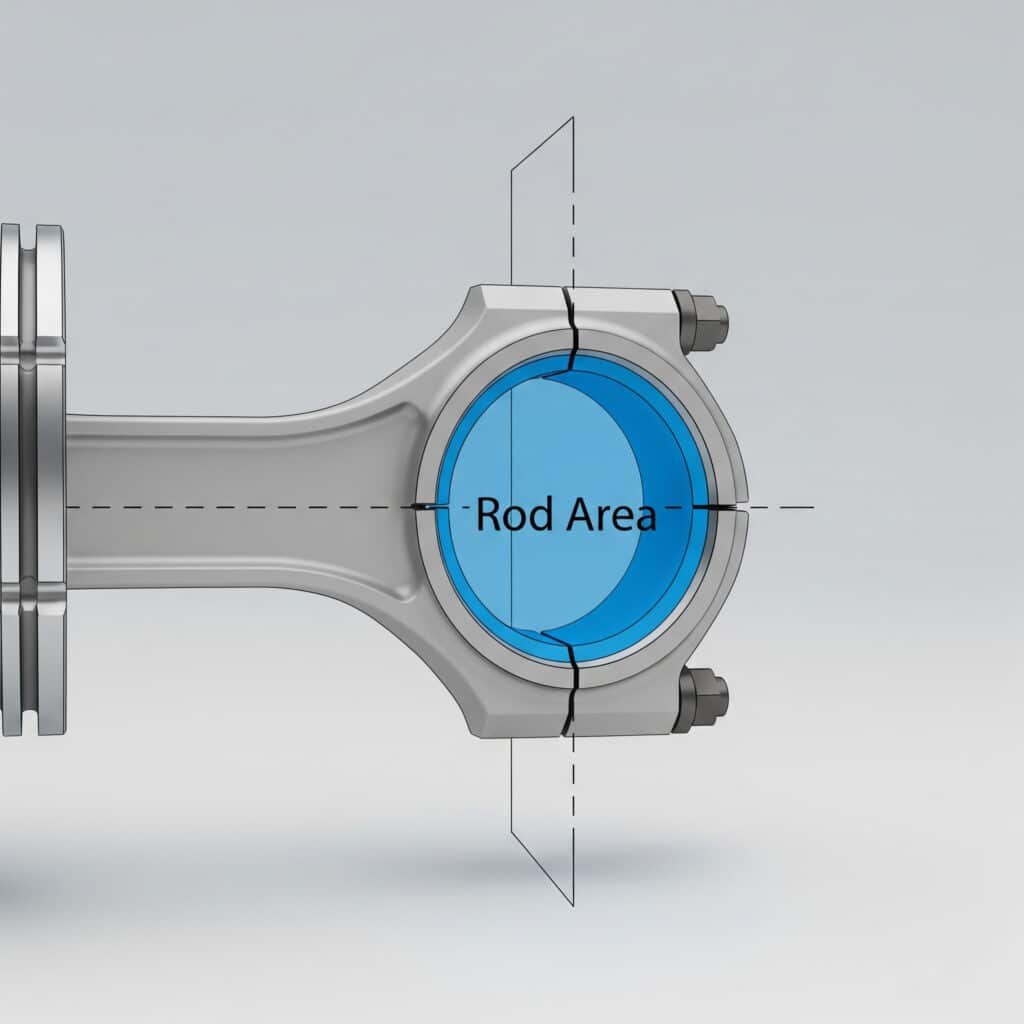
Definition af stangområde
Geometriske egenskaber
- Cirkulært tværsnit: Standard stanggeometri
- Vinkelret måling: 90° til stangens midterlinje
- Konstant areal: Ensartet langs stangens længde
- Fast område: Komplet tværsnit af materiale
Vigtige målinger
- Stangens diameter: Primær dimension til arealberegning
- Stangens radius: Halvdelen af diametermålingen
- Tværsnitsareal: Anvendelse af cirkulær arealformel
- Effektivt område: Indvirkning på cylinderens ydeevne
Forholdet mellem stang- og stempelareal
| Komponent | Formel for areal | Formål | Anvendelse |
|---|---|---|---|
| Stempel | A = π(D/2)² | Område med fuld boring | Udvidelse af kraftberegning |
| Rod | A = π(d/2)² | Tværsnit af stang | Beregning af tilbagetrækningskraft |
| Nettoareal | A_stempel - A_stang | Effektivt tilbagetrækningsområde | Dobbeltvirkende cylindre |
| Ringformet område1 | π(D² - d²)/4 | Ringformet område | Tryk på stangsiden |
Standard stangstørrelser
Almindelige stangdiametre
- 8 mm stang: Areal = 50,3 mm²
- 12 mm stang: Areal = 113,1 mm²
- 16 mm stang: Areal = 201,1 mm²
- 20 mm stang: Areal = 314,2 mm²
- 25 mm stang: Areal = 490,9 mm²
- 32 mm stang: Areal = 804,2 mm²
Forhold mellem stang og boring
- Standardforhold: Stangdiameter = 0,5 × boringsdiameter
- Tungt arbejde: Stangdiameter = 0,6 × boringsdiameter
- Let arbejde: Stangdiameter = 0,4 × boringsdiameter
- Tilpassede applikationer: Varierer efter behov
Anvendelser i stangområdet
Beregning af kraft
Jeg bruger stangområdet til:
- Forlæng kraften: Fuldt stempelareal × tryk
- Træk kraften tilbage: (Stempelareal - stangareal) × tryk
- Kraftforskel: Forskel på at forlænge/tilbagetrække
- Belastningsanalyse: Matchende cylinder til anvendelse
Systemdesign
Stangområdet påvirker:
- Valg af cylinder: Korrekt dimensionering til applikationer
- Beregning af hastighed: Flowkrav for hver retning
- Krav til tryk: Specifikationer for systemtryk
- Optimering af ydeevne: Afbalanceret driftsdesign
Stangareal i forskellige cylindertyper
Enkeltvirkende cylindre
- Ingen påvirkning af stangområdet: Fjederreturfunktion
- Forlæng kun kraften: Fuldt effektivt stempelområde
- Forenklede beregninger: Ingen overvejelser om tilbagetrækningskraft
- Optimering af omkostninger: Reduceret kompleksitet
Dobbeltvirkende cylindre
- Stangens område er kritisk: Påvirker tilbagetrækningskraften
- Asymmetrisk drift: Forskellige kræfter i hver retning
- Komplekse beregninger: Skal overveje begge områder
- Afbalancering af ydeevne: Nødvendige designovervejelser
Stangløse cylindre
- Intet stangområde: Elimineret fra design
- Symmetrisk drift: Lige store kræfter i begge retninger
- Forenklede beregninger: Overvejelser om et enkelt område
- Fordele ved plads: Ingen krav om forlængelse af stangen
Hvordan beregner man stangens tværsnitsareal?
Beregning af stangens tværsnitsareal bruger standardformlen for cirkulært areal med målinger af stangens diameter eller radius til nøjagtigt design af pneumatiske systemer.
Beregn stangens areal ved hjælp af A = πr² (med radius) eller A = π(d/2)² (med diameter), hvor π = 3,14159, og sørg for ensartede enheder i hele beregningen.
Grundlæggende arealformel
Brug af stangradius
A = πr²
- A: Stangens tværsnitsareal
- π: 3.14159 (matematisk konstant)
- r: Stangens radius (diameter ÷ 2)
- Enheder: Areal i radius-enheder i kvadrat
Brug af stangdiameter
A = π(d/2)² eller A = πd²/4
- A: Stangens tværsnitsareal
- π: 3.14159
- d: Stangens diameter
- Enheder: Areal i diameterenheder i kvadrat
Trin-for-trin-beregning
Måleproces
- Mål stangens diameter: Brug skydelære for nøjagtighed
- Bekræft måling: Tag flere aflæsninger
- Beregn radius: r = diameter ÷ 2 (hvis du bruger radiusformlen)
- Anvend formel: A = πr² eller A = π(d/2)²
- Tjek enheder: Sørg for et ensartet enhedssystem
Eksempel på beregning
Til en stang med en diameter på 20 mm:
- Metode 1: A = π(10)² = π × 100 = 314,16 mm²
- Metode 2: A = π(20)²/4 = π × 400/4 = 314,16 mm²
- Bekræftelse: Begge metoder giver identiske resultater
Tabel til beregning af stangareal
| Stangens diameter | Stangens radius | Beregning af areal | Stangområde |
|---|---|---|---|
| 8 mm | 4 mm | π × 4² | 50,3 mm² |
| 12 mm | 6 mm | π × 6² | 113,1 mm² |
| 16 mm | 8 mm | π × 8² | 201,1 mm² |
| 20 mm | 10 mm | π × 10² | 314,2 mm² |
| 25 mm | 12,5 mm | π × 12.5² | 490,9 mm² |
| 32 mm | 16 mm | π × 16² | 804,2 mm² |
Værktøjer til måling
Digitale skydelærer
- Nøjagtighed: ±0,02 mm præcision
- Rækkevidde: 0-150 mm typisk
- Funktioner: Digitalt display, konvertering af enheder
- Bedste praksis: Flere målepunkter
Mikrometer
- Nøjagtighed: ±0,001 mm præcision
- Rækkevidde: Forskellige størrelser til rådighed
- Funktioner: Skralde-stop, digitale indstillinger
- Anvendelser: Krav om høj præcision
Almindelige beregningsfejl
Fejl i målingerne
- Diameter vs. radius: Brug af forkert dimension i formel
- Uoverensstemmelse mellem enheder: Blanding af mm og tommer
- Præcisionsfejl: For få decimaler
- Kalibrering af værktøj: Ukalibrerede måleinstrumenter
Formelfejl
- Forkert formel: Brug af omkreds i stedet for areal
- Mangler π: Glemmer matematisk konstant
- Kvadreringsfejl: Forkert anvendelse af eksponent
- Omregning af enheder: Ukorrekte enhedstransformationer
Verifikationsmetoder
Teknikker til krydstjek
- Flere beregninger: Forskellige formelmetoder
- Verifikation af målinger: Gentag målinger af diameter
- Referencetabeller: Sammenlign med standardværdier
- CAD-software: Beregning af 3D-modellens areal
Kontrol af rimelighed
- Korrelation mellem størrelser: Større diameter = større areal
- Standard-sammenligninger: Match typiske stangstørrelser
- Egnethed til anvendelse: Passende til cylinderstørrelse
- Produktionsstandarder: Almindelige tilgængelige størrelser
Avancerede beregninger
Hule stænger
A = π(D² - d²)/4
- D: Udvendig diameter
- d: Indvendig diameter
- Anvendelse: Vægtreduktion, intern routing
- Beregning: Træk det indre område fra det ydre område
Ikke-cirkulære stænger
- Firkantede stænger: A = side²
- Rektangulære stænger: A = længde × bredde
- Særlige former: Brug passende geometriske formler
- Anvendelser: Forhindre rotation, særlige krav
Da jeg arbejdede med Jennifer, en pneumatisk systemdesigner fra Canada, beregnede hun oprindeligt stangarealet forkert ved at bruge diameter i stedet for radius i πr²-formlen, hvilket resulterede i 4× overvurdering og helt forkerte kraftberegninger for hendes dobbeltvirkende cylinderapplikation.
Hvorfor er stangarealet vigtigt for kraftberegninger?
Stangarealet påvirker direkte det effektive stempelareal på stangsiden af dobbeltvirkende cylindre, hvilket skaber kraftforskelle mellem ud- og indtrækningsoperationer.
Stangarealet reducerer det effektive stempelareal under tilbagetrækning, hvilket skaber lavere tilbagetrækningskraft sammenlignet med udtrækskraft i dobbeltvirkende cylindre, hvilket kræver kompensation i systemdesignet.
Grundlæggende kraftberegning
Grundlæggende kraftformel
- Forlæng kraften: F = P × A_piston
- Træk kraften tilbage: F = P × (A_stempel - A_stang)
- Kraftforskel: Udtrækskraft > Indtrækskraft
- Påvirkning af design: Skal overveje begge retninger
Effektive områder
- Fuldt stempelområde: Tilgængelig under forlængelse
- Netto stempelareal: Stempelareal minus stangareal under tilbagetrækning
- Ringformet område: Ringformet område på stangens side
- Arealforhold: Bestemmer kraftdifferentiale
Eksempler på kraftberegning
63 mm boring, 20 mm stangcylinder
- Stempelområde: π(31,5)² = 3.117 mm²
- Stangens område: π(10)² = 314 mm²
- Nettoareal: 3.117 - 314 = 2.803 mm²
- Ved 6 bar tryk:
– Forlæng kraften: 6 × 3,117 = 18,702 N
– Træk kraften tilbage: 6 × 2,803 = 16,818 N
– Kraftforskel: 1.884 N (10%-reduktion)
Tabel til sammenligning af kræfter
| Cylinderstørrelse | Stempelområde | Stangområde | Nettoareal | Kraftforhold |
|---|---|---|---|---|
| 32mm/12mm | 804 mm² | 113 mm² | 691 mm² | 86% |
| 50mm/16mm | 1.963 mm² | 201 mm² | 1.762 mm² | 90% |
| 63mm/20mm | 3.117 mm² | 314 mm² | 2.803 mm² | 90% |
| 80mm/25mm | 5.027 mm² | 491 mm² | 4.536 mm² | 90% |
| 100 mm/32 mm | 7,854 mm² | 804 mm² | 7.050 mm² | 90% |
Påvirkning af applikation
Matchning af belastning
- Forlæng belastningen: Kan håndtere fuld nominel kraft
- Træk belastninger tilbage: Begrænset af reduceret effektivt område
- Udligning af belastning: Overvej kraftforskelle i designet
- Sikkerhedsmarginer: Tag højde for reduceret tilbagetrækningsevne
Systemets ydeevne
- Forskelle i hastighed: Forskellige flowkrav i hver retning
- Krav til tryk: Kan have brug for højere tryk for at trække sig tilbage
- Kontrol af kompleksitet: Overvejelser om asymmetrisk drift
- Energieffektivitet: Optimer til begge retninger
Overvejelser om design
Valg af stangstørrelse
- Standardforhold: Stangdiameter = 0,5 × boringsdiameter
- Tunge belastninger: Større stang for strukturel styrke
- Kraftbalance: Mindre stang for mere ensartede kræfter
- Applikationsspecifik: Tilpassede forhold til særlige krav
Strategier til afbalancering af kræfter
- Kompensation af tryk: Højere tryk på stangsiden
- Kompensation for areal: Større cylinder til krav om tilbagetrækning
- Dobbelte cylindre: Separate cylindre til hver retning
- Stangløst design: Eliminer effekter på stangens område
Praktiske anvendelser
Materialehåndtering
- Løfteapplikationer: Forlæng kraften kritisk
- Skubbeoperationer: Kan have brug for tilpasning af tilbagetrækningskraft
- Spændesystemer: Kraftforskellen påvirker holdekraften
- Positioneringsnøjagtighed: Kraftvariationer påvirker præcisionen
Produktionsprocesser
- Tryk på operationer: Konsistente styrkekrav
- Monteringssystemer: Præcis kraftkontrol nødvendig
- Kvalitetskontrol: Kraftvariationer påvirker produktkvaliteten
- Cyklustid: Kraftforskelle slaghastighed
Fejlfinding af force-problemer
Almindelige problemer
- Utilstrækkelig tilbagetrækningskraft: Lasten er for tung til netområdet
- Ujævn drift: Kraftforskelle skaber problemer
- Variationer i hastighed: Forskellige krav til flow
- Kontrolproblemer: Asymmetriske responsegenskaber
Løsninger
- Opskalering af cylinder: Større boring for tilstrækkelig tilbagetrækningskraft
- Justering af tryk: Optimer til kritisk retning
- Optimering af stangstørrelse: Balance mellem styrke og kraftbehov
- Redesign af systemet: Overvej stangløse alternativer
Da jeg rådførte mig med Michael, en maskinbygger fra Australien, fungerede hans pakkeudstyr ikke konsekvent, fordi han kun havde designet det til udtrækskraft. 15%'s reduktion af tilbagetrækningskraften forårsagede fastklemning under returløbet, hvilket krævede en større cylinder for at kunne håndtere begge retninger korrekt.
Hvordan påvirker stangarealet cylinderens ydeevne?
Stangarealet har stor indflydelse på cylinderhastighed, kraftoutput, energiforbrug og den samlede systemydelse i pneumatiske applikationer.
Større stangarealer reducerer tilbagetrækningskraften og øger tilbagetrækningshastigheden på grund af mindre effektivt areal og reducerede krav til luftmængde, hvilket skaber asymmetriske cylinderegenskaber.
Påvirkning af hastighed og ydeevne
Forhold mellem flowhastigheder
Hastighed = Flowhastighed3 ÷ Effektivt areal
- Forlæng hastigheden: Flow ÷ fuldt stempelareal
- Tilbagetrækningshastighed: Flow ÷ (stempelareal - stangareal)
- Hastighedsforskel: Trækker sig typisk hurtigere tilbage
- Optimering af flow: Forskellige krav i hver retning
Eksempel på beregning af hastighed
Til 63 mm boring, 20 mm stang ved 100 l/min flow:
- Forlæng hastigheden: 100.000 ÷ 3.117 = 32,1 mm/s
- Tilbagetrækningshastighed: 100.000 ÷ 2.803 = 35,7 mm/s
- Øget hastighed: 11% hurtigere tilbagetrækning
Karakteristika for ydeevne
Effekter af kraftoutput
| Stangstørrelse | Reduktion af styrke | Øget hastighed | Påvirkning af ydeevne |
|---|---|---|---|
| Lille (d/D = 0,3) | 9% | 10% | Minimal asymmetri |
| Standard (d/D = 0,5) | 25% | 33% | Moderat asymmetri |
| Stor (d/D = 0,6) | 36% | 56% | Betydelig asymmetri |
Energiforbrug
- Forlæng slagtilfælde: Fuld luftmængde påkrævet
- Tilbagetrækningsslag: Reduceret luftmængde (stangforskydning)
- Energibesparelser: Lavere forbrug under tilbagetrækning
- Systemets effektivitet: Samlet energioptimering mulig
Analyse af luftforbrug
Beregning af volumen
- Forlæng volumen: Stempelareal × slaglængde
- Træk volumen tilbage: (Stempelareal - stangareal) × slaglængde
- Forskel i volumen: Besparelser på stangvolumen
- Påvirkning af omkostninger: Reducerede krav til kompressor
Eksempel på forbrug
100 mm boring, 32 mm stang, 500 mm slaglængde:
- Forlæng volumen: 7.854 × 500 = 3.927.000 mm³
- Træk volumen tilbage: 7.050 × 500 = 3.525.000 mm³
- Besparelser: 402.000 mm³ (10% reduktion)
Optimering af systemdesign
Kriterier for valg af stangstørrelse
- Strukturelle krav: Bøjning4 og bøjningsbelastninger
- Kraftbalance: Acceptabel kraftforskel
- Krav til hastighed: Ønskede hastighedskarakteristika
- Energieffektivitet: Optimering af luftforbrug
- Overvejelser om omkostninger: Materiale- og produktionsomkostninger
Afbalancering af ydeevne
- Kontrol af flow: Separat regulering for hver retning
- Kompensation af tryk: Juster til kraftbehov
- Tilpasning af hastighed: Gasser hurtigere retning, hvis det er nødvendigt
- Belastningsanalyse: Match cylinder til applikationskrav
Applikationsspecifikke overvejelser
Højhastighedsapplikationer
- Små stænger: Minimér hastighedsforskellen
- Optimering af flow: Størrelse på ventiler for hver retning
- Kontrol af kompleksitet: Håndter asymmetrisk respons
- Krav til præcision: Tag højde for hastighedsvariationer
Anvendelse til tunge opgaver
- Store stænger: Prioritet for strukturel styrke
- Kraftkompensation: Accepter reduceret tilbagetrækningskraft
- Belastningsanalyse: Sørg for tilstrækkelig kapacitet i begge retninger
- Sikkerhedsfaktorer: Konservativ designtilgang
Overvågning af ydeevne
Nøgleindikatorer for performance
- Konsistent cyklustid: Overvåg hastighedsvariationer
- Kraftudgang: Bekræft tilstrækkelig kapacitet
- Energiforbrug: Spor forbrugsmønstre for luft
- Systemtryk: Optimer til effektivitet
Retningslinjer for fejlfinding
- Langsom tilbagetrækning: Tjek for for stort stangareal
- Utilstrækkelig kraft: Bekræft beregningerne af det effektive areal
- Ujævne hastigheder: Juster flowkontrol
- Højt energiforbrug: Optimer valg af stangstørrelse
Avancerede præstationskoncepter
Dynamisk respons
- Forskelle i acceleration: Masse- og områdeeffekter
- Resonans-egenskaber: Variationer i naturlig frekvens
- Kontrol af stabilitet: Asymmetrisk systemadfærd
- Positioneringsnøjagtighed: Påvirkning af hastighedsforskelle
Termiske effekter
- Varmeudvikling: Højere i udstrækningsretningen
- Temperaturstigning: Påvirker konsistensen af ydeevnen
- Krav til afkøling: Kan have brug for forbedret varmeafledning
- Materialeudvidelse: Overvejelser om termisk vækst
Data om ydeevne i den virkelige verden
Resultater af casestudie
Analyse af 100 installationer viste:
- Standard stangforhold: 10-15% hastighedsdifferentiale typisk
- Overdimensionerede stænger: Op til 50% hastighedsforøgelse ved tilbagetrækning
- Underdimensionerede stænger: Strukturelle fejl i 25% af tilfældene
- Optimerede designs: Afbalanceret ydeevne kan opnås
Da jeg optimerede cylindervalget for Lisa, en emballageingeniør fra Storbritannien, reducerede vi hendes stangstørrelse fra 0,6 til 0,5 boreforhold, hvilket forbedrede kraftbalancen med 20%, samtidig med at vi opretholdt tilstrækkelig strukturel styrke og reducerede variationer i cyklustiden med 30%.
Konklusion
Stangens areal er lig med π(d/2)² ved brug af stangens diameter 'd'. Dette areal reducerer den effektive tilbagetrækningskraft i dobbeltvirkende cylindre, hvilket skaber hastigheds- og kraftforskelle, der kræver overvejelser i det pneumatiske systemdesign.
Ofte stillede spørgsmål om Rod Area
Hvordan beregner man stangens areal?
Beregn stangens areal ved hjælp af A = π(d/2)², hvor 'd' er stangens diameter, eller A = πr², hvor 'r' er stangens radius. For en stang med en diameter på 20 mm: A = π(10)² = 314,2 mm².
Hvorfor er stangarealet vigtigt i pneumatiske cylindre?
Stangarealet reducerer det effektive stempelareal under tilbagetrækning i dobbeltvirkende cylindre, hvilket skaber lavere tilbagetrækningskraft sammenlignet med udtrækskraft. Dette påvirker kraftberegninger, hastighedsegenskaber og systemets ydeevne.
Hvordan påvirker stangens areal cylinderkraften?
Stangarealet reducerer tilbagetrækningskraften med den mængde: Tilbagetrækningskraft = tryk × (stempelareal - stangareal). En 20 mm stang i en 63 mm cylinder reducerer tilbagetrækningskraften med ca. 10% sammenlignet med udtrækningskraften.
Hvad sker der, hvis man ignorerer stangens areal i beregningerne?
At ignorere stangarealet fører til overvurderede beregninger af tilbagetrækningskraften, underdimensionerede cylindre til tilbagetrækningsbelastninger, forkerte hastighedsforudsigelser og potentielle systemfejl, når den faktiske ydeevne ikke stemmer overens med designforventningerne.
Hvordan påvirker stangstørrelsen cylinderens ydeevne?
Større stænger reducerer tilbagetrækningskraften mere, men øger tilbagetrækningshastigheden på grund af det mindre effektive areal. Standard stangforhold (d/D = 0,5) giver en god balance mellem strukturel styrke og kraftsymmetri i de fleste anvendelser.
-
Forstå definitionen og beregningen af ringformede områder i tekniske sammenhænge. ↩
-
Udforsk det grundlæggende fysiske princip, Pascals lov, som styrer væskekraftsystemer. ↩
-
Opdag principperne for strukturel knækning, en kritisk fejltilstand for slanke komponenter under kompression. ↩
-
Gennemgå definitionen af flowhastighed og dens rolle i beregningen af hastigheden i væskesystemer. ↩



