
Kæmper du med inkonsekvente pneumatiske cylinderhastigheder eller uventede slag i slutningen af slaget? Disse almindelige problemer skyldes ofte en dårlig forståelse af stempelkinematik. Mange ingeniører fokuserer udelukkende på kraftkrav, mens de overser de kritiske bevægelsesparametre, der bestemmer systemets ydeevne.
Stempel-kinematik1 har direkte indflydelse på pneumatiske systemers ydeevne gennem tryk-hastighedsforhold, accelerationsgrænser og krav til dæmpning. Ved at forstå disse principper kan ingeniører dimensionere komponenter korrekt, forudsige faktiske bevægelsesprofiler og forhindre for tidlige fejl i stangløse cylindre og andre pneumatiske aktuatorer.
I mine mere end 15 år hos Bepto, hvor jeg har arbejdet med pneumatiske systemer, har jeg set utallige tilfælde, hvor forståelsen af disse grundlæggende principper har hjulpet kunderne med at løse vedvarende problemer med ydeevnen og forlænge udstyrets levetid med 3-5 gange.
Indholdsfortegnelse
- Hvilket tryk har du egentlig brug for til bevægelse med konstant hastighed?
- Hvordan beregner man den maksimalt mulige acceleration i pneumatiske cylindre?
- Hvorfor er dæmpningstiden vigtig, og hvordan beregnes den?
- Konklusion
- Ofte stillede spørgsmål om stempelkinematik i pneumatiske systemer
Hvilket tryk har du egentlig brug for til bevægelse med konstant hastighed?
Mange ingeniører anvender simpelthen det maksimale tilgængelige tryk på deres pneumatiske systemer, men denne tilgang er ineffektiv og kan føre til rykvise bevægelser, overdreven slitage og spildt energi.
Det tryk, der kræves for bevægelse med konstant hastighed i en pneumatisk cylinder, beregnes ved hjælp af P = (F + Fr)/A, hvor P er tryk, F er den eksterne belastningskraft, Fr er friktionsmodstanden, og A er stempelarealet. Denne beregning sikrer jævn, effektiv drift uden for højt tryk, der spilder energi og fremskynder slid på komponenterne.
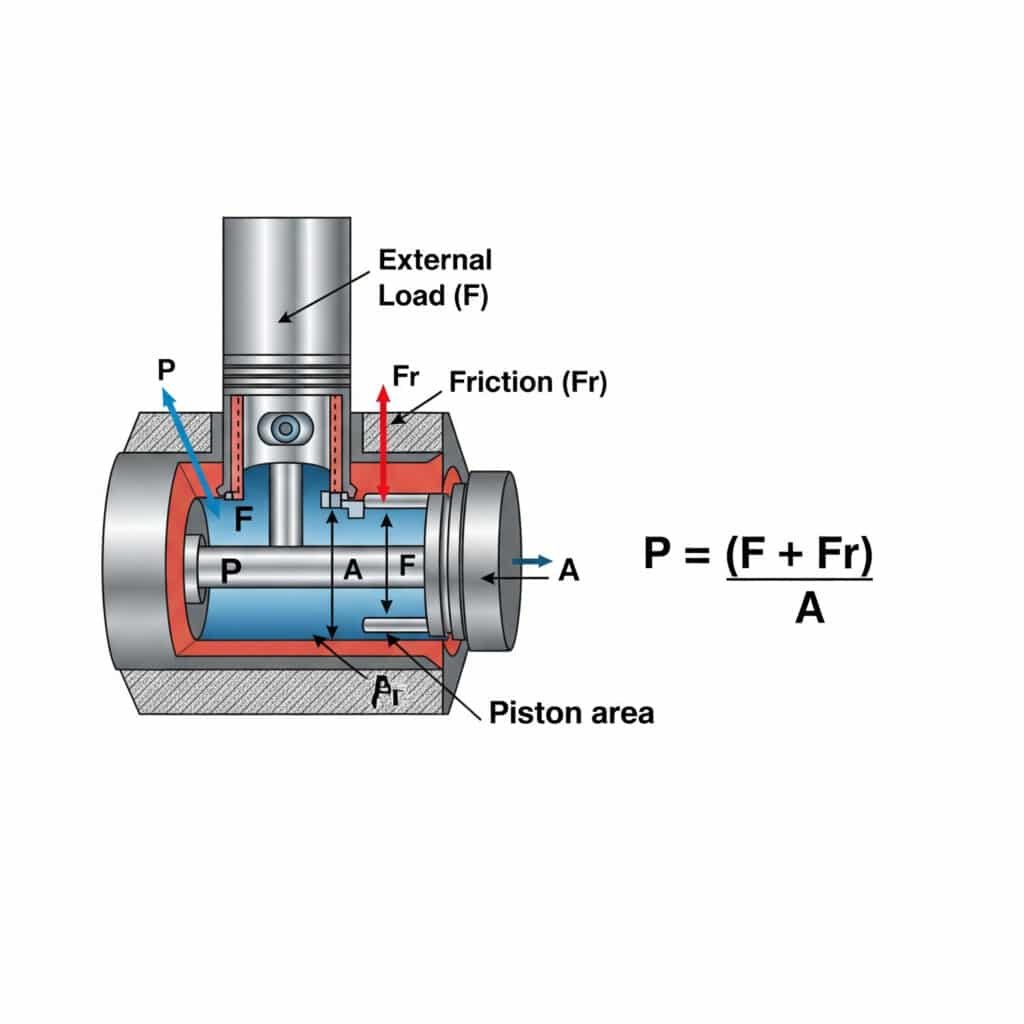
At forstå trykkravene til bevægelse med konstant hastighed har praktiske konsekvenser for systemdesign og drift. Lad mig dele det op i praktisk anvendelige indsigter.
Faktorer, der påvirker trykbehovet ved konstant hastighed
Det tryk, der skal til for at opretholde en konstant hastighed, afhænger af flere faktorer:
| Faktor | Indvirkning på trykbehov | Praktiske overvejelser |
|---|---|---|
| Ekstern belastning | Direkte lineært forhold | Varierer med orientering og eksterne kræfter |
| Friktion | Øger det nødvendige tryk | Ændringer med tætningsslitage og smøring |
| Stempelområde | Omvendt proportional | Større boring = lavere trykbehov |
| Begrænsninger i lufttilførslen | Trykfald i ledninger/ventiler | Dimensionér komponenter til minimalt trykfald |
| Modtryk | Er imod forslaget | Overvej udstødningsflowets kapacitet |
Beregning af minimumstryk for stabil bevægelse
At bestemme det minimumstryk, der er nødvendigt for en stabil bevægelse:
- Beregn den kraft, der skal til for at overvinde den eksterne belastning
- Tilføj friktionskraften (typisk 3-20% af den maksimale kraft)
- Divider med det effektive stempelareal
- Tilføj en stabilitetsfaktor (typisk 10-30%)
For eksempel i en stangløs cylinder med 40 mm boring, 10 kg belastning og 15% friktion:
| Parameter | Beregning | Resultat |
|---|---|---|
| Belastningskraft | 10 kg × 9,81 m/s² | 98.1N |
| Friktionskraft | 15% af maksimal kraft ved 6 bar | ~45N |
| Samlet styrke | 98,1N + 45N | 143.1N |
| Stempelområde | π × (0,02m)² | 0.00126m² |
| Minimumstryk | 143,1N ÷ 0,00126m² | 113.571 Pa (1,14 bar) |
| Med 20% Stabilitetsfaktor | 1,14 bar × 1,2 | 1,37 bar |
Anvendelse i den virkelige verden: Energibesparelser gennem trykoptimering
Sidste år arbejdede jeg sammen med Robert, en produktionsingeniør på en møbelfabrik i Michigan. Hans automatiserede samlebånd brugte stangløse cylindre, der arbejdede med hele 6 bars forsyningstryk, uanset belastning.
Efter at have analyseret hans applikation fandt vi ud af, at de fleste bevægelser kun krævede 2,5-3 bar for at fungere stabilt. Ved at installere Proportionale trykregulatorerreducerede vi luftforbruget med 40%, mens vi bibeholdt den samme cyklustid. Det sparede ca. $12.000 årligt i energiomkostninger, samtidig med at det reducerede sliddet på tætningerne og forlængede vedligeholdelsesintervallerne.
Forholdet mellem hastighed og tryk i virkelige systemer
I praksis er forholdet mellem tryk og hastighed ikke helt lineært på grund af:
- Begrænsning af flow: Ventil- og portdimensionering påvirker den maksimalt opnåelige hastighed
- Effekter af kompressibilitet: Luft er komprimerbar, hvilket forårsager accelerationsforsinkelser
- Stick-slip-fænomener: Friktionsegenskaber ændres med hastigheden
- Inerti-effekter: Masseacceleration kræver ekstra kraft/tryk
Hvordan beregner man den maksimalt mulige acceleration i pneumatiske cylindre?
At forstå accelerationsgrænser er afgørende for at forhindre for store stød, vibrationer og for tidlige komponentfejl i pneumatiske systemer.
Den maksimalt mulige acceleration i en pneumatisk cylinder beregnes ved hjælp af a = (P × A - F - Fr)/m, hvor a er acceleration, P er tryk, A er stempelareal, F er ekstern belastning, Fr er friktionsmodstand, og m er den bevægelige masse. Denne ligning definerer de fysiske grænser for, hvor hurtigt en pneumatisk aktuator kan starte eller stoppe en bevægelse.
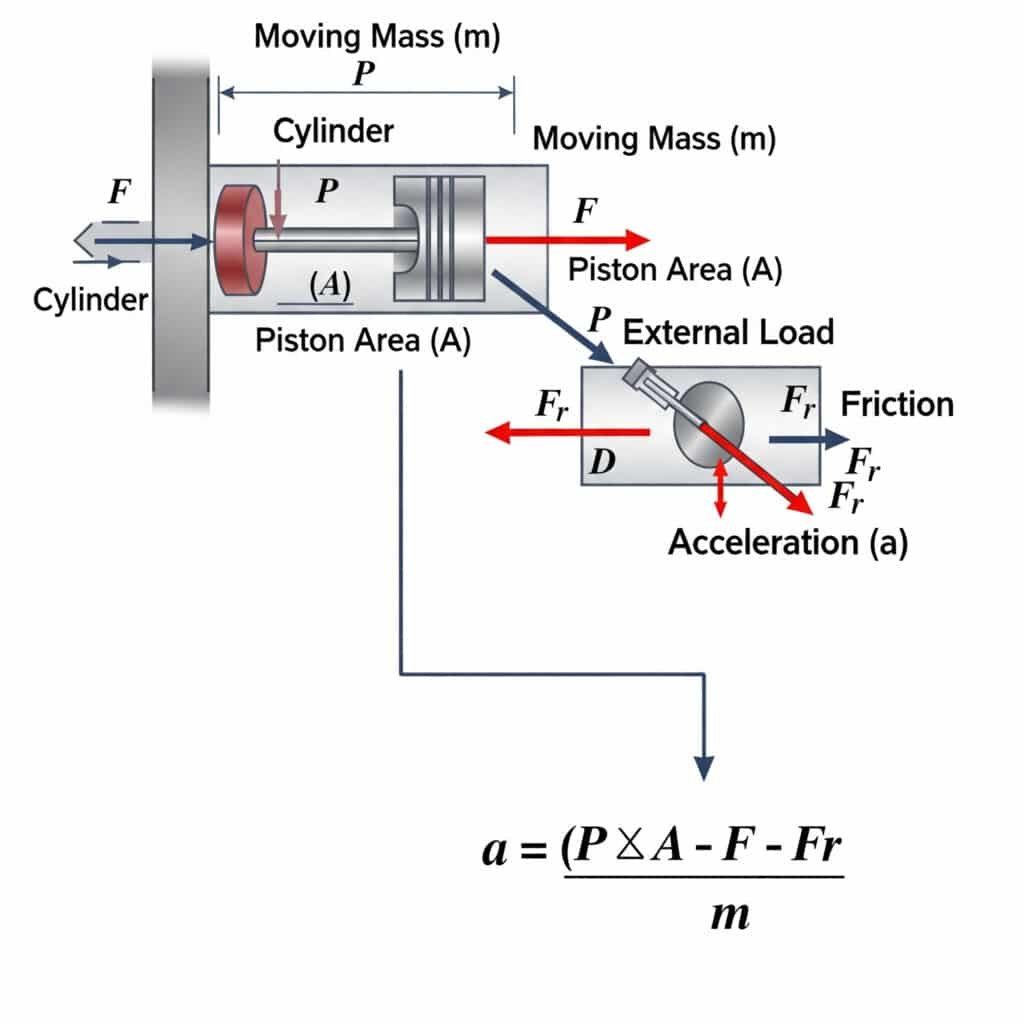
De teoretiske accelerationsgrænser har betydelige praktiske konsekvenser for systemdesign og valg af komponenter.
Udledning af accelerationsgrænselignelsen
Ligningen for accelerationsgrænsen kommer fra Newtons anden lov2 (F = ma):
- Den nettokraft, der er til rådighed for acceleration, er: Fnet = Ftryk - Fbelastning - Ffriktion
- F-tryk = P × A
- Derfor: a = Fnet/m = (P × A - F - Fr)/m
Praktiske accelerationsgrænser for forskellige cylindertyper
Forskellige cylinderdesigns har forskellige praktiske accelerationsgrænser:
| Cylindertype | Typisk maks. acceleration | Begrænsende faktorer |
|---|---|---|
| Standard stangcylinder | 10-15 m/s² | Knæk i stangen, lejebelastninger |
| Stangløs cylinder (magnetisk) | 8-12 m/s² | Magnetisk koblingsstyrke |
| Stangløs cylinder (mekanisk) | 15-25 m/s² | Design af tætning/leje, intern friktion |
| Styrecylinder | 20-30 m/s² | Styresystemets stivhed, bæreevne |
| Slagcylinder | 50-100+ m/s² | Specielt designet til høj acceleration |
Masseovervejelser i accelerationsberegninger
Når man beregner acceleration, er det vigtigt at medregne alle bevægelige masser:
- Stempelsamling: Inkluderer stempel, tætninger og forbindelseselementer
- Belastning af masse: Ekstern last flyttes
- Effektiv masse af luft i bevægelse: Ofte ubetydelig, men relevant i højhastighedsapplikationer
- Tilføjet masse på grund af monteringskomponenter: Beslag, sensorer osv.
Jeg hjalp engang en kunde i Frankrig, som oplevede mystiske fejl i sit stangløse cylindersystem. Cylinderen var dimensioneret korrekt til den angivne belastning på 15 kg, men svigtede konsekvent efter et par tusinde cyklusser.
Efter at have undersøgt sagen opdagede vi, at han havde glemt at tage højde for monteringspladens og tilbehørets masse på 12 kg. Den faktiske masse i bevægelse var næsten dobbelt så stor, som han havde beregnet, hvilket forårsagede accelerationskræfter, der overskred cylinderens designgrænser. Efter at have opgraderet til en større cylinder stoppede fejlene helt.
Metoder til kontrol af acceleration
At kontrollere accelerationen inden for sikre grænser:
- Flowreguleringsventiler: Begræns flowhastigheden under den første bevægelse
- Proportionale ventiler: Sørg for kontrolleret opstart af tryk
- Acceleration i flere trin: Brug trinvise trykstigninger
- Mekanisk dæmpning: Tilføj eksterne støddæmpere
- Elektronisk kontrol: Brug servo-pneumatiske systemer3 med feedback om acceleration
Hvorfor er dæmpningstiden vigtig, og hvordan beregnes den?
Korrekt dæmpning i slutningen af slaget er afgørende for at forhindre slagskader, reducere støj og forlænge levetiden for pneumatiske cylindre. Forståelse af dæmpningstiden hjælper ingeniører med at designe systemer, der afbalancerer cyklustiden med komponenternes levetid.
Dæmpningstiden i pneumatiske cylindre beregnes ved hjælp af ligningen t = √(2s/a), hvor t er tid, s er dæmpningsslaglængde, og a er deceleration. Denne tid repræsenterer, hvor lang tid det tager at bremse den bevægelige masse sikkert inden sammenstødet, hvilket er afgørende for at forhindre skader på cylinderen og de tilknyttede komponenter.

Lad os udforske de praktiske aspekter af beregninger af dæmpningstiden og deres betydning for systemdesign.
Fysikken bag pneumatisk dæmpning
Pneumatisk dæmpning fungerer gennem kontrolleret luftkompression og begrænset udstødning:
- Når stemplet kommer ind i pudekammeret, er udstødningsvejen begrænset
- Den indespærrede luft komprimeres, hvilket skaber et stigende modtryk
- Dette modtryk skaber en modkraft, der bremser stemplet.
- Decelerationsprofilen afhænger af pudens design og justering.
Beregning af optimal dæmpningstid
Den optimale dæmpningstid afbalancerer forebyggelse af stød med effektiv cyklustid:
| Parameter | Formel | Eksempel |
|---|---|---|
| Afstand til støddæmpning | Baseret på cylinderdesign | 15 mm (typisk for 40 mm boring) |
| Nødvendig deceleration | a = v²/(2s) | For v=0,5m/s, s=15mm: a = 8,33m/s² |
| Dæmpende tid | t = √(2s/a) | t = √(2×0,015/8,33) = 0,06s |
| Opbygning af tryk | P = P₀(V₀/V)^γ | Afhænger af pudekammerets geometri |
Faktorer, der påvirker støddæmpningens ydeevne
Flere faktorer påvirker den faktiske støddæmpning:
- Pudeforseglingsdesign: Påvirker luftlækage under støddæmpning
- Justering af nåleventil: Kontrollerer udstødningsbegrænsningens hastighed
- Masse i bevægelse: Tungere belastninger kræver længere dæmpningstid
- Indflyvningshastighed: Højere hastigheder kræver længere pudeafstand
- Driftstryk: Påvirker den maksimale tilgængelige modkraft
Dæmpningstyper og deres anvendelse
Forskellige dæmpningsmekanismer er velegnede til forskellige anvendelser:
| Type støddæmpning | Karakteristika | Bedste applikationer |
|---|---|---|
| Fast støddæmpning | Enkel, ikke-justerbar | Lette belastninger, ensartet drift |
| Justerbar støddæmpning | Kan indstilles med nåleventiler | Varierende belastninger, fleksible anvendelser |
| Selvjusterende støddæmpning | Tilpasser sig forskellige forhold | Ændring af hastigheder og belastninger |
| Eksterne støddæmpere | Høj energiabsorption | Tunge belastninger, høje hastigheder |
| Elektronisk dæmpning | Præcis kontrolleret deceleration | Servo-pneumatiske systemer |
Casestudie: Optimering af dæmpning i applikationer med høj cyklus
Jeg arbejdede for nylig sammen med Thomas, en designingeniør hos en producent af bilkomponenter i Tyskland. Hans samlebånd brugte stangløse cylindre, der arbejdede med 45 cyklusser i minuttet, men oplevede hyppige tætningsfejl og skader på monteringsbeslaget.
Analysen viste, at dæmpningstiden var for kort til den bevægelige masse, hvilket forårsagede slagkræfter på næsten 3G i hver ende af slaget. Ved at øge dæmpningsslaget fra 12 mm til 20 mm og optimere nåleventilindstillingerne forlængede vi dæmpningstiden fra 0,04 s til 0,07 s.
Denne tilsyneladende lille ændring reducerede slagkræfterne med over 60%, eliminerede skader på beslaget fuldstændigt og forlængede tætningernes levetid fra 3 måneder til over et år - alt sammen mens den krævede cyklustid blev opretholdt.
Praktisk procedure for justering af dæmpning
For optimal dæmpning i stangløse cylindre:
- Start med helt åbne pudeventiler (minimal begrænsning)
- Luk gradvist pudeventilen, indtil der er opnået en jævn deceleration
- Test med minimale og maksimale forventede belastninger
- Bekræft støddæmpningens ydeevne over hele hastighedsområdet
- Lyt efter stødlyde, der indikerer utilstrækkelig støddæmpning
- Mål den faktiske decelerationstid for at bekræfte beregningerne
Konklusion
At forstå principperne for stempelkinematik - fra trykkrav til konstant hastighed til accelerationsgrænser og beregning af dæmpningstid - er afgørende for at designe effektive, pålidelige pneumatiske systemer. Ved at anvende disse principper på dine applikationer med stangløse cylindre kan du optimere ydeevnen, reducere energiforbruget og forlænge komponenternes levetid betydeligt.
Ofte stillede spørgsmål om stempelkinematik i pneumatiske systemer
Hvilket tryk skal jeg bruge til en bestemt cylinderhastighed?
Det nødvendige tryk afhænger af belastningen, friktionen og cylinderarealet. Beregn det ved hjælp af P = (F + Fr)/A, hvor F er den eksterne belastningskraft, Fr er friktionsmodstanden, og A er stempelarealet. For en typisk stangløs cylinder, der flytter en 10 kg tung last horisontalt, skal du bruge ca. 1,5-2 bar for at opnå en stabil bevægelse ved moderate hastigheder.
Hvor hurtigt kan en pneumatisk cylinder accelerere?
En pneumatisk cylinders maksimale acceleration beregnes ved hjælp af a = (P × A - F - Fr)/m. Typiske stangløse cylindre kan opnå en acceleration på 10-25 m/s² afhængigt af designet. Det svarer til at nå en hastighed på 0,5 m/s på ca. 20-50 millisekunder under optimale forhold.
Hvilke faktorer begrænser den maksimale hastighed for en stangløs cylinder?
Den maksimale hastighed er begrænset af ventilens flowkapacitet, lufttilførselsvolumen, portstørrelse, dæmpningsevne og tætningsdesign. De fleste stangløse standardcylindre er designet til maksimale hastigheder på 0,8-1,5 m/s, men specialiserede højhastighedsdesigns kan nå op på 2-3 m/s.
Hvordan beregner jeg den rette dæmpning til min applikation?
Beregn den korrekte dæmpning ved at bestemme den kinetiske energi (KE = ½mv²) i din bevægelige last og sikre, at dit dæmpningssystem kan absorbere denne energi. Dæmpningstiden skal beregnes ved hjælp af t = √(2s/a), hvor s er dæmpningsafstanden, og a er den ønskede decelerationshastighed.
Hvad sker der, hvis min pneumatiske cylinder accelererer for hurtigt?
Overdreven acceleration kan forårsage mekanisk stress på monteringskomponenter, for tidlig tætningsslitage, øget vibration og støj, potentiel lastforskydning eller skade og reduceret systempræcision. Det kan også føre til rykvise bevægelser, der påvirker produktkvaliteten i præcisionsapplikationer.
Hvordan påvirker belastningens retning det tryk, der kræves for at bevæge sig?
Lastens retning har stor indflydelse på trykbehovet. Lodrette belastninger, der bevæger sig mod tyngdekraften, kræver ekstra tryk for at overvinde tyngdekraften (P = F/A + Fg/A + Fr/A). Vandrette belastninger behøver kun at overvinde friktion og inerti. Hældningsbelastninger falder mellem disse ekstremer baseret på vinklens sinus.
-
Giver en grundlæggende forklaring på kinematik, den gren af mekanikken, der beskriver objekters bevægelse uden at tage hensyn til de kræfter, der forårsager bevægelsen.
elektronisk indgangssignal, hvilket muliggør avanceret pneumatisk styring. ↩ -
Detaljer om Newtons anden lov (F=ma), det grundlæggende fysiske princip, der relaterer den kraft, der virker på et objekt, til dets masse og acceleration, og som er grundlaget for alle dynamiske beregninger. ↩
-
Beskriver servopneumatik, en avanceret styringsteknologi, der kombinerer kraften i pneumatik med præcisionen i elektronisk styring med lukket kredsløb for at opnå meget nøjagtige positionerings- og bevægelsesprofiler. ↩



