Αντιμετωπίζετε προβλήματα με αργές ταχύτητες κυλίνδρων, ασυνεπή κίνηση ή ανεπαρκή δύναμη στα πνευματικά σας συστήματα; Αυτά τα κοινά προβλήματα συχνά οφείλονται σε έναν παρεξηγημένο ένοχο: την αντίσταση ροής. Πολλοί μηχανικοί διαστασιολογούν τα πνευματικά τους εξαρτήματα με βάση αποκλειστικά τις απαιτήσεις πίεσης και δύναμης, παραβλέποντας τον κρίσιμο αντίκτυπο της αντίστασης ροής στην πραγματική απόδοση.
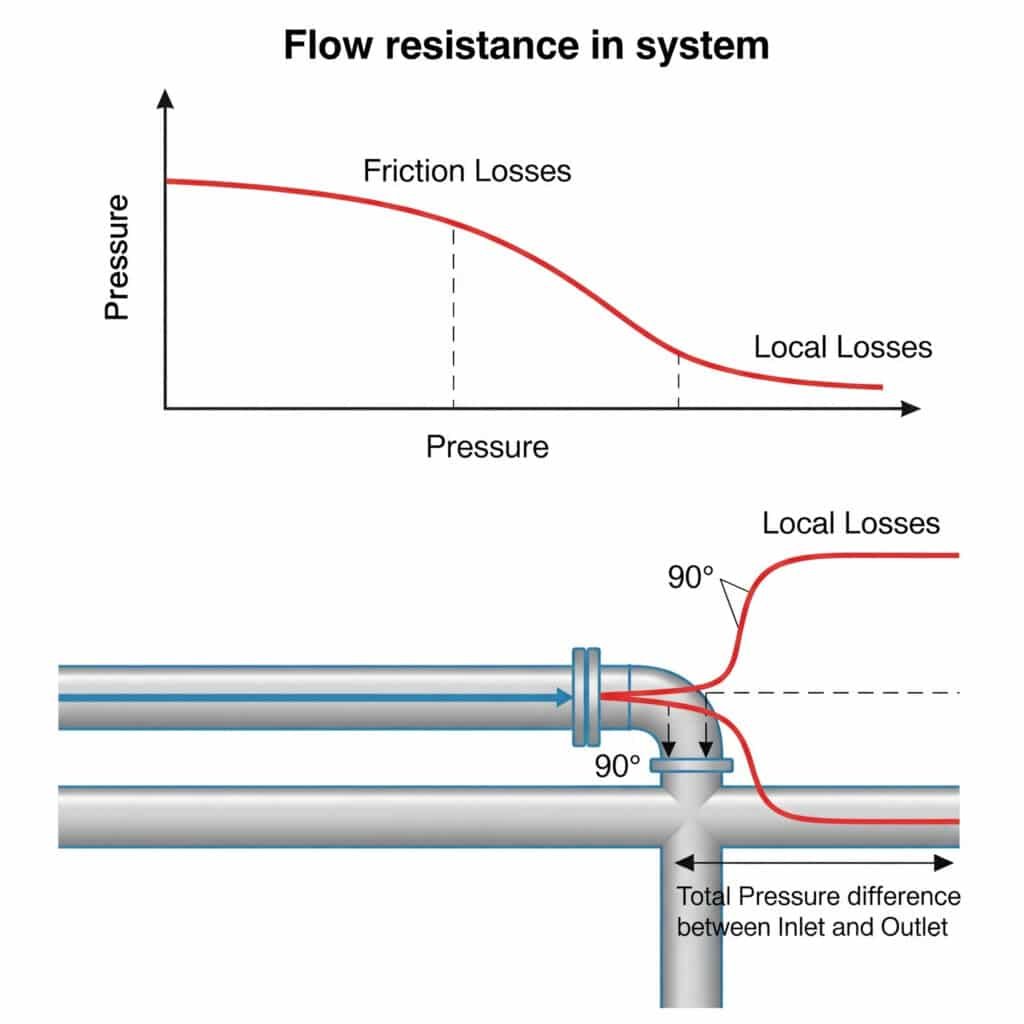
Η αντίσταση ροής στα πνευματικά συστήματα δημιουργεί πτώσεις πίεσης που μειώνουν τη διαθέσιμη δύναμη, περιορίζουν τη μέγιστη ταχύτητα και προκαλούν ασυνεχή κίνηση. Η αντίσταση αυτή προέρχεται τόσο από τριβές κατά μήκος ευθύγραμμων σωλήνων (απώλειες τριβής) όσο και από διαταραχές στα εξαρτήματα, τις καμπύλες και τις βαλβίδες (τοπικές απώλειες). Μαζί, αυτές οι αντιστάσεις μπορούν να μειώσουν την πραγματική απόδοση του συστήματος κατά 20-50% σε σύγκριση με τους θεωρητικούς υπολογισμούς.
Στα πάνω από 15 χρόνια που εργάζομαι στην Bepto με πνευματικά συστήματα, έχω δει αμέτρητες περιπτώσεις όπου η κατανόηση και η αντιμετώπιση της αντίστασης ροής έχει μετατρέψει συστήματα με χαμηλή απόδοση σε αξιόπιστες, αποδοτικές λειτουργίες. Επιτρέψτε μου να μοιραστώ όσα έχω μάθει σχετικά με τον υπολογισμό και την ελαχιστοποίηση αυτών των κρυφών δολοφόνων της απόδοσης.
Πίνακας περιεχομένων
- Πώς υπολογίζετε στην πραγματικότητα τις απώλειες τριβής σε πνευματικές γραμμές;
- Γιατί η μέθοδος ισοδύναμου μήκους είναι κρίσιμη για τον ακριβή σχεδιασμό συστημάτων;
- Τι συμβαίνει όταν ο αέρας ρέει μέσω τμημάτων μειωμένης οπής;
- Συμπέρασμα
- Συχνές ερωτήσεις σχετικά με την αντίσταση ροής σε πνευματικά συστήματα
Πώς υπολογίζετε στην πραγματικότητα τις απώλειες τριβής σε πνευματικές γραμμές;
Οι απώλειες τριβής σε ευθύγραμμους σωλήνες και σωληνάκια αποτελούν τη βάση των υπολογισμών της αντίστασης ροής, αλλά πολλοί μηχανικοί βασίζονται σε υπεραπλουστευμένους κανόνες που οδηγούν σε υποδιαστασιολογημένα συστήματα.
Οι απώλειες τριβής στις πνευματικές γραμμές υπολογίζονται με τη χρήση του Εξίσωση Darcy-Weisbach1: ΔP = λ(L/D)(ρv²/2), όπου λ είναι ο συντελεστής τριβής, L είναι το μήκος του σωλήνα, D είναι η διάμετρος του σωλήνα, ρ είναι η πυκνότητα του αέρα και v είναι η ταχύτητα ροής. Για τα πνευματικά συστήματα, ο συντελεστής τριβής λ μεταβάλλεται με βάση Αριθμός Reynolds2 και της σχετικής τραχύτητας, και συνήθως προσδιορίζεται με τη χρήση πινάκων αναζήτησης ή του Διάγραμμα Moody3.
Η κατανόηση των απωλειών τριβής έχει πρακτικές συνέπειες για το σχεδιασμό του συστήματος και την αντιμετώπιση προβλημάτων. Επιτρέψτε μου να το αναλύσω σε ιδέες που μπορούν να γίνουν πράξη.
Αποτελεσματική χρήση πινάκων συντελεστών τριβής
Ο συντελεστής τριβής (λ) είναι η βασική παράμετρος για τον υπολογισμό των πτώσεων πίεσης, αλλά ο προσδιορισμός της τιμής του απαιτεί την εξέταση των συνθηκών ροής:
| Καθεστώς ροής | Αριθμός Reynolds (Re) | Προσδιορισμός συντελεστή τριβής |
|---|---|---|
| Στρωτή ροή | Re < 2000 | λ = 64/Re |
| Μεταβατική ροή | 2000 < Re < 4000 | Αναξιόπιστο - αποφύγετε το σχεδιασμό σε αυτό το εύρος |
| Τυρβώδης ροή | Re > 4000 | Χρήση πινάκων αναζήτησης με βάση τη σχετική τραχύτητα (ε/D) |
Πρακτικός πίνακας αναζήτησης συντελεστή τριβής
Για τυρβώδη ροή σε πνευματικά συστήματα, χρησιμοποιήστε αυτόν τον απλουστευμένο πίνακα:
| Υλικό σωλήνα | Σχετική τραχύτητα (ε/D) | Συντελεστής τριβής (λ) σε κοινούς αριθμούς Reynolds |
|---|---|---|
| Re = 10.000 | ||
| Ομαλοί σωλήνες (PVC, πολυουρεθάνη) | 0.0001 – 0.0005 | 0.031 |
| Σωλήνας αλουμινίου | 0.001 – 0.002 | 0.035 |
| Γαλβανισμένος χάλυβας | 0.003 – 0.005 | 0.042 |
| Σκουριασμένος χάλυβας | 0.01 – 0.05 | 0.054 |
Υπολογισμός της πτώσης πίεσης σε πραγματικά πνευματικά συστήματα
Ας δούμε ένα πρακτικό παράδειγμα:
| Παράμετρος | Αξία/Υπολογισμός | Παράδειγμα |
|---|---|---|
| Διάμετρος σωλήνα (D) | Εσωτερική διάμετρος | 8mm (0.008m) |
| Μήκος σωλήνα (L) | Συνολικό ευθύγραμμο μήκος | 5m |
| Ρυθμός ροής (Q) | Από τις απαιτήσεις συστήματος | 20 τυποποιημένα λίτρα/δευτερόλεπτο |
| Πυκνότητα αέρα (ρ) | Σε πίεση λειτουργίας | 7,2 kg/m³ σε 6 bar |
| Ταχύτητα ροής (v) | v = Q/(π×D²/4) | v = 0,02m³/s/(π×0,008²/4) = 398 m/s |
| Αριθμός Reynolds (Re) | Re = ρvD/μ | Re = 7,2×398×0,008/1,8×10-⁵ = 1.273.600 |
| Σχετική τραχύτητα | Για σωλήνες πολυουρεθάνης | 0.0003 |
| Συντελεστής τριβής (λ) | Από τον πίνακα αναζήτησης | 0.017 |
| Πτώση πίεσης (ΔP) | ΔP = λ(L/D)(ρv²/2) | ΔP = 0,017×(5/0,008)×(7,2×398²/2) = 6,07 bar |
Πραγματική εφαρμογή: Ταχύτητα κυλίνδρου
Πέρυσι, συνεργάστηκα με τη Σάρα, μια μηχανικό παραγωγής σε μια εταιρεία εξοπλισμού συσκευασίας στο Ουισκόνσιν. Το σύστημα κυλίνδρων χωρίς ράβδο λειτουργούσε μόνο με 60% της αναμενόμενης ταχύτητας, παρά το γεγονός ότι διέθετε το σωστό μέγεθος κυλίνδρου και επαρκή πίεση τροφοδοσίας.
Αφού ανέλυσα το σύστημά της, ανακάλυψα ότι χρησιμοποιούσε σωλήνες 6 mm για μια εφαρμογή υψηλής ροής. Οι απώλειες τριβής προκαλούσαν πτώση πίεσης 2,1 bar, μειώνοντας σημαντικά τη διαθέσιμη δύναμη και ταχύτητα. Με την αναβάθμιση σε σωλήνες 10mm, μειώσαμε την πτώση πίεσης στα 0,4 bar και το σύστημά της πέτυχε αμέσως την απαιτούμενη απόδοση χωρίς άλλες αλλαγές.
Παράγοντες που επηρεάζουν τις απώλειες τριβής σε πραγματικά συστήματα
Διάφοροι παράγοντες επηρεάζουν τις πραγματικές απώλειες τριβής:
- Θερμοκρασία αέρα: Οι υψηλότερες θερμοκρασίες αυξάνουν το ιξώδες και την τριβή
- Μόλυνση: Η βρωμιά και το λάδι μπορούν να αυξήσουν την αποτελεσματική τραχύτητα
- Κάμψη σωλήνων: Η μικρο-παραμόρφωση στους λυγισμένους σωλήνες αυξάνει την αντίσταση
- Επιδείνωση της ηλικίας: Η διάβρωση και οι εναποθέσεις αυξάνουν την τραχύτητα με την πάροδο του χρόνου
- Πίεση λειτουργίας: Οι υψηλότερες πιέσεις αυξάνουν την πυκνότητα και τις απώλειες
Γιατί η μέθοδος ισοδύναμου μήκους είναι κρίσιμη για τον ακριβή σχεδιασμό συστημάτων;
Οι τοπικές απώλειες στα εξαρτήματα, τις βαλβίδες και τις καμπύλες συχνά υπερβαίνουν τις απώλειες τριβής στους ευθύγραμμους σωλήνες, αλλά πολλοί μηχανικοί είτε τις αγνοούν είτε χρησιμοποιούν χονδροειδείς μεθόδους εκτίμησης που οδηγούν σε προβλήματα απόδοσης.
Η μέθοδος ισοδύναμου μήκους μετατρέπει τις τοπικές απώλειες από εξαρτήματα και βαλβίδες σε ένα ισοδύναμο μήκος ευθύγραμμου σωλήνα που θα προκαλούσε την ίδια πτώση πίεσης. Αυτό υπολογίζεται με τη χρήση Le = K(D/λ), όπου Le είναι το ισοδύναμο μήκος, K είναι το τοπικός συντελεστής απωλειών4, D είναι η διάμετρος του σωλήνα και λ είναι ο συντελεστής τριβής. Η μέθοδος αυτή απλοποιεί τους υπολογισμούς και παρέχει ακριβέστερες προβλέψεις της απόδοσης του συστήματος.
Ας διερευνήσουμε πώς να εφαρμόσουμε αποτελεσματικά αυτή τη μέθοδο στο σχεδιασμό πνευματικών συστημάτων.
Πίνακες ισοδύναμου μήκους για κοινά πνευματικά εξαρτήματα
Ακολουθεί ένας πρακτικός πίνακας αναφοράς για τα κοινά πνευματικά εξαρτήματα:
| Στοιχείο | Τιμή Κ | Ισοδύναμο μήκος (Le/D) |
|---|---|---|
| Αγκώνας 90° (αιχμηρός) | 0.9 | 30 |
| Αγκώνας 90° (τυπική ακτίνα) | 0.3 | 10 |
| Αγκώνας 45° | 0.2 | 7 |
| Διασταύρωση Τ (διαμπερής ροή) | 0.3 | 10 |
| Διασταύρωση Τ (ροή διακλάδωσης) | 1.0 | 33 |
| Σφαιρική βαλβίδα (πλήρως ανοικτή) | 0.1 | 3 |
| Βαλβίδα πύλης (πλήρως ανοικτή) | 0.2 | 7 |
| Σύνδεσμος γρήγορης σύνδεσης | 0.4-0.8 | 13-27 |
| Βαλβίδα ελέγχου | 1.5-2.5 | 50-83 |
| Τυπική βαλβίδα ελέγχου ροής | 1.0-3.0 | 33-100 |
Εφαρμογή της μεθόδου ισοδύναμου μήκους
Για να χρησιμοποιήσετε αυτή τη μέθοδο αποτελεσματικά:
- Προσδιορίστε όλα τα εξαρτήματα του πνευματικού σας κυκλώματος
- Βρείτε την τιμή Κ ή τον ισοδύναμο λόγο μήκους (Le/D) για κάθε συστατικό.
- Υπολογίστε το ισοδύναμο μήκος πολλαπλασιάζοντας με τη διάμετρο του σωλήνα.
- Προσθέστε όλα τα ισοδύναμα μήκη στο πραγματικό μήκος του ευθύγραμμου σωλήνα
- Χρησιμοποιήστε το συνολικό ωφέλιμο μήκος στους υπολογισμούς σας για τις απώλειες τριβής.
Για παράδειγμα, ένα σύστημα με 5 μέτρα ευθύγραμμου σωλήνα 8 mm και τέσσερις γωνίες 90°, μία διακλάδωση Τ και δύο ταχυσυνδέσμους:
| Στοιχείο | Ποσότητα | Le/D | Ισοδύναμο μήκος |
|---|---|---|---|
| Γωνίες 90° | 4 | 10 | 4 × 10 × 0,008m = 0,32m |
| T-Junction | 1 | 10 | 1 × 10 × 0,008m = 0,08m |
| Γρήγορες συνδέσεις | 2 | 20 | 2 × 20 × 0,008m = 0,32m |
| Συνολικό ισοδύναμο μήκος | 0.72m | ||
| Πραγματικό ευθύγραμμο μήκος | 5.00m | ||
| Συνολικό αποτελεσματικό μήκος | 5.72m |
Αυτό σημαίνει ότι το σύστημα των 5 μέτρων συμπεριφέρεται στην πραγματικότητα σαν σύστημα 5,72 μέτρων λόγω των τοπικών απωλειών - μια αύξηση του πραγματικού μήκους κατά 14,4%.
Μελέτη περίπτωσης: Συστήματα συναρμολόγησης
Πρόσφατα βοήθησα τον Μιγκέλ, έναν μηχανικό αυτοματισμού σε ένα εργοστάσιο συναρμολόγησης ηλεκτρονικών ειδών στην Αριζόνα. Το σύστημα pick-and-place του παρουσίαζε ασυνεχείς διακυμάνσεις στην κίνηση και στον χρόνο κύκλου, παρά τη χρήση εξαρτημάτων υψηλής ποιότητας.
Η ανάλυση αποκάλυψε ότι ο συλλέκτης βαλβίδων βρισκόταν 3 μέτρα μακριά από τους κυλίνδρους και το κύκλωμα περιλάμβανε πολλά εξαρτήματα. Ο υπολογισμός του ισοδύναμου μήκους έδειξε ότι η πραγματική απόσταση των 3m είχε πραγματικό μήκος 7,2m λόγω των τοπικών απωλειών - περισσότερο από το διπλάσιο της απόστασης με ευθεία σωλήνα!
Με τη μετατόπιση του συλλέκτη βαλβίδων πιο κοντά στους κυλίνδρους και την εξάλειψη αρκετών εξαρτημάτων, μειώσαμε το πραγματικό μήκος από 7,2 σε 2,1 μέτρα. Αυτό μείωσε την πτώση πίεσης κατά 70%, με αποτέλεσμα σταθερή κίνηση και μείωση του χρόνου κύκλου κατά 15%.
Πρακτικές συμβουλές για την ελαχιστοποίηση των τοπικών απωλειών
Για να μειώσετε τις τοπικές απώλειες στα πνευματικά σας συστήματα:
- Χρησιμοποιήστε σαρώδεις ή στρογγυλεμένους αγκώνες αντί για απότομες στροφές (μειώνει την τιμή Κ κατά 67%)
- Ελαχιστοποίηση του αριθμού των εξαρτημάτων σχεδιάζοντας πιο άμεση δρομολόγηση
- Επιλέξτε εξαρτήματα χαμηλής συστολής όπως οι σφαιρικές βαλβίδες πλήρους διαμέτρου, όπου ενδείκνυται
- Σωστό μέγεθος εξαρτημάτων - τα υποδιαστασιολογημένα εξαρτήματα προκαλούν δυσανάλογες απώλειες
- Τοποθετήστε τις βαλβίδες κοντά στους ενεργοποιητές για την ελαχιστοποίηση του πραγματικού μήκους των σωλήνων
Τι συμβαίνει όταν ο αέρας ρέει μέσω τμημάτων μειωμένης οπής;
Οι μειωμένες διατομές σε πνευματικά κυκλώματα -όπως οι μερικώς κλειστές βαλβίδες, τα υποδιαστασιολογημένα εξαρτήματα ή οι μεταβάσεις διαμέτρου- δημιουργούν σημαντικούς περιορισμούς ροής που μπορούν να επηρεάσουν σοβαρά την απόδοση του συστήματος.
Όταν ο αέρας ρέει μέσω μειωμένων διατομών, Πτώσεις πίεσης5 συμβαίνουν σύμφωνα με τον τύπο ΔP = ρ(v₂² - v₁²)/2, όπου v₁ είναι η ταχύτητα πριν από τον περιορισμό και v₂ είναι η ταχύτητα στον περιορισμό. Αυτό μπορεί να αντισταθμιστεί με τη χρήση του συντελεστή αντιστάθμισης του λόγου διάτρησης C = (1 - (d/D)⁴), όπου d είναι η μειωμένη διάμετρος και D η αρχική διάμετρος. Αυτός ο παράγοντας βοηθά στην πρόβλεψη της πραγματικής απόδοσης του συστήματος και στην αποφυγή υποδιαστασιολόγησης των εξαρτημάτων.
Ας διερευνήσουμε τις πρακτικές επιπτώσεις των μειωμένων διατομών και πώς να τις λάβουμε υπόψη μας στο σχεδιασμό του συστήματος.
Υπολογισμός των σταγόνων πίεσης στις μεταβάσεις διαμέτρου
Όταν ο αέρας ρέει από μια μεγαλύτερη διάμετρο σε μια μικρότερη, η πτώση πίεσης μπορεί να υπολογιστεί χρησιμοποιώντας:
| Παράμετρος | Φόρμουλα | Παράδειγμα |
|---|---|---|
| Αρχική διάμετρος (D) | Από τις προδιαγραφές | 10mm |
| Μειωμένη διάμετρος (d) | Από τις προδιαγραφές | 6mm |
| Αναλογία οπών (d/D) | Απλή διαίρεση | 0.6 |
| Ρυθμός ροής (Q) | Από τις απαιτήσεις συστήματος | 15 τυποποιημένα λίτρα/δευτερόλεπτο |
| Ταχύτητα στον αρχικό σωλήνα (v₁) | v₁ = Q/(π×D²/4) | 191 m/s |
| Ταχύτητα στο μειωμένο τμήμα (v₂) | v₂ = Q/(π×d²/4) | 531 m/s |
| Πτώση πίεσης (ΔP) | ΔP = ρ(v₂² - v₁²)/2 | 0,88 bar |
| Συντελεστής αντιστάθμισης (C) | C = (1 - (d/D)⁴) | 0.87 |
Συνήθη σενάρια μείωσης της οπής και ο αντίκτυπός τους
Ακολουθεί ο τρόπος με τον οποίο οι διαφορετικές μειώσεις οπών επηρεάζουν τη χωρητικότητα ροής:
| Μείωση οπών | Μείωση χωρητικότητας ροής | Αύξηση της πτώσης πίεσης |
|---|---|---|
| 10mm έως 8mm | 36% | 2.4× |
| 10mm έως 6mm | 64% | 7.7× |
| 10mm έως 4mm | 84% | 39× |
| 8mm έως 6mm | 44% | 3.2× |
| 8mm έως 4mm | 75% | 16× |
| 6mm έως 4mm | 56% | 5.1× |
Αυτοί οι αριθμοί υπογραμμίζουν γιατί φαινομενικά μικρές μειώσεις στη διάμετρο μπορούν να έχουν δραματικές επιπτώσεις στην απόδοση του συστήματος.
Το σωρευτικό αποτέλεσμα των πολλαπλών περιορισμών
Στα πραγματικά πνευματικά κυκλώματα, εμφανίζονται πολλαπλοί περιορισμοί σε σειρά. Η επίδρασή τους είναι αθροιστική και μπορεί να υπολογιστεί χρησιμοποιώντας:
- Μετατροπή κάθε περιορισμού στον ισοδύναμο συντελεστή C
- Υπολογίστε τον συνολικό συντελεστή C: Ctotal = 1 - (1-C₁)(1-C₂)(1-C₃)...
- Χρησιμοποιήστε αυτόν τον συνολικό συντελεστή για να προσδιορίσετε τη συνολική μείωση της απόδοσης του συστήματος.
Μελέτη περίπτωσης: Ενεργοποιητή: Επίλυση προβλημάτων αναντιστοιχίας βαλβίδας-ενεργοποιητή
Τον περασμένο μήνα, συνεργάστηκα με τον Thomas, έναν υπεύθυνο συντήρησης σε ένα εργοστάσιο κατασκευής επίπλων στη Βόρεια Καρολίνα. Το νέο του σύστημα κυλίνδρων χωρίς ράβδο λειτουργούσε σε λιγότερο από το μισό της αναμενόμενης ταχύτητας, παρά τη χρήση του συνιστώμενου από τον κατασκευαστή μεγέθους βαλβίδας.
Η έρευνα αποκάλυψε πολλαπλές μειώσεις οπών στο κύκλωμά του:
- Γραμμή τροφοδοσίας 10 mm σε θύρες βαλβίδας 8 mm (C₁ = 0,36)
- Θύρες βαλβίδας 8 mm σε εξαρτήματα 6 mm (C₂ = 0,44)
- Εξαρτήματα 6mm σε θυρίδες κυλίνδρου 8mm με εσωτερικούς περιορισμούς (C₃ = 0,32)
Ο συνολικός συντελεστής αντιστάθμισης ήταν Ctotal = 1 - (1-0,36)(1-0,44)(1-0,32) = 0,75, που σημαίνει ότι το σύστημά του έχανε 75% της θεωρητικής του ικανότητας ροής!
Με την αναβάθμιση σε εξαρτήματα κατάλληλου μεγέθους σε όλο το σύστημα, εξαλείψαμε αυτούς τους περιορισμούς και επιτύχαμε την απαιτούμενη απόδοση χωρίς να αλλάξουμε τον κύλινδρο ή την πίεση τροφοδοσίας.
Πρακτικές στρατηγικές για την ελαχιστοποίηση των απωλειών μείωσης της οπής
Για να μειωθούν οι απώλειες από μειώσεις οπών:
- Μέγεθος εξαρτημάτων με συνέπεια σε όλο το πνευματικό κύκλωμα
- Χρησιμοποιήστε το μεγαλύτερο πρακτικό μέγεθος σωλήνων για εφαρμογές υψηλής ροής
- Δώστε προσοχή στους περιορισμούς των εσωτερικών εξαρτημάτων, όχι μόνο μεγέθη σύνδεσης
- Εξετάστε παράλληλες διαδρομές ροής για απαιτήσεις υψηλής ροής
- Εξάλειψη περιττών προσαρμογέων και μεταβάσεων όπου είναι δυνατόν
Η αρχή του "ασθενέστερου κρίκου" στα πνευματικά συστήματα
Να θυμάστε ότι η απόδοση του πνευματικού σας συστήματος περιορίζεται από το πιο περιοριστικό στοιχείο του. Ένα μεμονωμένο στοιχείο με υποδιαστασιολόγηση μπορεί να ακυρώσει τα οφέλη των σωστά διαστασιολογημένων εξαρτημάτων σε άλλα σημεία του συστήματος.
Για παράδειγμα, ένα σύστημα με σωληνώσεις 10mm, βαλβίδες 10mm, αλλά εξαρτήματα 6mm στον κύλινδρο θα έχει ουσιαστικά την ίδια απόδοση με ένα σύστημα με εξαρτήματα 6mm σε όλο το μήκος του - με υψηλότερο κόστος.
Συμπέρασμα
Η κατανόηση και ο σωστός υπολογισμός της αντίστασης ροής -μέσω πινάκων συντελεστών τριβής, μεθόδων ισοδύναμου μήκους και αντιστάθμισης μειωμένης διάτρησης- είναι απαραίτητη για το σχεδιασμό πνευματικών συστημάτων που αποδίδουν όπως αναμένεται σε πραγματικές συνθήκες. Με την εφαρμογή αυτών των μεθόδων υπολογισμού και των αρχών σχεδιασμού, μπορείτε να βελτιστοποιήσετε τις εφαρμογές των κυλίνδρων χωρίς ράβδο και άλλων πνευματικών συστημάτων για μέγιστη απόδοση και αξιοπιστία.
Συχνές ερωτήσεις σχετικά με την αντίσταση ροής σε πνευματικά συστήματα
Πόση πτώση πίεσης είναι αποδεκτή σε ένα πνευματικό σύστημα;
Η αποδεκτή πτώση πίεσης εξαρτάται από τις απαιτήσεις της εφαρμογής σας, αλλά ως γενική οδηγία, περιορίστε τη συνολική πτώση πίεσης σε 10-15% της πίεσης τροφοδοσίας για αποδοτική λειτουργία. Για ένα σύστημα 6 bar, αυτό σημαίνει ότι η συνολική πτώση πίεσης πρέπει να είναι κάτω από 0,6-0,9 bar. Οι κρίσιμες εφαρμογές ενδέχεται να απαιτούν ακόμη χαμηλότερες πτώσεις πίεσης 5-8% για να διατηρηθεί σταθερή απόδοση.
Ποια είναι η σχέση μεταξύ της διαμέτρου του σωλήνα και της πτώσης πίεσης;
Η πτώση πίεσης είναι αντιστρόφως ανάλογη της πέμπτης δύναμης της διαμέτρου (D⁵) για τυρβώδη ροή σε πνευματικά συστήματα. Αυτό σημαίνει ότι ο διπλασιασμός της διαμέτρου του σωλήνα μειώνει την πτώση πίεσης κατά περίπου 32 φορές. Για παράδειγμα, η αύξηση από 6mm σε 12mm σωλήνων μπορεί να μειώσει την πτώση πίεσης από 1,5 bar σε μόλις 0,047 bar υπό τις ίδιες συνθήκες ροής.
Πώς μπορώ να προσδιορίσω το σωστό μέγεθος σωλήνα για την πνευματική μου εφαρμογή;
Επιλέξτε το μέγεθος του σωλήνα με βάση τις απαιτήσεις της παροχής και την αποδεκτή πτώση πίεσης. Υπολογίστε τον αριθμό Reynolds και τον συντελεστή τριβής και, στη συνέχεια, χρησιμοποιήστε την εξίσωση Darcy-Weisbach για να προσδιορίσετε την πτώση πίεσης για διαφορετικές διαμέτρους. Επιλέξτε τη μικρότερη διάμετρο που διατηρεί την πτώση πίεσης εντός αποδεκτών ορίων (συνήθως <10% της πίεσης τροφοδοσίας), λαμβάνοντας υπόψη τους περιορισμούς χώρου και το κόστος.
Τι δημιουργεί μεγαλύτερο περιορισμό: ένας αγκώνας 90° ή 5 μέτρα ευθύγραμμου σωλήνα;
Ένας αιχμηρός αγκώνας 90° δημιουργεί συνήθως αντίσταση ισοδύναμη με 30 διαμέτρους σωλήνων ευθείας σωλήνωσης. Για σωλήνες 8mm, ένας αιχμηρός γωνιακός ισοδυναμεί με περίπου 240mm (30 × 8mm) ευθύγραμμου σωλήνα. Αυτό σημαίνει ότι 5 μέτρα ευθύγραμμου σωλήνα δημιουργούν περίπου 21 φορές μεγαλύτερο περιορισμό από έναν απλό αγκώνα. Ωστόσο, τα συστήματα συχνά περιέχουν πολλαπλούς αγκώνες και εξαρτήματα, των οποίων η αθροιστική επίδραση μπορεί να υπερβαίνει τις απώλειες ευθύγραμμου μήκους.
Πώς επηρεάζουν τα εξαρτήματα ταχείας σύνδεσης την απόδοση του συστήματος;
Τα τυποποιημένα εξαρτήματα ταχείας σύνδεσης εισάγουν συνήθως τοπικές απώλειες ισοδύναμες με 15-25 διαμέτρους σωλήνων ευθείας σωλήνωσης. Πιο σημαντικά, πολλά εξαρτήματα ταχείας σύνδεσης έχουν εσωτερικούς περιορισμούς μικρότερους από το ονομαστικό τους μέγεθος. Ένας ταχυσύνδεσμος "10mm" μπορεί να έχει εσωτερικό περιορισμό μόνο 7-8mm, δημιουργώντας μείωση της οπής που μπορεί να μειώσει τη χωρητικότητα ροής κατά 50-70% σε εκείνο το σημείο.
Ποιος είναι ο αντίκτυπος των μερικώς κλειστών βαλβίδων ελέγχου ροής στην απόδοση του συστήματος;
Μια βαλβίδα ελέγχου ροής κλειστή στα 50% της πλήρους επιφάνειας του διαφράγματός της δεν μειώνει τη ροή μόνο κατά 50% - μειώνει τη ροή κατά περίπου 75% λόγω της μη γραμμικής σχέσης μεταξύ διαμέτρου και χωρητικότητας ροής. Η πτώση πίεσης αυξάνεται σύμφωνα με το τετράγωνο της μεταβολής της ταχύτητας, οπότε η μείωση της πραγματικής διαμέτρου στο μισό αυξάνει την πτώση πίεσης κατά περίπου 16 φορές υπό τις ίδιες συνθήκες ροής.
-
Παρέχει μια λεπτομερή ανάλυση της εξίσωσης Darcy-Weisbach, ενός θεμελιώδους και ευρέως χρησιμοποιούμενου τύπου στη δυναμική των ρευστών για τον υπολογισμό της απώλειας πίεσης λόγω τριβής σε έναν σωλήνα. ↩
-
Προσφέρει έναν σαφή ορισμό του αριθμού Reynolds, ενός κρίσιμου μεγέθους χωρίς διαστάσεις που χρησιμοποιείται για την πρόβλεψη των προτύπων ροής (στρωτή ή τυρβώδης) σε διάφορες καταστάσεις ροής ρευστών. ↩
-
Παρουσιάζει το διάγραμμα Moody, ένα ολοκληρωμένο γράφημα που απεικονίζει τον συντελεστή τριβής Darcy συναρτήσει του αριθμού Reynolds και της σχετικής τραχύτητας, το οποίο αποτελεί το τυπικό εργαλείο για τους μηχανικούς για τον προσδιορισμό της πτώσης πίεσης σε σωλήνες. ↩
-
Εξηγεί την έννοια της τιμής Κ ή του συντελεστή τοπικών απωλειών, ενός αριθμού χωρίς διαστάσεις που χρησιμοποιείται για να χαρακτηρίσει την απώλεια πίεσης σε ένα εξάρτημα σωλήνα ή μια βαλβίδα ως μέρος της μεθόδου ισοδύναμου μήκους. ↩
-
Αναλύει λεπτομερώς τη φυσική πίσω από την πτώση πίεσης που εμφανίζεται όταν ένα ρευστό διέρχεται από έναν περιορισμό (ένα στόμιο), με βάση τις αρχές της εξίσωσης συνέχειας και της αρχής του Bernoulli. ↩



