
Αντιμετωπίζετε ασυνεχείς ταχύτητες πνευματικών κυλίνδρων ή απροσδόκητα χτυπήματα στο τέλος της διαδρομής; Αυτά τα κοινά προβλήματα συχνά οφείλονται σε κακή κατανόηση της κινηματικής του εμβόλου. Πολλοί μηχανικοί επικεντρώνονται αποκλειστικά στις απαιτήσεις δύναμης, ενώ παραβλέπουν τις κρίσιμες παραμέτρους κίνησης που καθορίζουν την απόδοση του συστήματος.
Κινηματική του εμβόλου1 επηρεάζουν άμεσα την απόδοση του πνευματικού συστήματος μέσω των σχέσεων πίεσης-ταχύτητας, των ορίων επιτάχυνσης και των απαιτήσεων απορρόφησης. Η κατανόηση αυτών των αρχών επιτρέπει στους μηχανικούς να διαστασιολογούν σωστά τα εξαρτήματα, να προβλέπουν τα πραγματικά προφίλ κίνησης και να αποτρέπουν τις πρόωρες αστοχίες σε κυλίνδρους χωρίς ράβδο και άλλους πνευματικούς ενεργοποιητές.
Στα 15+ χρόνια που εργάζομαι στην Bepto με πνευματικά συστήματα, έχω δει αμέτρητες περιπτώσεις όπου η κατανόηση αυτών των θεμελιωδών αρχών βοήθησε τους πελάτες να λύσουν επίμονα προβλήματα απόδοσης και να παρατείνουν τη διάρκεια ζωής του εξοπλισμού κατά 3-5 φορές.
Πίνακας περιεχομένων
- Τι πίεση χρειάζεστε πραγματικά για κίνηση σταθερής ταχύτητας;
- Πώς υπολογίζεται η μέγιστη δυνατή επιτάχυνση σε πνευματικούς κυλίνδρους;
- Γιατί έχει σημασία ο χρόνος αναστολής και πώς υπολογίζεται;
- Συμπέρασμα
- Συχνές ερωτήσεις σχετικά με την κινηματική των εμβόλων στα πνευματικά συστήματα
Τι πίεση χρειάζεστε πραγματικά για κίνηση σταθερής ταχύτητας;
Πολλοί μηχανικοί απλώς εφαρμόζουν τη μέγιστη διαθέσιμη πίεση στα πνευματικά τους συστήματα, αλλά αυτή η προσέγγιση είναι αναποτελεσματική και μπορεί να οδηγήσει σε σπασμωδικές κινήσεις, υπερβολική φθορά και σπατάλη ενέργειας.
Η πίεση που απαιτείται για την κίνηση σταθερής ταχύτητας σε έναν πνευματικό κύλινδρο υπολογίζεται χρησιμοποιώντας P = (F + Fr)/A, όπου P είναι η πίεση, F είναι η εξωτερική δύναμη φορτίου, Fr είναι η αντίσταση τριβής και A είναι η επιφάνεια του εμβόλου. Αυτός ο υπολογισμός εξασφαλίζει ομαλή, αποτελεσματική λειτουργία χωρίς υπερβολική πίεση που σπαταλά ενέργεια και επιταχύνει τη φθορά των εξαρτημάτων.
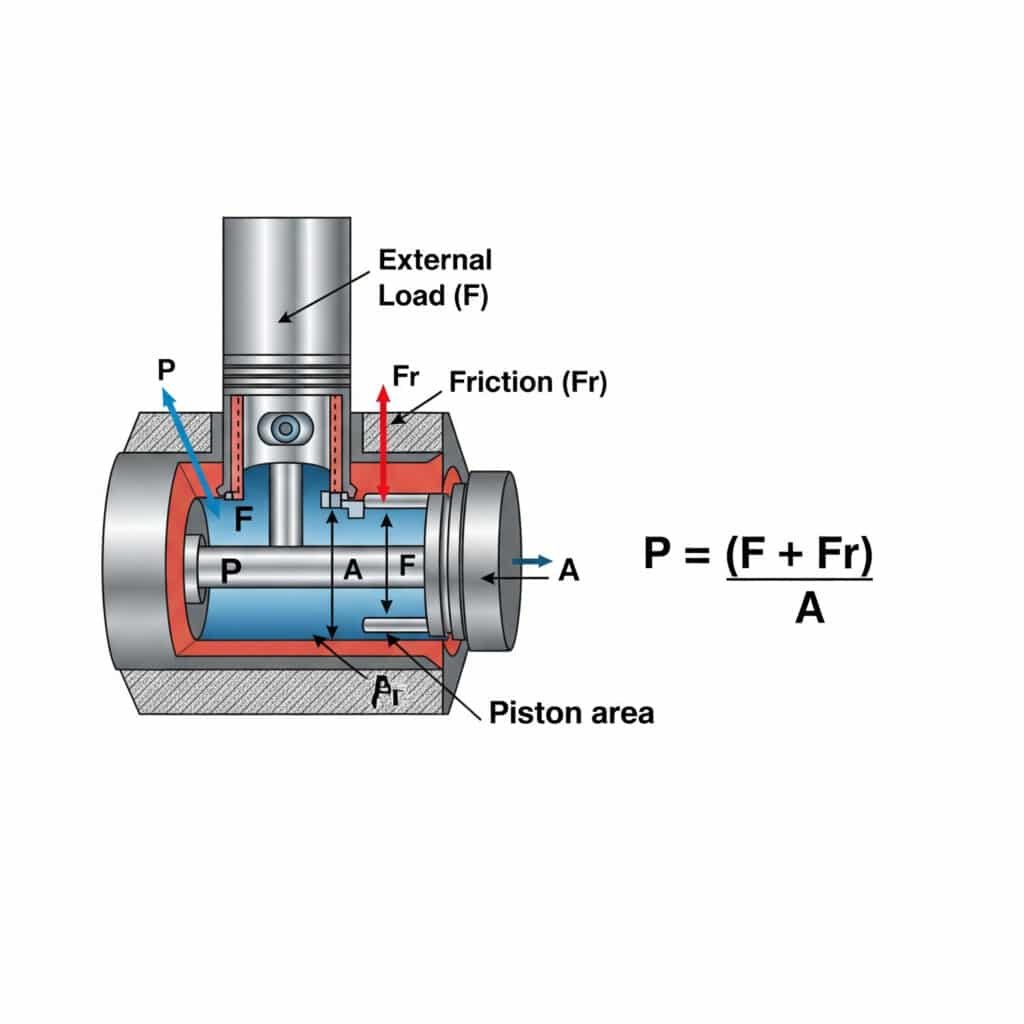
Η κατανόηση των απαιτήσεων πίεσης για κίνηση σταθερής ταχύτητας έχει πρακτικές επιπτώσεις στο σχεδιασμό και τη λειτουργία του συστήματος. Επιτρέψτε μου να το αναλύσω σε ιδέες που μπορούν να γίνουν πράξη.
Παράγοντες που επηρεάζουν τις απαιτήσεις πίεσης για σταθερή ταχύτητα
Η πίεση που απαιτείται για τη διατήρηση σταθερής ταχύτητας εξαρτάται από διάφορους παράγοντες:
| Παράγοντας | Επίδραση στην απαίτηση πίεσης | Πρακτικός προβληματισμός |
|---|---|---|
| Εξωτερικό φορτίο | Άμεση γραμμική σχέση | Διαφέρει ανάλογα με τον προσανατολισμό και τις εξωτερικές δυνάμεις |
| Τριβή | Προσθέτει στην απαιτούμενη πίεση | Αλλαγές με τη φθορά της φλάντζας και τη λίπανση |
| Περιοχή εμβόλου | Αντιστρόφως ανάλογη | Μεγαλύτερη διάτρηση = χαμηλότερη απαίτηση πίεσης |
| Περιορισμοί παροχής αέρα | Πτώσεις πίεσης σε γραμμές/βαλβίδες | Μέγεθος εξαρτημάτων για ελάχιστη πτώση πίεσης |
| Αντίστροφη πίεση | Αντιτίθεται στην πρόταση | Εξετάστε την ικανότητα ροής καυσαερίων |
Υπολογισμός της ελάχιστης πίεσης για σταθερή κίνηση
Για τον προσδιορισμό της ελάχιστης πίεσης που απαιτείται για σταθερή κίνηση:
- Υπολογίστε τη δύναμη που απαιτείται για να ξεπεραστεί το εξωτερικό φορτίο
- Προσθέστε τη δύναμη τριβής (συνήθως 3-20% της μέγιστης δύναμης).
- Διαιρέστε με την πραγματική επιφάνεια του εμβόλου
- Προσθέστε έναν παράγοντα σταθερότητας (συνήθως 10-30%)
Για παράδειγμα, σε έναν κύλινδρο χωρίς ράβδο διαμέτρου 40 mm με φορτίο 10 kg και τριβή 15%:
| Παράμετρος | Υπολογισμός | Αποτέλεσμα |
|---|---|---|
| Φορτίο Δύναμη | 10kg × 9,81m/s² | 98.1N |
| Δύναμη τριβής | 15% μέγιστης δύναμης σε 6 bar | ~45N |
| Συνολική δύναμη | 98.1N + 45N | 143.1N |
| Περιοχή εμβόλου | π × (0,02m)² | 0.00126m² |
| Ελάχιστη πίεση | 143,1N ÷ 0,00126m² | 113.571 Pa (1,14 bar) |
| Με συντελεστή σταθερότητας 20% | 1,14 bar × 1,2 | 1,37 bar |
Πραγματική εφαρμογή: Εξοικονόμηση ενέργειας μέσω βελτιστοποίησης της πίεσης
Πέρυσι, συνεργάστηκα με τον Robert, έναν μηχανικό παραγωγής σε ένα εργοστάσιο κατασκευής επίπλων στο Μίσιγκαν. Η αυτοματοποιημένη γραμμή συναρμολόγησης που χρησιμοποιούσε χρησιμοποιούσε κυλίνδρους χωρίς ράβδους που λειτουργούσαν στην πλήρη πίεση τροφοδοσίας των 6 bar, ανεξάρτητα από το φορτίο.
Αφού αναλύσαμε την εφαρμογή του, διαπιστώσαμε ότι οι περισσότερες κινήσεις απαιτούν μόνο 2,5-3 bar για σταθερή λειτουργία. Με την εγκατάσταση αναλογικοί ρυθμιστές πίεσης, μειώσαμε την κατανάλωση αέρα κατά 40% διατηρώντας τον ίδιο χρόνο κύκλου. Με τον τρόπο αυτό εξοικονομήθηκαν περίπου $12.000 ετησίως σε κόστος ενέργειας, ενώ παράλληλα μειώθηκε η φθορά των σφραγίδων και παρατάθηκαν τα διαστήματα συντήρησης.
Σχέση ταχύτητας-πίεσης σε πραγματικά συστήματα
Στην πράξη, η σχέση μεταξύ πίεσης και ταχύτητας δεν είναι απόλυτα γραμμική λόγω:
- Περιορισμοί ροής: Η διαστασιολόγηση των βαλβίδων και των θυρίδων επηρεάζει τη μέγιστη επιτεύξιμη ταχύτητα
- Επιδράσεις συμπιεστότητας: Ο αέρας είναι συμπιέσιμος, προκαλώντας υστέρηση στην επιτάχυνση
- Φαινόμενα stick-slip: Τα χαρακτηριστικά τριβής αλλάζουν με την ταχύτητα
- Αδρανειακές επιδράσεις: Η επιτάχυνση της μάζας απαιτεί πρόσθετη δύναμη/πίεση
Πώς υπολογίζεται η μέγιστη δυνατή επιτάχυνση σε πνευματικούς κυλίνδρους;
Η κατανόηση των ορίων επιτάχυνσης είναι ζωτικής σημασίας για την πρόληψη υπερβολικών κραδασμών, δονήσεων και πρόωρης βλάβης εξαρτημάτων σε πνευματικά συστήματα.
Η μέγιστη δυνατή επιτάχυνση σε έναν πνευματικό κύλινδρο υπολογίζεται χρησιμοποιώντας a = (P × A - F - Fr)/m, όπου a είναι η επιτάχυνση, P είναι η πίεση, A είναι η επιφάνεια του εμβόλου, F είναι το εξωτερικό φορτίο, Fr είναι η αντίσταση τριβής και m είναι η κινούμενη μάζα. Αυτή η εξίσωση ορίζει τα φυσικά όρια του πόσο γρήγορα μπορεί να ξεκινήσει ή να σταματήσει την κίνηση ένας πνευματικός ενεργοποιητής.
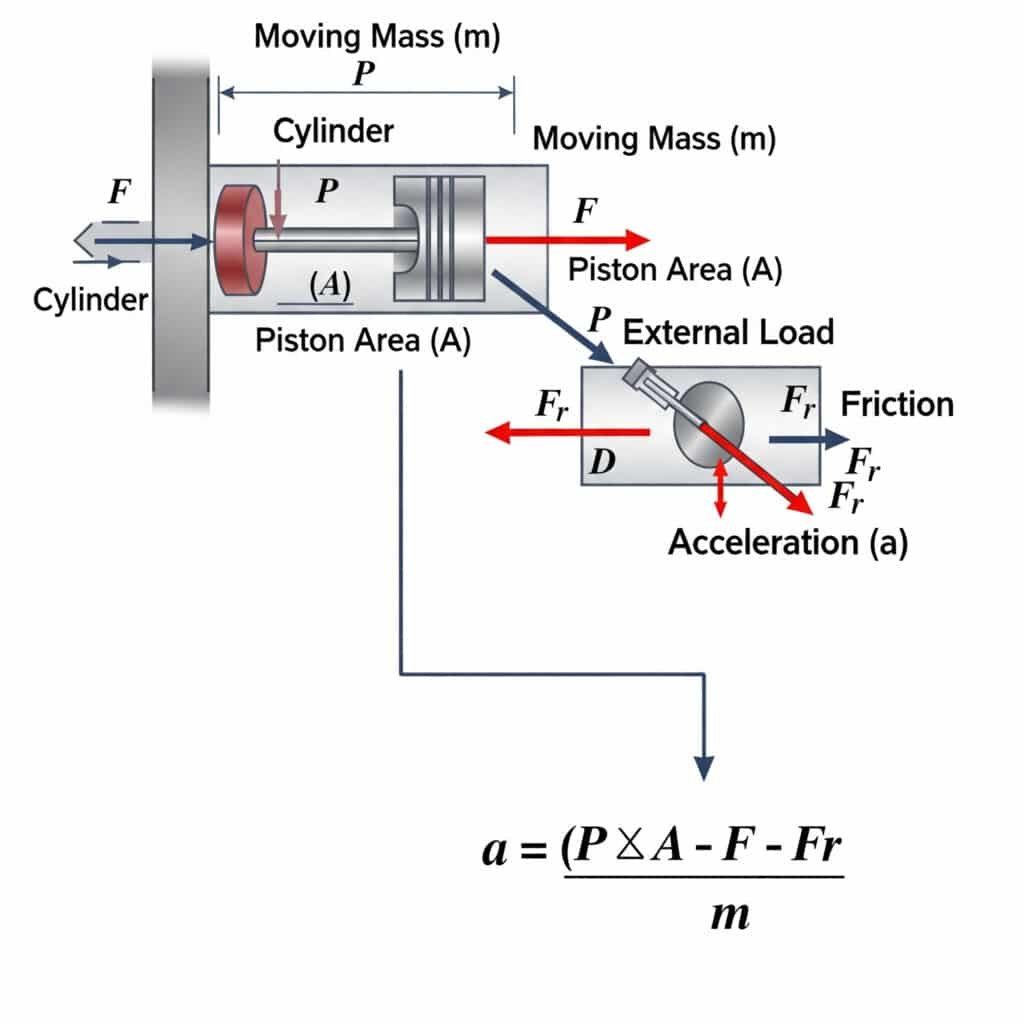
Τα θεωρητικά όρια επιτάχυνσης έχουν σημαντικές πρακτικές συνέπειες για το σχεδιασμό του συστήματος και την επιλογή εξαρτημάτων.
Παραγωγή της οριακής εξίσωσης επιτάχυνσης
Η εξίσωση του ορίου επιτάχυνσης προέρχεται από Ο δεύτερος νόμος του Νεύτωνα2 (F = ma):
- Η καθαρή δύναμη που είναι διαθέσιμη για επιτάχυνση είναι: Fnet = Fpressure - Fload - Ffriction
- Fpressure = P × A
- Επομένως: a = Fnet/m = (P × A - F - Fr)/m
Πρακτικά όρια επιτάχυνσης για διαφορετικούς τύπους κυλίνδρων
Διαφορετικά σχέδια κυλίνδρων έχουν διαφορετικά πρακτικά όρια επιτάχυνσης:
| Τύπος κυλίνδρου | Τυπική μέγιστη επιτάχυνση | Περιοριστικοί παράγοντες |
|---|---|---|
| Τυποποιημένος κύλινδρος ράβδου | 10-15 m/s² | Λυγισμός ράβδου, φορτία έδρασης |
| Κύλινδρος χωρίς ράβδο (μαγνητικός) | 8-12 m/s² | Ισχύς μαγνητικής σύζευξης |
| Κύλινδρος χωρίς ράβδο (μηχανικός) | 15-25 m/s² | Σχεδιασμός στεγανοποίησης/ έδρασης, εσωτερική τριβή |
| Κύλινδρος οδηγός | 20-30 m/s² | Ακαμψία συστήματος οδηγού, φέρουσα ικανότητα |
| Κύλινδρος κρούσης | 50-100+ m/s² | Ειδικά σχεδιασμένο για υψηλή επιτάχυνση |
Εκτιμήσεις μάζας στους υπολογισμούς επιτάχυνσης
Κατά τον υπολογισμό της επιτάχυνσης, είναι σημαντικό να συμπεριλάβετε όλες τις κινούμενες μάζες:
- Συγκρότημα εμβόλου: Περιλαμβάνει το έμβολο, τις τσιμούχες και τα στοιχεία σύνδεσης
- Μάζα φορτίου: Εξωτερικό φορτίο που μετακινείται
- Αποτελεσματική μάζα κινούμενου αέρα: Συχνά αμελητέος, αλλά σχετικός σε εφαρμογές υψηλής ταχύτητας
- Προστιθέμενη μάζα λόγω εξαρτημάτων τοποθέτησης: Βάσεις, αισθητήρες κ.λπ.
Κάποτε βοήθησα έναν πελάτη στη Γαλλία, ο οποίος αντιμετώπιζε μυστηριώδεις βλάβες στο σύστημα κυλίνδρων χωρίς ράβδο. Ο κύλινδρος ήταν σωστά διαστασιολογημένος για το αναφερόμενο φορτίο των 15kg, αλλά παρουσίαζε συνεχή βλάβη μετά από μερικές χιλιάδες κύκλους.
Μετά από έρευνα, ανακαλύψαμε ότι είχε παραλείψει να υπολογίσει τη μάζα των 12 κιλών της πλάκας στήριξης και των εξαρτημάτων. Η πραγματική κινούμενη μάζα ήταν σχεδόν διπλάσια από αυτήν που είχε υπολογίσει, προκαλώντας δυνάμεις επιτάχυνσης που ξεπερνούσαν τα όρια σχεδιασμού του κυλίνδρου. Μετά την αναβάθμιση σε μεγαλύτερο κύλινδρο, οι βλάβες σταμάτησαν εντελώς.
Μέθοδοι ελέγχου επιτάχυνσης
Για τον έλεγχο της επιτάχυνσης εντός ασφαλών ορίων:
- Βαλβίδες ελέγχου ροής: Περιορισμός της ροής κατά την αρχική κίνηση
- Αναλογικές βαλβίδες: Παροχή ελεγχόμενης αύξησης της πίεσης
- Επιτάχυνση πολλαπλών σταδίων: Χρησιμοποιήστε κλιμακωτές αυξήσεις πίεσης
- Μηχανική απόσβεση: Προσθέστε εξωτερικά αμορτισέρ
- Ηλεκτρονικός έλεγχος: Χρήση σερβο-πνευματικά συστήματα3 με ανατροφοδότηση επιτάχυνσης
Γιατί έχει σημασία ο χρόνος αναστολής και πώς υπολογίζεται;
Η σωστή απορρόφηση του τέλους της διαδρομής είναι απαραίτητη για την αποφυγή ζημιών από χτυπήματα, τη μείωση του θορύβου και την παράταση της διάρκειας ζωής των πνευματικών κυλίνδρων. Η κατανόηση του χρόνου απορρόφησης βοηθά τους μηχανικούς να σχεδιάζουν συστήματα που εξισορροπούν τον χρόνο κύκλου με τη μακροζωία των εξαρτημάτων.
Ο χρόνος απορρόφησης στους πνευματικούς κυλίνδρους υπολογίζεται με τη χρήση της εξίσωσης t = √(2s/a), όπου t είναι ο χρόνος, s είναι το μήκος της διαδρομής απορρόφησης και a είναι η επιβράδυνση. Ο χρόνος αυτός αντιπροσωπεύει το χρονικό διάστημα που απαιτείται για την ασφαλή επιβράδυνση της κινούμενης μάζας πριν από την πρόσκρουση, η οποία είναι κρίσιμη για την αποφυγή ζημιών στον κύλινδρο και στα προσαρτημένα εξαρτήματα.

Ας εξερευνήσουμε τις πρακτικές πτυχές των υπολογισμών του χρόνου απορρόφησης και τις επιπτώσεις τους στο σχεδιασμό του συστήματος.
Η φυσική πίσω από την πνευματική απορρόφηση
Πνευματικό μαξιλάρι λειτουργεί μέσω ελεγχόμενης συμπίεσης του αέρα και περιορισμένης εξάτμισης:
- Καθώς το έμβολο εισέρχεται στο θάλαμο μαξιλαριού, η διαδρομή της εξάτμισης περιορίζεται
- Ο παγιδευμένος αέρας συμπιέζεται, δημιουργώντας αυξανόμενη αντίθλιψη
- Αυτή η αντίθλιψη δημιουργεί μια αντίρροπη δύναμη που επιβραδύνει το έμβολο
- Το προφίλ επιβράδυνσης εξαρτάται από το σχεδιασμό και τη ρύθμιση του μαξιλαριού.
Υπολογισμός του βέλτιστου χρόνου απορρόφησης
Ο βέλτιστος χρόνος απορρόφησης εξισορροπεί την πρόληψη των κρούσεων με την αποδοτικότητα του χρόνου κύκλου:
| Παράμετρος | Φόρμουλα | Παράδειγμα |
|---|---|---|
| Απόσταση απορρόφησης | Με βάση τον σχεδιασμό του κυλίνδρου | 15mm (τυπικό για διάτρηση 40mm) |
| Απαιτούμενη επιβράδυνση | a = v²/(2s) | Για v=0,5m/s, s=15mm: a = 8,33m/s² |
| Χρόνος απορρόφησης | t = √(2s/a) | t = √(2×0,015/8,33) = 0,06s |
| Συσσώρευση πίεσης | P = P₀(V₀/V)^γ | Εξαρτάται από τη γεωμετρία του θαλάμου μαξιλαριού |
Παράγοντες που επηρεάζουν την απόδοση της απορρόφησης
Διάφοροι παράγοντες επηρεάζουν την πραγματική απόδοση της αντικραδασμικής προστασίας:
- Σχεδιασμός σφραγίδας μαξιλαριού: Επηρεάζει τη διαρροή αέρα κατά την αντικραδασμική προστασία
- Ρύθμιση βαλβίδας βελόνας: Ελέγχει το ποσοστό περιορισμού της εξάτμισης
- Κινούμενη μάζα: Τα βαρύτερα φορτία απαιτούν μεγαλύτερο χρόνο απορρόφησης
- Ταχύτητα προσέγγισης: Υψηλότερες ταχύτητες απαιτούν μεγαλύτερη απόσταση μαξιλαριού
- Πίεση λειτουργίας: Επηρεάζει τη μέγιστη διαθέσιμη αντίρροπη δύναμη
Τύποι μαξιλαριών και οι εφαρμογές τους
Διαφορετικοί μηχανισμοί απορρόφησης είναι κατάλληλοι για διαφορετικές εφαρμογές:
| Τύπος μαξιλαριού | Χαρακτηριστικά | Καλύτερες εφαρμογές |
|---|---|---|
| Σταθερή απορρόφηση | Απλό, μη ρυθμιζόμενο | Ελαφρά φορτία, συνεπής λειτουργία |
| Ρυθμιζόμενο μαξιλάρι | Ρυθμιζόμενο με βαλβίδες βελόνας | Μεταβαλλόμενα φορτία, ευέλικτες εφαρμογές |
| Αυτορρυθμιζόμενο μαξιλάρι | Προσαρμόζεται σε διαφορετικές συνθήκες | Αλλαγή ταχυτήτων και φορτίων |
| Εξωτερικά αμορτισέρ | Υψηλή απορρόφηση ενέργειας | Βαριά φορτία, υψηλές ταχύτητες |
| Ηλεκτρονικό μαξιλάρι | Ακριβώς ελεγχόμενη επιβράδυνση | Σερβο-πνευματικά συστήματα |
Μελέτη περίπτωσης: Εφαρμογές υψηλού κύκλου λειτουργίας
Πρόσφατα συνεργάστηκα με τον Thomas, έναν μηχανικό σχεδιασμού σε έναν κατασκευαστή εξαρτημάτων αυτοκινήτων στη Γερμανία. Η γραμμή συναρμολόγησης που χρησιμοποιούσε χρησιμοποιούσε κυλίνδρους χωρίς ράβδο που λειτουργούσαν με 45 κύκλους ανά λεπτό, αλλά αντιμετώπιζε συχνές αστοχίες στεγανοποίησης και ζημιές στο βραχίονα τοποθέτησης.
Η ανάλυση αποκάλυψε ότι ο χρόνος απορρόφησης ήταν πολύ μικρός για την κινούμενη μάζα, προκαλώντας δυνάμεις κρούσης σχεδόν 3G σε κάθε άκρο της διαδρομής. Με την αύξηση της διαδρομής απορρόφησης από 12mm σε 20mm και τη βελτιστοποίηση των ρυθμίσεων της βαλβίδας βελόνας, επεκτείναμε το χρόνο απορρόφησης από 0,04s σε 0,07s.
Αυτή η φαινομενικά μικρή αλλαγή μείωσε τις δυνάμεις κρούσης κατά πάνω από 60%, εξάλειψε εντελώς τη ζημιά στο βραχίονα και επέκτεινε τη διάρκεια ζωής της στεγανοποίησης από 3 μήνες σε πάνω από ένα έτος - και όλα αυτά διατηρώντας τον απαιτούμενο χρόνο κύκλου.
Πρακτική διαδικασία ρύθμισης μαξιλαριών
Για βέλτιστη απόδοση απορρόφησης σε κυλίνδρους χωρίς ράβδο:
- Ξεκινήστε με τις βαλβίδες μαξιλαριού πλήρως ανοικτές (ελάχιστος περιορισμός)
- Κλείστε σταδιακά τη βαλβίδα του μαξιλαριού μέχρι να επιτευχθεί ομαλή επιβράδυνση.
- Δοκιμή με ελάχιστα και μέγιστα αναμενόμενα φορτία
- Επαληθεύστε την απόδοση της αντικραδασμικής προστασίας σε όλο το εύρος ταχυτήτων
- Ακούστε για ήχους πρόσκρουσης που υποδεικνύουν ανεπαρκή αντικραδασμική προστασία
- Μετρήστε τον πραγματικό χρόνο επιβράδυνσης για να επιβεβαιώσετε τους υπολογισμούς
Συμπέρασμα
Η κατανόηση των αρχών της κινηματικής των εμβόλων - από τις απαιτήσεις πίεσης για σταθερή ταχύτητα έως τα όρια επιτάχυνσης και τους υπολογισμούς του χρόνου απορρόφησης - είναι απαραίτητη για τον σχεδιασμό αποδοτικών και αξιόπιστων πνευματικών συστημάτων. Εφαρμόζοντας αυτές τις αρχές στις εφαρμογές σας με κυλίνδρους χωρίς ράβδο, μπορείτε να βελτιστοποιήσετε την απόδοση, να μειώσετε την κατανάλωση ενέργειας και να παρατείνετε σημαντικά τη διάρκεια ζωής των εξαρτημάτων.
Συχνές ερωτήσεις σχετικά με την κινηματική των εμβόλων στα πνευματικά συστήματα
Τι πίεση χρειάζομαι για μια συγκεκριμένη ταχύτητα κυλίνδρου;
Η απαιτούμενη πίεση εξαρτάται από το φορτίο, την τριβή και την επιφάνεια του κυλίνδρου. Υπολογίστε την χρησιμοποιώντας P = (F + Fr)/A, όπου F είναι η δύναμη του εξωτερικού φορτίου, Fr είναι η αντίσταση τριβής και A είναι η επιφάνεια του εμβόλου. Για έναν τυπικό κύλινδρο χωρίς ράβδο που κινεί οριζόντια ένα φορτίο 10 kg, θα χρειαστείτε περίπου 1,5-2 bar για σταθερή κίνηση σε μέτριες ταχύτητες.
Πόσο γρήγορα μπορεί να επιταχύνει ένας πνευματικός κύλινδρος;
Η μέγιστη επιτάχυνση ενός πνευματικού κυλίνδρου υπολογίζεται χρησιμοποιώντας a = (P × A - F - Fr)/m. Οι τυπικοί κύλινδροι χωρίς ράβδο μπορούν να επιτύχουν επιτάχυνση 10-25 m/s² ανάλογα με τον σχεδιασμό. Αυτό μεταφράζεται σε επίτευξη ταχύτητας 0,5 m/s σε περίπου 20-50 χιλιοστά του δευτερολέπτου υπό βέλτιστες συνθήκες.
Ποιοι παράγοντες περιορίζουν τη μέγιστη ταχύτητα ενός κυλίνδρου χωρίς ράβδο;
Η μέγιστη ταχύτητα περιορίζεται από την ικανότητα ροής της βαλβίδας, τον όγκο παροχής αέρα, τη διαστασιολόγηση των θυρίδων, τις δυνατότητες απορρόφησης και το σχεδιασμό της στεγανοποίησης. Οι περισσότεροι τυποποιημένοι κύλινδροι χωρίς ράβδο είναι σχεδιασμένοι για μέγιστες ταχύτητες 0,8-1,5 m/s, αν και οι εξειδικευμένοι σχεδιασμοί υψηλής ταχύτητας μπορούν να φτάσουν τα 2-3 m/s.
Πώς μπορώ να υπολογίσω την κατάλληλη απορρόφηση για την εφαρμογή μου;
Υπολογίστε την κατάλληλη απορρόφηση προσδιορίζοντας την κινητική ενέργεια (KE = ½mv²) του κινούμενου φορτίου σας και εξασφαλίζοντας ότι το σύστημα απορρόφησης μπορεί να απορροφήσει αυτή την ενέργεια. Ο χρόνος απορρόφησης πρέπει να υπολογίζεται χρησιμοποιώντας t = √(2s/a), όπου s είναι η απόσταση απορρόφησης και a είναι ο επιθυμητός ρυθμός επιβράδυνσης.
Τι συμβαίνει αν ο πνευματικός μου κύλινδρος επιταχύνει πολύ γρήγορα;
Η υπερβολική επιτάχυνση μπορεί να προκαλέσει μηχανική καταπόνηση στα εξαρτήματα στερέωσης, πρόωρη φθορά των στεγανοποιητικών, αυξημένους κραδασμούς και θόρυβο, πιθανή μετατόπιση ή βλάβη του φορτίου και μειωμένη ακρίβεια του συστήματος. Μπορεί επίσης να οδηγήσει σε σπασμωδικές κινήσεις που επηρεάζουν την ποιότητα των προϊόντων σε εφαρμογές ακριβείας.
Πώς επηρεάζει ο προσανατολισμός του φορτίου την πίεση που απαιτείται για την κίνηση;
Ο προσανατολισμός του φορτίου επηρεάζει σημαντικά τις απαιτήσεις πίεσης. Τα κατακόρυφα φορτία που κινούνται ενάντια στη βαρύτητα απαιτούν πρόσθετη πίεση για να ξεπεραστεί η βαρυτική δύναμη (P = F/A + Fg/A + Fr/A). Τα οριζόντια φορτία πρέπει να υπερνικήσουν μόνο την τριβή και την αδράνεια. Τα κεκλιμένα φορτία βρίσκονται μεταξύ αυτών των άκρων με βάση το ημίτονο της γωνίας.
-
Παρέχει μια θεμελιώδη εξήγηση της κινηματικής, του κλάδου της μηχανικής που περιγράφει την κίνηση των αντικειμένων χωρίς να εξετάζει τις δυνάμεις που προκαλούν την κίνηση.
ηλεκτρονικό σήμα εισόδου, επιτρέποντας προηγμένο πνευματικό έλεγχο. ↩ -
Αναλυτικά ο δεύτερος νόμος του Νεύτωνα (F=ma), η θεμελιώδης αρχή της φυσικής που συσχετίζει τη δύναμη που ασκείται σε ένα αντικείμενο με τη μάζα και την επιτάχυνσή του, η οποία αποτελεί τη βάση για όλους τους δυναμικούς υπολογισμούς. ↩
-
Περιγράφει τη σερβο-πνευματική, μια προηγμένη τεχνολογία ελέγχου που συνδυάζει τη δύναμη της πνευματικής με την ακρίβεια του ηλεκτρονικού ελέγχου κλειστού βρόχου για την επίτευξη εξαιρετικά ακριβών προφίλ τοποθέτησης και κίνησης. ↩



