Kuidas mõjutab kolvi kinemaatika teie pneumaatilise süsteemi jõudlust?

CQ2 seeria kompaktsete pneumaatiliste silindrite koostekomplektid

Kas teil on probleeme ebaühtlase pneumosilindri kiiruse või ootamatute löökide lõppemisega? Need sagedased probleemid tulenevad sageli kolvi kinemaatika puudulikust mõistmisest. Paljud insenerid keskenduvad ainult jõunõuetele, jättes tähelepanuta kriitilised liikumisparameetrid, mis määravad süsteemi jõudluse.

Kolvi kinemaatika¹ mõjutavad otseselt pneumaatilise süsteemi toimivust rõhu ja kiiruse suhte, kiirenduspiiride ja pehmendusnõuete kaudu. Nende põhimõtete mõistmine võimaldab inseneridel õigesti dimensioneerida komponente, prognoosida tegelikke liikumisprofiile ja vältida varajasi rikkeid vardata silindrites ja muudes pneumaatilistes ajamites.

Enam kui 15 aasta jooksul, mil ma olen Beptos töötanud pneumaatiliste süsteemidega, olen näinud lugematul hulgal juhtumeid, kus nende aluspõhimõtete mõistmine on aidanud klientidel lahendada püsivaid jõudlusprobleeme ja pikendada seadmete kasutusiga 3-5 korda.

Sisukord

Millist rõhku on tegelikult vaja konstantse kiiruse liikumiseks?
Kuidas arvutada maksimaalset võimalikku kiirendust pneumaatilistes silindrites?
Miks on pehmendusaeg oluline ja kuidas seda arvutatakse?
Kokkuvõte
Korduma kippuvad küsimused kolvikinemaatika kohta pneumaatilistes süsteemides

Millist rõhku on tegelikult vaja konstantse kiiruse liikumiseks?

Paljud insenerid rakendavad pneumaatikasüsteemidele lihtsalt maksimaalset olemasolevat rõhku, kuid selline lähenemine on ebaefektiivne ja võib põhjustada hüppelist liikumist, liigset kulumist ja energia raiskamist.

Pneumosilindri konstantse kiirusega liikumiseks vajalik rõhk arvutatakse valemiga P = (F + Fr)/A, kus P on rõhk, F on väline koormusjõud, Fr on hõõrdetakistus ja A on kolvi pindala. See arvutus tagab sujuva ja tõhusa töö ilma liigse rõhuta, mis raiskab energiat ja kiirendab komponentide kulumist.

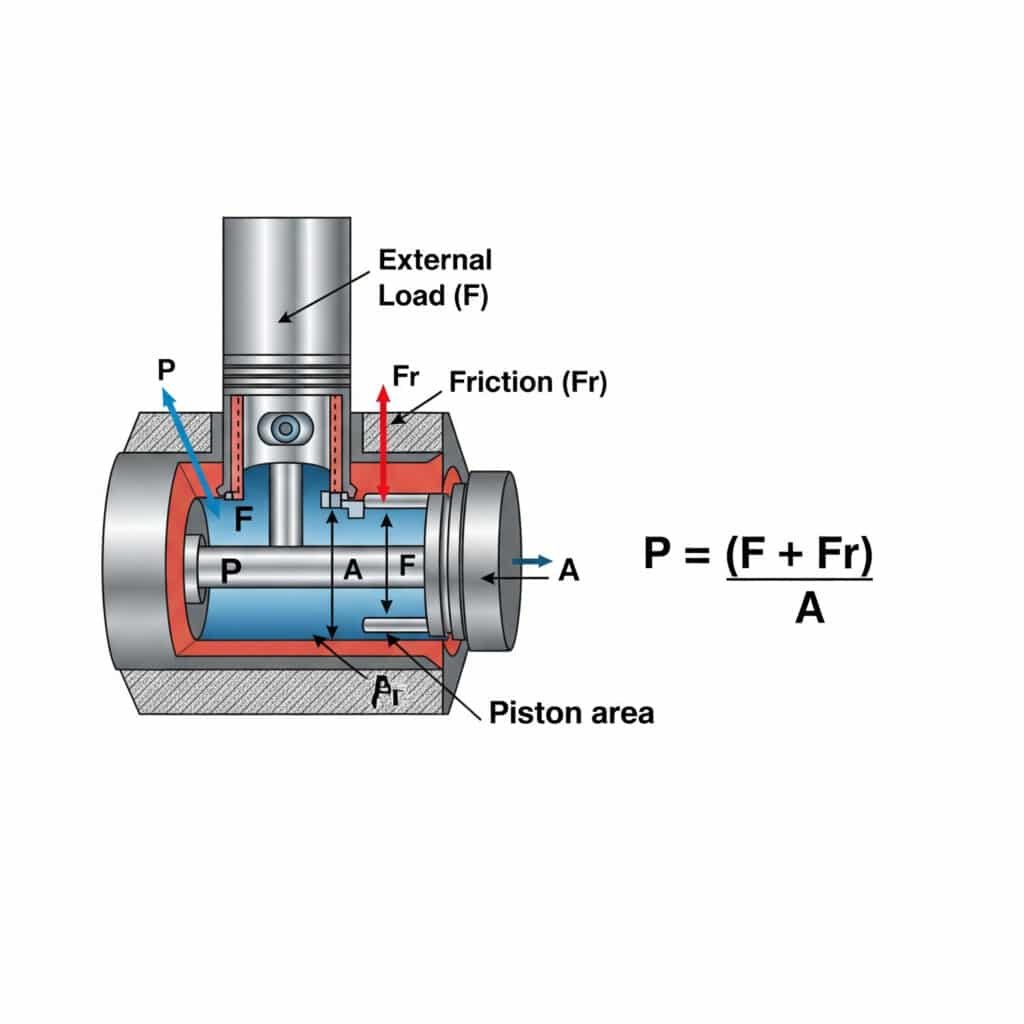
Tehniline vaba keha skeem, mis selgitab pneumosilindri rõhu arvutamist. Sellel on kujutatud plokki suruva silindri ristlõige, mis on tähistatud märkega "Väliskoormus (F)". Noolega on tähistatud vastassuunaline hõõrdumine (Fr). Sisemine rõhk on tähistatud "P" ja see mõjub kolbipinnale (A). Valem "P = (F + Fr)/A" on esitatud silmatorkavalt, kusjuures nooled ühendavad iga muutujat vastava jõu või omadusega diagrammil. — Konstantse kiiruse rõhu arvutusdiagramm

Pideva kiirusega liikumise rõhunõuete mõistmisel on praktiline mõju süsteemi projekteerimisele ja toimimisele. Lubage mul jagada see käepäraseks arusaamiseks.

Konstantse kiiruse rõhunõudeid mõjutavad tegurid

Konstantse kiiruse säilitamiseks vajalik surve sõltub mitmest tegurist:

Tegur	Mõju rõhunõudlusele	Praktilised kaalutlused
Väline koormus	Otsene lineaarne seos	Varieerub sõltuvalt orientatsioonist ja välistest jõududest
Hõõrdumine	Lisab nõutavat survet	Muutused seoses tihendite kulumise ja määrimisega
Kolvi pindala	Vastupidiselt proportsionaalne	Suurem avaus = väiksem rõhunõue
Õhuvarustuse piirangud	Rõhu langus liinides/ventiilides	Komponentide suurus minimaalse rõhulanguse saavutamiseks
Tagasirõhk	Vastustab ettepanekut	Arvestada heitgaasivoolu võimsust

Minimaalse rõhu arvutamine stabiilse liikumise jaoks

Et määrata kindlaks minimaalne surve, mis on vajalik stabiilseks liikumiseks:

Arvutage välise koormuse ületamiseks vajalik jõud.
Lisage hõõrdejõud (tavaliselt 3-20% maksimaalsest jõust).
Jagage efektiivse kolbipinnaga
Lisatakse stabiilsustegur (tavaliselt 10-30%).

Näiteks 40 mm läbimõõduga vardata silindri puhul, mille koormus on 10 kg ja hõõrdumine 15%:

Parameeter	Arvutus	Tulemus
Koormuse jõud	10kg × 9,81m/s²	98.1N
Hõõrdejõud	15% maksimaalne jõud 6 baari juures	~45N
Kogu jõud	98,1N + 45N	143.1N
Kolvi pindala	π × (0,02m)²	0.00126m²
Minimaalne rõhk	143,1N ÷ 0,00126m²	113,571 Pa (1,14 baari)
Koos 20% stabiilsusteguriga	1,14 bar × 1,2	1,37 baari

Reaalse maailma rakendus: Energia kokkuhoid rõhu optimeerimise kaudu

Eelmisel aastal töötasin koos Robertiga, kes oli tootmisinsener ühes Michigani mööblitootmisettevõttes. Tema automatiseeritud koosteliinil kasutati varraseta balloone, mis töötasid koormusest sõltumata täies 6 baari toiterõhu juures.

Pärast tema rakenduse analüüsimist leidsime, et enamik liikumisi nõuab stabiilseks toimimiseks vaid 2,5-3 baari. Paigaldades proportsionaalsed rõhuregulaatorid, vähendasime õhukulu 40% võrra, säilitades samasuguse tsükli kestuse. See säästis aastas ligikaudu $12 000 energiakulu, vähendades samal ajal tihendite kulumist ja pikendades hooldusintervalle.

Kiiruse ja rõhu suhe reaalsetes süsteemides

Praktikas ei ole rõhu ja kiiruse vaheline seos täiesti lineaarne, sest:

Voolupiirangud: Klapi ja ava mõõtmed mõjutavad maksimaalset saavutatavat kiirust.
Kokkupressiivsuse mõju: Õhk on kokkusurutav, põhjustades kiirenduse hilinemist.
Stick-slip nähtused: Hõõrdumisomadused muutuvad koos kiirusega
Inertsiaalsed mõjud: Massi kiirendamine nõuab täiendavat jõudu/rõhku

Kuidas arvutada maksimaalset võimalikku kiirendust pneumaatilistes silindrites?

Kiirenduspiiride mõistmine on oluline, et vältida pneumaatiliste süsteemide liigseid põrutusi, vibratsiooni ja komponentide enneaegset rikkeid.

Pneumosilindri maksimaalne võimalik kiirendus arvutatakse, kasutades a = (P × A - F - Fr)/m, kus a on kiirendus, P on rõhk, A on kolvi pindala, F on väline koormus, Fr on hõõrdetakistus ja m on liikuv mass. See võrrand määratleb füüsikalised piirid sellele, kui kiiresti pneumaatiline ajam saab liikumist alustada või peatada.

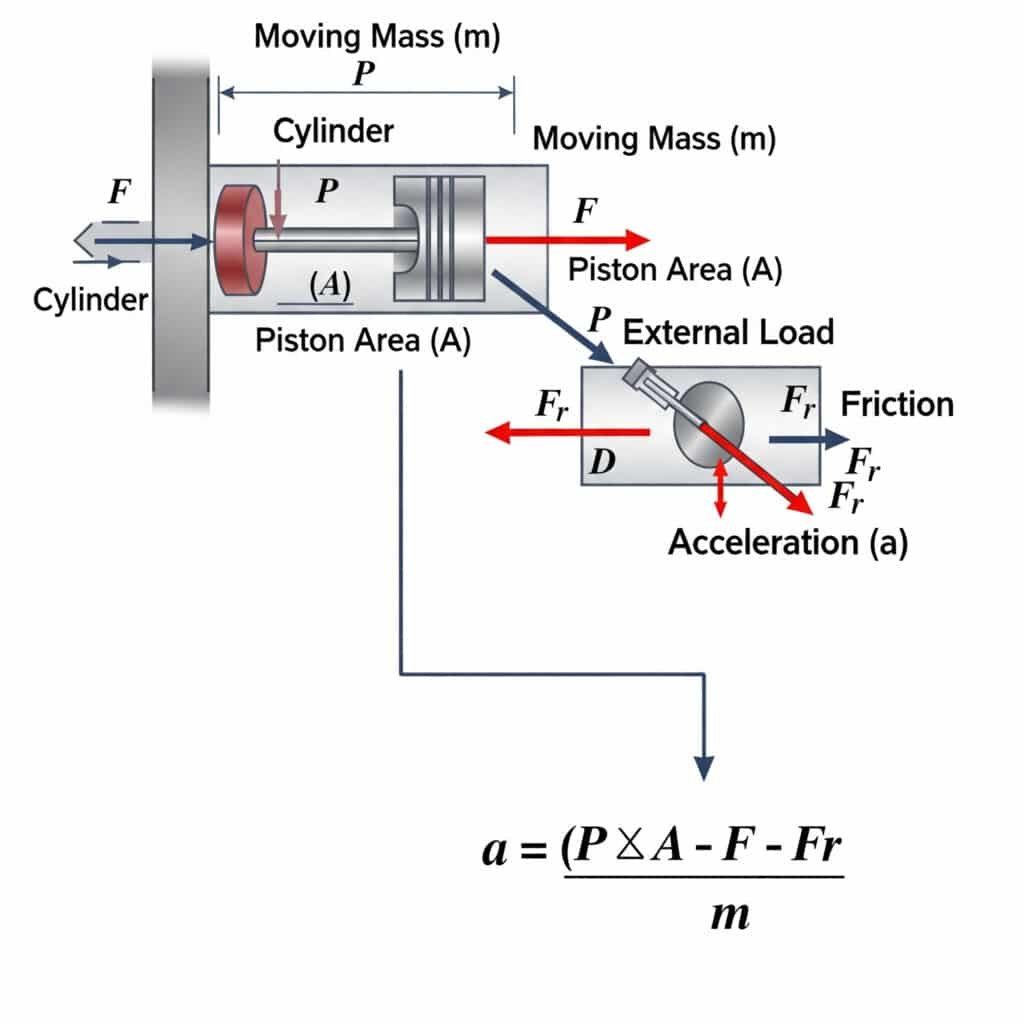
Tehniline vaba keha skeem, mis selgitab pneumosilindri kiirenduse arvutamist. Joonisel on kujutatud silinder, mis lükkab plokki, millel on tähis "Liikuv mass (m)". Suur nool tähistab liikumapanevat jõudu, mida tekitab 'Rõhk (P)' 'Kolbipinnale (A)'. Sellele vastanduvad kaks väiksemat noolt, millel on tähised "Väline koormus (F)" ja "Hõõrdumine (Fr)". Suur nool näitab sellest tulenevat kiirendust (a). Valem "a = (P × A - F - Fr)/m" on silmatorkavalt esitatud, kusjuures iga muutuja on seotud vastava elemendiga diagrammil. — Kiirenduse piirväärtuse tuletamise skeem

Teoreetilistel kiirenduspiiridel on märkimisväärne praktiline mõju süsteemi projekteerimisele ja komponentide valikule.

Kiirenduse piirvõrrandi tuletamine

Kiirenduse piirväärtuse võrrand pärineb Newtoni teine seadus² (F = ma):

Kiirendamiseks kasutatav netojõud on: Fnet = Fpressure - Fload - Ffriction
Frõhk = P × A
Seega: a = Fnet/m = (P × A - F - Fr)/m

Praktilised kiirenduspiirid erinevate silindertüüpide puhul

Erinevatel silindrite konstruktsioonidel on erinevad praktilised kiirenduspiirid:

Silindri tüüp	Tüüpiline maksimaalne kiirendus	Piirangulised tegurid
Standardne vardasilinder	10-15 m/s²	Varraste paindumine, laagrikoormused
Vardata silinder (magnetiline)	8-12 m/s²	Magnetilise sideme tugevus
Vardata silinder (mehaaniline)	15-25 m/s²	Tihendi/laagri konstruktsioon, sisemine hõõrdumine
Juhtsilinder	20-30 m/s²	Juhtimissüsteemi jäikus, kandevõime
Löögisilinder	50-100+ m/s²	Spetsiaalselt suure kiirenduse jaoks kavandatud

Massiga seotud kaalutlused kiirendusarvutustes

Kiirenduse arvutamisel on oluline kaasata kõik liikuvad massid:

Kolvi kokkupanek: Sisaldab kolbi, tihendid ja ühenduselemendid.
Koormuse mass: Väline koormus, mida liigutatakse
Liikuva õhu efektiivne mass: Sageli tähtsusetu, kuid oluline kiirrakenduste puhul.
Paigalduskomponentidest tingitud lisamass: Konsoolid, andurid jne.

Aitasin kord Prantsusmaal üht klienti, kellel esinesid salapärased tõrked tema vardata silindrisüsteemis. Silinder oli õigesti dimensioneeritud märgitud 15 kg koormuse jaoks, kuid pärast paari tuhandet tsüklit oli see pidevalt välja kukkunud.

Pärast uurimist avastasime, et ta oli unustanud arvestada paigaldusplaadi ja kinnituste 12 kg massiga. Tegelik liikuv mass oli peaaegu kaks korda suurem, kui ta oli arvutanud, põhjustades kiirendusjõude, mis ületasid silindri projekteerimispiirid. Pärast suurema silindri kasutuselevõttu lakkasid rikked täielikult.

Kiirenduse kontrollimise meetodid

Kiirenduse kontrollimiseks ohututes piirides:

Voolu reguleerimisventiilid: Voolukiiruse piiramine esialgse liikumise ajal
Proportsionaalsed ventiilid: Tagada kontrollitud rõhu tõstmine
Mitmeastmeline kiirendus: Kasutage astmelist rõhu tõusu
Mehaaniline summutus: Lisage välised amortisaatorid
Elektrooniline juhtimine: Kasutage servo-pneumaatilised süsteemid³ kiirenduse tagasisidega

Miks on pehmendusaeg oluline ja kuidas seda arvutatakse?

Takti lõpu korralik pehmendamine on oluline löögikahjustuste vältimiseks, müra vähendamiseks ja pneumosilindrite eluea pikendamiseks. Pehmendusaja mõistmine aitab inseneridel projekteerida süsteeme, mis tasakaalustavad tsükliaeg ja komponentide pikaealisus.

Pneumosilindrite pehmendusaeg arvutatakse võrrandi t = √(2s/a) abil, kus t on aeg, s on pehmendushoobi pikkus ja a on aeglustus. See aeg näitab, kui palju aega kulub liikuva massi ohutuks aeglustamiseks enne kokkupõrget, mis on kriitiline, et vältida silindri ja selle külge kinnitatud osade kahjustusi.

Tehniline infograafika, mis selgitab pneumaatilise pehmendusaja arvutamist. Sellel on kujutatud suurendatud ristlõige kolbist, mis siseneb pehmendusse silindri lõpus. Mõõtjoon tähistab "Pehmendushoogu (s)", samas kui suur vastanduv nool tähistab "aeglustust (a)". Stoppkella ikoon visualiseerib pehmendusaega (t). Valem "t = √(2s/a)" on silmatorkavalt kujutatud, kusjuures nooled ühendavad iga muutujat vastava elemendiga diagrammil. — Kiirenduse piirväärtuse tuletamise skeem

Uurime pehmendusaja arvutuste praktilisi aspekte ja nende mõju süsteemi projekteerimisele.

Pneumaatilise pehmenduse taga olev füüsika

Pneumaatiline pehmendus töötab kontrollitud õhu kokkusurumise ja piiratud heitgaasi kaudu:

Kui kolb siseneb padjakambrisse, on heitgaasi tee piiratud.
Sulgunud õhk surub kokku, tekitades suureneva vasturõhu.
See vasturõhk tekitab vasturõhu, mis aeglustab kolvi
Aeglustusprofiil sõltub padjakonstruktsioonist ja reguleerimisest.

Optimaalse pehmendusaja arvutamine

Optimaalne pehmendusaeg tasakaalustab löögi vältimise ja tsükli tõhususe:

Parameeter	Valem	Näide
Pehmendav kaugus	Põhineb silindrite konstruktsioonil	15 mm (tüüpiline 40 mm läbimõõdu puhul)
Nõutav aeglustus	a = v²/(2s)	V=0,5m/s, s=15mm: a = 8,33m/s².
Pehmendav aeg	t = √(2s/a)	t = √(2×0,015/8,33) = 0,06s
Rõhu kogunemine	P = P₀(V₀/V)^γ	Sõltub padjakambri geomeetriast

Pehmendusvõimet mõjutavad tegurid

Mitmed tegurid mõjutavad tegelikku pehmendustõhusust:

Pehmendustihendi konstruktsioon: Mõjutab õhulekkeid pehmenduse ajal.
Nõelklapi reguleerimine: Kontrollib heitgaasi piiramise määra
Liikuv mass: Raskemad koormused nõuavad pikemat pehmendusaega.
Lähenemiskiirus: Suuremad kiirused nõuavad pikemat pehmendusdistantsi
Töörõhk: Mõjutab maksimaalset kasutatavat vastujõudu

Pehmendustüübid ja nende rakendused

Erinevate rakenduste jaoks sobivad erinevad pehmendusmehhanismid:

Pehmendustüüp	Omadused	Parimad rakendused
Fikseeritud pehmendus	Lihtne, reguleerimata	Kerged koormused, järjepidev töö
Reguleeritav pehmendus	Reguleeritav nõelklappidega	Erinevad koormused, paindlikud rakendused
Isereguleeriv pehmendus	Kohaneb erinevate tingimustega	Muutuvad kiirused ja koormused
Välised amortisaatorid	Kõrge energia neeldumine	Rasked koormused, suured kiirused
Elektrooniline pehmendus	Täpselt kontrollitud aeglustamine	Servopneumaatilised süsteemid

Juhtumiuuring: Pehmenduste optimeerimine suure tsükliga rakendustes

Töötasin hiljuti koos Thomasega, kes on disainiinsener Saksamaal asuvas autoosade tootjas. Tema koosteliinil kasutati vardata silindreid, mis töötasid 45 tsükliga minutis, kuid neil esines sageli tihendite tõrkeid ja kinnitusklambrite kahjustusi.

Analüüs näitas, et pehmendusaeg oli liikuva massi jaoks liiga lühike, põhjustades löögijõudu peaaegu 3 % mõlemas löögi otsas. Pehmendushoogu suurendades 12 mm-lt 20 mm-le ja optimeerides nõelaventiili seadeid, pikendasime pehmendusaega 0,04 s-lt 0,07 s-le.

See näiliselt väike muudatus vähendas löögijõudu üle 60%, kõrvaldas täielikult klambrikahjustused ja pikendas tihendi kasutusiga 3 kuult üle aasta - ja seda kõike nõutava tsükli kestuse säilitamise juures.

Praktiline pehmenduse reguleerimise protseduur

Optimaalse pehmendusvõime saavutamiseks vardata silindrites:

Alustage täielikult avatud padjaklappidega (minimaalne piirang).
Sulgege järk-järgult pehmendusklappi, kuni saavutatakse sujuv aeglustumine.
Katse minimaalse ja maksimaalse eeldatava koormusega
Kontrollida pehmendusvõimet kogu kiirusvahemiku ulatuses.
Kuulake, kas löögiheli viitab ebapiisavale pehmendusele.
Mõõtke arvutuste kinnitamiseks tegelikku aeglustusaega.

Kokkuvõte

Kolbikinemaatika põhimõtete mõistmine - alates rõhunõuetest konstantse kiiruse saavutamiseks kuni kiirenduspiirangute ja pehmendusaja arvutamiseni - on tõhusate ja usaldusväärsete pneumaatikasüsteemide projekteerimiseks hädavajalik. Kui rakendate neid põhimõtteid oma vardata silindrirakendustes, saate optimeerida jõudlust, vähendada energiatarbimist ja pikendada märkimisväärselt komponentide kasutusiga.

Korduma kippuvad küsimused kolvikinemaatika kohta pneumaatilistes süsteemides

Millist rõhku on vaja konkreetse silindri kiiruse jaoks?

Vajalik surve sõltub koormusest, hõõrdumisest ja silindri pindalast. Arvutage see, kasutades P = (F + Fr)/A, kus F on väline koormusjõud, Fr on hõõrdetakistus ja A on kolvi pindala. Tüüpilise vardata silindri puhul, mis liigutab 10 kg raskust koormust horisontaalselt, on stabiilseks liikumiseks mõõdukal kiirusel vaja umbes 1,5-2 baari.

Kui kiiresti saab pneumosilinder kiirendada?

Pneumosilindri maksimaalne kiirendus arvutatakse, kasutades a = (P × A - F - Fr)/m. Tüüpilised vardata balloonid võivad saavutada kiirendust 10-25 m/s² sõltuvalt konstruktsioonist. See tähendab, et optimaalsetes tingimustes saavutatakse kiirus 0,5 m/s umbes 20-50 millisekundiga.

Millised tegurid piiravad vardata silindri maksimaalset kiirust?

Maksimaalne kiirus on piiratud klapi vooluvõimsuse, õhuvarustuse mahu, portide suuruse, pehmendusvõime ja tihendite konstruktsiooniga. Enamik standardseid vardata silindreid on kavandatud maksimaalseks kiiruseks 0,8-1,5 m/s, kuigi spetsialiseeritud kiiruskonstruktsioonid võivad ulatuda 2-3 m/s.

Kuidas arvutan oma rakenduse jaoks sobiva pehmenduse?

Arvutage nõuetekohane pehmendus, määrates liikuva koormuse kineetilise energia (KE = ½mv²) ja tagades, et pehmendussüsteem suudab selle energia absorbeerida. Pehmendusaeg tuleks arvutada, kasutades t = √(2s/a), kus s on padja kaugus ja a on soovitud aeglustuskiirus.

Mis juhtub, kui minu pneumosilinder kiirendab liiga kiiresti?

Liigne kiirendus võib põhjustada mehaanilist koormust paigaldusosadele, tihendite enneaegset kulumist, suurenenud vibratsiooni ja müra, võimalikku koormuse nihkumist või kahjustusi ning süsteemi täpsuse vähenemist. Samuti võib see põhjustada hüppelist liikumist, mis mõjutab toote kvaliteeti täppisrakendustes.

Kuidas mõjutab koormuse orientatsioon liikumiseks vajalikku survet?

Koormuse orientatsioon mõjutab oluliselt rõhu nõudeid. Vastupidiselt raskusjõule liikuvad vertikaalsed koormused vajavad gravitatsioonijõu ületamiseks lisarõhku (P = F/A + Fg/A + Fr/A). Horisontaalsed koormused peavad ületama ainult hõõrdumise ja inertsuse. Kaldu koormused jäävad nende äärmuslike väärtuste vahele, mis põhineb nurga siinusel.

Selgitab põhjalikult kineetikat, mehaanika haru, mis kirjeldab objektide liikumist ilma liikumist põhjustavaid jõude arvestamata.
elektrooniline sisendsignaal, mis võimaldab täiustatud pneumaatilist juhtimist. ↩
Üksikasjad Newtoni teisest seadusest (F=ma), mis on füüsika aluspõhimõte, mis seob objektile mõjuvat jõudu selle massi ja kiirendusega ning mis on aluseks kõikidele dünaamilistele arvutustele. ↩
Kirjeldab servopneumaatikat, täiustatud juhtimistehnoloogiat, mis ühendab pneumaatika võimsuse ja suletud ahela elektroonilise juhtimise täpsuse, et saavutada väga täpne positsioneerimine ja liikumisprofiilid. ↩

Tere, ma olen Chuck, vanemekspert, kellel on 15-aastane kogemus pneumaatikatööstuses. Bepto Pneumaticus keskendun kvaliteetsete ja kohandatud pneumaatiliste lahenduste pakkumisele meie klientidele. Minu teadmised hõlmavad tööstusautomaatikat, pneumaatikasüsteemide projekteerimist ja integreerimist, samuti võtmekomponentide rakendamist ja optimeerimist. Kui teil on küsimusi või soovite arutada oma projekti vajadusi, võtke minuga ühendust aadressil chuck@bepto.com.