Kas teil on probleeme aeglase silindri kiiruse, ebajärjekindla liikumise või ebapiisava jõuga oma pneumaatikasüsteemides? Need levinud probleemid tulenevad sageli valesti mõistetud süüdlasest: voolutakistus. Paljud insenerid mõõdavad oma pneumaatilised komponendid üksnes rõhu ja jõunõuete alusel, jättes tähelepanuta voolutakistuse kriitilise mõju tegelikule toimivusele.
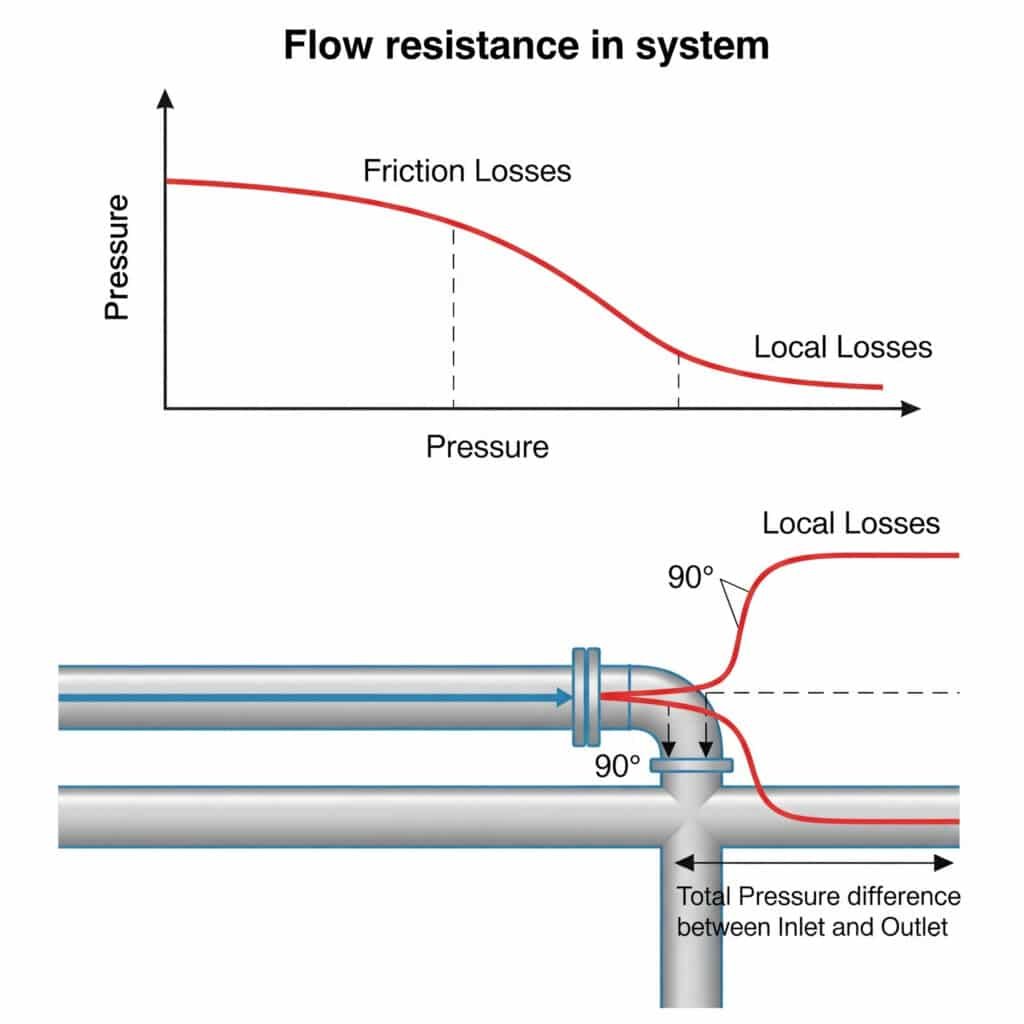
Pneumosüsteemide voolutakistus tekitab rõhulangusi, mis vähendavad kasutatavat jõudu, piiravad maksimaalset kiirust ja põhjustavad ebajärjekindlaid liikumisi. See takistus tuleneb nii hõõrdumisest piki sirgeid torusid (hõõrdekadu) kui ka katkestustest liitmike, paindude ja ventiilide juures (kohalikud kaod). Koos võivad need takistused vähendada süsteemi tegelikku jõudlust 20-50% võrra võrreldes teoreetiliste arvutustega.
Enam kui 15 aastat Beptos pneumaatiliste süsteemidega töötades olen näinud lugematul hulgal juhtumeid, kus voolutakistuse mõistmine ja lahendamine on muutnud alatöötavad süsteemid usaldusväärseteks ja tõhusateks operatsioonideks. Lubage mul jagada seda, mida olen õppinud nende varjatud jõudluse hävitajate arvutamise ja minimeerimise kohta.
Sisukord
- Kuidas tegelikult arvutada hõõrdekadusid pneumaatilistes liinides?
- Miks on ekvivalentse pikkuse meetod süsteemi täpseks projekteerimiseks kriitiline?
- Mis juhtub, kui õhk voolab läbi vähendatud läbimõõduga lõigete?
- Kokkuvõte
- Korduma kippuvad küsimused voolutakistuse kohta pneumaatilistes süsteemides
Kuidas tegelikult arvutada hõõrdekadusid pneumaatilistes liinides?
Hõõrdekadu sirgetes torudes on voolutakistuse arvutuste aluseks, kuid paljud insenerid tuginevad liiga lihtsustatud rusikareeglitele, mis viivad süsteemide alamõõdistamiseni.
Pneumoliinide hõõrdekadusid arvutatakse kasutades Darcy-Weisbachi võrrand1: ΔP = λ(L/D)(ρv²/2), kus λ on hõõrdetegur, L on toru pikkus, D on toru läbimõõt, ρ on õhu tihedus ja v on voolukiirus. Pneumaatiliste süsteemide puhul sõltub hõõrdetegur λ järgmisest Reynoldsi arv2 ja suhteline karedus ning see määratakse tavaliselt otsingutabeli või Moody diagramm3.
Hõõrdekadude mõistmisel on praktiline mõju süsteemi projekteerimisele ja tõrkeotsingule. Lubage mul jagada see käepäraseks arusaamiseks.
Hõõrdeteguri tabelite tõhus kasutamine
Hõõrdetegur (λ) on peamine parameeter rõhulanguse arvutamisel, kuid selle väärtuse määramiseks tuleb arvesse võtta voolutingimusi:
| Voolurežiim | Reynoldsi arv (Re) | Hõõrdeteguri määramine |
|---|---|---|
| Laminaarne voolu | Re < 2000 | λ = 64/Re |
| Üleminekuvoog | 2000 < Re < 4000 | Ebausaldusväärne - vältige projekteerimist selles vahemikus. |
| Turbulentne voolu | Re > 4000 | Kasutage suhtelisel karedusel (ε/D) põhinevaid tabeleid. |
Praktiline hõõrdeteguri tabel
Pneumaatiliste süsteemide turbulentse voolu puhul kasutage seda lihtsustatud tabelit:
| Toru materjal | Suhteline karedus (ε/D) | Hõõrdetegur (λ) tavaliste Reynoldsi arvude juures |
|---|---|---|
| Re = 10,000 | ||
| Siledad torud (PVC, polüuretaan) | 0.0001 – 0.0005 | 0.031 |
| Alumiiniumtorud | 0.001 – 0.002 | 0.035 |
| Tsingitud teras | 0.003 – 0.005 | 0.042 |
| Roostetanud teras | 0.01 – 0.05 | 0.054 |
Rõhulanguse arvutamine reaalsetes pneumaatilistes süsteemides
Käime läbi ühe praktilise näite:
| Parameeter | Väärtus/arvutus | Näide |
|---|---|---|
| Toru läbimõõt (D) | Sisemine läbimõõt | 8mm (0,008m) |
| Toru pikkus (L) | Sirge kogupikkus | 5m |
| Vooluhulk (Q) | Alates süsteeminõuetest | 20 standardset liitrit sekundis |
| Õhu tihedus (ρ) | Töörõhu juures | 7,2 kg/m³ 6 baari juures |
| Voolukiirus (v) | v = Q/(π×D²/4) | v = 0,02m³/s/(π×0,008²/4) = 398 m/s |
| Reynoldsi arv (Re) | Re = ρvD/μ | Re = 7,2×398×0,008/1,8×10-⁵ = 1,273,600 |
| Suhteline karedus | Polüuretaantorude jaoks | 0.0003 |
| Hõõrdetegur (λ) | Otsingutabeli järgi | 0.017 |
| Rõhu langus (ΔP) | ΔP = λ(L/D)(ρv²/2) | ΔP = 0,017×(5/0,008)×(7,2×398²/2) = 6,07 bar |
Reaalse maailma rakendus: Silindri kiiruse probleemide lahendamine
Eelmisel aastal töötasin koos Sarah'ga, kes oli tootmisinsener ühes Wisconsini pakendiseadmete ettevõttes. Tema vardata balloonisüsteem töötas ainult 60% oodatavast kiirusest, kuigi tal oli õige suurusega balloon ja piisav varustusrõhk.
Pärast tema süsteemi analüüsimist avastasin, et ta kasutas 6 mm torusid suure vooluhulgaga rakenduse jaoks. Hõõrdekadu põhjustas 2,1 baarise rõhu languse, mis vähendas oluliselt olemasolevat jõudu ja kiirust. Uuendades süsteemi 10 mm torudele, vähendasime rõhulangust 0,4 baarini ja tema süsteem saavutas kohe nõutava jõudluse ilma muude muudatusteta.
Reaalsete süsteemide hõõrdekadusid mõjutavad tegurid
Tegelikke hõõrdekadusid mõjutavad mitmed tegurid:
- Õhutemperatuur: Kõrgemad temperatuurid suurendavad viskoossust ja hõõrdumist
- Saastumine: Mustus ja õli võivad suurendada efektiivset karedust
- Torude painutamine: Painutatud torude mikrodeformatsioon suurendab vastupanu
- Vanuse halvenemine: Korrosioon ja ladestumine suurendavad aja jooksul karedust
- Töörõhk: Suurem rõhk suurendab tihedust ja kadusid
Miks on ekvivalentse pikkuse meetod süsteemi täpseks projekteerimiseks kriitiline?
Kohalikud kaod liitmike, ventiilide ja kurvide juures on sageli suuremad kui hõõrdekadu sirgetes torudes, kuid paljud insenerid kas ignoreerivad neid või kasutavad jämedaid hindamismeetodeid, mis toovad kaasa töövõime probleeme.
Ekvivalentse pikkuse meetod teisendab liitmike ja ventiilide kohalikke kadusid samaväärseks sirge toru pikkuseks, mis põhjustaks sama rõhulanguse. Selle arvutamiseks kasutatakse Le = K(D/λ), kus Le on ekvivalentne pikkus, K on kohalik kadude koefitsient4, D on toru läbimõõt ja λ on hõõrdetegur. See meetod lihtsustab arvutusi ja annab täpsemaid prognoose süsteemi jõudluse kohta.
Uurime, kuidas seda meetodit tõhusalt rakendada pneumaatiliste süsteemide projekteerimisel.
Tavaliste pneumaatiliste komponentide ekvivalentse pikkuse tabelid
Siin on praktiline tabel tavaliste pneumaatiliste komponentide kohta:
| Komponent | K-väärtus | Ekvivalentne pikkus (Le/D) |
|---|---|---|
| 90° küünarnukk (terav) | 0.9 | 30 |
| 90° küünarnukk (standardne raadius) | 0.3 | 10 |
| 45° küünarnukk | 0.2 | 7 |
| T-ühendus (läbivool) | 0.3 | 10 |
| T-liitumine (hargnevus) | 1.0 | 33 |
| Kuulklapp (täielikult avatud) | 0.1 | 3 |
| Väravaventiil (täielikult avatud) | 0.2 | 7 |
| Kiirühendusliitmik | 0.4-0.8 | 13-27 |
| Tagasilöögiklapp | 1.5-2.5 | 50-83 |
| Standardne voolu reguleerimisventiil | 1.0-3.0 | 33-100 |
Ekvivalentse pikkuse meetodi rakendamine
Selle meetodi tõhusaks kasutamiseks:
- Identifitseerige kõik pneumaatilise vooluahela komponendid
- Leida iga komponendi K-väärtus või ekvivalentne pikkuse suhe (Le/D).
- Arvutage ekvivalentne pikkus, korrutades selle toru läbimõõduga.
- Lisage kõik samaväärsed pikkused tegelikule sirge toru pikkusele.
- Kasutage kogu efektiivset pikkust oma hõõrdekadude arvutustes.
Näiteks süsteem, mis koosneb 5 m 8 mm pikkusest sirgest torust ning neljast 90° nurgakumerest, ühest T-liitmikust ja kahest kiirliitmikust:
| Komponent | Kogus | Le/D | Ekvivalentne pikkus |
|---|---|---|---|
| 90° põlved | 4 | 10 | 4 × 10 × 0,008m = 0,32m |
| T-ühendus | 1 | 10 | 1 × 10 × 0,008m = 0,08m |
| Kiirühendused | 2 | 20 | 2 × 20 × 0,008m = 0,32m |
| Ekvivalentne kogupikkus | 0.72m | ||
| Tegelik sirge pikkus | 5.00m | ||
| Efektiivne kogupikkus | 5.72m |
See tähendab, et teie 5m süsteem käitub tegelikult nagu 5,72m süsteem kohalike kadude tõttu - 14,4% efektiivse pikkuse suurenemine.
Juhtumiuuring: Klappide paigutuse optimeerimine montaažisüsteemides
Hiljuti aitasin Migueli, kes on automaatika insener ühes Arizona elektroonikatehases. Tema pick-and-place-süsteemis esinesid ebakindlad liikumis- ja tsükliaegade kõikumised, hoolimata kvaliteetsete komponentide kasutamisest.
Analüüs näitas, et tema klapikollektor asus balloonidest 3 m kaugusel ja vooluahelas oli arvukalt liitmikke. Ekvivalentse pikkuse arvutus näitas, et tema tegelik 3m kaugus oli kohalike kadude tõttu 7,2m - rohkem kui kaks korda pikem kui sirge toru kaugus!
Viies klapikollektori silindritele lähemale ja kõrvaldades mitu liitmikku, vähendasime tegelikku pikkust 7,2 meetrilt 2,1 meetrile. See vähendas rõhulangust 70% võrra, mille tulemuseks oli ühtlane liikumine ja 15% võrra väiksem tsükli kestus.
Praktilised näpunäited kohalike kahjude minimeerimiseks
Pneumaatiliste süsteemide kohalike kadude vähendamiseks:
- Kasutage pühitud või ümardatud küünarnukke teravate kurvide asemel (vähendab K-väärtust 67% võrra)
- Minimeerida liitmike arvu kavandades otsesemat marsruutimist
- Valige madala kitsendusega komponendid nagu täisläbimõõdulised kuulventiilid, kui see on asjakohane
- Sobiva suurusega liitmikud - alamõõdulised liitmikud põhjustavad ebaproportsionaalseid kahjusid
- Paigutage ventiilid ajamite lähedale vähendada torude tegelikku pikkust
Mis juhtub, kui õhk voolab läbi vähendatud läbimõõduga lõigete?
Pneumaatiliste vooluahelate vähendatud läbimõõduga osad - näiteks osaliselt suletud ventiilid, alamõõdulised liitmikud või läbimõõdu üleminekud - tekitavad märkimisväärseid voolupiiranguid, mis võivad süsteemi jõudlust tõsiselt mõjutada.
Kui õhk voolab läbi vähendatud läbimõõduga lõigete, rõhu langus5 toimuvad vastavalt valemile ΔP = ρ(v₂² - v₁²)/2, kus v₁ on kiirus enne piirangut ja v₂ on kiirus piirangus. Seda saab kompenseerida, kasutades puurimissuhte kompensatsioonitegurit C = (1 - (d/D)⁴), kus d on vähendatud läbimõõt ja D on algläbimõõt. See tegur aitab prognoosida süsteemi tegelikku jõudlust ja vältida komponentide alamõõtmist.
Uurime vähendatud läbimõõduga lõigete praktilisi tagajärgi ja seda, kuidas neid süsteemi projekteerimisel arvesse võtta.
Rõhupisarate arvutamine läbimõõdu üleminekutel
Kui õhk voolab suuremast läbimõõdust väiksemasse, saab rõhulangust arvutada, kasutades:
| Parameeter | Valem | Näide |
|---|---|---|
| Algne läbimõõt (D) | Spetsifikatsioonidest | 10mm |
| Vähendatud läbimõõt (d) | Spetsifikatsioonidest | 6mm |
| Läbimõõdu suhe (d/D) | Lihtne jagamine | 0.6 |
| Vooluhulk (Q) | Alates süsteeminõuetest | 15 standardset liitrit sekundis |
| Kiirus algses torus (v₁) | v₁ = Q/(π×D²/4) | 191 m/s |
| Kiirus vähendatud sektsioonis (v₂) | v₂ = Q/(π×d²/4) | 531 m/s |
| Rõhu langus (ΔP) | ΔP = ρ(v₂² - v₁²)/2 | 0,88 bar |
| Kompensatsioonitegur (C) | C = (1 - (d/D)⁴) | 0.87 |
Üldised puuraugu vähendamise stsenaariumid ja nende mõju
Siin on näha, kuidas erinevad puuraukude vähendamised mõjutavad vooluvõimsust:
| Puuraukude vähendamine | Vooluvõimsuse vähendamine | Rõhu languse suurenemine |
|---|---|---|
| 10mm kuni 8mm | 36% | 2.4× |
| 10mm kuni 6mm | 64% | 7.7× |
| 10mm kuni 4mm | 84% | 39× |
| 8mm kuni 6mm | 44% | 3.2× |
| 8mm kuni 4mm | 75% | 16× |
| 6mm kuni 4mm | 56% | 5.1× |
Need arvud näitavad, miks näiliselt väikesed läbimõõdu vähendamised võivad avaldada dramaatilist mõju süsteemi jõudlusele.
Mitme piirangu kumulatiivne mõju
Reaalsetes pneumaatilistes vooluahelates esineb mitu piirangut järjestikku. Nende mõju on kumulatiivne ja seda saab arvutada kasutades:
- Iga piirangu teisendamine samaväärseks C-teguriks.
- Arvutage kogu C-tegur: Ctotal = 1 - (1-C₁)(1-C₂)(1-C₃)...
- Kasutage seda kogutegurit, et määrata süsteemi üldine jõudluse vähenemine.
Juhtumiuuring: Klapi ja ajami sobimatusprobleemide lahendamine
Eelmisel kuul töötasin koos Thomasega, kes on hooldusülem Põhja-Carolinas asuvas mööblitootmisettevõttes. Tema uus vardata silindrisüsteem töötas vähem kui poole oodatud kiirusega, hoolimata sellest, et kasutas tootja soovitatud klapi suurust.
Uurimine näitas, et tema vooluahelas on mitu puuri vähendamist:
- 10mm toitevoolik 8mm klapiportidele (C₁ = 0,36)
- 8mm klapipordi ja 6mm liitmike vahel (C₂ = 0,44)
- 6mm liitmikud 8mm silindriportidele koos sisemiste piirangutega (C₃ = 0,32)
Kogu kompensatsioonitegur oli Ctotal = 1 - (1-0,36)(1-0,44)(1-0,32) = 0,75, mis tähendab, et tema süsteem kaotas 75% oma teoreetilisest vooluvõimsusest!
Parandades kogu süsteemi õigesti dimensioneeritud komponentidega, kõrvaldasime need piirangud ja saavutasime nõutava jõudluse ilma ballooni või toiterõhku muutmata.
Praktilised strateegiad puuraugude vähendamise kahjude minimeerimiseks
Puuraukude vähendamisest tulenevate kahjude vähendamiseks:
- Komponentide suurus järjekindlalt kogu pneumaatilise vooluahela ulatuses
- Kasutage suurimat praktilist torude suurust suure vooluhulgaga rakenduste jaoks
- Pöörake tähelepanu sisekomponentide piirangutele, mitte ainult ühenduse suurused
- Kaaluda paralleelseid vooluteid suure vooluhulgaga nõuete puhul
- Kõrvaldage ebavajalikud adapterid ja üleminekud. võimaluse korral
"Nõrgima lüli" põhimõte pneumaatilistes süsteemides
Pidage meeles, et teie pneumosüsteemi jõudlust piirab selle kõige piiravam komponent. Ükski alamõõduline element võib tühistada õigesti mõõdetud komponentide eelised mujal süsteemis.
Näiteks süsteem, milles on 10 mm torud, 10 mm ventiilid, kuid 6 mm liitmikud silindri juures, töötab sisuliselt sama hästi kui süsteem, milles on kõikjal 6 mm komponendid - ainult et see on kallim.
Kokkuvõte
Voolutakistuse mõistmine ja nõuetekohane arvutamine - hõõrdetegurite tabelite, ekvivalentse pikkuse meetodite ja vähendatud läbimõõdu kompenseerimise abil - on oluline selliste pneumosüsteemide projekteerimiseks, mis toimivad tegelikes tingimustes ootuspäraselt. Neid arvutusmeetodeid ja projekteerimispõhimõtteid rakendades saate optimeerida oma vardata silindrirakendusi ja muid pneumaatilisi süsteeme maksimaalse jõudluse ja töökindluse saavutamiseks.
Korduma kippuvad küsimused voolutakistuse kohta pneumaatilistes süsteemides
Kui suur rõhulangus on pneumaatilises süsteemis vastuvõetav?
Aktsepteeritav rõhulangus sõltub teie rakenduse nõuetest, kuid üldjuhendina piirake tõhusaks tööks kogu rõhulangust 10-15% toiterõhust. See tähendab, et 6 baari süsteemi puhul peab kogu rõhulangus jääma alla 0,6-0,9 baari. Kriitilised rakendused võivad vajada veelgi väiksemat rõhulangust 5-8%, et säilitada püsiv jõudlus.
Milline on toru läbimõõdu ja rõhulanguse suhe?
Pneumaatiliste süsteemide turbulentse voolu puhul on rõhulangus pöördvõrdeline läbimõõdu viienda võimsusega (D⁵). See tähendab, et toru läbimõõdu kahekordistamine vähendab rõhulangust ligikaudu 32 korda. Näiteks võib 6 mm torude suurendamine 12 mm torudele vähendada rõhulangust 1,5 baarilt vaid 0,047 baarini samade voolutingimuste korral.
Kuidas määrata oma pneumaatilise rakenduse jaoks õige torusuurus?
Valige toru suurus vastavalt voolukiiruse nõuetele ja vastuvõetavale rõhulangusele. Arvutage Reynoldsi arv ja hõõrdetegur, seejärel kasutage Darcy-Weisbachi võrrandit, et määrata rõhulangus erinevate läbimõõtude puhul. Valige väikseim läbimõõt, mis hoiab rõhulanguse vastuvõetavates piirides (tavaliselt <10% toiterõhust), võttes samas arvesse ruumipiiranguid ja kulusid.
Kumb tekitab rohkem piiranguid: 90° küünarnukk või 5 meetrit sirget toru?
Terav 90° küünarnukk tekitab tavaliselt vastupanu, mis on võrdne 30 toru läbimõõduga sirge toruga. 8 mm torude puhul võrdub üks terav küünarnukk ligikaudu 240 mm (30 × 8 mm) sirge toru läbimõõduga. See tähendab, et 5 meetrit sirget toru tekitab umbes 21 korda rohkem piiranguid kui üks küünarnukk. Süsteemid sisaldavad siiski sageli mitu põlve ja liitmikku, mille kumulatiivne mõju võib ületada sirge pikkusega kadusid.
Kuidas mõjutavad kiirliitmikud süsteemi jõudlust?
Standardsed kiirühendused põhjustavad tavaliselt 15-25 toru läbimõõduga sirgete torude kohalikke kadusid. Veelgi olulisem on see, et paljudel kiirühendustel on sisemised piirangud, mis on väiksemad kui nende nimimõõdud. "10 mm" kiirühendusel võib olla ainult 7-8 mm sisemine kitsendus, mis vähendab läbimõõdu 50-70% võrra.
Milline on osaliselt suletud voolu reguleerimisventiilide mõju süsteemi jõudlusele?
Voolu reguleerimisventiil, mis on suletud 50% ulatuses oma täisläbimõõdu pindalast, ei vähenda voolu ainult 50% võrra - see vähendab voolu ligikaudu 75% võrra, mis tuleneb läbimõõdu ja voolu võimsuse mittelineaarsest suhtest. Rõhulangus suureneb vastavalt kiiruse muutuse ruudule, seega efektiivse läbimõõdu vähendamine poole võrra suurendab rõhulangust ligikaudu 16 korda samade voolutingimuste korral.
-
Annab üksikasjaliku ülevaate Darcy-Weisbachi võrrandist, mis on vedelikudünaamikas põhiline ja laialdaselt kasutatav valem, et arvutada hõõrdumisest tingitud survekadu torus. ↩
-
Pakub Reynoldsi arvu selget määratlust, mis on kriitiline mõõtmeta suurus, mida kasutatakse voolumustrite (laminaarse või turbulentse) prognoosimiseks erinevates vedeliku voolu olukordades. ↩
-
Tutvustab Moody diagrammi, põhjalikku graafikut, mis kujutab Darcy hõõrdetegurit Reynoldsi arvu ja suhtelise kareduse suhtes, mis on inseneridele standardne vahend torude rõhulanguse määramiseks. ↩
-
Selgitab K-väärtuse ehk kohaliku kadude koefitsiendi mõistet, mis on mõõtmeta arv, mida kasutatakse toruliitmiku või -ventiili rõhukao iseloomustamiseks samaväärse pikkuse meetodi osana. ↩
-
Üksikasjalikult kirjeldatakse füüsikat, mis on seotud rõhulangusega, mis tekib, kui vedelik läbib kitsendust (ava), tuginedes pidevuse võrrandi ja Bernoulli printsiibi põhimõtetele. ↩



