Insenerid arvutavad pneumosilindrisüsteemide projekteerimisel sageli vardapindu valesti, mis viib ebaõigete jõuarvutusteni ja süsteemi talitlusvigade tekkimiseni.
Varda pindala on ringikujulise ristlõike pindala, mis arvutatakse järgmiselt: A = πr² või A = π(d/2)², kus "r" on varda raadius ja "d" on varda läbimõõt, mis on kriitiline jõu ja rõhu arvutuste jaoks.
Eile aitasin ma Carlosit, Mehhiko konstruktorit, kelle pneumosüsteem ebaõnnestus, sest ta unustas kahetoimelise silindri jõuarvutustes kolvi pindalast maha arvata varda pindala.
Sisukord
- Mis on pneumaatiliste silindrisüsteemide vardapind?
- Kuidas arvutada varda ristlõike pindala?
- Miks on varda pindala jõudude arvutamisel oluline?
- Kuidas mõjutab varda pindala silindri jõudlust?
Mis on pneumaatiliste silindrisüsteemide vardapind?
Varda pindala on kolbvarraste ümmargune ristlõike pindala, mis on oluline kolvi efektiivsete pindalade ja jõu väljundite arvutamiseks kahetoimelistes pneumosilindrites.
Varda pindala on kolbvarraste ristlõike poolt hõivatud ringikujuline pindala, mis on mõõdetud risti varda teljega ja mida kasutatakse jõuarvutuste jaoks efektiivsete netopindalade määramiseks.
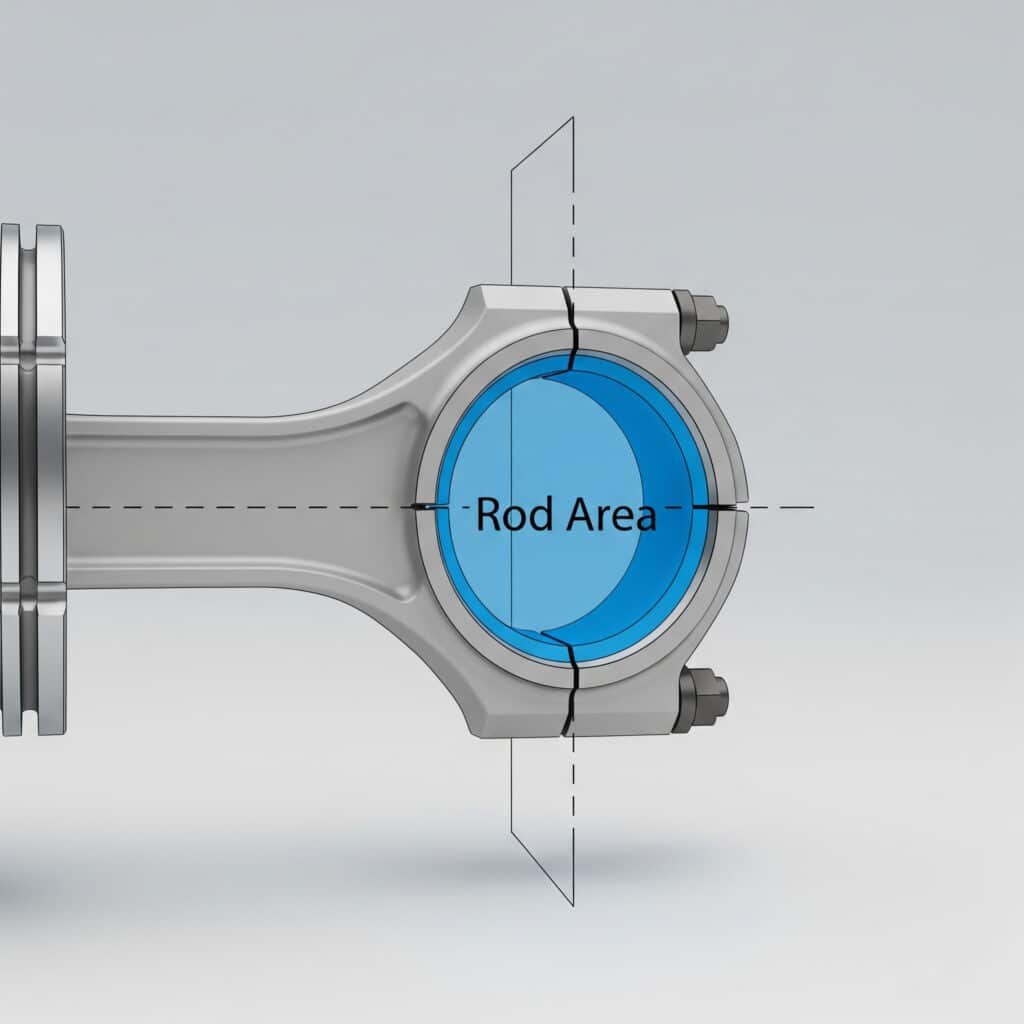
Varda piirkonna määratlus
Geomeetrilised omadused
- Ringikujuline ristlõige: Standardne varraste geomeetria
- Risti mõõtmine: 90° varda keskjoone suhtes
- Pidev pindala: Ühetaoline piki varraste pikkust
- Tahke ala: Täielik materjali läbilõige
Peamised mõõtmised
- Varda läbimõõt: Esmane mõõde pindala arvutamiseks
- Varda raadius: Pool läbimõõdu mõõtmisest
- Ristlõike pindala: Ringikujulise pindala valemi taotlus
- Efektiivne pindala: Mõju silindri jõudlusele
Varda ja kolvi pindala suhe
| Komponent | Pindala valem | Eesmärk | Taotlus |
|---|---|---|---|
| Kolvi | A = π(D/2)² | Täispuurimisala | Laiendada jõuarvutust |
| Rod | A = π(d/2)² | Varda ristlõige | Tagasitõmbamisjõu arvutamine |
| Netopindala | A_kolb - A_varras | Efektiivne sisselõikepindala | Kahepoolse toimega silindrid |
| Rõngakujuline ala1 | π(D² - d²)/4 | Rõngakujuline ala | Varda poolne rõhk |
Standardsed varraste suurused
Tavalised varraste läbimõõdud
- 8mm varras: Pindala = 50,3 mm²
- 12mm varras: Pindala = 113,1 mm²
- 16mm varras: Pindala = 201,1 mm²
- 20mm varras: Pindala = 314,2 mm²
- 25mm varras: Pindala = 490,9 mm²
- 32mm varras: Pindala = 804,2 mm²
Varda ja puuraugu suhe
- Standardne suhe: Varda läbimõõt = 0,5 × ava läbimõõt
- Raskeveokite: Varda läbimõõt = 0,6 × ava läbimõõt
- Kerge töö: Varda läbimõõt = 0,4 × ava läbimõõt
- Kohandatud rakendused: Varieerub vastavalt nõuetele
Varda piirkonna rakendused
Jõu arvutused
Ma kasutan varda ala:
- Laiendada jõudu: Täielik kolvi pindala × rõhk
- Tagasitõmbamise jõud: (kolvi pindala - varda pindala) × rõhk
- Jõu erinevus: Erinevus pikendamise/tagasivõtmise vahel
- Koormuse analüüs: Silindri sobitamine rakendusega
Süsteemi projekteerimine
Varda piirkond mõjutab:
- Silindri valik: Õige mõõtmine rakenduste jaoks
- Kiiruse arvutused: Voolunõuded igale suunale
- Survenõuded: Süsteemi rõhu spetsifikatsioonid
- Jõudluse optimeerimine: Tasakaalustatud töökorraldus
Varraste pindala eri silindritüüpides
Ühetoimelised balloonid
- Mõju varraste piirkonnale puudub: Vedru tagastamise operatsioon
- Ainult jõu laiendamine: Täielik kolvi pindala efektiivne
- Lihtsustatud arvutused: Tagasitõmbevõimega arvestamine puudub
- Kulude optimeerimine: Vähendatud keerukus
Kahepoolse toimega silindrid
- Kriitiline varraste piirkond: Mõjutab sissetõmbamisjõudu
- Asümmeetriline toiming: Erinevad jõud igas suunas
- Keerulised arvutused: Peab arvestama mõlemaid valdkondi
- Tulemuslikkuse tasakaalustamine: Nõutavad projekteerimisega seotud kaalutlused
Vardata silindrid
- Puudub varraste ala: Disainist kõrvaldatud
- Sümmeetriline toiming: Võrdsed jõud mõlemas suunas
- Lihtsustatud arvutused: Ühe piirkonna kaalutlus
- Ruumilised eelised: Puuduvad nõuded varraste pikendamiseks
Kuidas arvutada varda ristlõike pindala?
Pneumosüsteemi täpseks projekteerimiseks kasutatakse varda ristlõike pindala arvutamisel standardset ringikujulise pindala valemit koos varda läbimõõdu või raadiuse mõõtmistega.
Arvutage varda pindala, kasutades A = πr² (raadiusega) või A = π(d/2)² (läbimõõduga), kus π = 3,14159, tagades kogu arvutuses ühtsed mõõtühikud.
Põhiline pindala valem
Kasutades Rod Radius
A = πr²
- A: Varda ristlõike pindala
- π: 3.14159 (matemaatiline konstant)
- r: Varda raadius (läbimõõt ÷ 2)
- Üksused: Pindala raadiuse ühikutes ruutu
Kasutades varda läbimõõtu
A = π(d/2)² või A = πd²/4
- A: Varda ristlõike pindala
- π: 3.14159
- d: Varda läbimõõt
- Üksused: Pindala läbimõõduühikutes ruutühikutes
Samm-sammult arvutamine
Mõõtmisprotsess
- Mõõtke varda läbimõõt: Kasutage täpsuse tagamiseks kalibreid
- Kontrollida mõõtmist: Võtke mitu lugemist
- Arvuta raadius: r = läbimõõt ÷ 2 (kui kasutatakse raadiuse valemit)
- Rakenda valemit: A = πr² või A = π(d/2)²
- Kontrollida üksusi: Tagada järjepidev ühikusüsteem
Arvutuse näide
20 mm läbimõõduga varda jaoks:
- Meetod 1: A = π(10)² = π × 100 = 314,16 mm².
- Meetod 2: A = π(20)²/4 = π × 400/4 = 314,16 mm².
- Kontrollimine: Mõlemad meetodid annavad identsed tulemused
Varda pindala arvutustabel
| Varda läbimõõt | Varda raadius | Pindala arvutamine | Rodi ala |
|---|---|---|---|
| 8mm | 4mm | π × 4² | 50,3 mm² |
| 12mm | 6mm | π × 6² | 113,1 mm² |
| 16mm | 8mm | π × 8² | 201,1 mm² |
| 20mm | 10mm | π × 10² | 314,2 mm² |
| 25mm | 12.5mm | π × 12.5² | 490,9 mm² |
| 32mm | 16mm | π × 16² | 804,2 mm² |
Mõõtmisvahendid
Digitaalsed kaliibrid
- Täpsus: ±0,02 mm täpsus
- Range: 0-150mm tüüpiline
- Omadused: Digitaalne ekraan, ühikute teisendamine
- Parim tava: Mitu mõõtepunkti
Mikromeeter
- Täpsus: ±0,001mm täpsus
- Range: Saadaval on erinevad suurused
- Omadused: Ratšistopp, digitaalsed valikud
- Rakendused: Suure täpsusega nõuded
Tavalised arvutusvead
Mõõtmisvead
- Läbimõõt vs raadius: Valemis vale mõõtme kasutamine
- Üksuse ebajärjekindlus: Millimeetrite ja tollide segamine
- Täpsusvead: Ebapiisavad kümnendkohad
- Tööriista kalibreerimine: Kalibreerimata mõõtevahendid
Valemi vead
- Vale valem: Pindala asemel ümbermõõdu kasutamine
- Puuduv π: Unustamine matemaatiline konstant
- Vead ruutude võrdlemisel: Eksponendi ebaõige kasutamine
- Ühiku teisendamine: Ebakorrektsed ühiku teisendused
Kontrollimise meetodid
Ristkontrolli tehnikad
- Mitmekordsed arvutused: Erinevad valemimeetodid
- Mõõtmise kontrollimine: Läbimõõdu mõõtmiste kordamine
- Viitetabelid: Võrrelda standardväärtustega
- CAD tarkvara: 3D mudeli pindala arvutused
Mõistlikkuse kontroll
- Suuruse korrelatsioon: Suurem läbimõõt = suurem pindala
- Standardsed võrdlused: Vastavad tüüpilised varraste suurused
- Rakenduse sobivus: Sobib silindri suurusele
- Tootmisstandardid: Tavalised olemasolevad suurused
Täiustatud arvutused
Õõnsad vardad
A = π(D² - d²)/4
- D: Välisläbimõõt
- d: Sisemine läbimõõt
- Taotlus: Kaalu vähendamine, sisemine marsruutimine
- Arvutus: Sisemine pindala lahutatakse välimisest pindalast
Mitte-ringikujulised vardad
- Nelinurksed vardad: A = pool²
- Ristkülikukujulised vardad: A = pikkus × laius
- Erilised vormid: Kasutage asjakohaseid geomeetrilisi valemeid
- Rakendused: Vältida rotatsiooni, erinõuded
Kui ma töötasin koos Jenniferiga, Kanada pneumaatikasüsteemi projekteerijaga, arvutas ta algselt varda pindala valesti, kasutades πr² valemis raadiuse asemel läbimõõtu, mille tulemuseks oli 4× ülehindamine ja täiesti vale jõuarvutus tema kahetoimelise silindri rakenduse jaoks.
Miks on varda pindala jõudude arvutamisel oluline?
Varraste pindala mõjutab otseselt kolvi efektiivset pindala kahetoimeliste silindrite varraste poolel, tekitades jõuerinevusi välja- ja sissetõmbamistoimingute vahel.
Varraste pindala vähendab kolvi efektiivset pindala sisselõikamisel, tekitades väiksema sisselõikamisjõu võrreldes väljapoole suunatud jõuga kahetoimelistel silindritel, mis nõuab kompensatsiooni süsteemi projekteerimisel.
Jõu arvutamise alused
Põhiline jõu valem
- Laiendada jõudu: F = P × A_kolb
- Tagasitõmbamise jõud: F = P × (A_kolb - A_varras)
- Jõuvahe: Välja tõmbamisjõud > sissetõmbamisjõud
- Kujunduse mõju: Peab arvestama mõlemat suunda
Tõhusad piirkonnad
- Täielik kolbipindala: Saadaval laiendamise ajal
- Kolvi netopindala: Kolvi pindala miinus varda pindala tagasitõmbamisel
- Rõngakujuline ala: Rõngakujuline ala varraste poolel
- Pindala suhe: Määratleb jõu diferentseerimise
Jõu arvutamise näited
63mm puur, 20mm varras silinder
- Kolvi pindala: π(31,5)² = 3,117 mm².
- Varraste piirkond: π(10)² = 314 mm²
- Netopindala: 3,117 - 314 = 2,803 mm².
- 6 baari rõhu juures:
– Laiendada jõudu: 6 × 3,117 = 18,702 N
– Tagasitõmbamise jõud: 6 × 2,803 = 16,818 N
– Jõuvahe: 1,884 N (10% vähendamine)
Jõu võrdlustabel
| Silindri suurus | Kolvi pindala | Rodi ala | Netopindala | Jõu suhe |
|---|---|---|---|---|
| 32mm/12mm | 804 mm² | 113 mm² | 691 mm² | 86% |
| 50mm/16mm | 1,963 mm² | 201 mm² | 1,762 mm² | 90% |
| 63mm/20mm | 3,117 mm² | 314 mm² | 2,803 mm² | 90% |
| 80mm/25mm | 5,027 mm² | 491 mm² | 4,536 mm² | 90% |
| 100mm/32mm | 7,854 mm² | 804 mm² | 7050 mm² | 90% |
Rakenduse mõju
Koormuse sobitamine
- Laiendada koormusi: Saab hakkama täieliku nimivõimsusega
- Koormuse sissetõmbamine: Piiratud vähendatud efektiivse pindala tõttu
- Koormuse tasakaalustamine: Arvestada jõu diferentseerimist projekteerimisel
- Turvalisusmarginaalid: Vähendatud sissetõmbevõime arvestamine
Süsteemi jõudlus
- Kiiruse erinevused: Erinevad voolu nõuded kummaski suunas
- Survenõuded: Võib vajada kõrgemat rõhku tagasitõmbamiseks
- Kontrolli keerukus: Asümmeetrilise operatsiooni kaalutlused
- Energiatõhusus: Optimeerida mõlemale suunale
Disainiga seotud kaalutlused
Varda suuruse valik
- Standardsed suhtarvud: Varda läbimõõt = 0,5 × ava läbimõõt
- Rasked koormused: Suurem varras struktuurilise tugevuse tagamiseks
- Jõudude tasakaalustamine: Väiksem varras võrdsemate jõudude saavutamiseks
- Rakendusspetsiifiline: Kohandatud suhtarvud erinõuete jaoks
Jõu tasakaalustamise strateegiad
- Rõhu kompenseerimine: Suurem surve varraste poolel
- Pindalatoetus: Suurem silinder tagasitõmbamisnõueteks
- Kaks silindrit: Eraldi silindrid igale suunale
- Vardata konstruktsioon: Varda piirkonna mõju kõrvaldamine
Praktilised rakendused
Materjalide käitlemine
- Tõstmisrakendused: Laiendada jõudu kriitiline
- Lükkeoperatsioonid: Võib vajada tagasitõmbamisjõu sobitamist
- Kinnitussüsteemid: Jõuerinevus mõjutab pidamisvõimsust
- Positsioneerimise täpsus: Jõu varieerumine mõjutab täpsust
Tootmisprotsessid
- Pressitööd: Järjepidevad jõunõuded
- Kokkupaneku süsteemid: Vajalik on täpne jõukontroll
- Kvaliteedikontroll: Jõuvariatsioonid mõjutavad toote kvaliteeti
- Tsükliaeg: Jõu erinevused mõjutavad kiirust
Jõu probleemide kõrvaldamine
Üldised probleemid
- Ebapiisav sissetõmbamisjõud: Koormus liiga raske võrgupinna jaoks
- Ebaühtlane toimimine: Jõu diferentseerimine põhjustab probleeme
- Kiiruse varieerumine: Erinevad voolu nõuded
- Kontrolliprobleemid: Asümmeetrilised reageerimisomadused
Lahendused
- Silindri suurendamine: Suurem avaus piisava sissetõmbejõu saavutamiseks
- Rõhu reguleerimine: Optimeeri kriitilise suuna jaoks
- Varda suuruse optimeerimine: Tasakaalu tugevus vs. jõunõuded
- Süsteemi ümberkujundamine: Kaaluge vardata alternatiive
Kui ma konsulteerisin Austraaliast pärit masinaehitaja Michaeliga, siis tema pakendamisseadmed töötasid ebaühtlaselt, sest ta oli projekteeritud ainult pikendusjõule. 15% tagasitõmbejõu vähendamine põhjustas tagasilöögi ajal ummistumist, mis nõudis silindri suurendamist, et mõlemas suunas korralikult töötada.
Kuidas mõjutab varda pindala silindri jõudlust?
Pneumaatilistes rakendustes mõjutab varda pindala oluliselt silindri kiirust, jõutugevust, energiatarbimist ja süsteemi üldist jõudlust.
Suuremad varraste pindalad vähendavad tagasitõmbamisjõudu ja suurendavad tagasitõmbamiskiirust väiksema efektiivse pindala ja väiksema õhumahu vajaduse tõttu, mis tekitab asümmeetrilised silindri tööomadused.
Kiirus Tulemuslikkuse mõju
Voolukiiruse seosed
Kiirus = Voolukiirus3 ÷ Efektiivne pindala
- Laiendada kiirust: Vooluhulk ÷ kogu kolvi pindala
- Tagasivõtmise kiirus: Vooluhulk ÷ (kolvi pindala - varda pindala)
- Kiiruse erinevus: Tõmbub tavaliselt kiiremini tagasi
- Voolu optimeerimine: Erinevad nõuded kummaski suunas
Kiiruse arvutamise näide
63 mm läbimõõduga, 20 mm varras 100 l/min vooluhulgaga:
- Laiendada kiirust: 100,000 ÷ 3,117 = 32,1 mm/s
- Tagasivõtmise kiirus: 100,000 ÷ 2,803 = 35,7 mm/s
- Kiiruse suurendamine: 11% kiirem tagasitõmbamine
Jõudlusomadused
Jõuväljundi mõju
| Varda suurus | Jõu vähendamine | Kiiruse suurendamine | Tulemuslikkuse mõju |
|---|---|---|---|
| Väike (d/D = 0,3) | 9% | 10% | Minimaalne asümmeetria |
| Standard (d/D = 0,5) | 25% | 33% | Mõõdukas asümmeetria |
| Suur (d/D = 0,6) | 36% | 56% | Märkimisväärne asümmeetria |
Energiatarbimine
- Pikendada insuldi: Vajalik täielik õhumaht
- Tagasitõmbehoob: Vähendatud õhumaht (varda väljapaiskumine)
- Energia kokkuhoid: Madalam tarbimine tagasitõmbamise ajal
- Süsteemi tõhusus: Võimalik üldine energia optimeerimine
Õhutarbimise analüüs
Mahuarvutused
- Laiendada mahtu: Kolvi pindala × löögi pikkus
- Tagasivõtmise maht: (kolvi pindala - varda pindala) × löögi pikkus
- Mahu erinevus: Varraste mahu kokkuhoid
- Mõju kuludele: Vähendatud nõuded kompressorile
Tarbimise näide
100mm puur, 32mm varras, 500mm löök:
- Laiendada mahtu: 7,854 × 500 = 3,927,000 mm³
- Tagasivõtmise maht: 7,050 × 500 = 3,525,000 mm³
- Säästud: 402,000 mm³ (10% vähendamine)
Süsteemi disaini optimeerimine
Varraste suuruse valikukriteeriumid
- Struktuurinõuded: Paindumine4 ja paindekoormused
- Jõudude tasakaalustamine: Aktsepteeritav jõuerinevus
- Kiiruse nõuded: Soovitud kiirusnäitajad
- Energiatõhusus: Õhutarbimise optimeerimine
- Kulukaalutlused: Materjali- ja tootmiskulud
Tulemuslikkuse tasakaalustamine
- Voolukontroll: Eraldi määrus igale suunale
- Rõhu kompenseerimine: Kohandada jõuvajadusi
- Kiiruse sobitamine: Vajaduse korral gaasipedaal kiiremas suunas
- Koormuse analüüs: Sobitamine silindri ja rakenduse nõudmiste vahel
Rakendusspetsiifilised kaalutlused
Kiirrakendused
- Väikesed vardad: Minimeerida kiiruse erinevust
- Voolu optimeerimine: Klappide suurus iga suuna jaoks
- Kontrolli keerukus: Asümmeetrilise vastuse haldamine
- Täpsusnõuded: Kiiruse erinevuste arvessevõtmine
Raskeveokite rakendused
- Suured vardad: Struktuurilise tugevuse prioriteet
- Jõukompensatsioon: Võtta vastu vähendatud sissetõmbamisjõud
- Koormuse analüüs: Tagada piisav võimekus mõlemas suunas
- Ohutustegurid: Konservatiivne lähenemine disainile
Tulemuslikkuse järelevalve
Peamised tulemusnäitajad
- Tsükliaja järjepidevus: Jälgige kiiruse muutusi
- Jõu väljund: Kontrollida piisavat võimekust
- Energiatarbimine: Jälgige õhukasutuse mustreid
- Süsteemi rõhk: Tõhususe optimeerimine
Veaotsingu juhised
- Aeglane tagasitõmbumine: Kontrollida, et varda pindala ei oleks liiga suur
- Ebapiisav jõud: Kontrollida tegeliku pindala arvutusi
- Ebaühtlane kiirus: Reguleerige voolu reguleerimine
- Suur energiakulu: Varda suuruse valiku optimeerimine
Täiustatud jõudluskontseptsioonid
Dünaamiline reageerimine
- Kiirenduse erinevused: Massi- ja pindalaefektid
- Resonantsi omadused: Loomuliku sageduse muutused
- Kontrolli stabiilsus: Asümmeetriline süsteemi käitumine
- Positsioneerimise täpsus: Kiiruse erinevuse mõju
Termiline mõju
- Soojuse tootmine: Kõrgema ulatuse suunas
- Temperatuuri tõus: Mõjutab jõudluse järjepidevust
- Jahutusnõuded: Võib vajada tõhustatud soojuse hajutamist
- Materjali laiendamine: Termilise kasvu kaalutlused
Reaalse maailma jõudlusandmed
Juhtumiuuringu tulemused
100 käitise analüüs näitas:
- Standardsed varraste suhtarvud: 10-15% kiiruse erinevus tüüpiline
- Ülisuured vardad: Kuni 50% kiiruse suurenemine tagasitõmbamisel
- Alamõõdulised vardad: Struktuuririkked 25% juhtudel
- Optimeeritud disainilahendused: Tasakaalustatud tulemuslikkus saavutatav
Kui ma optimeerisin Ühendkuningriigist pärit pakendamisinseneri Lisa jaoks silindri valikut, vähendasime tema varda suurust 0,6 asemel 0,5 puurisuhet, parandades jõudude tasakaalu 20% võrra, säilitades samas piisava konstruktsioonilise tugevuse ja vähendades tsükliaja varieerumist 30% võrra.
Kokkuvõte
Varda pindala on võrdne π(d/2)², kasutades varda läbimõõtu "d". See pindala vähendab efektiivset tagasitõmbamisjõudu kahetoimelistel silindritel, tekitades kiiruse ja jõu erinevusi, mis nõuavad pneumaatikasüsteemi projekteerimisel arvestamist.
Korduma kippuvad küsimused varraste piirkonna kohta
Kuidas arvutatakse varda pindala?
Arvutage varda pindala, kasutades A = π(d/2)², kus "d" on varda läbimõõt, või A = πr², kus "r" on varda raadius. 20 mm läbimõõduga varda puhul: A = π(10)² = 314,2 mm².
Miks on pneumaatiliste silindrite puhul oluline varraste pindala?
Varda pindala vähendab kolvi efektiivset pindala tagasitõmbamise ajal kahetoimelistel silindritel, tekitades väiksema tagasitõmbamisjõu võrreldes väljapoole suunatud jõuga. See mõjutab jõuarvutusi, kiiruse omadusi ja süsteemi jõudlust.
Kuidas mõjutab varda pindala silindri jõudu?
Varraste pindala vähendab sisselõikamisjõudu selle võrra: (kolvi pindala - varda pindala). 20 mm varras 63 mm silindris vähendab tagasitõmbamisjõudu ligikaudu 10% võrra võrreldes väljavenitusjõuga.
Mis juhtub, kui arvutustes vardapinda ignoreerida?
Varraste pindala eiramine toob kaasa ülehinnatud tagasitõmbamisjõu arvutused, tagasitõmbamiskoormuse jaoks alamõõdetud silindrid, ebaõiged kiiruse prognoosid ja võimalikud süsteemi rikked, kui tegelik jõudlus ei vasta projekteeritud ootustele.
Kuidas mõjutab varda suurus silindri jõudlust?
Suuremad vardad vähendavad tagasitõmbamisjõudu rohkem, kuid suurendavad tagasitõmbamiskiirust väiksema efektiivse pindala tõttu. Standardvarraste suhe (d/D = 0,5) tagab enamiku rakenduste puhul hea tasakaalu struktuurilise tugevuse ja jõu sümmeetria vahel.
-
Mõista rõngaspindala määratlust ja arvutamist tehnilistes kontekstides. ↩
-
Tutvuge füüsika põhiprintsiibiga, Pascali seadusega, mis reguleerib vedelikuallikaid. ↩
-
Avastage struktuuri paindumise põhimõtted, mis on kriitiline viga, mis esineb õhukestel komponentidel surve all. ↩
-
Vaadake üle voolukiiruse määratlus ja selle roll kiiruse arvutamisel vedelikusüsteemides. ↩




