Millised on olulised pneumaatilise ülekande võrrandid, mida iga insener peaks teadma?

Kolmepaaniline tehniline infograafika, mis näitab olulisi pneumaatilisi võrrandeid. Esimene tahvel illustreerib ideaalgaasi seadust (PV = nRT) suletud gaasipaagi diagrammiga. Teisel paneelil selgitatakse jõu võrrandit (F = P × A) kolvi skeemi abil. Kolmandal paneelil on esitatud voolukiiruse seos (Q = v × A) koos toru kaudu liikuva õhu diagrammiga, kusjuures iga valemite muutuja on selgelt seotud vastava visuaalse elemendiga. — ideaalse gaasi seadus

Kas te olete pidevalt hädas pneumaatiliste süsteemide arvutustega? Paljud insenerid seisavad pneumaatiliste süsteemide projekteerimisel või tõrkeotsingul silmitsi sama probleemiga. Hea uudis on see, et mõne võtmevõrrandi valdamine võib lahendada enamiku teie pneumaatiliste süsteemide probleeme.

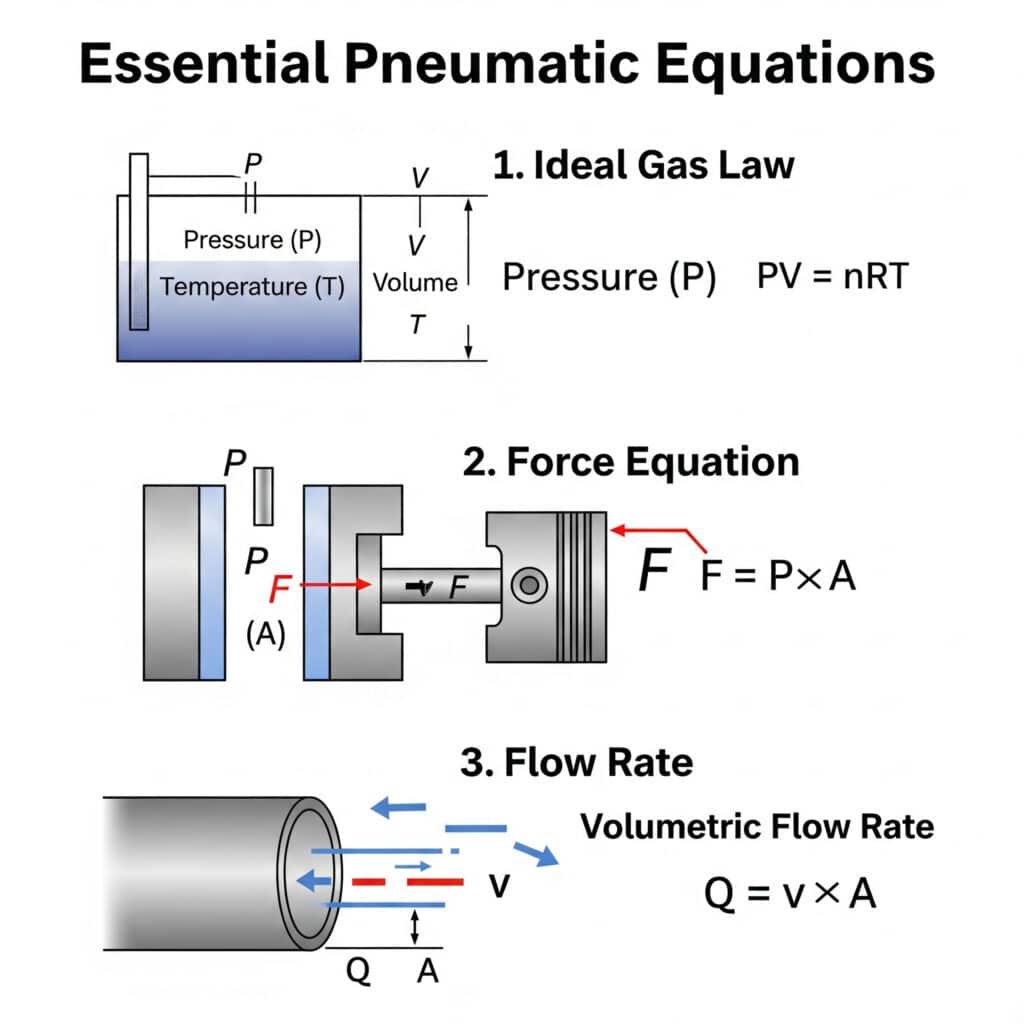
Olulised pneumaatilise jõuülekande võrrandid, mida iga insener peaks teadma, on järgmised. ideaalse gaasi seadus (PV = nRT)¹, jõu võrrand (F = P × A) ja voolukiiruse suhe (Q = v × A). Nende põhialuste mõistmine võimaldab süsteemi täpset projekteerimist ja tõrkeotsingut.

Olen Beptos töötanud üle 15 aasta pneumaatiliste süsteemidega ja olen omal nahal näinud, kuidas nende põhiliste võrrandite mõistmine võib säästa tuhandeid dollareid seisakute arvelt ja vältida kulukaid projekteerimisvigu.

Sisukord

Gaasi võrrandi tuletamine: Miks on PV = nRT oluline pneumaatilistes süsteemides?
Kuidas on jõud, rõhk ja pindala seotud pneumaatiliste balloonide puhul?
Milline on voolukiiruse ja kiiruse suhe pneumaatilistes süsteemides?
Kokkuvõte
Korduma kippuvad küsimused pneumaatilise ülekande võrranditest

Gaasi võrrandi tuletamine: Miks on PV = nRT oluline pneumaatilistes süsteemides?

Pneumaatiliste süsteemide projekteerimisel on oluline mõista, kuidas gaasid erinevates tingimustes käituvad. Need teadmised võivad teha vahet usaldusväärselt töötava süsteemi ja ootamatult rikki mineva süsteemi vahel.

Ideaalgaasi seadus (PV = nRT) on pneumaatiliste süsteemide puhul põhiline, sest see kirjeldab rõhu, mahu ja temperatuuri vastastikust mõju. See seos aitab inseneridel ennustada, kuidas õhk käitub varraseta balloonides ja muudes pneumaatilistes komponentides erinevates töötingimustes.

Tehniline diagramm, mis selgitab ideaalgaasi seadust. Sellel on kujutatud kinnine mahuti, mis kujutab fikseeritud "mahtu (V)". Mahutil olev mõõtur näitab rõhku (P) ja silt näitab temperatuuri (T). Valem "PV = nRT" on nähtavalt kujutatud, ühendades rõhu, mahu ja temperatuuri mõisted mahutis oleva gaasi jaoks. — Gaasiseaduse rakendused pneumaatikas

Ideaalse gaasi seadus võib tunduda teoreetilise kontseptsioonina füüsikatunnist, kuid sellel on otsene praktiline rakendus pneumaatikasüsteemides. Lubage mul seda praktilisemalt lahti mõtestada.

PV = nRT muutujate mõistmine

Muutuv	Tähendus	Pneumaatiline rakendus
P	Surve	Töörõhk teie süsteemis
V	Köide	Õhukambri suurus silindrites
n	Moolide arv	Õhukogus süsteemis
R	Gaasikonstant²	Universaalne konstant (8,314 J/mol-K)
T	Temperatuur	Töötemperatuur

Kuidas temperatuur mõjutab pneumaatilist jõudlust

Temperatuurivahetused võivad oluliselt mõjutada pneumosüsteemi jõudlust. Eelmisel aastal võttis üks meie klient Saksamaal, Hans, minuga ühendust oma vardata silindrisüsteemi ebajärjekindla jõudluse tõttu. Hommikul töötas süsteem ideaalselt, kuid pärastlõunal kaotas ta võimsuse.

Pärast tema seadistuse analüüsimist avastasime, et süsteem oli avatud otsesele päikesevalgusele, mis põhjustas temperatuuritõusu 15 °C. Ideaalse gaasiseaduse abil arvutasime, et see temperatuurimuutus põhjustas peaaegu 5% suurust rõhu muutust. Paigaldasime nõuetekohase isolatsiooni ja probleem lahenes kohe.

Gaasiseaduse praktilised rakendused pneumaatika projekteerimisel

Pneumaatiliste süsteemide projekteerimisel koos vardata silindrid, aitab meid gaasiseadus:

Arvutage temperatuuri kõikumisest tingitud rõhumuutusi.
Määrake kindlaks õhuvaru mahuvajadused
Prognoosida jõu väljundmuutusi erinevates tingimustes
Kompressorite suurus vastavalt rakendusele

Kuidas on jõud, rõhk ja pindala seotud pneumaatiliste balloonide puhul?

Jõu, rõhu ja pindala vahelise seose mõistmine on oluline, kui valite oma rakendusele sobiva vardata silindri. Need teadmised tagavad teile vajaliku jõudluse ilma liigsete kulutusteta.

The jõu, rõhu ja pindala suhe³ pneumosilindrite puhul on defineeritud järgmiselt: F = P × A, kus F on jõud (N), P on rõhk (Pa) ja A on efektiivne pindala (m²). See võrrand võimaldab inseneridel arvutada täpse jõu väljundi varraseta balloonide puhul erinevate töörõhkude korral.

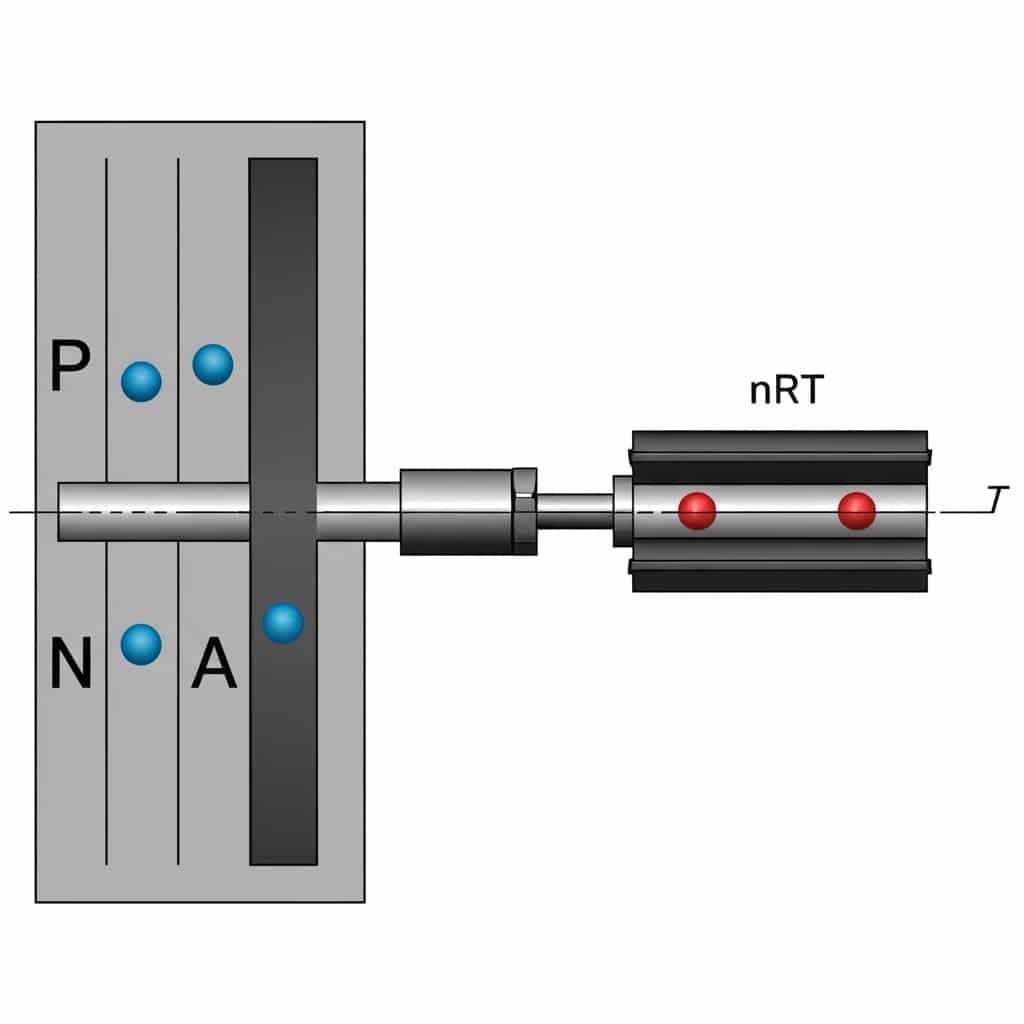
Tehniline skeem, mis illustreerib jõu arvutamist vardata pneumosilindris. Silindri kolbipindala on tähistatud "A" ja sisemine õhurõhk on tähistatud "P". Noolega on näidatud silindri poolt rakendatav jõud (F). Paremal on esitatud valem "F = P × A", mis näitab selgelt nende kolme muutuja vahelist seost. — Jõu arvutamine vardata silindrite puhul

See lihtne võrrand on kõigi pneumaatiliste jõudude arvutuste aluseks, kuid on mitmeid praktilisi kaalutlusi, mida paljud insenerid eiravad.

Efektiivse pindala arvutused erinevate silindertüüpide jaoks

Efektiivne pindala sõltub silindri tüübist:

Silindri tüüp	Efektiivse pindala arvutamine	Märkused
Ühetoimeline	A = πr²	Täispuurimisala
Kahepoolse toimega (pikendus)	A = πr²	Täispuurimisala
Kahepoolne toimimine (tagasitõmbamine)	A = π(r² - r'²)	r' on varraste raadius
Vardata silinder	A = πr²	Järjepidevus mõlemas suunas

Reaalse maailma jõu tõhususe tegurid

Praktikas mõjutavad tegelikku jõuväljundit:

Hõõrdekadu: Tavaliselt 3-20% sõltuvalt tihendi konstruktsioonist.
Rõhu langus: Võib vähendada efektiivset rõhku 5-10% võrra.
Dünaamilised efektid: Kiirendusjõud võivad vähendada olemasolevat jõudu

Mäletan, et töötasin koos Sarah'ga, kes oli ühe Ühendkuningriigi pakendiettevõtte mehaanikainsener. Ta kavandas uut masinat ja oli arvutanud, et vajas 63 mm läbimõõduga vardata silindrit, et saavutada vajalik jõud. Kuid ta ei olnud arvestanud hõõrdekadusid.

Soovitasime suurendada silindrit 80 mm läbimõõduga, mis andis piisavalt lisajõudu, et ületada hõõrdumine, säilitades samal ajal nõutava jõudluse. See lihtne kohandamine päästis ta pärast paigaldamist kulukast ümberehitusest.

Teoreetilise ja tegeliku jõuväljundi võrdlemine

Vardata silindrite valimisel soovitan alati:

Arvutage teoreetiline jõud, kasutades F = P × A
Enamiku rakenduste puhul kohaldatakse ohutustegurit 25%.
Kontrollida arvutusi tootja tegelike tulemuslikkuse andmete põhjal.
Vajaduse korral võtta arvesse dünaamilisi koormustingimusi

Milline on voolukiiruse ja kiiruse suhe pneumaatilistes süsteemides?

Voolukiirus ja kiirus on kriitilised parameetrid, mis määravad, kui kiiresti teie pneumosüsteem reageerib. Selle seose mõistmine aitab vältida aeglast tööd ja tagab, et teie süsteem vastab tsükliaegade nõuetele.

Suhted voolukiirus (Q) ja kiirus (v)⁴ pneumaatilistes süsteemides on määratletud valemiga Q = v × A, kus Q on ruumiline vooluhulk, v on õhu kiirus ja A on läbilaskekoha ristlõike pindala. See võrrand on oluline õhuliinide ja ventiilide õigeks dimensioneerimiseks.

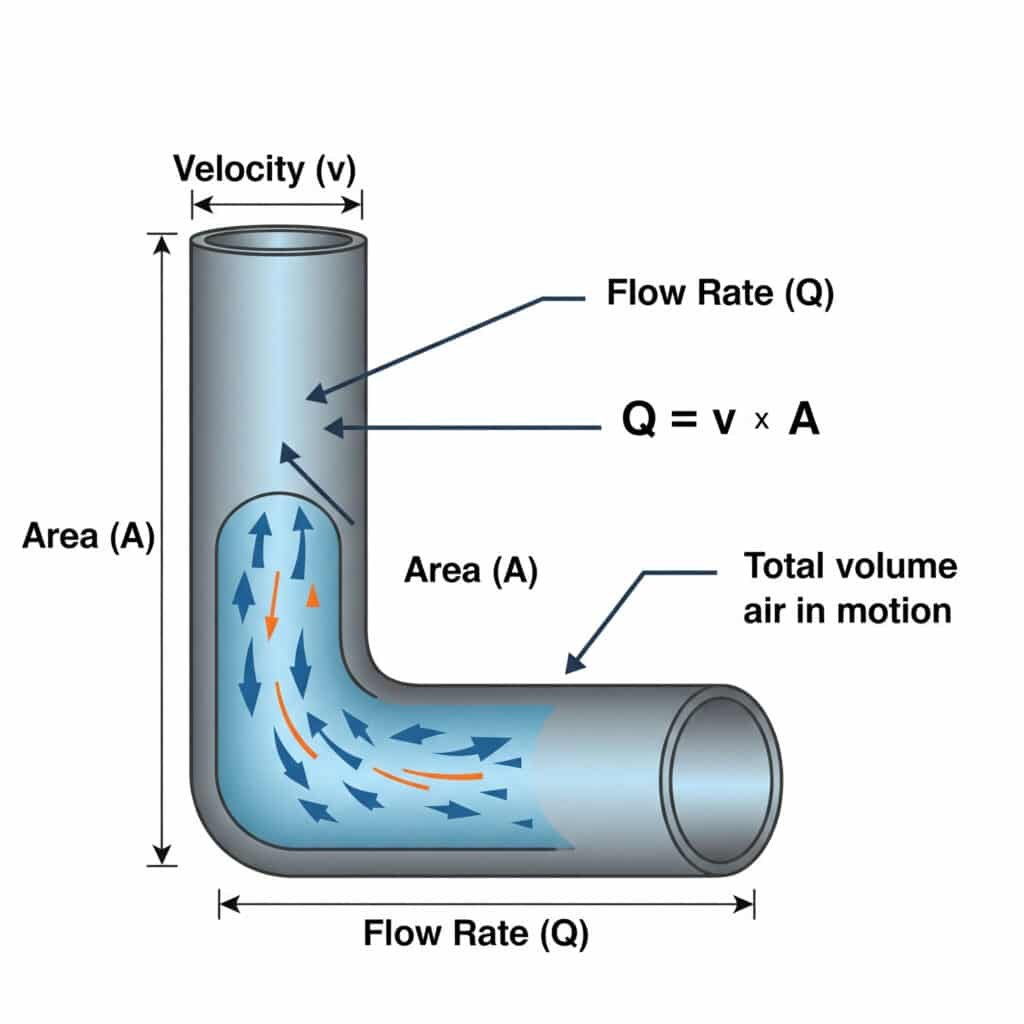
Tehniline diagramm, mis selgitab voolukiiruse, kiiruse ja pindala vahelist seost. Sellel on kujutatud sirge toru, mida läbib õhk. Õhu kiirus on näidatud noolega, millel on märge "Velocity (v)". Toru ümmargune ava on tähistatud pindalaga (A). Saadud koguvooluhulk on märgitud "vooluhulk (Q)". Valem "Q = v × A" on nähtavalt esitatud, kusjuures nooled ühendavad iga muutujat vastava elemendiga joonisel. — Voolukiiruse ja kiiruse suhe

Paljud pneumaatikasüsteemi probleemid tulenevad õhuvarustuse komponentide ebaõigest mõõtmest. Uurime, kuidas see võrrand mõjutab tegelikku toimivust.

Kriitilised vooluhulgad tavaliste pneumaatiliste komponentide jaoks

Erinevatel komponentidel on erinevad voolutamisnõuded:

Komponent	Tüüpiline voolukiiruse nõue	Alamõõdu mõju
Vardata silinder (25 mm läbimõõduga)	15-30 L/min	Aeglane töö, vähendatud jõud
Vardata silinder (63 mm läbimõõduga)	60-120 L/min	Ebajärjekindel liikumine
Suunaventiil	Varieerub suuruse järgi	Rõhu langus, aeglane reageerimine
Õhu ettevalmistusüksus	Süsteem kokku + 30%	Rõhu kõikumine

Kuidas toru läbimõõt mõjutab süsteemi jõudlust

Õhuliinide läbimõõt mõjutab oluliselt süsteemi jõudlust:

Rõhu langus: Suureneb koos kiiruse ruuduga
Reageerimisaeg: Väiksemad jooned tähendavad suuremat kiirust, kuid suuremat vastupanu.
Energiatõhusus: Suuremad liinid vähendavad rõhulangust, kuid suurendavad kulusid

Pneumaatiliste süsteemide õigete liinimõõtude arvutamine

Õhuliinide õigeks mõõtmiseks teie vardata silindri jaoks:

Vajaliku voolukiiruse määramine silindri suuruse ja tsükli kestuse alusel
Arvutage maksimaalne lubatud rõhulangus (tavaliselt 0,1 baari või vähem).
Valige liini läbimõõt, mis hoiab kiiruse alla 15-20 m/s.
Kontrollida ventiili läbilaskevõimet (Cv või Kv väärtus⁵) vastab süsteeminõuetele

Aitasin kord Prantsusmaal üht klienti, kellel oli aeglane ballooni liikumine, kuigi tal oli suur kompressor. Probleem ei olnud mitte ebapiisav õhutootmine, vaid see, et tema 6 mm torud tekitasid liigset vastupanu. Probleemi lahendas kohe 10 mm torustiku uuendamine, mis suurendas tema masina tsükli kiirust 40% võrra.

Kokkuvõte

Nende kolme põhilise pneumaatilise võrrandi - ideaalse gaasiseaduse, jõu, rõhu ja pindala suhte ning voolukiiruse ja voolukiiruse vahelise seose - mõistmine on aluseks edukale pneumaatilise süsteemi projekteerimisele. Neid põhimõtteid rakendades saate valida õiged vardata balloonikomponendid, lahendada tõhusalt probleeme ja optimeerida süsteemi jõudlust.

Korduma kippuvad küsimused pneumaatilise ülekande võrranditest

Mis on ideaalgaasi seadus ja miks on see pneumaatiliste süsteemide puhul oluline?

Ideaalse gaasi seadus (PV = nRT) kirjeldab, kuidas rõhk, ruumala, temperatuur ja gaasi kogus on pneumaatilises süsteemis omavahel seotud. See on oluline, sest see aitab inseneridel ennustada, kuidas muutuvad tingimused (eriti temperatuur) mõjutavad süsteemi jõudlust ja rõhunõudeid.

Kuidas arvutada vardata silindri jõu väljundit?

Arvutage väljundjõud, korrutades rõhu efektiivse pindalaga (F = P × A). Vardata silindri puhul on efektiivne pindala mõlemas suunas ühesugune, mis muudab jõuarvutused lihtsamaks kui tavaliste silindrite puhul, millel on erinevad välja- ja sissetõmbamisjõud.

Mis vahe on vooluhulga ja kiiruse vahel pneumaatikasüsteemides?

Voolukiirus on süsteemi läbiv õhumaht ajaühikus (tavaliselt l/min), samas kui kiirus on kiirus, millega õhk liigub läbi süsteemi (m/s). Need on seotud võrrandiga Q = v × A, kus A on läbilaskekoha ristlõike pindala.

Kuidas mõjutab temperatuur pneumosüsteemi jõudlust?

Ideaalse gaasiseaduse kohaselt mõjutab temperatuur otseselt rõhku. Temperatuuri tõus 10 °C võib suurendada rõhku ligikaudu 3,5% võrra, kui ruumala jääb samaks. See võib põhjustada rõhu muutusi, mõjutada tihendite toimivust ja muuta jõu väljundit vardata balloonides.

Mis on pneumaatiliste süsteemide rõhulanguse kõige tavalisem põhjus?

Kõige sagedasemad rõhulanguse põhjused on alamõõdulised õhuliinid, piiravad liitmikud ja ebapiisav klapi vooluvõimsus. Vastavalt vooluhulga võrrandile nõuavad väiksemad kanalid suuremat õhukiirust, mis suurendab vastupanu ja rõhulangust eksponentsiaalselt.

Kuidas mõõdan õhuliinid õigesti vardata silindri jaoks?

Õhuliinide suuruse määramiseks arvutage vajalik voolukiirus silindri mahu ja tsükli kestuse põhjal ning valige seejärel toru läbimõõt, mis hoiab õhu kiiruse alla 15-20 m/s, et vähendada rõhulangust. Enamiku vardata balloonide rakenduste puhul on 8-12 mm õhuliinid hea tasakaalus jõudluse ja kulude vahel.

Selgitab üksikasjalikult ideaalse gaasiseadust, mis on hüpoteetilise ideaalse gaasi põhiline olekuvõrrand, mis lähendab paljude gaaside käitumist erinevates tingimustes. ↩
Selgitab universaalse gaasikonstandi (R) rolli ja väärtust ideaalgaasi seaduses, mis on füüsikaline konstant, mis seob energia skaala ja temperatuuri skaala. ↩
Pakub põhilisi selgitusi rõhu kohta, mis on määratletud kui objekti pinnale risti mõjuv jõud pindalaühiku kohta, millele see jõud on jaotatud. ↩
Üksikasjalikult käsitletakse pidevuse võrrandi põhimõtet, mis on vedelikudünaamika põhikontseptsioon, mille kohaselt kokkusurutamatu vedeliku puhul peab massivoolukiirus olema konstantne toru ühest ristlõikest teise. ↩
Annab vooluteguri (Cv) ja vooluteguri (Kv) tehnilise määratluse, mis on standardiseeritud väärtused, mida kasutatakse erinevate ventiilide vooluvõimsuse võrdlemiseks. ↩

Tere, ma olen Chuck, vanemekspert, kellel on 15-aastane kogemus pneumaatikatööstuses. Bepto Pneumaticus keskendun kvaliteetsete ja kohandatud pneumaatiliste lahenduste pakkumisele meie klientidele. Minu teadmised hõlmavad tööstusautomaatikat, pneumaatikasüsteemide projekteerimist ja integreerimist, samuti võtmekomponentide rakendamist ja optimeerimist. Kui teil on küsimusi või soovite arutada oma projekti vajadusi, võtke minuga ühendust aadressil chuck@bepto.com.