Miten männän kinematiikka vaikuttaa pneumaattisen järjestelmän suorituskykyyn?

CQ2-sarjan kompaktin pneumaattisen sylinterin asennussarjat

Onko sinulla ongelmia epäjohdonmukaisten pneumaattisten sylinterien nopeuksien tai odottamattomien iskujen kanssa? Nämä yleiset ongelmat johtuvat usein männän kinematiikan huonosta ymmärtämisestä. Monet insinöörit keskittyvät pelkästään voimavaatimuksiin ja jättävät huomiotta kriittiset liikeparametrit, jotka määrittävät järjestelmän suorituskyvyn.

Männän kinematiikka¹ vaikuttavat suoraan pneumaattisen järjestelmän suorituskykyyn paineen ja nopeuden suhteiden, kiihtyvyysrajojen ja pehmustevaatimusten kautta. Näiden periaatteiden ymmärtämisen avulla insinöörit voivat mitoittaa komponentit oikein, ennustaa todelliset liikeprofiilit ja estää sauvattomien sylintereiden ja muiden pneumaattisten toimilaitteiden ennenaikaiset viat.

Yli 15 vuotta Beptolla pneumaattisten järjestelmien parissa työskennellessäni olen nähnyt lukemattomia tapauksia, joissa näiden perusperiaatteiden ymmärtäminen on auttanut asiakkaita ratkaisemaan pysyviä suorituskykyongelmia ja pidentämään laitteiden käyttöikää 3-5 kertaa.

Sisällysluettelo

Millaista painetta tarvitset oikeastaan vakionopeusliikkeeseen?
Miten lasketaan suurin mahdollinen kiihtyvyys pneumaattisissa sylintereissä?
Miksi puskuriajalla on merkitystä ja miten se lasketaan?
Päätelmä
Usein kysytyt kysymykset mäntäkinematiikasta pneumaattisissa järjestelmissä

Millaista painetta tarvitset oikeastaan vakionopeusliikkeeseen?

Monet insinöörit käyttävät pneumaattisissa järjestelmissään vain suurinta mahdollista painetta, mutta tämä lähestymistapa on tehoton ja voi johtaa nykivään liikkeeseen, liialliseen kulumiseen ja energian tuhlaamiseen.

Pneumaattisen sylinterin vakionopeusliikkeeseen tarvittava paine lasketaan kaavalla P = (F + Fr)/A, jossa P on paine, F on ulkoinen kuormitusvoima, Fr on kitkavastus ja A on männän pinta-ala. Tämä laskutapa takaa tasaisen ja tehokkaan toiminnan ilman liiallista painetta, joka tuhlaa energiaa ja nopeuttaa komponenttien kulumista.

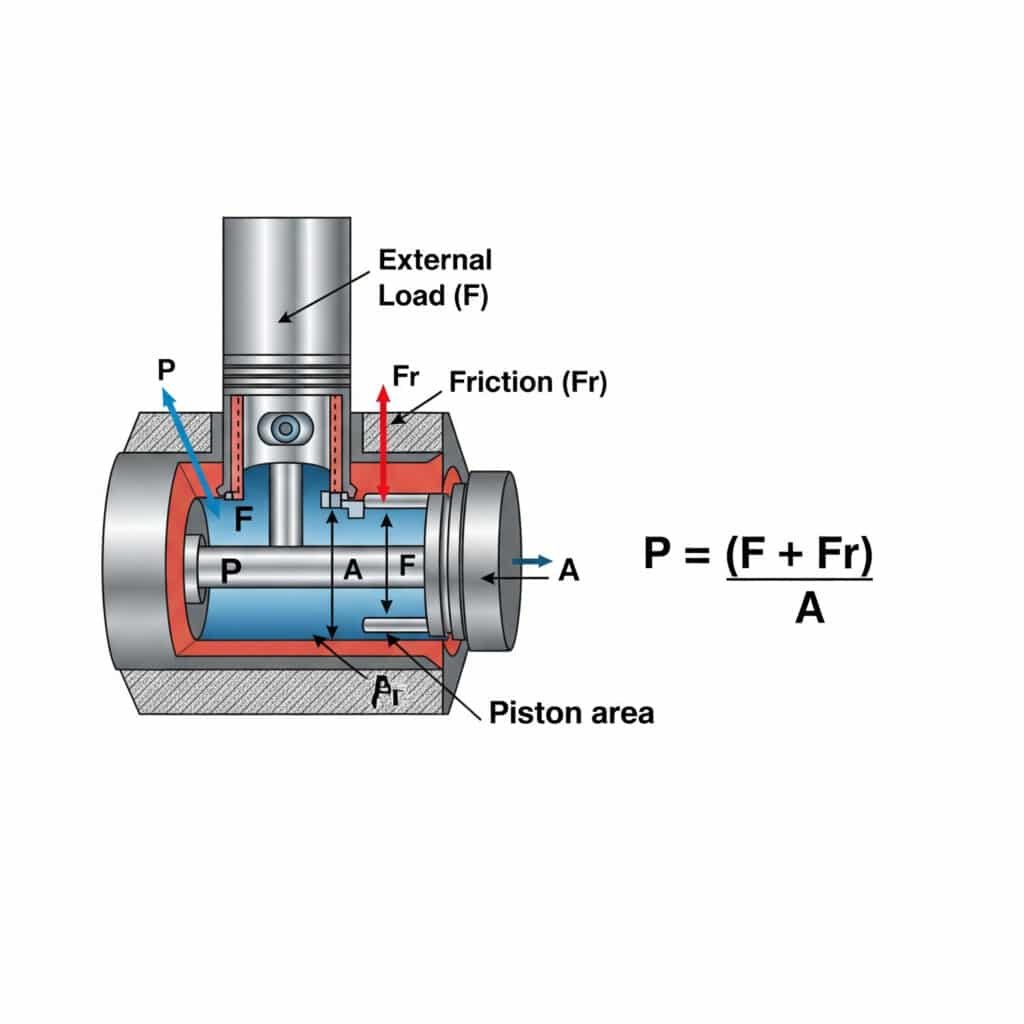
Tekninen vapaakappalekaavio, jossa selitetään pneumaattisen sylinterin paineen laskeminen. Siinä on poikkileikkaus sylinteristä, joka työntää lohkoa, joka on merkitty merkinnällä "Ulkoinen kuorma (F)". Nuoli osoittaa vastakkaisen kitkan (Fr). Sisäpuolella oleva paine on merkitty merkinnällä "P", ja se vaikuttaa männän pinta-alaan (A). Kaava "P = (F + Fr)/A" esitetään näkyvästi, ja nuolet yhdistävät kunkin muuttujan vastaavaan voimaan tai ominaisuuteen kaaviossa. — Vakionopeuspaineen laskentakaavio

Vakionopeusliikkeen painevaatimusten ymmärtämisellä on käytännön vaikutuksia järjestelmän suunnitteluun ja toimintaan. Jaottelen tämän käytännönläheisiksi oivalluksiksi.

Vakionopeuden painevaatimuksiin vaikuttavat tekijät

Vakionopeuden ylläpitämiseen tarvittava paine riippuu useista tekijöistä:

Tekijä	Vaikutus painevaatimukseen	Käytännön näkökohtia
Ulkoinen kuormitus	Suora lineaarinen suhde	Vaihtelee suuntautumisen ja ulkoisten voimien mukaan
Kitka	Lisää vaadittua painetta	Muutokset tiivisteen kulumisen ja voitelun myötä
Mäntäalue	Kääntäen verrannollinen	Suurempi läpivienti = pienempi painevaatimus
Ilmansyöttörajoitukset	Painehäviöt linjoissa/venttiileissä	Komponenttien mitoitus minimaalista painehäviötä varten
Vastapaine	Vastustaa esitystä	Huomioi pakokaasun virtauskapasiteetti

Vakaan liikkeen edellyttämän vähimmäispaineen laskeminen

Määritetään vakaan liikkeen edellyttämä vähimmäispaine:

Laske ulkoisen kuormituksen voittamiseen tarvittava voima.
Lisätään kitkavoima (tyypillisesti 3-20% maksimivoimasta).
Jaetaan männän tehollisella pinta-alalla
Lisätään vakauskerroin (tyypillisesti 10-30%).

Esimerkiksi 40 mm:n läpimittaisessa sauvattomassa sylinterissä, jossa on 10 kg:n kuorma ja 15%:n kitka:

Parametri	Laskenta	Tulos
Kuormitusvoima	10kg × 9,81m/s²	98.1N
Kitkavoima	15% maksimivoima 6 baarin paineessa	~45N
Kokonaisvoima	98,1N + 45N	143.1N
Mäntäalue	π × (0,02m)²	0.00126m²
Vähimmäispaine	143.1N ÷ 0.00126m²	113 571 Pa (1,14 bar)
20%:n kanssa vakaustekijä	1,14 bar × 1,2	1,37 bar

Todellisen maailman sovellus: Paineoptimointi: Energiansäästö

Viime vuonna työskentelin Robertin kanssa, joka oli tuotantoinsinööri Michiganissa sijaitsevassa huonekalutehtaassa. Hänen automatisoidulla kokoonpanolinjallaan käytettiin sauvattomia sylintereitä, jotka toimivat täydellä 6 baarin syöttöpaineella kuormituksesta riippumatta.

Analysoituamme hänen sovellustaan totesimme, että useimmat liikkeet vaativat vain 2,5-3 baaria vakaaseen toimintaan. Asentamalla proportionaaliset paineensäätimet, vähensimme ilman kulutusta 40%:llä samalla syklin keston pysyessä samana. Tämä säästi vuosittain noin $12 000 energiakustannuksia ja vähensi samalla tiivisteiden kulumista ja pidensi huoltovälejä.

Nopeuden ja paineen suhde todellisissa järjestelmissä

Käytännössä paineen ja nopeuden välinen suhde ei ole täysin lineaarinen seuraavista syistä:

Virtausrajoitukset: Venttiilin ja portin mitoitus vaikuttaa suurimpaan saavutettavissa olevaan nopeuteen.
Puristuvuusvaikutukset: Ilma on kokoonpuristuvaa, mikä aiheuttaa kiihtyvyysviiveen.
Stick-slip-ilmiöt: Kitkaominaisuudet muuttuvat nopeuden mukaan
Inertiavaikutukset: Massan kiihtyvyys vaatii lisävoimaa/paineita

Miten lasketaan suurin mahdollinen kiihtyvyys pneumaattisissa sylintereissä?

Kiihtyvyysrajojen ymmärtäminen on ratkaisevan tärkeää, jotta voidaan estää liiallinen isku, tärinä ja komponenttien ennenaikainen vikaantuminen pneumaattisissa järjestelmissä.

Suurin mahdollinen kiihtyvyys pneumaattisessa sylinterissä lasketaan käyttäen a = (P × A - F - Fr)/m, jossa a on kiihtyvyys, P on paine, A on männän pinta-ala, F on ulkoinen kuormitus, Fr on kitkavastukset ja m on liikkuva massa. Tämä yhtälö määrittelee fyysiset rajat sille, kuinka nopeasti pneumaattinen toimilaite voi käynnistää tai pysäyttää liikkeen.

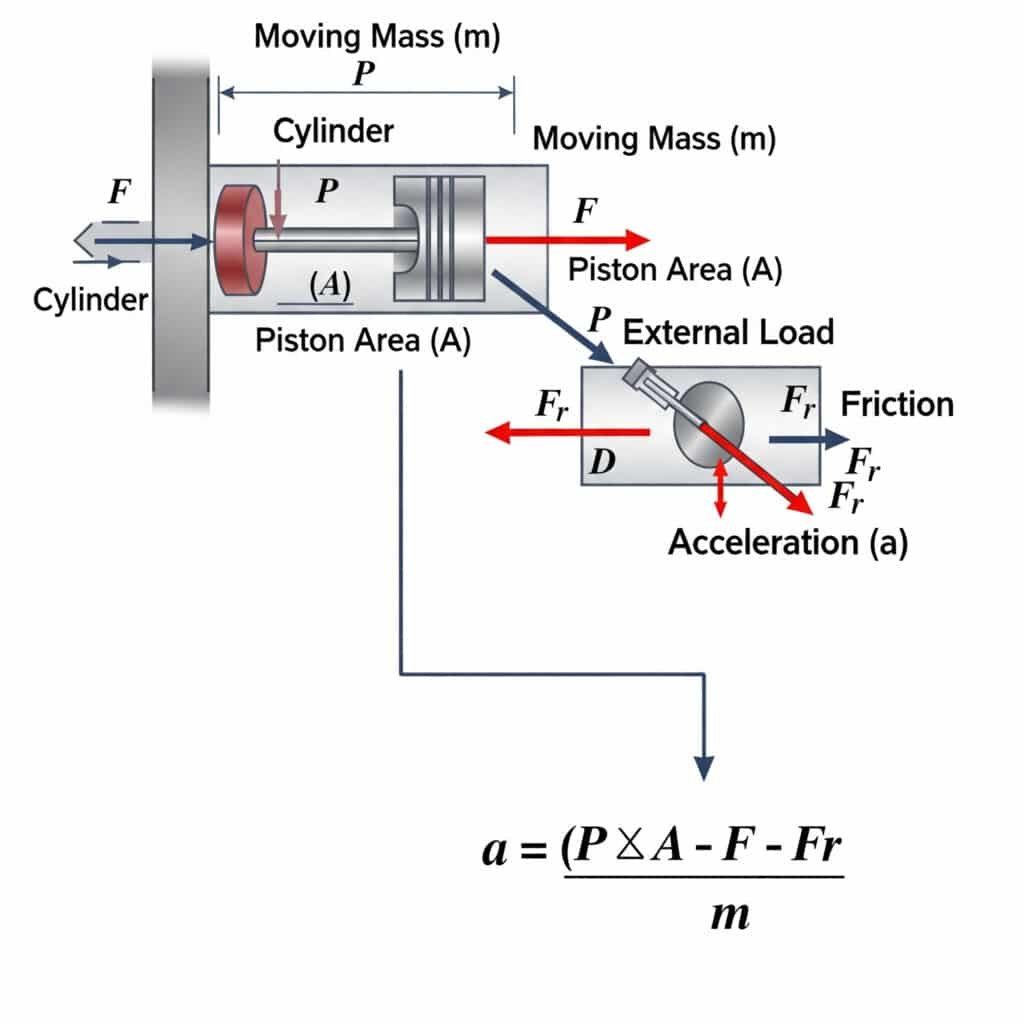
Tekninen vapaakappalekaavio, jossa selitetään pneumaattisen sylinterin kiihtyvyyden laskenta. Kuvassa on sylinteri, joka työntää lohkoa, jonka kohdalla on merkintä "Liikkuva massa (m)". Suuri nuoli osoittaa 'Paineen (P)' tuottaman käyttövoiman 'männän alueelle (A)'. Tätä vastapäätä on kaksi pienempää nuolta, joissa on merkinnät 'Ulkoinen kuorma (F)' ja 'Kitka (Fr)'. Suuri nuoli osoittaa tuloksena syntyvän kiihtyvyyden (a). Kaava "a = (P × A - F - Fr)/m" on näkyvästi esillä, ja kukin muuttuja on yhdistetty vastaavaan elementtiin kaaviossa. — Kiihtyvyysrajan johdannaiskaavio

Teoreettisilla kiihtyvyysrajoilla on merkittäviä käytännön vaikutuksia järjestelmän suunnitteluun ja komponenttien valintaan.

Kiihtyvyyden raja-arvoyhtälön johtaminen

Kiihtyvyyden raja-arvoyhtälö saadaan seuraavasta yhtälöstä Newtonin toinen laki² (F = ma):

Kiihtyvyyteen käytettävissä oleva nettovoima on: Fnet = Fpaine - Fload - Ffriction.
Fpaine = P × A
Siis: a = Fnet/m = (P × A - F - Fr)/m.

Käytännön kiihtyvyysrajat eri sylinterityypeille

Eri sylinterimalleilla on erilaiset käytännön kiihtyvyysrajat:

Sylinterin tyyppi	Tyypillinen enimmäiskiihtyvyys	Rajoittavat tekijät
Vakiotankosylinteri	10-15 m/s²	Sauvan vääntyminen, laakerikuormat
Sauvaton sylinteri (magneettinen)	8-12 m/s²	Magneettisen kytkennän vahvuus
Sauvaton sylinteri (mekaaninen)	15-25 m/s²	Tiivisteen/laakerin rakenne, sisäinen kitka
Ohjaussylinteri	20-30 m/s²	Ohjausjärjestelmän jäykkyys, kantavuus
Iskusylinteri	50-100+ m/s²	Suunniteltu erityisesti suurta kiihtyvyyttä varten

Massan huomioon ottaminen kiihtyvyyslaskelmissa

Kiihtyvyyttä laskettaessa on tärkeää ottaa huomioon kaikki liikkuvat massat:

Männän kokoonpano: Sisältää männän, tiivisteet ja liitososat.
Kuorman massa: Siirrettävä ulkoinen kuorma
Liikkuvan ilman tehollinen massa: Usein vähäinen, mutta merkityksellinen suurnopeussovelluksissa.
Kiinnitysosien aiheuttama lisämassa: Kannattimet, anturit jne.

Autoin kerran ranskalaista asiakasta, jolla oli mystisiä vikoja sauvattomassa sylinterijärjestelmässään. Sylinteri oli mitoitettu oikein ilmoitetulle 15 kg:n kuormitukselle, mutta se vioittui jatkuvasti muutaman tuhannen syklin jälkeen.

Tutkittuamme asiaa huomasimme, että hän ei ollut ottanut huomioon kiinnityslevyn ja kiinnikkeiden 12 kg:n massaa. Todellinen liikkuva massa oli lähes kaksinkertainen laskettuun verrattuna, mikä aiheutti kiihtyvyysvoimia, jotka ylittivät sylinterin suunnittelurajat. Kun sylinteri oli päivitetty suurempaan sylinteriin, viat loppuivat kokonaan.

Kiihdytyksen ohjausmenetelmät

Kiihtyvyyden hallitseminen turvallisissa rajoissa:

Virtauksen säätöventtiilit: Virtausnopeuden rajoittaminen alkuliikkeen aikana
Suhteelliset venttiilit: Tarjoaa hallitun paineen nousun
Monivaiheinen kiihdytys: Käytä asteittaista paineen nousua
Mekaaninen vaimennus: Lisää ulkoiset iskunvaimentimet
Elektroninen ohjaus: Käytä servopneumaattiset järjestelmät³ kiihtyvyyspalautteella

Miksi puskuriajalla on merkitystä ja miten se lasketaan?

Asianmukainen iskun lopun pehmentäminen on olennaisen tärkeää iskuvaurioiden estämiseksi, melun vähentämiseksi ja pneumaattisten sylintereiden käyttöiän pidentämiseksi. Tyynyttämisajan ymmärtäminen auttaa insinöörejä suunnittelemaan järjestelmiä, joissa syklien kesto ja komponenttien pitkäikäisyys ovat tasapainossa.

Pneumaattisten sylintereiden vaimennusaika lasketaan yhtälöllä t = √(2s/a), jossa t on aika, s on vaimennuksen iskun pituus ja a on hidastuvuus. Tämä aika kuvaa sitä, kuinka kauan liikkuvan massan turvallinen hidastaminen ennen törmäystä kestää, mikä on ratkaisevan tärkeää sylinterin ja siihen liitettyjen osien vaurioitumisen estämiseksi.

Tekninen infografiikka, jossa selitetään pneumaattisen iskunvaimennuksen ajan laskeminen. Siinä on suurennettu poikkileikkaus männästä, joka tulee sylinterin päässä olevaan pehmusteeseen. Mittaviiva osoittaa "iskunvaimennuksen keston (s)", kun taas suuri vastakkainen nuoli edustaa "hidastuvuutta (a)". Sekuntikellokuvake havainnollistaa 'Pehmitysaikaa (t)'. Kaava "t = √(2s/a)" on näkyvästi esillä, ja nuolet yhdistävät kunkin muuttujan vastaavaan elementtiin kaaviossa. — Kiihtyvyysrajan johdannaiskaavio

Tutustutaan pehmentävän ajan laskennan käytännön näkökohtiin ja niiden vaikutuksiin järjestelmän suunnittelussa.

Fysiikka pneumaattisen pehmusteen takana

Pneumaattinen pehmuste toimii ilman hallitun puristuksen ja rajoitetun pakokaasun avulla:

Kun mäntä tulee puskurikammioon, pakokaasuputki on rajoitettu.
Loukkuun jäänyt ilma puristuu, jolloin vastapaine kasvaa.
Tämä vastapaine luo vastavoiman, joka hidastaa mäntää.
Hidastuvuusprofiili riippuu tyynyn rakenteesta ja säädöstä.

Optimaalisen vaimennusaikojen laskeminen

Optimaalinen vaimennusaika tasapainottaa iskujen ehkäisyn ja syklin tehokkuuden:

Parametri	Kaava	Esimerkki
Pehmustuksen etäisyys	Sylinterin rakenteen perusteella	15 mm (tyypillinen 40 mm:n poraus)
Vaadittu hidastuvuus	a = v²/(2s)	Kun v=0,5m/s, s=15mm: a = 8,33m/s².
Pehmustusaika	t = √(2s/a)	t = √(2×0,015/8,33) = 0,06s.
Paineen muodostuminen	P = P₀(V₀/V)^γ	Riippuu tyynykammion geometriasta

Pehmusteiden suorituskykyyn vaikuttavat tekijät

Useat tekijät vaikuttavat pehmusteiden todelliseen suorituskykyyn:

Tyynytiivisteen rakenne: Vaikuttaa ilmavuotoon pehmusteiden pehmustuksen aikana.
Neulaventtiilin säätö: Säätää pakokaasun rajoitusastetta
Liikkuva massa: Raskaammat kuormat vaativat pidemmän pehmitysajan.
Lähestymisnopeus: Suuremmat nopeudet vaativat pidemmän pehmusteiden etäisyyden
Käyttöpaine: Vaikuttaa käytettävissä olevaan suurimpaan vastavoimaan

Pehmustetyypit ja niiden sovellukset

Erilaiset vaimennusmekanismit soveltuvat eri sovelluksiin:

Tyynyn tyyppi	Ominaisuudet	Parhaat sovellukset
Kiinteä pehmuste	Yksinkertainen, ei-säädettävä	Kevyet kuormat, johdonmukainen toiminta
Säädettävä pehmuste	Viritettävissä neulaventtiileillä	Vaihtelevat kuormat, joustavat sovellukset
Itsesäätyvä pehmuste	Sopeutuu erilaisiin olosuhteisiin	Muuttuvat nopeudet ja kuormat
Ulkoiset iskunvaimentimet	Korkea energian absorptio	Raskaat kuormat, suuret nopeudet
Elektroninen pehmuste	Tarkasti ohjattu hidastaminen	Servopneumaattiset järjestelmät

Tapaustutkimus: Pehmusteiden optimointi korkean syklin sovelluksissa

Työskentelin hiljattain Thomasin kanssa, joka on suunnitteluinsinööri saksalaisessa autoteollisuuden komponenttivalmistajassa. Hänen kokoonpanolinjallaan käytettiin sauvattomia sylintereitä, jotka toimivat 45 syklin minuutissa, mutta niissä esiintyi usein tiivistevikoja ja kiinnityskorvakkeiden vaurioita.

Analyysi osoitti, että pehmitysaika oli liian lyhyt liikkuvaan massaan nähden, mikä aiheutti lähes 3 prosentin iskuvoimia iskun kummassakin päässä. Lisäämällä iskunvaimennuksen iskua 12 mm:stä 20 mm:iin ja optimoimalla neulaventtiilin asetukset pidensimme iskunvaimennusaikaa 0,04 s:sta 0,07 s:aan.

Tämä näennäisen pieni muutos vähensi iskuvoimia yli 60%:llä, poisti kiinnikkeen vaurioitumisen kokonaan ja pidensi tiivisteen käyttöikää kolmesta kuukaudesta yli vuoteen - kaikki tämä säilyttäen vaaditun syklin keston.

Käytännön pehmusteiden säätömenettely

Optimaalisen pehmustustehon saavuttamiseksi sauvattomissa sylintereissä:

Käynnistä pehmusteventtiilit täysin auki (pienin mahdollinen rajoitus).
Sulje pehmusteventtiili asteittain, kunnes saavutetaan tasainen hidastuvuus.
Testi pienimmällä ja suurimmalla odotetulla kuormituksella
Tarkista pehmustusteho koko nopeusalueella.
Kuuntele iskuääniä, jotka viittaavat riittämättömään pehmusteeseen.
Mittaa todellinen hidastumisaika laskelmien vahvistamiseksi.

Päätelmä

Mäntäkinematiikan periaatteiden ymmärtäminen - vakionopeutta koskevista painevaatimuksista kiihtyvyysrajoihin ja pehmitysajan laskelmiin - on olennaista tehokkaiden ja luotettavien pneumaattisten järjestelmien suunnittelussa. Soveltamalla näitä periaatteita sauvattomiin sylinterisovelluksiisi voit optimoida suorituskyvyn, vähentää energiankulutusta ja pidentää komponenttien käyttöikää merkittävästi.

Usein kysytyt kysymykset mäntäkinematiikasta pneumaattisissa järjestelmissä

Minkälainen paine tarvitaan tiettyä sylinterin nopeutta varten?

Tarvittava paine riippuu kuormituksesta, kitkasta ja sylinterin pinta-alasta. Laske se käyttämällä P = (F + Fr)/A, jossa F on ulkoinen kuormitusvoima, Fr on kitkavastus ja A on männän pinta-ala. Tyypillisessä sauvattomassa sylinterissä, joka liikuttaa 10 kg:n painoista kuormaa vaakasuorassa, tarvitaan noin 1,5-2 baaria vakaaseen liikkeeseen kohtuullisilla nopeuksilla.

Kuinka nopeasti pneumaattinen sylinteri voi kiihtyä?

Pneumaattisen sylinterin maksimikiihtyvyys lasketaan käyttämällä arvoa a = (P × A - F - Fr)/m. Tyypilliset sauvattomat sylinterit voivat saavuttaa 10-25 m/s² kiihtyvyyden rakenteesta riippuen. Tämä tarkoittaa 0,5 m/s nopeuden saavuttamista noin 20-50 millisekunnissa optimaalisissa olosuhteissa.

Mitkä tekijät rajoittavat sauvattoman sylinterin enimmäisnopeutta?

Maksiminopeutta rajoittavat venttiilin virtauskapasiteetti, ilmansyöttötilavuus, aukkojen mitoitus, pehmusteominaisuudet ja tiivisteen rakenne. Useimmat vakiomalliset sauvattomat sylinterit on suunniteltu 0,8-1,5 m/s enimmäisnopeuksille, mutta erikoistuneet nopeat mallit voivat saavuttaa 2-3 m/s.

Miten lasken sopivan pehmusteen sovellukselleni?

Laske asianmukainen pehmuste määrittämällä liikkuvan kuorman liike-energia (KE = ½mv²) ja varmistamalla, että pehmustejärjestelmä pystyy absorboimaan tämän energian. Pehmusteaika on laskettava käyttämällä t = √(2s/a), jossa s on pehmusteen etäisyys ja a on haluttu hidastuvuusnopeus.

Mitä tapahtuu, jos pneumaattinen sylinterini kiihtyy liian nopeasti?

Liiallinen kiihtyvyys voi aiheuttaa mekaanista rasitusta kiinnityskomponentteihin, tiivisteiden ennenaikaista kulumista, lisääntynyttä tärinää ja melua, mahdollista kuorman siirtymistä tai vaurioitumista sekä järjestelmän tarkkuuden heikkenemistä. Se voi myös johtaa nykivään liikkeeseen, joka vaikuttaa tuotteen laatuun tarkkuussovelluksissa.

Miten kuorman suuntaus vaikuttaa liikkumiseen tarvittavaan paineeseen?

Kuorman suuntaus vaikuttaa merkittävästi painevaatimuksiin. Painovoimaa vastaan liikkuvat pystysuorat kuormat vaativat lisäpainetta painovoiman voittamiseksi (P = F/A + Fg/A + Fr/A). Vaakakuormien on voitettava vain kitka ja inertia. Kaltevat kuormat sijoittuvat näiden ääripäiden väliin kulman sinin perusteella.

Tarjoaa perustavanlaatuisen selityksen kinematiikasta, mekaniikan haarasta, joka kuvaa kappaleiden liikettä ottamatta huomioon liikkeen aiheuttavia voimia.
elektroninen tulosignaali, joka mahdollistaa kehittyneen pneumaattisen ohjauksen. ↩
Newtonin toinen laki (F=ma) on fysiikan perusperiaate, joka suhteuttaa kappaleeseen vaikuttavan voiman sen massaan ja kiihtyvyyteen ja joka on kaikkien dynaamisten laskelmien perusta. ↩
Kuvaa servopneumatiikkaa, kehittynyttä ohjaustekniikkaa, jossa yhdistyvät pneumatiikan teho ja suljetun silmukan elektronisen ohjauksen tarkkuus erittäin tarkkojen paikannus- ja liikeprofiilien saavuttamiseksi. ↩

Hei, olen Chuck, vanhempi asiantuntija, jolla on 15 vuoden kokemus pneumatiikka-alalta. Bepto Pneumaticilla keskityn tuottamaan asiakkaillemme laadukkaita, räätälöityjä pneumatiikkaratkaisuja. Asiantuntemukseni kattaa teollisuusautomaation, pneumatiikkajärjestelmien suunnittelun ja integroinnin sekä avainkomponenttien soveltamisen ja optimoinnin. Jos sinulla on kysyttävää tai haluat keskustella projektitarpeistasi, ota rohkeasti yhteyttä minuun osoitteessa chuck@bepto.com.