Insinöörit laskevat usein sauvojen pinta-alat väärin suunnitellessaan pneumaattisia sylinterijärjestelmiä, mikä johtaa virheellisiin voimalaskelmiin ja järjestelmän toimintahäiriöihin.
Sauvan pinta-ala on ympyränmuotoinen poikkipinta-ala, joka lasketaan kaavalla A = πr² tai A = π(d/2)², jossa "r" on sauvan säde ja "d" on sauvan halkaisija, joka on kriittinen voima- ja painelaskelmien kannalta.
Autoin eilen Carlosia, meksikolaista suunnitteluinsinööriä, jonka pneumaattinen järjestelmä epäonnistui, koska hän unohti vähentää männän pinta-alan tangon pinta-alasta kaksitoimisen sylinterin voiman laskelmissa.
Sisällysluettelo
- Mikä on pneumaattisten sylinterijärjestelmien sauva-alue?
- Miten lasketaan sauvan poikkileikkauspinta-ala?
- Miksi sauvan pinta-ala on tärkeä voiman laskennassa?
- Miten sauvan pinta-ala vaikuttaa sylinterin suorituskykyyn?
Mikä on pneumaattisten sylinterijärjestelmien sauva-alue?
Männän pinta-ala edustaa männänvarren ympyränmuotoista poikkileikkauspinta-alaa, joka on olennainen laskettaessa männän tehollista pinta-alaa ja voimantuottoa kaksitoimisissa pneumaattisissa sylintereissä.
Sauvan pinta-ala on männänvarren poikkileikkauksen täyttämä ympyränmuotoinen pinta-ala, joka mitataan kohtisuoraan sauvan akseliin nähden ja jota käytetään tehollisen nettopinta-alan määrittämiseen voimalaskelmia varten.
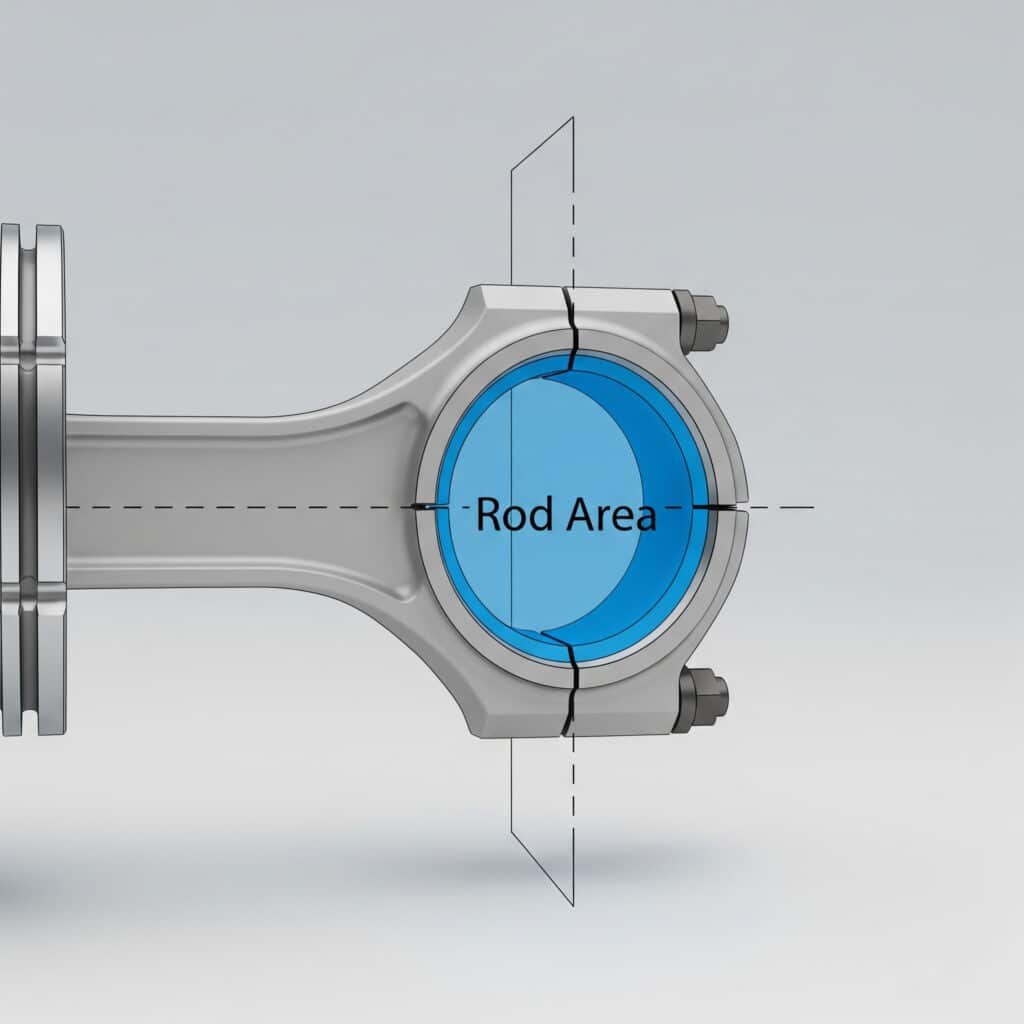
Sauvan alueen määritelmä
Geometriset ominaisuudet
- Pyöreä poikkileikkaus: Standardi sauvageometria
- Kohtisuora mittaus: 90° tangon keskilinjaan nähden
- Vakiopinta-ala: Tasainen sauvan pituussuunnassa
- Kiinteä alue: Materiaalin täydellinen poikkileikkaus
Tärkeimmät mittaukset
- Sauvan halkaisija: Pinta-alan laskennassa käytettävä ensisijainen ulottuvuus
- Sauvan säde: Puolet halkaisijan mittauksesta
- Poikkipinta-ala: Ympyränmuotoisen alueen kaavan soveltaminen
- Tehokas alue: Vaikutus sylinterin suorituskykyyn
Tangon ja männän pinta-alan suhde
| Komponentti | Alueen kaava | Käyttötarkoitus | Hakemus |
|---|---|---|---|
| Mäntä | A = π(D/2)² | Täysimittainen alue | Laajenna voiman laskentaa |
| Rod | A = π(d/2)² | Sauvan poikkileikkaus | Takaisinvetovoiman laskeminen |
| Nettopinta-ala | A_mäntä - A_tanko | Tehokas sisäänvedettävä alue | Kaksitoimiset sylinterit |
| Rengasmainen alue1 | π(D² - d²)/4 | Rengasmainen alue | Sauvapuolen paine |
Vakiotankojen koot
Yleiset tangon halkaisijat
- 8mm tanko: Pinta-ala = 50,3 mm²
- 12mm tanko: Pinta-ala = 113,1 mm²
- 16mm tanko: Pinta-ala = 201,1 mm²
- 20mm tanko: Pinta-ala = 314,2 mm²
- 25mm tanko: Pinta-ala = 490,9 mm²
- 32mm tanko: Pinta-ala = 804,2 mm²
Tangon ja reiän välinen suhde
- Vakiosuhde: Tangon halkaisija = 0,5 × reiän halkaisija
- Raskas kuormitus: Tangon halkaisija = 0,6 × reiän halkaisija
- Kevyt käyttö: Tangon halkaisija = 0,4 × reiän halkaisija
- Mukautetut sovellukset: Vaihtelee vaatimusten mukaan
Sauvan alueen sovellukset
Voiman laskelmat
Käytän sauva-aluetta:
- Pidentää voimaa: Koko männän pinta-ala × paine
- Takaisinvetovoima: (männän pinta-ala - sauvan pinta-ala) × paine
- Voimaero: Pidentämisen ja peruuttamisen välinen ero
- Kuormitusanalyysi: Sylinterin sovittaminen sovellukseen
Järjestelmän suunnittelu
Sauvan alue vaikuttaa:
- Sylinterin valinta: Oikea mitoitus sovelluksia varten
- Nopeuslaskelmat: Kunkin suunnan virtausvaatimukset
- Painevaatimukset: Järjestelmän painetta koskevat tiedot
- Suorituskyvyn optimointi: Tasapainotettu toimintamalli
Tangon pinta-ala eri sylinterityypeissä
Yksitoimiset sylinterit
- Ei vaikutusta sauvan pinta-alaan: Jousipalautustoiminto
- Ainoastaan pidentävä voima: Koko männän alue tehokas
- Yksinkertaistetut laskelmat: Takaisinvetovoimaa ei oteta huomioon
- Kustannusten optimointi: Vähennetty monimutkaisuus
Kaksitoimiset sylinterit
- Sauvan alue kriittinen: Vaikuttaa sisäänvetovoimaan
- Epäsymmetrinen toiminta: Eri voimat kumpaankin suuntaan
- Monimutkaiset laskelmat: Molemmat alueet on otettava huomioon
- Suorituskyvyn tasapainottaminen: Tarvittavat suunnitteluun liittyvät näkökohdat
Sauvattomat sylinterit
- Ei sauva-aluetta: Poistettu suunnittelusta
- Symmetrinen toiminta: Yhtä suuret voimat molempiin suuntiin
- Yksinkertaistetut laskelmat: Yhden alueen tarkastelu
- Tilan edut: Ei tangon pidennysvaatimuksia
Miten lasketaan sauvan poikkileikkauspinta-ala?
Sauvan poikkipinta-alan laskennassa käytetään standardia ympyränmuotoisen pinta-alan laskentakaavaa, jossa käytetään sauvan halkaisijan tai säteen mittauksia, jotta pneumaattisen järjestelmän suunnittelu olisi tarkkaa.
Laske sauvan pinta-ala käyttämällä A = πr² (säteen tapauksessa) tai A = π(d/2)² (halkaisijan tapauksessa), jossa π = 3,14159, varmistaen, että yksiköt ovat yhdenmukaiset koko laskennan ajan.
Perusalueen kaava
Sauvan säteen käyttäminen
A = πr²
- A: Sauvan poikkipinta-ala
- π: 3.14159 (matemaattinen vakio)
- r: Sauvan säde (halkaisija ÷ 2)
- Yksiköt: Pinta-ala säteen neliöyksikköinä
Sauvan halkaisijan käyttäminen
A = π(d/2)² tai A = πd²/4
- A: Sauvan poikkipinta-ala
- π: 3.14159
- d: Sauvan halkaisija
- Yksiköt: Pinta-ala halkaisijan neliöyksikköinä
Vaiheittainen laskenta
Mittausprosessi
- Mittaa tangon halkaisija: Käytä mittasaksia tarkkuuden varmistamiseksi
- Tarkista mittaus: Ota useita lukemia
- Laske säder = halkaisija ÷ 2 (jos käytetään säteen kaavaa).
- Käytä kaavaa: A = πr² tai A = π(d/2)².
- Tarkista yksiköt: Varmistetaan johdonmukainen yksikköjärjestelmä
Laskentaesimerkki
Halkaisijaltaan 20 mm:n sauvalle:
- Menetelmä 1: A = π(10)² = π × 100 = 314,16 mm².
- Menetelmä 2: A = π(20)²/4 = π × 400/4 = 314,16 mm².
- Tarkastus: Molemmat menetelmät antavat identtiset tulokset
Sauvojen pinta-alan laskentataulukko
| Sauvan halkaisija | Sauvan säde | Pinta-alan laskeminen | Sauvojen alue |
|---|---|---|---|
| 8mm | 4mm | π × 4² | 50,3 mm² |
| 12mm | 6mm | π × 6² | 113,1 mm² |
| 16mm | 8mm | π × 8² | 201,1 mm² |
| 20mm | 10mm | π × 10² | 314,2 mm² |
| 25mm | 12.5mm | π × 12.5² | 490,9 mm² |
| 32mm | 16mm | π × 16² | 804,2 mm² |
Mittaustyökalut
Digitaaliset kaliperit
- Tarkkuus±0,02 mm tarkkuus
- Valikoima: 0-150mm tyypillinen
- Ominaisuudet: Digitaalinen näyttö, yksikkömuunnos
- Paras käytäntö: Useita mittauspisteitä
Mikrometri
- Tarkkuus±0,001 mm tarkkuus
- Valikoima: Saatavana eri kokoja
- Ominaisuudet: Ratsiopastin, digitaaliset vaihtoehdot
- Sovellukset: Korkean tarkkuuden vaatimukset
Yleiset laskuvirheet
Mittausvirheet
- Halkaisija vs. säde: Väärän ulottuvuuden käyttäminen kaavassa
- Yksikön epäjohdonmukaisuus: Sekoittaminen mm ja tuumaa
- Tarkkuusvirheet: Ei riittävästi desimaaleja
- Työkalun kalibrointi: Kalibroimattomat mittauslaitteet
Kaavavirheet
- Väärä kaava: Ympärysmitan käyttäminen pinta-alan sijasta
- Puuttuva π: Unohdetaan matemaattinen vakio
- Virheiden neliöinti: Virheellinen eksponentin käyttö
- Yksikkömuunnos: Virheelliset yksikkömuunnokset
Tarkastusmenetelmät
Ristiintaulukointitekniikat
- Useita laskutoimituksia: Erilaiset kaavatekniikat
- Mittauksen todentaminen: Toista halkaisijan mittaukset
- Vertailutaulukot: Vertaa vakioarvoihin
- CAD-ohjelmisto: 3D-mallin pinta-alan laskelmat
Kohtuullisuustarkastukset
- Koon korrelaatio: Suurempi halkaisija = suurempi pinta-ala
- Vakiovertailut: Vastaavat tyypillisiä sauvakokoja
- Soveltuvuus: Sopii sylinterin kokoon
- Valmistusstandardit: Yleiset saatavilla olevat koot
Edistyneet laskelmat
Onttoja sauvoja
A = π(D² - d²)/4
- D: Ulkohalkaisija
- d: Sisähalkaisija
- Hakemus: Painon vähentäminen, sisäinen reititys
- Laskenta: Vähennä sisäinen alue ulkoisesta alueesta
Ei-ympyränmuotoiset sauvat
- Nelikulmaiset tangot: A = puoli²
- Suorakulmaiset tangot: A = pituus × leveys
- Erikoismuodot: Käytä sopivia geometrisia kaavoja
- Sovellukset: Estä kierto, erityisvaatimukset
Kun työskentelin kanadalaisen pneumaattisen järjestelmän suunnittelijan Jenniferin kanssa, hän laski aluksi sauvan pinta-alan väärin käyttämällä πr²-kaavassa halkaisijaa säteen sijasta, mikä johti 4-kertaiseen yliarviointiin ja täysin vääriin voimalaskelmiin hänen kaksitoimisen sylinterin sovelluksessaan.
Miksi sauvan pinta-ala on tärkeä voiman laskennassa?
Tangon pinta-ala vaikuttaa suoraan kaksitoimisten sylintereiden tangon puoleiseen mäntään, mikä aiheuttaa voimaeroja ulos- ja sisäänvedon välillä.
Tangon pinta-ala pienentää männän tehollista pinta-alaa sisäänvedon aikana, mikä aiheuttaa pienemmän sisäänvetovoiman kuin ulosvetovoima kaksitoimisissa sylintereissä, mikä edellyttää kompensaatiota järjestelmän suunnittelussa.
Voiman laskennan perusteet
Voiman peruskaava
- Pidentää voimaa: F = P × A_mäntä
- Takaisinvetovoima: F = P × (A_mäntä - A_tanko)
- Voimaero: Ulosvetovoima > sisäänvetovoima
- Suunnittelun vaikutus: On otettava huomioon molemmat suunnat
Tehokkaat alueet
- Koko männän alue: Käytettävissä laajentamisen aikana
- Männän nettopinta-ala: Männän pinta-ala miinus tangon pinta-ala sisäänvedon aikana.
- Rengasmainen alue: Rengasmainen alue tangon puolella
- Pinta-alan suhde: Määrittää voimaeron
Voiman laskenta Esimerkkejä
63mm reikä, 20mm tankosylinteri
- Männän pinta-ala: π(31.5)² = 3,117 mm².
- Tangon alue: π(10)² = 314 mm².
- Nettopinta-ala: 3,117 - 314 = 2,803 mm².
- 6 baarin paineessa:
– Pidentää voimaa: 6 × 3,117 = 18,702 N
– Takaisinvetovoima: 6 × 2,803 = 16,818 N
– Voimaero: 1,884 N (10% vähennys)
Voiman vertailutaulukko
| Sylinterin koko | Mäntäalue | Sauvojen alue | Nettopinta-ala | Voimasuhde |
|---|---|---|---|---|
| 32mm/12mm | 804 mm² | 113 mm² | 691 mm² | 86% |
| 50mm/16mm | 1,963 mm² | 201 mm² | 1,762 mm² | 90% |
| 63mm/20mm | 3,117 mm² | 314 mm² | 2,803 mm² | 90% |
| 80mm/25mm | 5,027 mm² | 491 mm² | 4,536 mm² | 90% |
| 100mm/32mm | 7,854 mm² | 804 mm² | 7,050 mm² | 90% |
Sovelluksen vaikutus
Kuormituksen sovittaminen
- Kuormien pidentäminen: Kestää täyden nimellisvoiman
- Vedä kuormat sisään: Rajoittuu pienentyneestä tehollisesta pinta-alasta
- Kuormituksen tasaus: Huomioi voimaero suunnittelussa
- Turvamarginaalit: Vähentynyt sisäänvetokyky on otettava huomioon
Järjestelmän suorituskyky
- Nopeuserot: Erilaiset virtausvaatimukset kumpaankin suuntaan
- Painevaatimukset: Saattaa tarvita korkeampaa painetta sisäänvedossa
- Valvonnan monimutkaisuus: Epäsymmetristä toimintaa koskevat näkökohdat
- Energiatehokkuus: Optimoi molempiin suuntiin
Suunnittelua koskevat näkökohdat
Sauvakoon valinta
- Vakiosuhteet: Tangon halkaisija = 0,5 × reiän halkaisija
- Raskaat kuormat: Suurempi tanko rakenteellisen lujuuden vuoksi
- Voimatasapaino: Pienempi tanko tasaisempien voimien aikaansaamiseksi
- Sovelluskohtainen: Räätälöidyt suhdeluvut erityisvaatimuksia varten
Voiman tasapainottamisstrategiat
- Paineen kompensointi: Suurempi paine sauvan puolella
- Aluekorvaus: Suurempi sylinteri vetäytymisvaatimuksia varten
- Kaksi sylinteriä: Erilliset sylinterit kutakin suuntaa varten
- Sauvaton rakenne: Poistaa sauva-alueen vaikutukset
Käytännön sovellukset
Materiaalin käsittely
- Nostosovellukset: Pidentää voimaa kriittisesti
- Työntöoperaatiot: Saattaa tarvita vetäytymisvoiman sovittamista
- Kiristysjärjestelmät: Voimaero vaikuttaa pitovoimaan
- Paikannustarkkuus: Voiman vaihtelut vaikuttavat tarkkuuteen
Valmistusprosessit
- Lehdistön toiminta: Yhdenmukaiset voimavaatimukset
- Kokoonpanojärjestelmät: Tarvitaan tarkkaa voimanohjausta
- Laadunvalvonta: Voiman vaihtelut vaikuttavat tuotteen laatuun
- Syklin kesto: Voimaerot iskunopeus
Force-ongelmien vianmääritys
Yleiset ongelmat
- Riittämätön sisäänvetovoima: Kuorma liian raskas verkkoalueelle
- Epätasainen toiminta: Voimaero aiheuttaa ongelmia
- Nopeuden vaihtelut: Erilaiset virtausvaatimukset
- Valvontaongelmat: Epäsymmetriset vasteominaisuudet
Ratkaisut
- Sylinterin suurentaminen: Suurempi reikä riittävää sisäänvetovoimaa varten
- Paineen säätö: Optimoi kriittinen suunta
- Sauvakoon optimointi: Tasapainovoima vs. voimavaatimukset
- Järjestelmän uudelleensuunnittelu: Harkitse sauvattomia vaihtoehtoja
Kun konsultoin Michaelia, australialaista koneenrakentajaa, hänen pakkauslaitteistonsa toimi epäjohdonmukaisesti, koska hän oli suunnitellut sen vain ojennusvoimaa varten. 15%:n sisäänvetovoiman vähentäminen aiheutti jumittumista paluuvirtauksen aikana, mikä vaati sylinterin suurentamista, jotta molempiin suuntiin voitaisiin toimia kunnolla.
Miten sauvan pinta-ala vaikuttaa sylinterin suorituskykyyn?
Tangon pinta-ala vaikuttaa merkittävästi sylinterin nopeuteen, voimantuottoon, energiankulutukseen ja järjestelmän kokonaissuorituskykyyn pneumaattisissa sovelluksissa.
Suuremmat sauvojen pinta-alat pienentävät sisäänvetovoimaa ja lisäävät sisäänvetonopeutta pienemmän tehollisen pinta-alan ja pienemmän ilmamäärävaatimuksen vuoksi, mikä johtaa sylinterin epäsymmetrisiin suorituskykyominaisuuksiin.
Nopeus Suorituskyky Vaikutus
Virtausnopeuden suhteet
Nopeus = Virtausnopeus3 ÷ Tehollinen pinta-ala
- Pidentää nopeutta: Virtaus ÷ männän koko pinta-ala
- Sisäänvedon nopeus: Virtaus ÷ (männän pinta-ala - sauvan pinta-ala)
- Nopeuserot: Vedä sisään tyypillisesti nopeammin
- Virtauksen optimointi: Eri vaatimukset kumpaankin suuntaan
Nopeuden laskentaesimerkki
63 mm:n poraus, 20 mm:n tanko 100 l/min virtauksella:
- Pidentää nopeutta: 100 000 ÷ 3,117 = 32,1 mm/s.
- Sisäänvedon nopeus: 100,000 ÷ 2,803 = 35,7 mm/s.
- Nopeuden kasvu: 11% nopeampi sisäänveto
Suorituskykyominaisuudet
Voiman lähtövaikutukset
| Sauvan koko | Voimien vähentäminen | Nopeuden lisäys | Suorituskyvyn vaikutus |
|---|---|---|---|
| Pieni (d/D = 0,3) | 9% | 10% | Vähäinen epäsymmetria |
| Standardi (d/D = 0,5) | 25% | 33% | Kohtalainen epäsymmetria |
| Suuri (d/D = 0,6) | 36% | 56% | Merkittävä epäsymmetria |
Energiankulutus
- Pidentää aivohalvausta: Tarvitaan täysi ilmamäärä
- Takaisinvetoisku: Pienennetty ilmamäärä (sauvan syrjäytys)
- Energiansäästöt: Pienempi kulutus sisäänvedon aikana
- Järjestelmän tehokkuus: Kokonaisenergian optimointi mahdollista
Ilman kulutuksen analysointi
Tilavuuslaskelmat
- Laajenna äänenvoimakkuutta: Männän pinta-ala × iskun pituus
- Vedä tilavuus sisään: (männän pinta-ala - sauvan pinta-ala) × iskun pituus
- Tilavuusero: Säästöt tangon tilavuudessa
- Kustannusvaikutus: Pienemmät kompressorivaatimukset
Kulutus Esimerkki
100 mm:n poraus, 32 mm:n tanko, 500 mm:n isku:
- Laajenna äänenvoimakkuutta: 7,854 × 500 = 3,927,000 mm³.
- Vedä tilavuus sisään: 7 050 × 500 = 3 525 000 mm³.
- Säästöt: 402,000 mm³ (10% vähennys)
Järjestelmän suunnittelun optimointi
Sauvakoon valintaperusteet
- Rakenteelliset vaatimukset: Taivutus4 ja taivutuskuormat
- Voimatasapaino: Hyväksyttävä voimaero
- Nopeusvaatimukset: Halutut nopeusominaisuudet
- Energiatehokkuus: Ilman kulutuksen optimointi
- Kustannusnäkökohdat: Materiaali- ja valmistuskustannukset
Suorituskyvyn tasapainottaminen
- Virtauksen säätö: Kullekin suunnalle erillinen asetus
- Paineen kompensointi: Säädä voimantarpeen mukaan
- Nopeuden sovittaminen: Tarvittaessa kaasu nopeampaan suuntaan
- Kuormitusanalyysi: Sovita sylinteri sovelluksen vaatimuksiin
Sovelluskohtaiset näkökohdat
Suurnopeussovellukset
- Pienet tangot: Minimoi nopeuserot
- Virtauksen optimointi: Venttiilien koko kutakin suuntaa varten
- Valvonnan monimutkaisuus: Epäsymmetrisen vasteen hallinta
- Tarkkuusvaatimukset: Nopeuden vaihteluiden huomioon ottaminen
Raskaan kaluston sovellukset
- Suuret tangot: Rakenteellisen lujuuden prioriteetti
- Voiman kompensointi: Hyväksy alennettu sisäänvetovoima
- Kuormitusanalyysi: Varmistetaan riittävät valmiudet molempiin suuntiin
- Turvallisuustekijät: Konservatiivinen lähestymistapa suunnitteluun
Suorituskyvyn seuranta
Keskeiset suorituskykyindikaattorit
- Syklien keston johdonmukaisuus: Seuraa nopeuden vaihteluita
- Voiman ulostulo: Varmista riittävä toimintakyky
- Energiankulutus: Seuraa ilman käyttötapoja
- Järjestelmän paine: Optimoi tehokkuus
Vianmääritysohjeet
- Hidas vetäytyminen: Tarkista, ettei sauvan pinta-ala ole liian suuri
- Riittämätön voima: Tarkista tehollisen pinta-alan laskelmat
- Epätasaiset nopeudet: Säädä virtauksen säätimet
- Suuri energiankulutus: Optimoi sauvakoon valinta
Kehittyneet suorituskykykäsitteet
Dynaaminen vaste
- Kiihtyvyyserot: Massa- ja aluevaikutukset
- Resonanssiominaisuudet: Luonnollisen taajuuden vaihtelut
- Ohjauksen vakaus: Epäsymmetrinen järjestelmäkäyttäytyminen
- Paikannustarkkuus: Nopeuserojen vaikutukset
Lämpövaikutukset
- Lämmöntuotanto: Korkeammalle ulottumissuunnassa
- Lämpötilan nousu: Vaikuttaa suorituskyvyn johdonmukaisuuteen
- Jäähdytysvaatimukset: Saattaa tarvita tehostettua lämmöntuottoa
- Materiaalin laajeneminen: Lämpökasvuun liittyvät näkökohdat
Todellisen maailman suorituskykytiedot
Tapaustutkimuksen tulokset
100 laitoksen analyysi osoitti:
- Vakiovarsien suhteet: 10-15% nopeusero tyypillinen
- Ylisuuret sauvat: Jopa 50%:n nopeuslisäys sisäänvedettäessä.
- Alimitoitetut sauvat: Rakenteellisia vikoja 25%:ssä tapauksista.
- Optimoidut mallit: Tasapainoinen suorituskyky saavutettavissa
Kun optimoin sylinterin valinnan Lisalle, Yhdistyneestä kuningaskunnasta kotoisin olevalle pakkausinsinöörille, pienensimme hänen sauvakokoa 0,6:sta 0,5:een, mikä paransi voimatasapainoa 20%:llä, mutta säilytti samalla riittävän rakenteellisen lujuuden ja vähensi syklien keston vaihtelua 30%:llä.
Päätelmä
Sauvan pinta-ala on π(d/2)², kun käytetään sauvan halkaisijaa d. Tämä pinta-ala pienentää tehokasta sisäänvetovoimaa kaksitoimisissa sylintereissä, mikä aiheuttaa nopeus- ja voimaeroja, jotka on otettava huomioon pneumatiikkajärjestelmän suunnittelussa.
Usein kysytyt kysymykset sauva-alueesta
Miten lasketaan tangon pinta-ala?
Lasketaan sauvan pinta-ala käyttäen A = π(d/2)², jossa "d" on sauvan halkaisija, tai A = πr², jossa "r" on sauvan säde. Halkaisijaltaan 20 mm:n sauva: A = π(10)² = 314,2 mm².
Miksi sauvan pinta-ala on tärkeä pneumaattisissa sylintereissä?
Tangon pinta-ala pienentää männän tehollista pinta-alaa kaksitoimisten sylintereiden sisäänvedon aikana, jolloin sisäänvetovoima on pienempi kuin ulosvetovoima. Tämä vaikuttaa voimalaskelmiin, nopeusominaisuuksiin ja järjestelmän suorituskykyyn.
Miten tangon pinta-ala vaikuttaa sylinterivoimaan?
Tangon pinta-ala pienentää sisäänvetovoimaa kyseisellä määrällä: (männän pinta-ala - sauvan pinta-ala). 20 mm:n tanko 63 mm:n sylinterissä vähentää sisäänvetovoimaa noin 10% verrattuna ulosvetovoimaan.
Mitä tapahtuu, jos laskelmissa ei oteta huomioon sauvan pinta-alaa?
Sauvojen pinta-alan huomiotta jättäminen johtaa yliarvioituihin vetovoimalaskelmiin, liian pieniin sylintereihin vetokuormia varten, virheellisiin nopeusennusteisiin ja mahdollisiin järjestelmävirheisiin, kun todellinen suorituskyky ei vastaa suunnittelun odotuksia.
Miten sauvakoko vaikuttaa sylinterin suorituskykyyn?
Suuremmat sauvat vähentävät vetovoimaa enemmän mutta lisäävät vetonopeutta pienemmän tehollisen pinta-alan ansiosta. Vakiovarsien suhteet (d/D = 0,5) tarjoavat hyvän tasapainon rakenteellisen lujuuden ja voiman symmetrian välillä useimmissa sovelluksissa.
-
Ymmärtää rengasmaisen alueen määritelmän ja laskennan teknisissä yhteyksissä. ↩
-
Tutustu fysiikan perusperiaatteeseen, Pascalin lakiin, joka ohjaa nestevoimajärjestelmiä. ↩
-
Tutustu rakenteellisen vääntymisen periaatteisiin, joka on kriittinen vikaantumistapa puristuksessa oleville hoikille komponenteille. ↩
-
Tarkastele virtausnopeuden määritelmää ja sen merkitystä nopeuden laskemisessa nestejärjestelmissä. ↩



