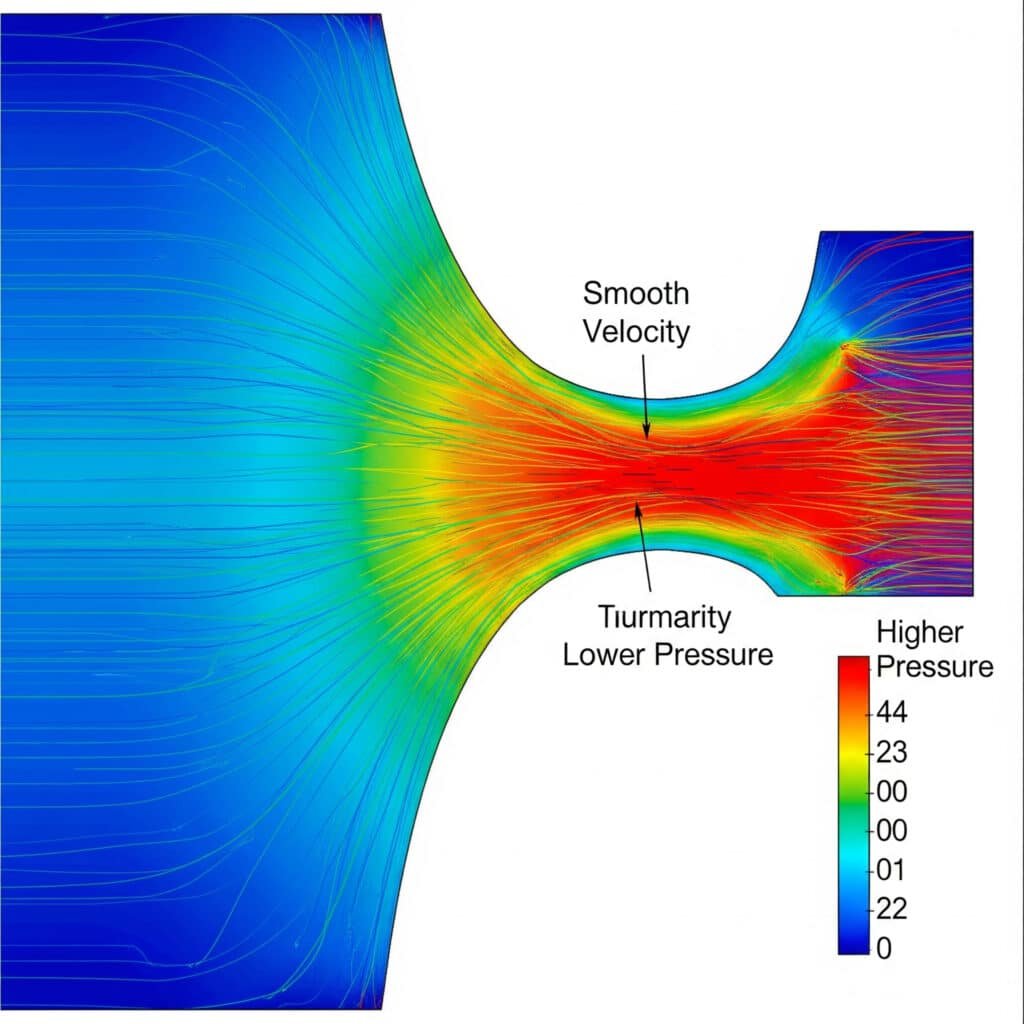
Kaasun virtausongelmat aiheuttavat valmistajille vuosittain miljardien eurojen kustannukset energiahukan ja järjestelmävikojen vuoksi. Insinöörit soveltavat usein nestevirtausperiaatteita kaasujärjestelmiin, mikä johtaa katastrofaalisiin virhearviointeihin. Kaasuvirtausperiaatteiden ymmärtäminen ehkäisee kalliita suunnitteluvirheitä ja turvallisuusriskejä.
Kaasun virtausperiaatetta säätelevät jatkuvuusyhtälö, impulssin säilyminen ja energian säilyminen, jossa kaasun nopeus, paine, tiheys ja lämpötila vaikuttavat toisiinsa seuraavien tekijöiden kautta kokoonpuristuva virtaus1 yhtälöt eroavat olennaisesti kokoonpuristumattomasta nestevirtauksesta.
Kaksi vuotta sitten työskentelin brittiläisen Sarah Thompson -nimisen kemianinsinöörin kanssa, jonka maakaasun jakelujärjestelmässä esiintyi vaarallisia painevaihteluita. Hänen tiiminsä käytti kokoonpuristumattomia virtauslaskelmia kokoonpuristuvalle kaasuvirtaukselle. Kun otimme käyttöön oikeat kaasun virtausperiaatteet, poistimme paineiskut ja vähensimme energiankulutusta 35%.
Sisällysluettelo
- Mitkä ovat kaasun virtauksen perusperiaatteet?
- Miten kokoonpuristuvan virtauksen yhtälöt eroavat nestevirtauksesta?
- Mitkä tekijät vaikuttavat kaasun virtauskäyttäytymiseen teollisuusjärjestelmissä?
- Miten paine, lämpötila ja nopeus vaikuttavat toisiinsa kaasuvirtauksessa?
- Mitkä ovat erityyppiset kaasun virtausjärjestelmät?
- Kuinka laskea ja optimoida kaasuvirtaus teollisissa sovelluksissa?
- Päätelmä
- Usein kysytyt kysymykset kaasun virtauksen periaatteista
Mitkä ovat kaasun virtauksen perusperiaatteet?
Kaasuvirtaus toimii kolmen perustavanlaatuisen säilymislain mukaisesti, jotka säätelevät kaikkea nesteen liikettä, mutta joilla on ainutlaatuisia ominaisuuksia kaasun kokoonpuristuvuuden ja tiheyden vaihtelun vuoksi.
Kaasun virtausperiaatteet perustuvat massan säilymiseen (jatkuvuusyhtälö), impulssin säilymiseen (Newtonin toinen laki) ja energian säilymiseen (termodynamiikan ensimmäinen laki), joita on muutettu kokoonpuristuvan nesteen käyttäytymistä varten.
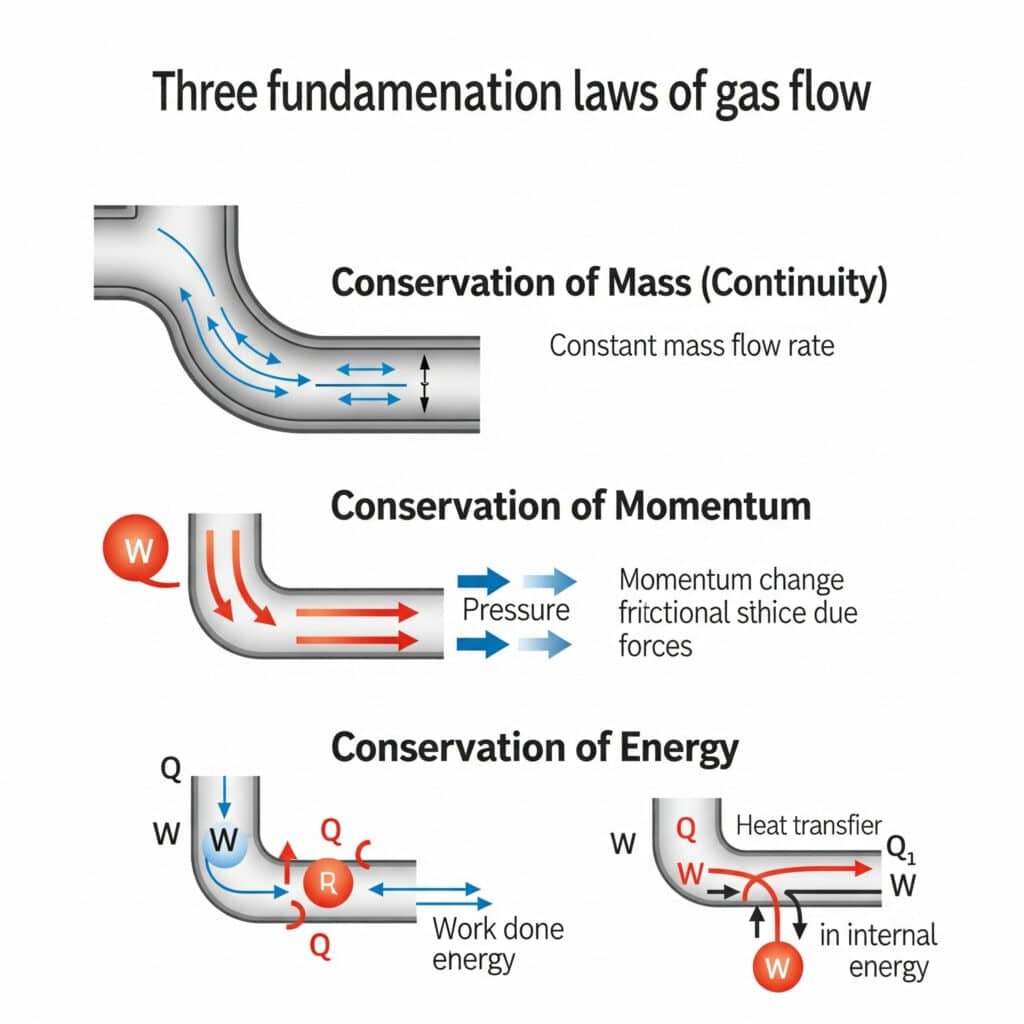
Massan säilyminen (jatkuvuusyhtälö)
Kaasuvirtauksen jatkuvuusyhtälössä otetaan huomioon paineen ja lämpötilan vaihtelun aiheuttamat tiheyden muutokset, toisin kuin kokoonpuristumattomissa nesteissä.
Kaasuvirtauksen jatkuvuusyhtälö:
∂ρ/∂t + ∇-(ρV) = 0
Tasaista virtausta varten: ρ₁A₁V₁ = ρ₂A₂V₂.
Missä:
- ρ = Kaasun tiheys (vaihtelee paineen ja lämpötilan mukaan)
- A = poikkipinta-ala
- V = Kaasun nopeus
- t = aika
Keskeiset seuraukset:
- Kaasun tiheys muuttuu paineen ja lämpötilan mukaan
- Massavirta pysyy vakiona tasaisessa virtauksessa
- Nopeus kasvaa tiheyden pienentyessä
- Alueen muutokset vaikuttavat sekä nopeuteen että tiheyteen
Momentin säilyminen
Kaasuvirtauksen momentin säilymisessä otetaan huomioon kokoonpuristuvaan nesteeseen vaikuttavat painevoimat, viskoosivoimat ja kehon voimat.
Momenttiyhtälö (Navier-Stokes2):
ρ(∂V/∂t + V-∇V) = -∇p + μ∇²V + ρg
Kaasuvirtasovelluksia varten:
- Painegradienttitermi hallitsee nopeassa virtauksessa.
- Viskoosivaikutukset ovat tärkeitä seinämien lähellä ja laminaarivirtauksessa.
- Kokoonpuristuvuusvaikutukset tulevat merkittäviksi yli Mach 0,3 -lentokorkeuden
Energian säilyminen
Kaasuvirtauksen energian säilyminen sisältää liike-energian, potentiaalienergian, sisäisen energian ja virtaustyön, ja siinä otetaan huomioon puristumisesta ja paisumisesta johtuvat lämpötilan muutokset.
Energiayhtälö:
h + V²/2 + gz = vakio (virtaviivaa pitkin)
Missä:
- h = Ominaisentalpia (sisältää sisäisen energian ja virtaustehon).
- V²/2 = Kineettinen energia massayksikköä kohti
- gz = potentiaalienergia massayksikköä kohti
Energianäkökohdat:
| Energiamuoto | Kaasun virtauksen vaikutus | Tyypillinen suuruusluokka |
|---|---|---|
| Kineettinen energia | Merkittävä suurilla nopeuksilla | V²/2 |
| Paine-energia | Hallitseva useimmissa sovelluksissa | p/ρ |
| Sisäinen energia | Muutokset lämpötilan mukaan | CᵥT |
| Virtaustyö | Tarvitaan kaasun liikettä varten | pv |
Valtion yhtälö
Kaasun virtaus edellyttää paine-, tiheys- ja lämpötilayhtälöä, joka useimmissa teollisuussovelluksissa on tyypillisesti ideaalikaasulaki.
Ideaalikaasun laki:
p = ρRT
Missä:
- p = Absoluuttinen paine
- ρ = Kaasun tiheys
- R = Ominaiskaasuvakio
- T = Absoluuttinen lämpötila
Todellisissa kaasuissa saatetaan tarvita monimutkaisempia tilanyhtälöitä, kuten van der Waalsin tai Redlich-Kwongin yhtälöitä.
Miten kokoonpuristuvan virtauksen yhtälöt eroavat nestevirtauksesta?
Tiivistyvä kaasuvirtaus käyttäytyy olennaisesti eri tavalla kuin kokoonpuristumaton nestevirtaus, mikä edellyttää erityisiä analyysimenetelmiä ja suunnittelua koskevia näkökohtia.
Tiivistyvä virtaus eroaa kokoonpuristuvasta virtauksesta tiheysvaihteluiden, äänennopeusrajoitusten, paineaaltojen muodostumisen ja lämpötilan ja paineen kytkeytymisen vuoksi, joita ei esiinny kokoonpuristumattomissa nestevirtausjärjestelmissä.
Tiheyden vaihtelun vaikutukset
Kaasun tiheys muuttuu merkittävästi paineen ja lämpötilan mukaan, mikä vaikuttaa virtausmalleihin, nopeusjakaumiin ja järjestelmän suunnitteluvaatimuksiin.
Tiheyden muutoksen vaikutukset:
- Nopeus Kiihtyvyys: Kaasu kiihtyy laajentuessaan
- Painehäviö: Epälineaariset paine-virtaussuhteet
- Lämpötilan vaikutukset: Tiheys kääntäen verrannollinen lämpötilaan
- Tukahdutettu virtaus: Virtausnopeuden enimmäisrajoitukset
Äänen nopeus ja Machin luku
Kaasun virtauskäyttäytyminen muuttuu dramaattisesti, kun nopeus lähestyy äänen nopeutta, mikä aiheuttaa kriittisiä suunnittelurajoituksia, joita ei ole nestemäisissä järjestelmissä.
Äänen nopeuden laskeminen:
a = √(γRT)
Missä:
- a = äänen nopeus kaasussa
- γ = Ominaislämpösuhde (Cp/Cv)
- R = Ominaiskaasuvakio
- T = Absoluuttinen lämpötila
Machin luku3 Merkitys:
M = V/a (Nopeuden suhde äänen nopeuteen)
| Mach-alue | Virtausjärjestelmä | Ominaisuudet |
|---|---|---|
| M < 0.3 | Yhteensopimaton | Tiheys olennaisesti vakio |
| 0.3 < M < 1.0 | Aliääninen Puristuva | Merkittävät tiheyden muutokset |
| M = 1.0 | Sonic | Kriittiset virtausolosuhteet |
| M > 1.0 | Supersonic | Iskuaallot mahdollisia |
Tukahdutetun virtauksen ilmiö
Kuristunut virtaus4 tapahtuu, kun kaasun nopeus saavuttaa sonic-olosuhteet, mikä rajoittaa maksimivirtausnopeutta riippumatta virtaussuunnan jälkeisestä paineenalennuksesta.
Tukkeutuneet virtausolosuhteet:
- Suurin saavutettu massavirta
- Alavirran paineen muutokset eivät vaikuta ylävirtaan.
- Kriittinen painesuhde: p₂/p₁ ≈ 0,53 ilmalle.
- Yleinen suuttimissa, suuaukoissa ja säätöventtiileissä.
Lämpötila-paine kytkentä
Kaasuvirtaukseen liittyy merkittäviä lämpötilan muutoksia paisumisen ja puristamisen vuoksi, mikä vaikuttaa järjestelmän suorituskykyyn ja suunnitteluun.
Termodynaamiset prosessit:
- Isentrooppinen virtaus: Palautuva, adiabaattinen prosessi
- Isoterminen virtaus: Vakiolämpötila (hidas virtaus ja lämmönsiirto).
- Adiabaattinen virtaus: Ei lämmönsiirtoa (nopea virtaus)
- Polytrooppinen virtaus: Yleinen tapaus lämmönsiirron kanssa
Mitkä tekijät vaikuttavat kaasun virtauskäyttäytymiseen teollisuusjärjestelmissä?
Useat tekijät vaikuttavat kaasun virtauskäyttäytymiseen teollisissa sovelluksissa, mikä edellyttää kattavaa analyysia järjestelmän asianmukaista suunnittelua ja toimintaa varten.
Keskeisiä tekijöitä ovat kaasun ominaisuudet, järjestelmän geometria, käyttöolosuhteet, lämmönsiirtovaikutukset ja seinäkekitka, jotka yhdessä määrittävät virtaustavat, painehäviöt ja järjestelmän suorituskyvyn.
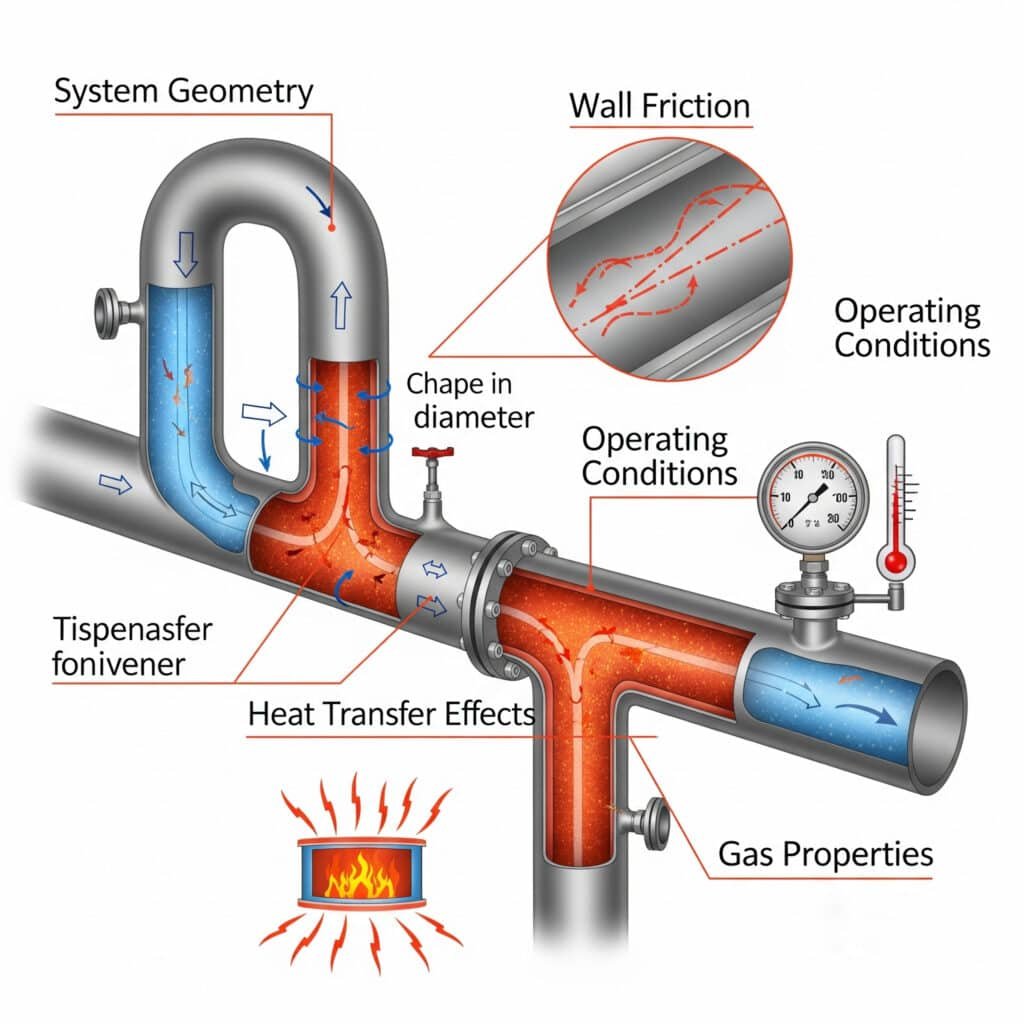
Kaasun ominaisuudet Vaikutus
Eri kaasujen virtausominaisuudet vaihtelevat niiden molekyyliominaisuuksien, ominaislämpösuhteiden ja termodynaamisen käyttäytymisen perusteella.
Kriittiset kaasun ominaisuudet:
| Kiinteistö | Symboli | Vaikutus virtaukseen | Tyypilliset arvot |
|---|---|---|---|
| Ominaislämpösuhde | γ | Äänen nopeus, laajeneminen | 1.4 (ilma), 1.3 (CO₂) |
| Kaasuvakio | R | Tiheyden ja paineen suhde | 287 J/kg-K (ilma) |
| Viskositeetti | μ | Kitkahäviöt | 1,8×10-⁵ Pa-s (ilma) |
| Molekyylipaino | M | Tiheys tietyissä olosuhteissa | 29 kg/kmol (ilma) |
Järjestelmän geometrian vaikutukset
Putkien halkaisija, pituus, liitososat ja virtauspinta-alan muutokset vaikuttavat merkittävästi kaasun virtaustapaan ja painehäviöihin.
Geometriaa koskevat näkökohdat:
- Putken halkaisija: Vaikuttaa nopeuteen ja kitkahäviöihin.
- Pituus: Määrittää kitkan kokonaispainehäviön
- Alueen muutokset: Luo kiihdytys-/ hidastustehosteita
- Varusteet: Aiheuttavat paikallisia painehäviöitä
- Pinnan karheus: Vaikuttaa kitkakerroin
Käyttöpaine ja -lämpötila
Järjestelmän käyttöolosuhteet vaikuttavat suoraan kaasun tiheyteen, viskositeettiin ja virtauskäyttäytymiseen termodynaamisten suhteiden kautta.
Käyttöolosuhteiden vaikutukset:
- Korkea paine: Lisää tiheyttä, vähentää kokoonpuristuvuusvaikutuksia
- Alhainen paine: Pienentää tiheyttä, lisää nopeutta
- Korkea lämpötila: Vähentää tiheyttä, lisää äänen nopeutta.
- Matala lämpötila: Lisää tiheyttä, voi aiheuttaa tiivistymistä
Lämmönsiirron vaikutukset
Lämmön lisääminen tai poistaminen kaasun virtauksen aikana vaikuttaa merkittävästi lämpötilan, tiheyden ja paineen jakautumiseen.
Lämmönsiirtoskenaariot:
- Lämmitys: Nostaa lämpötilaa, vähentää tiheyttä, kiihdyttää virtausta.
- Jäähdytys: Alentaa lämpötilaa, lisää tiheyttä, hidastaa virtausta.
- Adiabaattinen: Ei lämmönsiirtoa, lämpötila muuttuu laajenemisen/puristumisen vuoksi.
- Isoterminen: Lämmönsiirron avulla ylläpidetty vakiolämpötila
Seinän kitkavaikutus
Kaasun ja putken seinämien välinen kitka aiheuttaa painehäviöitä ja vaikuttaa nopeusprofiileihin, mikä on erityisen tärkeää pitkissä putkistoissa.
Kitkahäviön laskeminen:
Δp = f × (L/D) × (ρV²/2)
Missä:
- f = kitkakerroin (Reynoldsin luvun ja karheuden funktio).
- L = Putken pituus
- D = Putken halkaisija
- ρ = Kaasun tiheys
- V = Kaasun nopeus
Miten paine, lämpötila ja nopeus vaikuttavat toisiinsa kaasuvirtauksessa?
Paineen, lämpötilan ja nopeuden välinen vuorovaikutus kaasuvirtauksessa luo monimutkaisia suhteita, jotka on ymmärrettävä, jotta järjestelmä voidaan suunnitella ja analysoida oikein.
Kaasuvirtauksen vuorovaikutukset noudattavat termodynaamisia suhteita, joissa paineen muutokset vaikuttavat lämpötilaan ja tiheyteen, nopeuden muutokset vaikuttavat paineeseen impulssivaikutusten kautta ja lämpötilan muutokset vaikuttavat kaikkiin muihin ominaisuuksiin tilayhtälön kautta.
Paine-nopeussuhteet
Kaasun nopeus ja paine ovat käänteisessä suhteessa toisiinsa Bernoullin yhtälön avulla, joka on muunnettu kokoonpuristuvaa virtausta varten, mikä luo ainutlaatuisia suunnitteluhaasteita.
Kaasuvirtauksen muunnettu Bernoullin yhtälö:
∫dp/ρ + V²/2 + gz = vakio
Ideaalikaasulle: γ/(γ-1) × (p/ρ) + V²/2 = vakio.
Paine-nopeusvaikutukset:
- Painehäviö: Aiheuttaa nopeuden kasvun kaasun laajenemisen vuoksi
- Nopeuden kasvu: Voi aiheuttaa ylimääräistä painehäviötä momenttivaikutusten vuoksi
- Kiihtyvyys: Esiintyy luonnostaan kaasun laajetessa järjestelmässä
- Hidastus: Vaatii paineen nostoa tai alueen laajentamista
Lämpötila-nopeuskytkentä
Kaasun lämpötila ja nopeus kytkeytyvät toisiinsa energian säilymisen kautta, ja lämpötilan muutokset vaikuttavat kaasun ominaisuuksiin ja virtauskäyttäytymiseen.
Lämpötila-nopeussuhteet:
T₀ = T + V²/(2Cp)
Missä:
- T₀ = pysähtymislämpötila (kokonaislämpötila).
- T = Staattinen lämpötila
- V = Kaasun nopeus
- Cp = ominaislämpö vakiopaineessa
Käytännön vaikutukset:
- Suuren nopeuden kaasuvirtaus alentaa staattista lämpötilaa.
- Pysähtymislämpötila pysyy vakiona adiabaattisessa virtauksessa.
- Lämpötilan muutokset vaikuttavat kaasun tiheyteen ja viskositeettiin.
- Jäähdytys voi aiheuttaa kondensaatiota joissakin kaasuissa.
Paineen ja lämpötilan vaikutukset
Paine ja lämpötila vaikuttavat toisiinsa tilanyhtälön ja termodynaamisten prosessien kautta, mikä vaikuttaa kaasun tiheyteen ja virtausominaisuuksiin.
Termodynaamiset prosessisuhteet:
| Prosessin tyyppi | Paineen ja lämpötilan suhde | Hakemus |
|---|---|---|
| Isentrooppinen | p/p₀ = (T/T₀)^(γ/(γ-1)) | Suuttimet, hajottimet |
| Isoterminen | pV = vakio, T = vakio | Hidas virtaus lämmönsiirrolla |
| Isobaarinen | p = vakio | Vakiopaineinen lämmitys |
| Isokorinen | V = vakio | Vakiotilavuuslämmitys |
Tiheyden vaihtelut
Kaasun tiheys vaihtelee sekä paineen että lämpötilan mukaan ideaalikaasulain mukaisesti, mikä aiheuttaa monimutkaisen virtauskäyttäytymisen.
Tiheyden laskeminen:
ρ = p/(RT)
Tiheyden vaikutus virtaukseen:
- Korkea tiheys: Pienempi nopeus tietyllä massavirtauksella
- Matala tiheys: Suurempi nopeus, mahdolliset kokoonpuristuvuusvaikutukset
- Tiheysasteet: Luo kelluvuus- ja sekoitustehosteita
- Tiheyden muutokset: Vaikuttaa momentin ja energian siirtoon
Autoin hiljattain yhdysvaltalaista maakaasualan insinööriä Robert Cheniä Teksasissa optimoimaan putkistojärjestelmänsä. Ottamalla asianmukaisesti huomioon lämpötilan, paineen ja nopeuden vuorovaikutukset vähensimme pumppausenergiaa 28% ja lisäsimme läpivirtauskapasiteettia 15%.
Mitkä ovat erityyppiset kaasun virtausjärjestelmät?
Kaasuvirtauksessa on erilaisia nopeuteen, paineolosuhteisiin ja järjestelmän geometriaan perustuvia järjestelmiä, jotka kaikki vaativat erityisiä analyysimenetelmiä ja suunnittelua koskevia näkökohtia.
Kaasuvirtausjärjestelmiin kuuluvat laminaarinen, turbulenttinen, aliääni-, ääni- ja yliäänivirtaus, joille kullekin on ominaista erilaiset nopeusprofiilit, painesuhteet ja lämmönsiirto-ominaisuudet.
Laminaarinen vs. turbulenttinen virtaus
Kaasuvirtauksen siirtyminen laminaarisesta turbulenttiin perustuu seuraaviin tekijöihin Reynoldsin luku5, jotka vaikuttavat painehäviöihin, lämmönsiirtoon ja sekoitusominaisuuksiin.
Reynoldsin luku kaasuvirtauksessa:
Re = ρVD/μ
Missä:
- ρ = Kaasun tiheys (vaihtelee paineen ja lämpötilan mukaan)
- V = Keskimääräinen nopeus
- D = Putken halkaisija
- μ = dynaaminen viskositeetti
Virtausalueluokitukset:
| Reynoldsin luku | Virtausjärjestelmä | Ominaisuudet |
|---|---|---|
| Re < 2300 | Laminaari | Tasainen, ennustettava virtaus |
| 2300 < Re < 4000 | Siirtymä | Epävakaa, sekakäyttäytyminen |
| Re > 4000 | Turbulentti | Kaaoottinen, tehostettu sekoittuminen |
Subsonic Flow Regime
Aliäänivirtausta esiintyy, kun kaasun nopeus on pienempi kuin paikallinen äänen nopeus, jolloin painehäiriöt voivat levitä virtaussuuntaan.
Aliäänivirtauksen ominaisuudet:
- Machin luku: M < 1.0
- Paineen leviäminen: Häiriöt kulkeutuvat ylävirtaan
- Virtauksen säätö: Alavirran olosuhteet vaikuttavat koko järjestelmään
- Tiheyden muutokset: Kohtalainen, ennakoitavissa olevat vaihtelut
- Suunnittelun joustavuus: Useat ratkaisut mahdollisia
Subsonic Flow -sovellukset:
- Useimmat teollisuuden kaasunjakelujärjestelmät
- LVAC- ja ilmanvaihtojärjestelmät
- Matalapaineiset pneumaattiset järjestelmät
- Kemialliset prosessilaitteet
- Voimalaitoskaasun käsittely
Sonic Flow (tukahdutettu virtaus)
Äänivirtaus syntyy, kun kaasun nopeus on yhtä suuri kuin paikallinen äänen nopeus, mikä luo kriittiset virtausolosuhteet, joilla on ainutlaatuiset ominaisuudet.
Sonic Flow -ominaisuudet:
- Machin luku: M = 1,0 täsmälleen
- Suurin massavirta: Ei voida ylittää
- Paine Riippumattomuus: Alavirran paine ei vaikuta virtaukseen
- Kriittinen painesuhde: Tyypillisesti noin 0,53 ilmassa
- Lämpötilan vaikutukset: Merkittävä lämpötilan lasku
Sonic Flow -sovellukset:
- Kaasuturbiinien suuttimet
- Varoventtiilit
- Virtauksen mittauslaitteet
- Rakettimoottorin suuttimet
- Korkeapainekaasun säätimet
Yliäänivirtaus
Yliäänivirtaus tapahtuu, kun kaasun nopeus ylittää äänen nopeuden, jolloin syntyy paineaaltoja ja ainutlaatuisia virtausilmiöitä.
Yliäänivirtauksen ominaisuudet:
- Machin luku: M > 1.0
- Iskuaallot: Äkilliset paineen ja lämpötilan muutokset
- Virtaussuunta: Tieto ei voi kulkea ylävirtaan
- Laajenemisaallot: Tasaiset paineenalennukset
- Suunnittelun monimutkaisuus: Vaatii erikoisanalyysin
Iskuaaltotyypit:
| Iskun tyyppi | Ominaisuudet | Sovellukset |
|---|---|---|
| Normaali sokki | Kohtisuorassa virtaukseen nähden | Hajottimet, tuloaukot |
| Viisto isku | Kulmattu virtaussuuntaan nähden | Yliäänilentokoneet |
| Laajennustuuletin | Asteittainen paineen alentaminen | Suuttimen rakenne |
Hypersoninen virtaus
Hypersoninen virtaus tapahtuu hyvin suurilla Machin luvuilla (tyypillisesti M > 5), jolloin lisävaikutukset tulevat tärkeiksi.
Hypersoniset vaikutukset:
- Todelliset kaasuvaikutukset: Ideaalikaasun laki hajoaa
- Kemialliset reaktiot: Dissosiaatio ja ionisaatio
- Lämmönsiirto: Äärimmäiset lämmitysvaikutukset
- Viskoosiset vaikutukset: Rajakerroksen vuorovaikutukset
Kuinka laskea ja optimoida kaasuvirtaus teollisissa sovelluksissa?
Kaasuvirtauslaskelmat edellyttävät erityisiä menetelmiä, joissa otetaan huomioon kokoonpuristuvuusvaikutukset, kun taas optimoinnissa keskitytään energiankulutuksen minimointiin ja järjestelmän suorituskyvyn maksimointiin.
Kaasuvirtauslaskelmissa käytetään kokoonpuristuvia virtausyhtälöitä, kitkakertoimien korrelaatioita ja termodynaamisia suhteita, kun taas optimointi käsittää putkien mitoituksen, painetason valinnan ja järjestelmän kokoonpanon energiakustannusten minimoimiseksi.
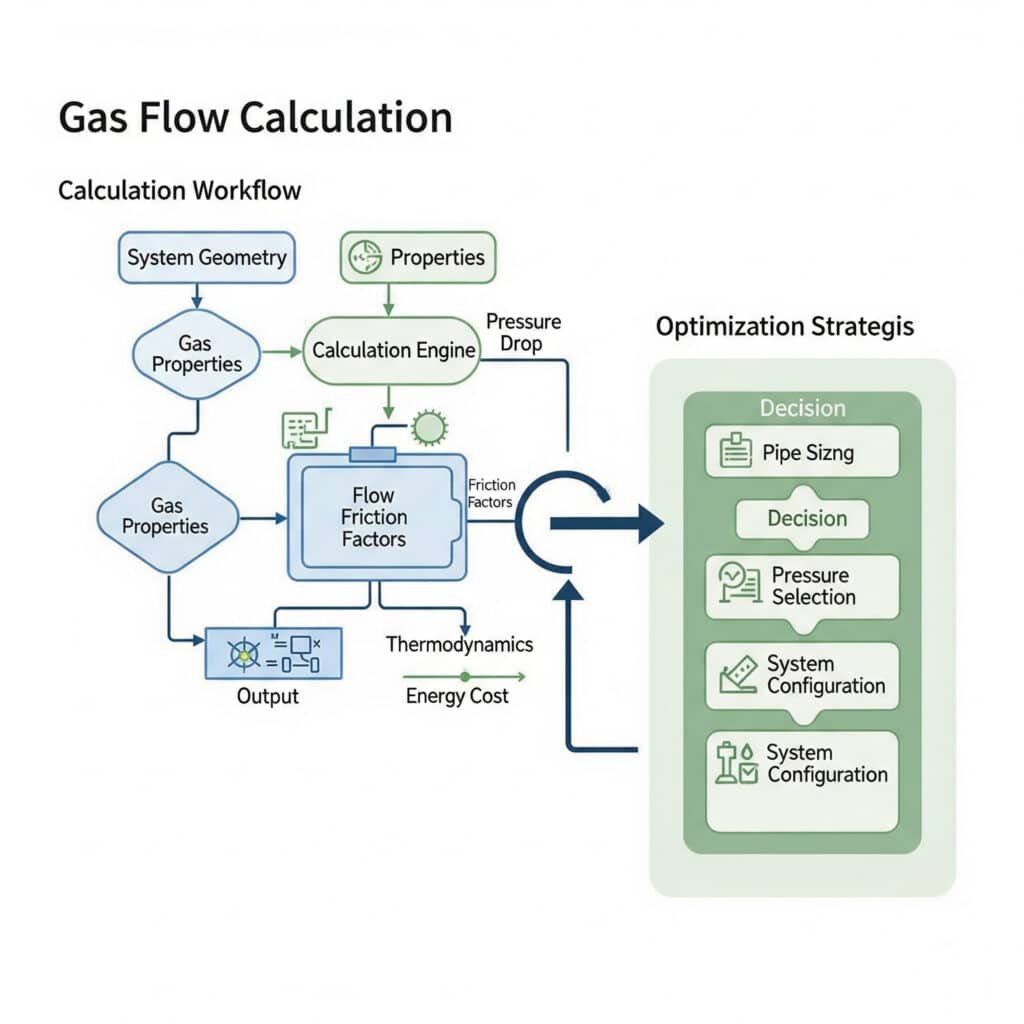
Kaasuvirran peruslaskelmat
Kaasuvirtauslaskelmat aloitetaan perusyhtälöistä, joita on muutettu kokoonpuristuvan virtauksen vaikutusten ja todellisten kaasun ominaisuuksien mukaan.
Massavirtauksen laskeminen:
ṁ = ρAV = (p/RT)AV
Aukon läpi kulkevan kuristetun virtauksen osalta:
ṁ = CdA√(γρp)[2/(γ+1)]^((γ+1)/(2(γ-1)))
Missä:
- Cd = purkautumiskerroin
- A = aukon pinta-ala
- γ = Ominaislämpösuhde
- ρ = virtaussuunnan tiheys
- p = virtaussuuntaan vaikuttava paine
Painehäviölaskelmat
Kaasuvirtauksen painehäviölaskelmissa on kitkahäviöiden lisäksi otettava huomioon kaasun laajenemisesta johtuvat kiihtyvyysvaikutukset.
Painehäviön kokonaiskomponentit:
- Kitkan painehäviö: Seinän leikkausjännityksen vuoksi
- Kiihtyvyys Painehäviö: Nopeuden kasvun vuoksi
- Korkeus Painehäviö: Gravitaatiovaikutusten vuoksi
- Sovituksen painehäviö: Virtaushäiriöiden vuoksi
Kitkapainehäviön kaava:
Δpf = f(L/D)(ρV²/2)
Kiihtyvyyspainehäviö:
Δpa = ρ₂V₂² - ρ₁V₁². (aluemuutoksia varten)
Putkiston virtausanalyysi
Pitkien putkistojen analysointi edellyttää iteratiivisia laskelmia, koska kaasun ominaisuudet muuttuvat putkiston pituudella.
Putkilinjan laskentavaiheet:
- Jaa putkisto: Segmentteihin, joilla on vakio-ominaisuudet
- Segmentin ominaisuuksien laskeminen: Paine, lämpötila, tiheys
- Virtausjärjestelmän määrittäminen: Laminaarinen tai turbulenttinen
- Painehäviön laskeminen: Kunkin segmentin osalta
- Päivitä ominaisuudet: Seuraavaa segmenttiä varten
- Iteroi: Kunnes saavutetaan konvergenssi
Yksinkertaistettu putkiston yhtälö:
p₁² - p₂² = (fLṁ²RT)/(A²Dρ₀).
Missä:
- p₁, p₂ = tulo- ja lähtöpaineet.
- f = Keskimääräinen kitkakerroin
- L = Putkilinjan pituus
- ṁ = Massavirta
- R = kaasuvakio
- T = Keskilämpötila
- A = Putken pinta-ala
- D = Putken halkaisija
- ρ₀ = Vertailutiheys
Järjestelmän optimointistrategiat
Kaasuvirtausjärjestelmän optimoinnissa tasapainotetaan pääomakustannukset, käyttökustannukset ja suorituskykyvaatimukset, jotta elinkaarikustannukset olisivat mahdollisimman pienet.
Optimointiparametrit:
| Parametri | Vaikutus järjestelmään | Optimointistrategia |
|---|---|---|
| Putken halkaisija | Pääomakustannukset vs. painehäviö | Taloudellisen halkaisijan laskeminen |
| Käyttöpaine | Puristuskustannukset vs. putkikustannukset | Painetason optimointi |
| Kompressorin porrastus | Tehokkuus vs. monimutkaisuus | Vaiheen numeron optimointi |
| Lämmönvaihtimen koko | Lämmön talteenotto vs. pääomakustannukset | Taloudellinen lämmönvaihto |
Taloudellinen putkien mitoitus
Taloudellisessa putkiston mitoituksessa tasapainotetaan putkiston pääomakustannuksia ja pumppausenergiakustannuksia järjestelmän käyttöiän aikana.
Taloudellisen halkaisijan kaava:
D_economic = K(ṁ/ρ)^0,37
Jos K riippuu:
- Energiakustannukset
- Putkikustannukset
- Järjestelmän käyttöikä
- Korko
- Käyttötunnit vuodessa
Virtauksen mittaus ja säätö
Tarkka kaasuvirtauksen mittaus ja säätö edellyttävät ymmärrystä kokoonpuristuvan virtauksen vaikutuksista mittauslaitteisiin.
Virtausmittaukseen liittyviä näkökohtia:
- Suuaukkolevyt: Vaaditaan kokoonpuristuvuuskorjauksia
- Venturi-mittarit: Vähemmän herkkä kokoonpuristuvuudelle
- Turbiinimittarit: Kaasun tiheyden muutokset vaikuttavat
- Ultraäänimittarit: Vaatii lämpötilan kompensoinnin
- Coriolis-mittarit: Suora massavirran mittaus
Laskennallinen virtausdynamiikka (CFD)
Monimutkaiset kaasuvirtausjärjestelmät hyötyvät CFD-analyysistä suorituskyvyn optimoimiseksi ja käyttäytymisen ennustamiseksi eri käyttöolosuhteissa.
CFD-sovellukset:
- Monimutkaiset geometriat: Epäsäännölliset muodot ja varusteet
- Lämmönsiirto: Yhdistetty virtaus ja lämpöanalyysi
- Sekoitusanalyysi: Kaasun koostumuksen vaihtelut
- Optimointi: Suunnitteluparametritutkimukset
- Vianmääritys: Virtausongelmien tunnistaminen
Työskentelin hiljattain Albertassa kanadalaisen petrokemian insinöörin David Wilsonin kanssa, jonka kaasunkäsittelylaitoksessa oli tehokkuusongelmia. Käyttämällä CFD-analyysiä yhdistettynä asianmukaisiin kaasuvirtalaskelmiin tunnistimme kierrätysvyöhykkeet, jotka aiheuttivat 20%:n energiahukkaa. Suunnittelumuutosten toteuttamisen jälkeen energiankulutus väheni 18% ja prosessointikapasiteetti kasvoi.
Päätelmä
Kaasuvirtausperiaatteet ohjaavat kokoonpuristuvan nesteen käyttäytymistä tiheyden vaihteluiden mukaan muunnettujen säilymislakien avulla, mikä edellyttää erityisiä analyysimenetelmiä, joissa otetaan huomioon paineen ja lämpötilan sekä nopeuden vuorovaikutukset ja kokoonpuristuvuusvaikutukset, jotka eroavat olennaisesti nestevirtausjärjestelmistä.
Usein kysytyt kysymykset kaasun virtauksen periaatteista
Mikä on kaasun virtauksen perusperiaate?
Kaasuvirtaus toimii massan, impulssin ja energian säilymisen perusteella, ja sitä muutetaan kokoonpuristuvan nesteen käyttäytymistä varten, jolloin kaasun tiheys vaihtelee paineen ja lämpötilan mukaan, jolloin syntyy nopeus-paine-lämpötila-vuorovaikutuksia.
Miten kaasuvirtaus eroaa nestevirtauksesta?
Kaasuvirtaukseen liittyy merkittäviä tiheyden muutoksia, äänennopeusrajoituksia, lämpötilan ja paineen kytkeytymistä ja tukkeutumisilmiöitä, joita ei esiinny kokoonpuristumattomissa nestevirtausjärjestelmissä.
Mitä on kuristettu virtaus kaasujärjestelmissä?
Kuristunut virtaus syntyy, kun kaasun nopeus saavuttaa sonic-olosuhteet (Mach = 1,0), jolloin suurin massavirta rajoittuu riippumatta virtaussuunnan jälkeisestä paineenalennuksesta, mikä esiintyy yleisesti suuttimissa ja säätöventtiileissä.
Miten lasketaan kaasun virtausnopeus?
Kaasun virtausnopeuden laskennassa käytetään yhtälöä ṁ = ρAV, jossa tiheys vaihtelee paineen ja lämpötilan mukaan ideaalikaasulain mukaisesti, mikä edellyttää iteratiivisia ratkaisuja monimutkaisissa järjestelmissä.
Mitkä tekijät vaikuttavat kaasun virtauskäyttäytymiseen?
Keskeisiä tekijöitä ovat kaasun ominaisuudet (molekyylipaino, ominaislämpösuhde), järjestelmän geometria (putken halkaisija, liitokset), käyttöolosuhteet (paine, lämpötila) ja lämmönsiirtovaikutukset.
Miksi Machin luku on tärkeä kaasun virtauksessa?
Machin luku (nopeus/äänen nopeus) määrittää virtausjärjestelmän ominaisuudet: aliäänivirtaus (M1) synnyttää paineaaltoja.
-
Selittää perustavanlaatuisen eron kokoonpuristuvan virtauksen, jossa nesteen tiheys muuttuu merkittävästi paineen mukaan, ja kokoonpuristumattoman virtauksen, jossa tiheys oletetaan vakioksi, välillä, mikä on keskeinen ero kaasu- ja nestedynamiikan välillä. ↩
-
Tarjoaa yleiskatsauksen Navier-Stokesin yhtälöihin, jotka ovat nestemekaniikan perusta ja kuvaavat viskoosien nestemäisten aineiden liikettä momentin säilymisen perusteella. ↩
-
Tarjoaa yksityiskohtaisen määritelmän Machin luvusta, joka on nestedynamiikan dimensioton suure, joka kuvaa rajan ohi kulkevan virtausnopeuden suhdetta paikalliseen äänen nopeuteen ja jota käytetään virtausjärjestelmien luokitteluun. ↩
-
Kuvaa ilmiötä, jossa virtausta tukahdutetaan, mikä on kokoonpuristuvan virtauksen rajoittava tila, jossa massavirta ei enää kasva, kun virtaussuunnan jälkeinen paine laskee, koska nopeus kapeimmassa kohdassa on saavuttanut äänen nopeuden. ↩
-
Selittää Reynoldsin luvun, joka on keskeinen dimensioton suure nestemekaniikassa, jota käytetään virtaustapojen ennustamiseen ja joka auttaa erottamaan laminaarisen (tasaisen) ja turbulentin (kaoottisen) virtausjärjestelmän toisistaan. ↩


