
Onko sinulla vaikeuksia ennustaa pneumaattisen sylinterisi todellista suorituskykyä? Monet insinöörit laskevat voimantuoton ja painevaatimukset väärin, mikä johtaa järjestelmävirheisiin ja kalliisiin seisokkiaikoihin. On kuitenkin olemassa yksinkertainen tapa hallita nämä laskelmat.
Pneumaattiset sylinterit toimivat fysiikan perusperiaatteiden mukaisesti, ensisijaisesti seuraavin tavoin Pascalin laki1, jonka mukaan rajoitettuun nesteeseen kohdistuva paine välittyy yhtä paljon kaikkiin suuntiin. Tämän ansiosta sylinterivoima voidaan laskea kertomalla paine männän tehollisella pinta-alalla, ja virtausnopeudet ja paineyksiköt edellyttävät tarkkoja muunnoksia järjestelmän tarkkaa suunnittelua varten.
Olen yli kymmenen vuotta auttanut asiakkaita optimoimaan pneumatiikkajärjestelmiään ja nähnyt, miten näiden perusperiaatteiden ymmärtäminen voi muuttaa järjestelmän luotettavuutta. Anna minun jakaa käytännön tietoa, joka auttaa sinua välttämään yleiset virheet, joita näen päivittäin.
Sisällysluettelo
- Miten Pascalin laki määrittää sylinterin voimantuoton?
- Mikä on ilmavirran ja sylinterien paineen suhde?
- Miksi paineyksikön muuntamisen ymmärtäminen on tärkeää järjestelmän suunnittelussa?
- Päätelmä
- Pneumaattisten järjestelmien fysiikkaa koskevat usein kysytyt kysymykset
Miten Pascalin laki määrittää sylinterin voimantuoton?
Pascalin lain ymmärtäminen on olennaisen tärkeää sylinterien suorituskyvyn ennustamisessa ja optimoinnissa kaikissa paineilmajärjestelmissä.
Pascalin lain mukaan suljetun järjestelmän nesteeseen kohdistuva paine siirtyy tasaisesti koko nesteeseen. Pneumaattisten sylintereiden osalta tämä tarkoittaa, että tuotettu voima on yhtä suuri kuin paine kerrottuna männän tehollisella pinta-alalla (F = P × A). Tämä yksinkertainen suhde on kaikkien sylinterivoiman laskelmien perusta.

Voiman laskennan johdanto
Tarkastellaan sylinterivoiman laskennan matemaattista johtamista:
Voiman perusyhtälö
Sylinterivoiman perusyhtälö on:
F = P × A
Missä:
- F = voimantuotto (N)
- P = Paine (Pa)
- A = männän tehollinen pinta-ala (m²)
Tehoalueeseen liittyvät näkökohdat
Tehollinen pinta-ala vaihtelee sylinterin tyypin ja suunnan mukaan:
| Sylinterin tyyppi | Laajennusvoimat | Takaisinvetovoima |
|---|---|---|
| Yksitoiminen | P × A | Vain jousivoima |
| Kaksitoiminen (vakio) | P × A | P × (A - a) |
| Kaksitoiminen (sauvaton) | P × A | P × A |
Missä:
- A = männän koko pinta-ala
- a = sauvan poikkipinta-ala
Konsultoin kerran ohiolaista tuotantolaitosta, jonka puristussovelluksen voima oli riittämätön. Heidän laskelmansa näyttivät paperilla oikeilta, mutta todellinen suorituskyky oli puutteellinen. Tutkittuani asiaa sain selville, että he käyttivät mittaripaine2 laskelmissa absoluuttisen paineen sijasta, eivätkä he olleet ottaneet huomioon sauvan pinta-alaa sisäänvedon aikana. Kun laskelmat oli tehty uudelleen oikealla kaavalla ja painearvoilla, pystyimme mitoittamaan heidän järjestelmänsä oikein ja lisäämään tuottavuutta 23%:llä.
Käytännön voiman laskentaesimerkkejä
Tutkitaanpa joitakin reaalimaailman laskelmia:
Esimerkki 1: Venytysvoima vakiosylinterissä
Sylinterille, jossa on:
- Poran halkaisija = 50mm (säde = 25mm = 0,025m).
- Käyttöpaine = 6 bar (600 000 Pa)
Männän alue on:
A = π × r² = π × (0,025)² = 0,001963 m².
Laajennusvoima on:
F = P × A = 600 000 Pa × 0,001963 m² = 1 178 N ≈ 118 kg voima.
Esimerkki 2: Takaisinvetovoima samassa sylinterissä
Jos sauvan halkaisija on 20 mm (säde = 10 mm = 0,01 m):
Sauvojen alue on:
a = π × r² = π × (0,01)² = 0,000314 m².
Tehokas vetäytymisalue on:
A - a = 0,001963 - 0,000314 = 0,001649 m².
Takaisinvetovoima on:
F = P × (A - a) = 600 000 Pa × 0,001649 m² = 989 N ≈ 99 kg voima.
Tehokkuustekijät reaalimaailman sovelluksissa
Käytännön sovelluksissa useat tekijät vaikuttavat teoreettiseen voiman laskentaan:
Kitkahäviöt
Männän tiivisteen ja sylinterin seinämän välinen kitka vähentää tehokasta voimaa:
| Tiivisteen tyyppi | Tyypillinen hyötysuhde |
|---|---|
| Standardi NBR | 0.85-0.90 |
| Vähän kitkaa aiheuttava PTFE | 0.90-0.95 |
| Vanhentuneet/kuluneet tiivisteet | 0.70-0.85 |
Käytännön voimayhtälö
Tarkempi reaalimaailman voimayhtälö on:
F_todellinen = η × P × A
Missä:
- η (eta) = hyötysuhdekerroin (tyypillisesti 0,85-0,95).
Mikä on ilmavirran ja sylinterien paineen suhde?
Virtausnopeuden ja paineen välisen suhteen ymmärtäminen on ratkaisevan tärkeää ilmansyöttöjärjestelmien mitoituksessa ja sylinterin nopeuden ennustamisessa.
Pneumaattisissa järjestelmissä ilmavirta ja paine ovat käänteisessä suhteessa toisiinsa - kun paine kasvaa, virtaus yleensä pienenee. Tämä suhde noudattaa kaasulakeja, ja siihen vaikuttavat rajoitukset, lämpötila ja järjestelmän tilavuus. Sylinterin asianmukainen toiminta edellyttää näiden tekijöiden tasapainottamista halutun nopeuden ja voiman saavuttamiseksi.
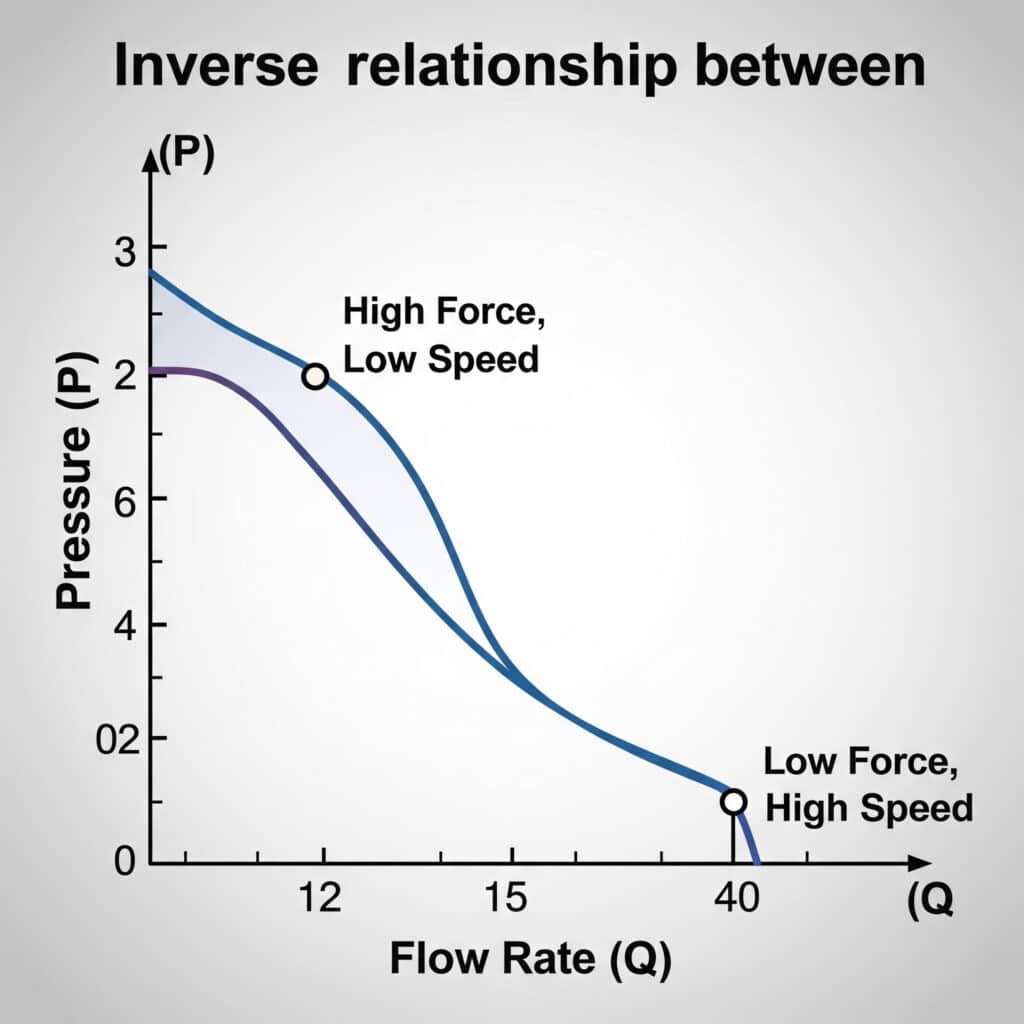
Virtauksen ja paineen muuntotaulukko
Tässä käytännönläheisessä vertailutaulukossa esitetään virtausnopeuden ja painehäviön suhde järjestelmän eri komponenttien välillä:
| Putken koko (mm) | Virtausnopeus (l/min) | Painehäviö (bar/metri) 6 baarin syötöllä |
|---|---|---|
| 4 | 100 | 0.15 |
| 4 | 200 | 0.45 |
| 4 | 300 | 0.90 |
| 6 | 200 | 0.08 |
| 6 | 400 | 0.25 |
| 6 | 600 | 0.50 |
| 8 | 400 | 0.06 |
| 8 | 800 | 0.18 |
| 8 | 1200 | 0.35 |
| 10 | 600 | 0.04 |
| 10 | 1200 | 0.12 |
| 10 | 1800 | 0.24 |
Virtauksen ja paineen matematiikka
Virtauksen ja paineen välinen suhde noudattaa useita kaasulakeja:
Poiseuillen yhtälö3 laminaarista virtausta varten
Laminaarinen virtaus putkien läpi:
Q = (π × r⁴ × ΔP) / (8 × η × L).
Missä:
- Q = tilavuusvirta
- r = putken säde
- ΔP = Paine-ero
- η = dynaaminen viskositeetti
- L = Putken pituus
Virtauskerroin (Cv)4 Menetelmä
Venttiilien kaltaisten komponenttien osalta:
Q = Cv × √ΔP
Missä:
- Q = virtausnopeus
- Cv = Virtauskerroin
- ΔP = Painehäviö komponentin yli
Sylinterin nopeuden laskeminen
Pneumaattisen sylinterin nopeus riippuu virtausnopeudesta ja sylinterin pinta-alasta:
v = Q / A
Missä:
- v = sylinterin nopeus (m/s)
- Q = virtausnopeus (m³/s)
- A = männän pinta-ala (m²)
Eräässä hiljattain Ranskassa sijaitsevassa pakkauslaitoksessa toteutetussa projektissa törmäsin tilanteeseen, jossa asiakkaan sauvaton sylinteri liikkui liian hitaasti riittävästä paineesta huolimatta. Analysoimalla heidän järjestelmäänsä virtaus-painelaskelmiemme avulla havaitsimme alimitoitetut syöttölinjat, jotka aiheuttivat merkittävää painehäviötä. Kun 6 mm:n putkistosta siirryttiin 10 mm:n putkistoon, sykliaika parani 40%, mikä lisäsi tuotantokapasiteettia huomattavasti.
Kriittiset virtausnäkökohdat
Pneumaattisten järjestelmien virtauksen ja paineen väliseen suhteeseen vaikuttavat useat tekijät:
Tukahdutetun virtauksen ilmiö5
Kun painesuhde ylittää kriittisen arvon (noin 0,53 ilmalle), virtaus "tukkeutuu" eikä se voi kasvaa riippumatta virtaussuunnan jälkeisestä paineen alentamisesta.
Lämpötilan vaikutukset
Lämpötila vaikuttaa virtausnopeuteen seuraavan suhteen mukaisesti:
Q₂ = Q₁ × √(T₂/T₁).
Missä:
- Q₁, Q₂ = virtausnopeudet eri lämpötiloissa.
- T₁, T₂ = absoluuttiset lämpötilat.
Miksi paineyksikön muuntamisen ymmärtäminen on tärkeää järjestelmän suunnittelussa?
Maailmanlaajuisesti käytettävien eri paineyksiköiden tuntemus on tärkeää järjestelmän asianmukaisen suunnittelun ja kansainvälisen yhteensopivuuden kannalta.
Paineyksiköiden muuntaminen on tärkeää, koska pneumatiikkakomponenteissa ja eritelmissä käytetään eri yksiköitä alueesta ja toimialasta riippuen. Yksiköiden virheellinen tulkinta voi johtaa merkittäviin laskuvirheisiin, joilla voi olla vaarallisia seurauksia. Absoluuttisen paineen, ylipaineen ja paine-eron välinen muuntaminen lisää monimutkaisuutta entisestään.
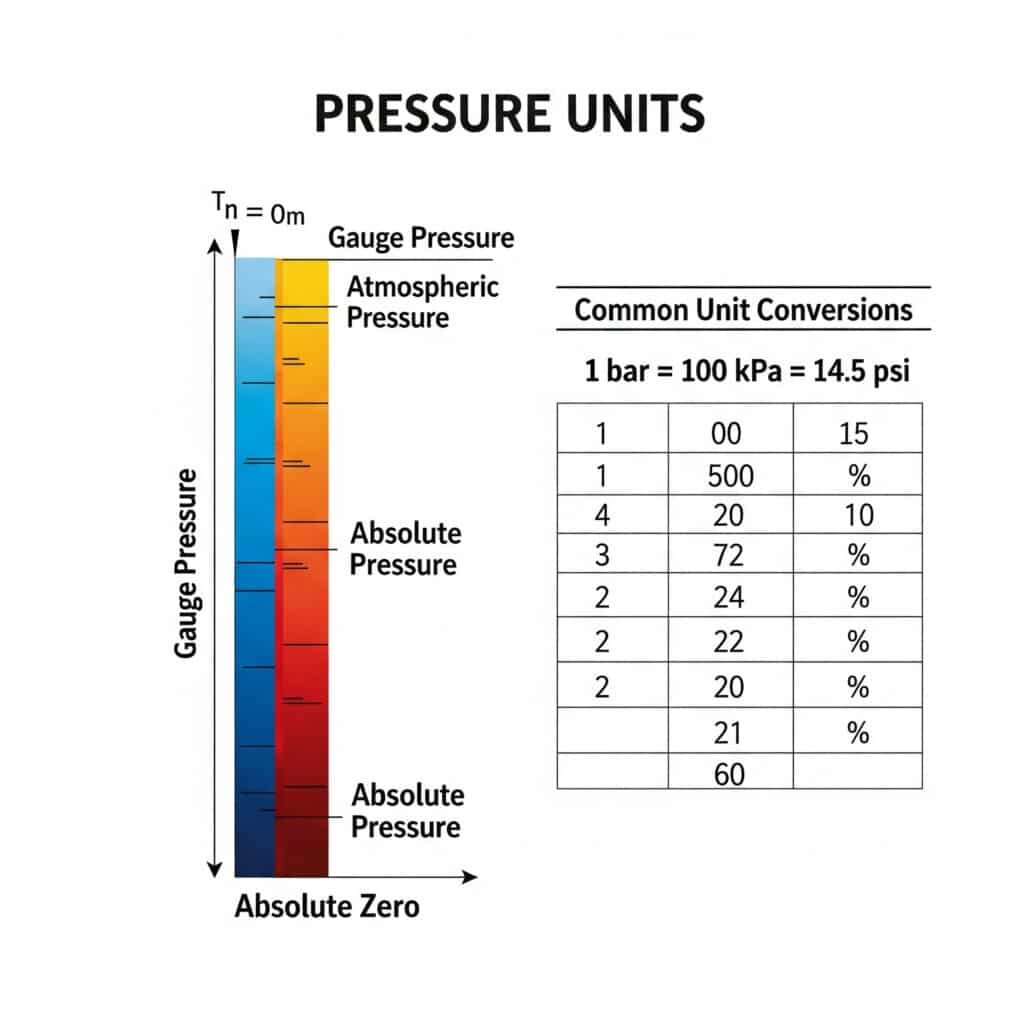
Absoluuttisen paineen yksikkömuunnosopas
Tämä kattava muuntotaulukko auttaa navigoimaan eri paineyksiköissä, joita käytetään maailmanlaajuisesti:
| Yksikkö | Symboli | Vastaavuus Pa:na | Vastaava barina | Vastaavuus psi:nä |
|---|---|---|---|---|
| Pascal | Pa | 1 | 1 × 10-⁵ | 1.45 × 10-⁴ |
| Baari | baari | 1 × 10⁵ | 1 | 14.5038 |
| Punta per neliötuuma | psi | 6,894.76 | 0.0689476 | 1 |
| Kilovoima neliösenttimetriä kohti | kgf/cm² | 98,066.5 | 0.980665 | 14.2233 |
| Megapascal | MPa | 1 × 10⁶ | 10 | 145.038 |
| Tunnelma | atm | 101,325 | 1.01325 | 14.6959 |
| Torr | Torr | 133.322 | 0.00133322 | 0.0193368 |
| Elohopeamillimetri | mmHg | 133.322 | 0.00133322 | 0.0193368 |
| Tuumaa vettä | inH₂O | 249.089 | 0.00249089 | 0.0361274 |
Absoluuttinen vs. mittaripaine
Absoluuttisen paineen ja ylipaineen välisen eron ymmärtäminen on olennaista:
Paineen muunnoslaskin
Paineen yksikkömuunnin
Sylinterin virtausnopeuden muunnin
Muuntokaavat
- P_absoluuttinen = P_mittari + P_ilmakehä + P_ilmakehä
- P_gauge = P_absoluuttinen - P_atmosfäärinen
Kun vakioilmanpaine on noin:
- 1,01325 bar
- 14,7 psi
- 101,325 Pa
Työskentelin kerran saksalaisen insinööritiimin kanssa, joka oli ostanut sauvattomat sylinterimme, mutta ilmoitti, etteivät ne tuottaneet odotettua voimaa. Vianmäärityksen jälkeen selvisi, että he käyttivät voimakaavioitamme (jotka perustuivat mittarinpaineeseen), mutta syöttivät absoluuttisen paineen arvot. Tämä yksinkertainen väärinkäsitys aiheutti 1 barin laskuvirheen heidän voimaodotuksissaan. Paineviitteen selventämisen jälkeen heidän järjestelmänsä toimi täsmälleen määritellysti.
Käytännön muunnosesimerkkejä
Käydään läpi joitakin yleisiä muunnostilanteita:
Esimerkki 1: Työpaineen muuntaminen eri yksiköiden välillä
Sylinteri, joka on mitoitettu 0,7 MPa:n enimmäiskäyttöpaineelle:
Baarissa:
0,7 MPa × 10 bar/MPa = 7 bar
Psi:ssä:
0,7 MPa × 145,038 psi/MPa = 101,5 psi.
Esimerkki 2: muuntaminen mittaripaineesta absoluuttiseksi paineeksi
Järjestelmä, joka toimii 6 baarin ylipaineella:
Absoluuttisena paineena (bar):
6 bar_gauge + 1,01325 bar_atmosfäärinen = 7,01325 bar_absoluuttinen bar.
Esimerkki 3: Muunnos kgf/cm²:stä MPa:ksi
Japanilainen sylinteri, joka on määritelty 7 kgf/cm²:lle:
MPa:
7 kgf/cm² × 0,0980665 MPa/(kgf/cm²) = 0,686 MPa.
Alueelliset paineyksikköpreferenssit
Eri alueilla käytetään yleensä eri paineyksiköitä:
| Alue | Yleiset paineyksiköt |
|---|---|
| Pohjois-Amerikka | psi, inHg, inH₂O |
| Eurooppa | bar, Pa, mbar |
| Japani | kgf/cm², MPa |
| Kiina | MPa, bar |
| UK | bar, psi, Pa |
Paineen mittaus dokumentoinnissa
Painevaatimuksia dokumentoitaessa on tärkeää ilmoittaa selkeästi:
- Numeerinen arvo
- Mittayksikkö
- Olipa kyseessä mittari- (g) tai absoluuttinen (a) paine.
Esimerkiksi:
- 6 bar_g (ylipaine, 6 baaria yli ilmakehän).
- 7,01 bar_a (absoluuttinen paine, kokonaispaine mukaan lukien ilmakehän paine)
Päätelmä
Pneumaattisten sylintereiden taustalla olevan fysiikan ymmärtäminen - Pascalin lain voimalaskelmista virtauksen ja paineen suhteisiin ja paineyksiköiden muuntamiseen - on olennaista järjestelmän asianmukaisen suunnittelun ja vianmäärityksen kannalta. Nämä perusperiaatteet auttavat varmistamaan, että pneumatiikkajärjestelmät tuottavat odotetun suorituskyvyn luotettavasti ja tehokkaasti.
Pneumaattisten järjestelmien fysiikkaa koskevat usein kysytyt kysymykset
Miten lasken sauvattoman pneumaattisen sylinterin voimantuoton?
Sauvattoman pneumaattisen sylinterin voimantuotto lasketaan kertomalla käyttöpaine männän tehollisella pinta-alalla (F = P × A). Esimerkiksi sauvaton sylinteri, jossa on 50 mm:n reikä (0,001963 m²:n pinta-ala) ja joka toimii 6 baarin (600 000 Pa) paineella, tuottaa noin 1 178 N:n voiman. Toisin kuin perinteisillä sylintereillä, sauvattomilla sylintereillä on yleensä sama tehollinen pinta-ala molempiin suuntiin.
Miten lasken sauvattoman pneumaattisen sylinterin voimantuoton?
Sauvattoman pneumaattisen sylinterin voimantuotto lasketaan kertomalla käyttöpaine männän tehollisella pinta-alalla (F = P × A). Esimerkiksi sauvaton sylinteri, jossa on 50 mm:n reikä (0,001963 m²:n pinta-ala) ja joka toimii 6 baarin (600 000 Pa) paineella, tuottaa noin 1 178 N:n voiman. Toisin kuin perinteisillä sylintereillä, sauvattomilla sylintereillä on yleensä sama tehollinen pinta-ala molempiin suuntiin.
Mitä eroa on ylipaineella ja absoluuttisella paineella?
Mittaripaine (bar_g, psi_g) mittaa painetta suhteessa ilmanpaineeseen, jolloin ilmanpaine on nolla. Absoluuttinen paine (bar_a, psi_a) mittaa painetta suhteessa täydelliseen tyhjiöön, joka on nolla. Jos haluat muuntaa mittaripaineen absoluuttiseksi paineeksi, lisää ilmakehän paine (noin 1,01325 bar tai 14,7 psi) mittarilukemaan.
Miten ilmavirta vaikuttaa sylinterin nopeuteen?
Sylinterin nopeus on suoraan verrannollinen ilmavirtaan ja kääntäen verrannollinen männän pinta-alaan (v = Q/A). Riittämätön virtausnopeus, joka johtuu alimitoitetuista syöttölinjoista, rajoittavista liittimistä tai riittämättömistä venttiileistä, rajoittaa sylinterin nopeutta paineesta riippumatta. Esimerkiksi virtausnopeus 20 litraa sekunnissa sylinterin läpi, jonka männän pinta-ala on 0,002 m², tuottaa nopeuden 10 metriä sekunnissa.
Miksi pneumaattiset sylinterit liikkuvat joskus laskettua hitaammin?
Pneumaattiset sylinterit voivat liikkua laskettua hitaammin useiden tekijöiden vuoksi: painehäviöitä aiheuttavat ilmansyötön rajoitukset, tiivisteiden aiheuttama sisäinen kitka, laskelmat ylittävät mekaaniset kuormitukset, tehollista painetta alentavat vuodot tai lämpötilan vaikutus ilman tiheyteen. Lisäksi venttiilien virtauskertoimet rajoittavat usein sylinterin käytettävissä olevaa todellista virtausnopeutta.
Miten muunnan eri paineyksiköiden välillä kansainvälisiä eritelmiä varten?
Muunna paineyksiköiden välillä käyttämällä kertoimia: 1 bar = 100 000 Pa = 0,1 MPa = 14,5038 psi = 1,01972 kgf/cm². Tarkista aina, onko paine ilmoitettu mitta- vai absoluuttisena, sillä tämä ero voi vaikuttaa merkittävästi laskelmiin. Esimerkiksi 6 bar_g vastaa 7,01325 bar_a:ta vakioilmakehän olosuhteissa.
Mikä on sylinterin läpimitan ja voimantuoton välinen suhde?
Sylinterin läpimitan ja voimantuoton välinen suhde on kvadraattinen - läpimitan kaksinkertaistaminen lisää voimantuoton nelinkertaiseksi (koska pinta-ala = π × r²). Esimerkiksi 6 baarin käyttöpaineessa 40 mm:n sylinteri tuottaa noin 754 N:n voiman, kun taas 80 mm:n sylinteri tuottaa noin 3 016 N:n voiman, mikä on lähes nelinkertainen määrä.
-
Selitetään yksityiskohtaisesti Pascalin laki, joka on hydraulisen ja pneumaattisen voimansiirron perustana oleva fluidimekaniikan perusperiaate. ↩
-
Tarjoaa selkeän määritelmän ja vertailun mittari- ja absoluuttisen paineen välillä, mikä on kriittinen ero tarkkojen teknisten laskelmien kannalta, sillä mittari- ja absoluuttinen paine on suhteellinen ilmanpaineeseen nähden. ↩
-
Selitetään Poiseuillen lain johtaminen ja soveltaminen. Laki kuvaa painehäviötä, joka syntyy, kun kokoonpuristumaton ja newtonilainen neste virtaa pitkän sylinterimäisen putken läpi laminaarisessa tilassa. ↩
-
Tarjoaa teknisen määritelmän virtauskertoimelle (Cv), joka on brittiläinen mitta, jonka avulla voidaan vertailla standardoidusti eri venttiilien virtauskapasiteettia. ↩
-
Tutustutaan yksityiskohtaisesti tukahdutetun virtauksen fysiikkaan, joka on nestedynamiikan ehto, joka rajoittaa kokoonpuristuvan nesteen massavirtausta rajoituksen läpi, kun nopeus saavuttaa äänen nopeuden. ↩



