Jokaisen kunnossapitoinsinöörin painajainen on odottamaton laitevika. Kun koneet värähtelevät niiden ominaistaajuudella, katastrofaalinen vaurio voi tapahtua muutamassa minuutissa. Olen nähnyt tämän ongelman maksavan yrityksille tuhansia seisokkiaikoja.
Värähtelyresonanssi1 tapahtuu, kun ulkoinen voima vastaa järjestelmän ominaistaajuutta, mikä aiheuttaa voimistuneita värähtelyjä, jotka voivat vahingoittaa laitteita. Tämän ilmiön ymmärtäminen ja hallinta on olennaista vikojen ehkäisemiseksi ja koneiden käyttöiän pidentämiseksi.
Kerronpa lyhyen tarinan. Viime vuonna eräs saksalainen asiakas soitti minulle paniikissa. Heidän tuotantolinjansa oli pysähtynyt, koska sauvaton sylinteri värähteli rajusti. Mikä oli ongelma? Resonanssi. Tämän artikkelin lopussa ymmärrät, miten voit tunnistaa ja ehkäistä vastaavat ongelmat järjestelmissäsi.
Sisällysluettelo
- Luonnollisen taajuuden kaava: Kuinka voit laskea järjestelmäsi haavoittuvat kohdat?
- Mass-jousi Malli: Miksi tämä yksinkertaistettu lähestymistapa on niin arvokas?
- Vaimennussuhteen optimointi: Mitkä kokeet tuottavat parhaat tulokset?
- Päätelmä
- Usein kysytyt kysymykset värähtelyresonanssista
Luonnollisen taajuuden kaava: Kuinka voit laskea järjestelmäsi haavoittuvat kohdat?
Laitteesi ominaistaajuuden ymmärtäminen on ensimmäinen askel resonanssiongelmien ehkäisemiseksi. Tämä kriittinen arvo määrittää, milloin järjestelmäsi on alttiimpana värähtelyongelmille.
The ominaistaajuus2 (fn) voidaan laskea kaavalla: fn = (1/2π) × √(k/m), jossa k on jäykkyyskerroin ja m on massa. Tämä laskutoimitus paljastaa taajuuden, jolla järjestelmä resonoi, jos sitä jännitetään vastaavilla ulkoisilla voimilla.
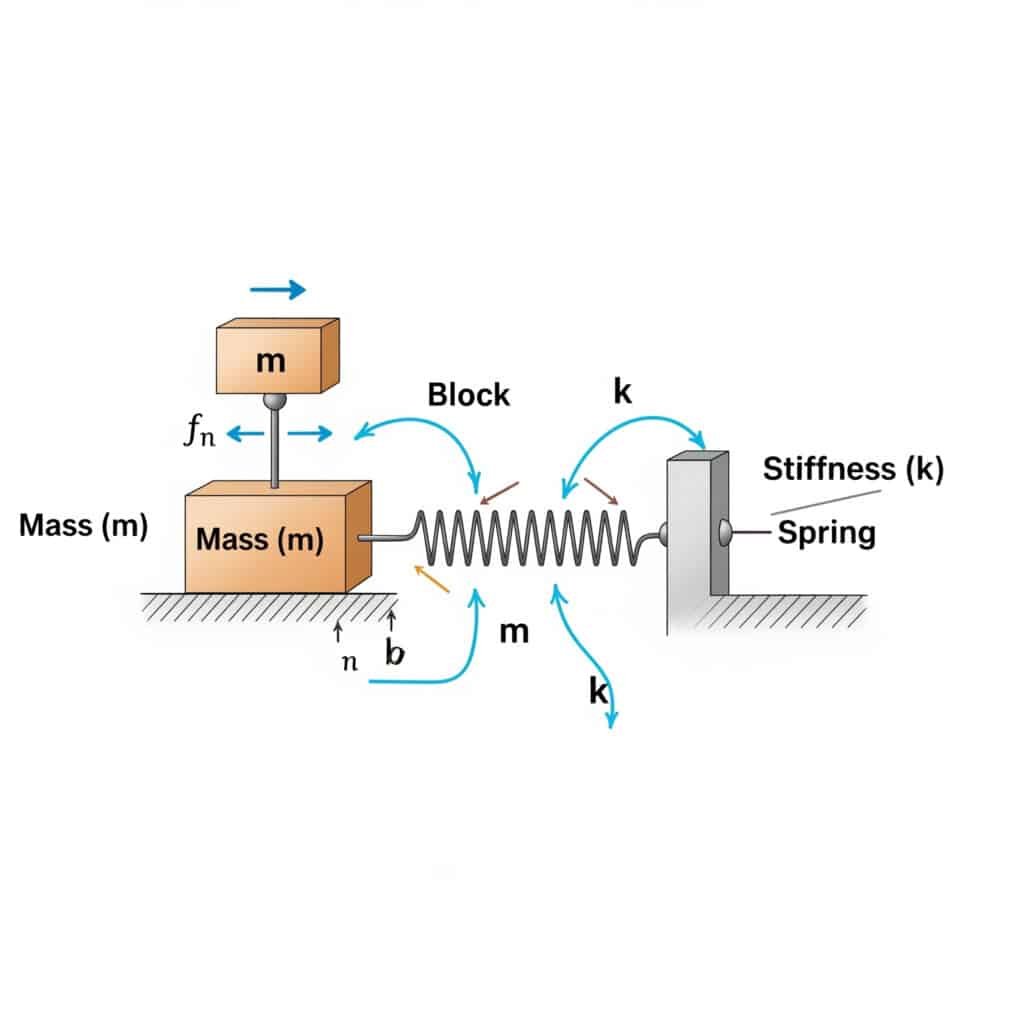
Vieraillessani eräässä sveitsiläisessä tuotantolaitoksessa huomasin, että niiden sauvattomat pneumaattiset sylinterit rikkoutuivat ennenaikaisesti. Heidän huoltotiiminsä ei ollut laskenut niiden asennuksen ominaistaajuutta. Sovellettuamme tätä kaavaa havaitsimme, että heidän käyttönopeutensa oli vaarallisen lähellä järjestelmän ominaistaajuutta.
Ominaistaajuuslaskelmien käytännön sovellukset
Ominaistaajuuden kaava ei ole vain teoreettinen, vaan sillä on suoria sovelluksia erilaisissa teollisuusympäristöissä:
- Laitteiden valinta: Valitaan komponentteja, joiden ominaistaajuudet ovat kaukana käyttöolosuhteista
- Ennaltaehkäisevä huolto: Tarkastusten ajoittaminen tärinäriskiprofiilien perusteella
- Vianmääritys: Odottamattoman tärinän perimmäisen syyn tunnistaminen
Teollisuuskomponenttien yleiset ominaistaajuusarvot
| Komponentti | Tyypillinen ominaistaajuusalue (Hz) |
|---|---|
| Sauvattomat sylinterit | 10-50 Hz |
| Asennustelineet | 20-100 Hz |
| Tukirakenteet | 5-30 Hz |
| Säätöventtiilit | 40-200 Hz |
Ominaistaajuuteen vaikuttavat kriittiset tekijät
Ominaistaajuuden laskeminen vaikuttaa yksinkertaiselta, mutta useat tekijät voivat vaikeuttaa todellisia sovelluksia:
- Epätasainen massan jakautuminen: Useimmilla teollisuuden komponenteilla ei ole täydellisesti jakautunutta massaa.
- Muuttuva jäykkyys: Komponenttien jäykkyys voi vaihdella eri suuntiin.
- Liitäntäpisteet: Komponenttien asennustapa vaikuttaa merkittävästi niiden tärinäominaisuuksiin.
- Lämpötilan vaikutukset: Sekä massa- että jäykkyysominaisuudet voivat muuttua lämpötilan mukaan.
Mass-jousi Malli: Miksi tämä yksinkertaistettu lähestymistapa on niin arvokas?
Massa-jousi-malli tarjoaa intuitiiviset puitteet monimutkaisten värähtelyjärjestelmien ymmärtämiseen. Se pelkistää monimutkaiset koneet peruselementteihin, joita insinöörien on helppo analysoida.
The massa-jousi-malli3 yksinkertaistaa värähtelyanalyysia esittämällä mekaaniset järjestelmät erillisinä massoina, jotka on yhdistetty jousilla. Tämän lähestymistavan avulla insinöörit voivat ennustaa järjestelmän käyttäytymistä, tunnistaa mahdolliset resonanssiongelmat ja kehittää tehokkaita ratkaisuja ilman monimutkaista matematiikkaa.
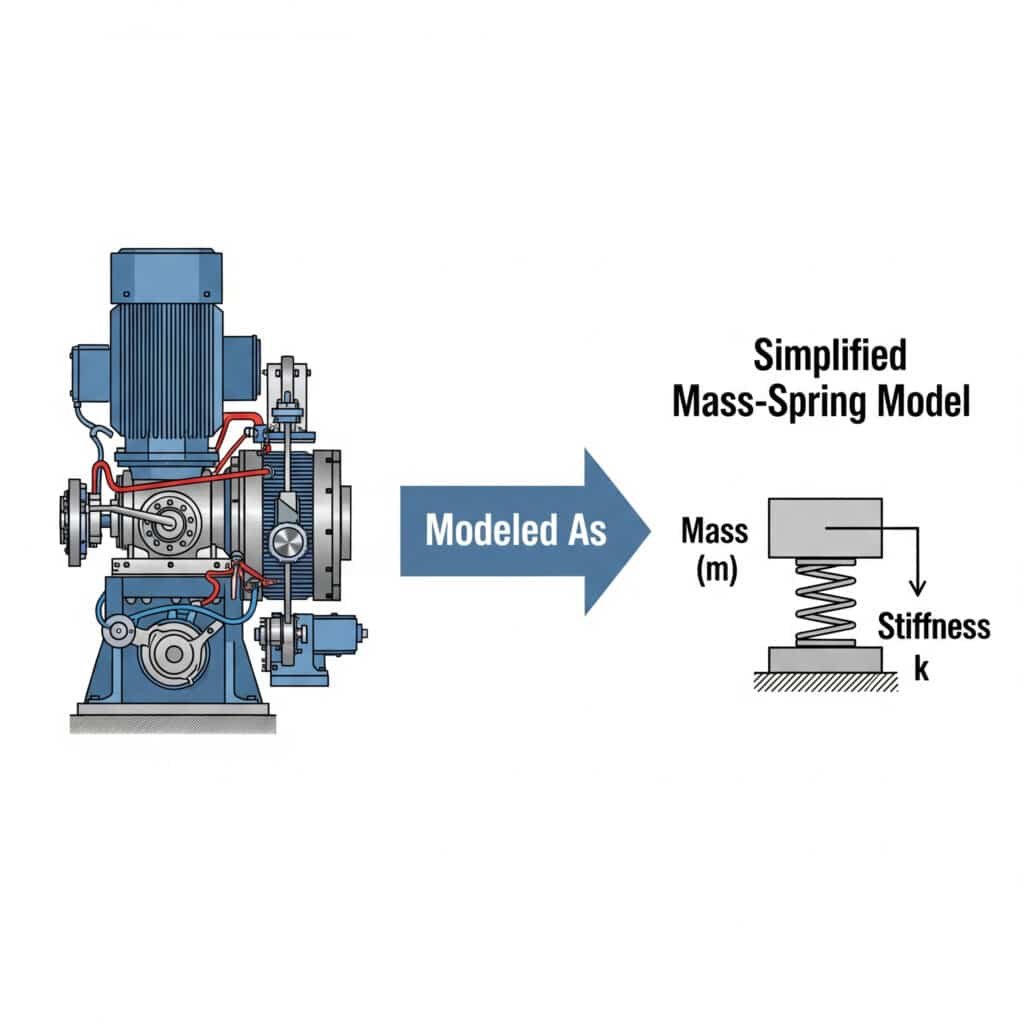
Muistan työskennelleeni erään Michiganissa toimivan autonosien valmistajan kanssa, joka ei voinut ymmärtää, miksi heidän ohjaamansa sauvattomat sylinterit eivät toimineet. Mallintamalla heidän järjestelmäänsä yksinkertaisena massa-jousi -järjestelynä havaitsimme, että kiinnityskannattimet toimivat tahattomina jousina ja loivat resonanssitilan.
Todellisten järjestelmien muuntaminen massajousimalleiksi
Voit soveltaa tätä lähestymistapaa laitteisiisi:
- Tunnistetaan tärkeimmät massat: Määritä, mitkä komponentit vaikuttavat merkittävästi painoon
- Jousielementtien paikantaminen: Etsi komponentteja, jotka varastoivat ja vapauttavat energiaa (varsinaiset jouset, joustavat kiinnikkeet jne.).
- Karttayhteydet: Dokumentoi, miten massat ja jouset ovat vuorovaikutuksessa keskenään
- Yksinkertaista: Yhdistetään samankaltaisia elementtejä hallittavissa olevan mallin luomiseksi.
Massajousijärjestelmien tyypit
| Järjestelmätyyppi | Kuvaus | Yleiset sovellukset |
|---|---|---|
| Yksi DOF | Yksi massa ja yksi jousi | Yksinkertaiset pneumaattiset sylinterit |
| Multi-DOF | Useita massoja ja useita jousia | Monimutkaiset koneet, joissa on useita osia |
| Jatkuva | Ääretön DOF (vaatii eri analyysin) | Palkit, levyt ja kuoret |
Edistyneen mallintamisen näkökohdat
Vaikka massajousen perusmalli on arvokas, useat parannukset tekevät siitä realistisemman:
- Vaimentimien lisääminen: Todellisissa järjestelmissä on aina energiahäviöitä
- Epälineaarisuuden huomioon ottaminen: Jouset eivät aina seuraa Hooken laki4 täydellisesti
- Pakotetun tärinän huomioon ottaminen: Ulkoiset voimat muuttavat järjestelmän käyttäytymistä
- Kytkentävaikutukset mukaan luettuina: Liike yhteen suuntaan voi vaikuttaa muihin suuntiin
Vaimennussuhteen optimointi: Mitkä kokeet tuottavat parhaat tulokset?
Vaimennus on paras puolustus resonanssiongelmia vastaan. Optimaalisen vaimennussuhteen löytäminen kokeilemalla voi parantaa järjestelmän suorituskykyä ja luotettavuutta huomattavasti.
Vaimennussuhde5 optimointikokeissa testataan systemaattisesti erilaisia vaimennuskokoonpanoja ihanteellisen tasapainon löytämiseksi tärinänhallinnan ja järjestelmän reagointikyvyn välillä. Optimaalinen vaimennussuhde on tyypillisesti 0,2 ja 0,7 välillä, jolloin tärinänvaimennus on riittävä ilman liiallista energian menetystä.
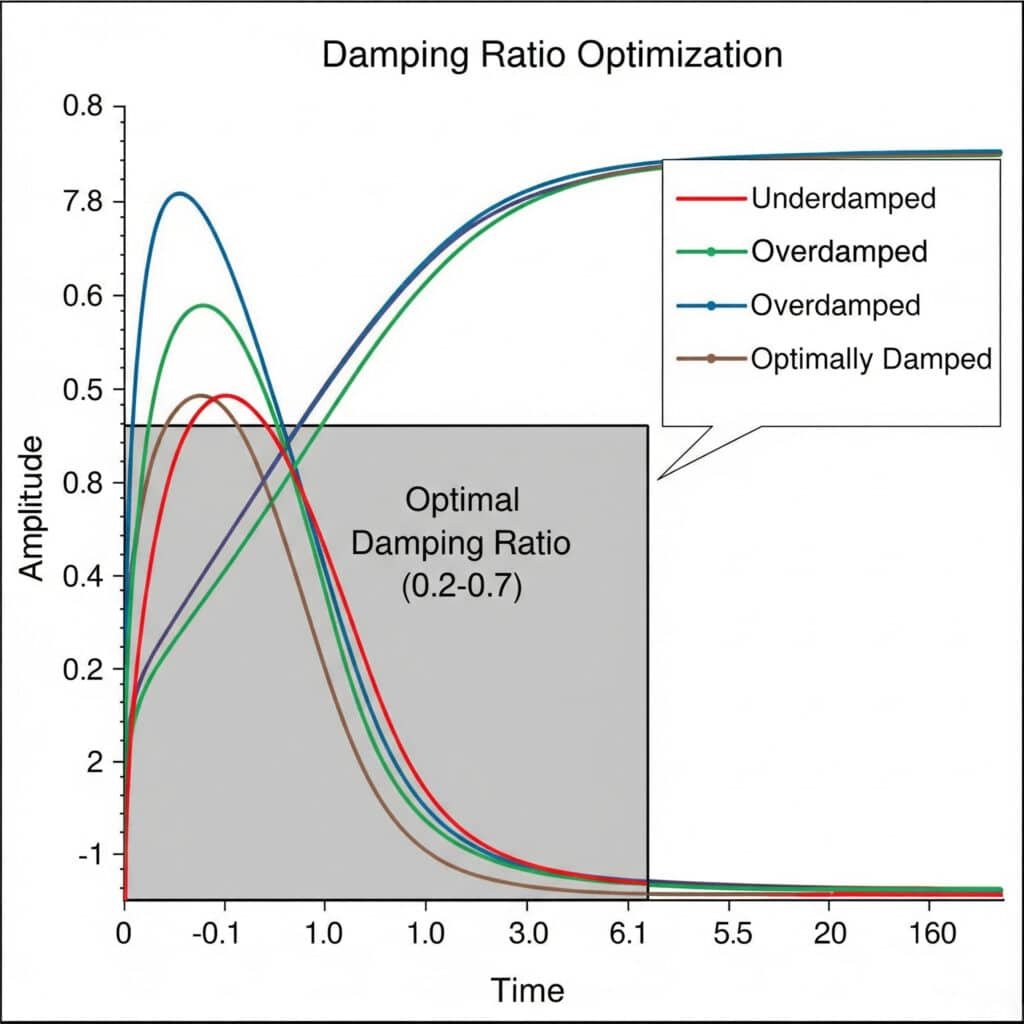
Viime kuussa autoin ranskalaista elintarviketeollisuuden laitevalmistajaa ratkaisemaan magneettisten sauvattomien sylinterien jatkuvat tärinäongelmat. Vaimennussuhdekokeiden avulla havaitsimme, että heidän alkuperäisen rakenteensa vaimennussuhde oli vain 0,05 - aivan liian alhainen resonanssiongelmien estämiseksi.
Koejärjestely vaimennussuhteen testausta varten
Tehokkaiden vaimennuksen optimointikokeiden suorittaminen:
- Perusmittaus: Tallenna järjestelmän vaste ilman lisävaimennusta
- Inkrementaalinen testaus: Lisää vaimennuselementtejä hallitusti
- Vastausmittaus: Mittaa amplitudi, asettumisaika ja taajuusvaste.
- Tietojen analysointi: Laske vaimennussuhde kullekin kokoonpanolle
- Validointi: Tarkista suorituskyky todellisissa käyttöolosuhteissa
Vaimennustekniikoiden vertailu
| Vaimennustekniikka | Edut | Rajoitukset | Tyypilliset sovellukset |
|---|---|---|---|
| Viskoosiset vaimentimet | Ennustettava suorituskyky, vakaa lämpötila | Vaatii huoltoa, mahdolliset vuodot | Raskaat koneet, tarkkuuslaitteet |
| Kitkavaimentimet | Yksinkertainen rakenne, kustannustehokas | Kuluminen ajan myötä, epälineaarinen käyttäytyminen | Rakenteelliset tuet, peruskoneet |
| Materiaalin vaimennus | Ei liikkuvia osia, kompakti | Rajoitettu säätöalue | Tarkkuusinstrumentit, tärinäneristys |
| Aktiivinen vaimennus | Sopeutuu muuttuviin olosuhteisiin | Monimutkainen, vaatii virtaa | Kriittiset sovellukset, muuttuvanopeuksiset laitteet |
Vaimennuksen optimointi eri käyttöolosuhteisiin
Ihanteellinen vaimennussuhde ei ole yleispätevä - se riippuu sovelluksestasi:
- Nopeat toiminnot: Pienemmät vaimennussuhteet (0,1-0,3) säilyttävät herkkyysominaisuudet.
- Tarkkuus sovellukset: Suuremmat vaimennussuhteet (0,5-0,7) lisäävät vakautta.
- Muuttuvan kuormituksen järjestelmät: Mukautuva vaimennus voi olla tarpeen
- Lämpötilaherkät ympäristöt: Harkitse vaimennusmateriaaleja, joilla on vakaat ominaisuudet
Tapaustutkimus: Sylinterin vaimennuksen optimointi
Kun optimoimme kaksitoimisen sauvattoman sylinterin pakkauskoneeseen, testasimme viittä erilaista vaimennuskokoonpanoa:
- Vakio päätytyynyt: Vaimennussuhde = 0,12
- Laajennetut tyynyt: Vaimennussuhde = 0,25
- Ulkoiset iskunvaimentimet: Vaimennussuhde = 0,41
- Komposiittikiinnikkeet: Vaimennussuhde = 0,38
- Yhdistetty lähestymistapa (3+4): Vaimennussuhde = 0,53
Yhdistetty lähestymistapa tarjosi parhaan suorituskyvyn, sillä se vähensi tärinän amplitudia 78% ja säilytti samalla hyväksyttävät vasteajat.
Päätelmä
Värähtelyresonanssin ymmärtäminen ominaistaajuuslaskelmien, massajousien mallintamisen ja vaimennussuhteen optimoinnin avulla on ratkaisevan tärkeää laitteiden vikojen ehkäisemiseksi. Soveltamalla näitä periaatteita voit pidentää koneiden käyttöikää, vähentää seisokkiaikoja ja parantaa järjestelmän yleistä suorituskykyä.
Usein kysytyt kysymykset värähtelyresonanssista
Mitä on värähtelyresonanssi teollisuuslaitteissa?
Värähtelyresonanssi syntyy, kun ulkoinen voima vastaa järjestelmän ominaistaajuutta ja aiheuttaa vahvistuneita värähtelyjä. Teollisuuslaitteissa tämä ilmiö voi johtaa liialliseen liikkeeseen, komponenttien väsymiseen ja katastrofaalisiin vikaantumisiin, jos sitä ei hallita asianmukaisesti.
Miten voin tunnistaa, esiintyykö järjestelmässäni resonanssia?
Etsi oireita, kuten selittämätöntä melun lisääntymistä, näkyvää tärinää tietyillä nopeuksilla, komponenttien ennenaikaisia vikoja ja suorituskyvyn heikkenemistä, joka ilmenee tasaisissa toimintapisteissä. Tärinäanalyysityökalut voivat vahvistaa resonanssiolosuhteet.
Mitä eroa on pakotetulla värähtelyllä ja resonanssilla?
Pakotettua värähtelyä esiintyy aina, kun ulkoinen voima vaikuttaa järjestelmään, kun taas resonanssi on erityistilanne, jossa pakottavan voiman taajuus vastaa järjestelmän ominaistaajuutta, mikä johtaa vahvistuneeseen vasteeseen. Kaikessa resonanssissa on kyse pakotetusta värähtelystä, mutta kaikki pakotettu värähtely ei aiheuta resonanssia.
Miten sauvattoman pneumaattisen sylinterin rakenne vaikuttaa sen tärinäominaisuuksiin?
Sauvattomien pneumaattisten sylintereiden rakenne - niiden liikkuva kelkka, sisäinen tiivistysjärjestelmä ja ohjausmekanismit - luo ainutlaatuisia tärinähaasteita. Jatkettu profiili toimii palkkina, joka voi taipua, vaunun massa aiheuttaa inertiavoimia ja tiivistysnauhat voivat aiheuttaa vaihtelevaa kitkaa.
Millä yksinkertaisilla muutoksilla voidaan vähentää olemassa olevien laitteiden resonanssia?
Jos olemassa olevissa laitteissa on resonanssiongelmia, kannattaa harkita massan lisäämistä ominaistaajuuden muuttamiseksi, ulkoisten vaimentimien tai iskunvaimentimien asentamista, asennusmenetelmien muuttamista tärinäneristykseksi tai käyttönopeuksien säätämistä resonanssitaajuuksien välttämiseksi.
-
Tarjoaa perustavanlaatuisen selityksen mekaanisesta resonanssista, usein visuaalisten esimerkkien avulla, ja osoittaa, miten pieni jaksollinen voima voi tuottaa järjestelmässä suuren amplitudin värähtelyjä. ↩
-
Tarjoaa yksityiskohtaisen katsauksen ominaistaajuuden fysiikkaan, eli tiettyyn taajuuteen, jolla systeemi pyrkii värähtelemään, kun mitään ohjaavaa tai vaimentavaa voimaa ei ole. ↩
-
Selittää massa-jousimallin periaatteet, joka on fysiikan ja tekniikan perustavanlaatuinen ideaalikuvaus, jota käytetään analysoimaan monimutkaisia järjestelmiä, joilla on yksinkertaista harmonista liikettä. ↩
-
Hooken laki on fysiikan periaate, jonka mukaan jousen venyttämiseen tai puristamiseen tarvittava voima on suoraan verrannollinen tähän etäisyyteen. ↩
-
Kuvaa vaimennussuhdetta, dimensiotonta mittaa, joka määrittää, miten järjestelmän värähtelyt laantuvat häiriön jälkeen, mikä on kriittinen tekijä resonanssin hallinnassa. ↩


