Miten virtausresistanssi todella vaikuttaa pneumaattisen järjestelmän suorituskykyyn?

Tekninen infografiikka, jossa selitetään virtausvastusta pneumaattisissa järjestelmissä. Siinä on kaavio putkesta, jossa on suora osa ja sen jälkeen mutka. Putken yläpuolelle piirretty kuvaaja osoittaa painetason. Suoran osuuden varrella paine laskee loivasti alaspäin, mikä on merkitty merkinnällä "kitkahäviöt". Mutkan kohdalla paine laskee jyrkästi portaittain, mikä on merkitty "Paikalliset häviöt". Kuvassa erotetaan selvästi nämä kaksi vastuksen tyyppiä ja niiden kumulatiivinen vaikutus paineeseen. — Vastustus todella vaikuttaa

Onko sinulla ongelmia sylinterien hitaiden nopeuksien, epäjohdonmukaisen liikkeen tai riittämättömän voiman kanssa pneumaattisissa järjestelmissäsi? Nämä yleiset ongelmat johtuvat usein väärinymmärretystä syyllisestä: virtausvastuksesta. Monet insinöörit mitoittavat pneumatiikkakomponenttinsa pelkästään paine- ja voimavaatimusten perusteella ja jättävät huomiotta virtausvastuksen kriittisen vaikutuksen todelliseen suorituskykyyn.

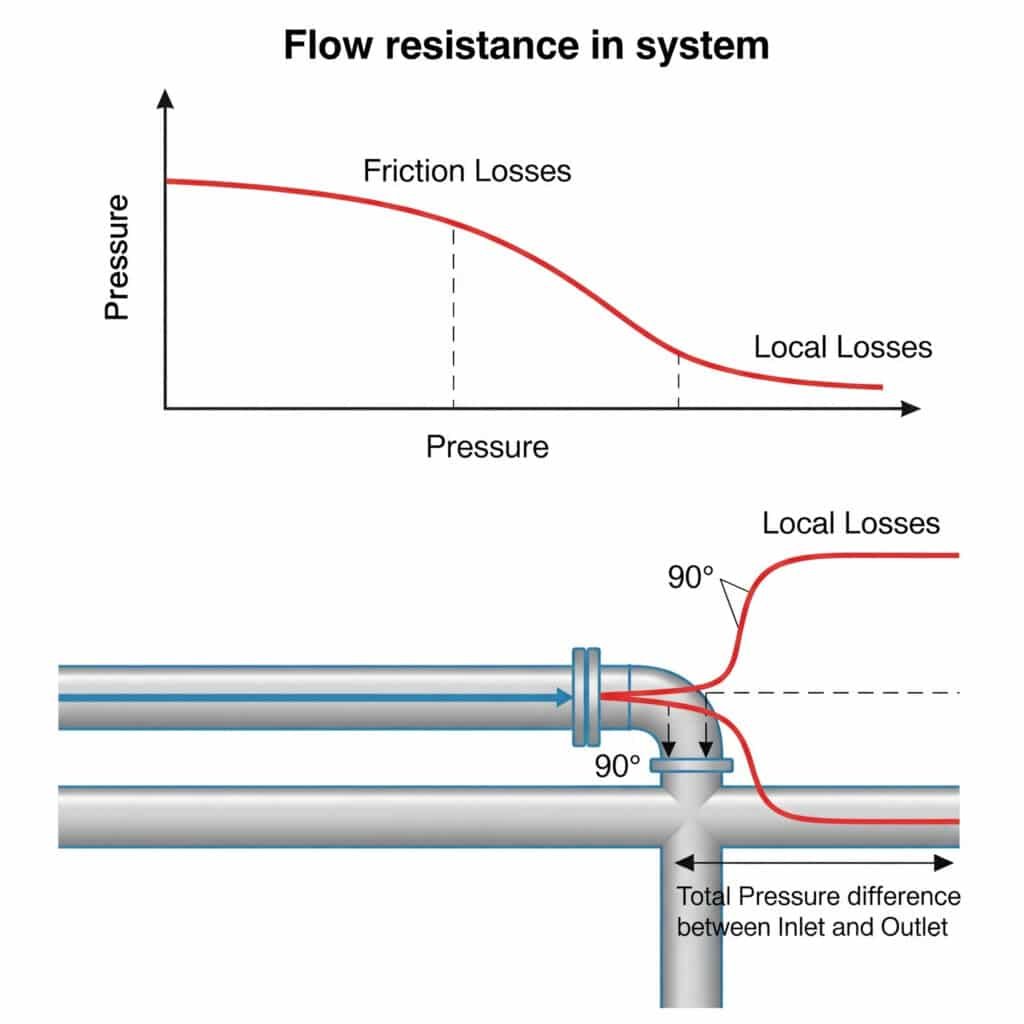
Pneumaattisten järjestelmien virtausvastus aiheuttaa painehäviöitä, jotka vähentävät käytettävissä olevaa voimaa, rajoittavat maksiminopeutta ja aiheuttavat epäjohdonmukaista liikettä. Tämä vastus johtuu sekä kitkasta suorissa putkissa (kitkahäviöt) että häiriöistä liittimissä, mutkissa ja venttiileissä (paikalliset häviöt). Yhdessä nämä vastukset voivat vähentää järjestelmän todellista suorituskykyä 20-50% teoreettisiin laskelmiin verrattuna.

Työskennellessäni yli 15 vuotta Beptolla pneumaattisten järjestelmien parissa olen nähnyt lukemattomia tapauksia, joissa virtausvastuksen ymmärtäminen ja käsitteleminen on muuttanut vajaatehoiset järjestelmät luotettaviksi ja tehokkaiksi toiminnoiksi. Kerron, mitä olen oppinut näiden piilevien suorituskyvyn tappajien laskemisesta ja minimoimisesta.

Sisällysluettelo

Miten lasket todellisuudessa pneumaattisten johtojen kitkahäviöt?
Miksi ekvivalenttipituusmenetelmä on kriittinen järjestelmän tarkan suunnittelun kannalta?
Mitä tapahtuu, kun ilma virtaa supistettujen läpivientien läpi?
Päätelmä
Usein kysytyt kysymykset virtausvastuksesta pneumaattisissa järjestelmissä

Miten lasket todellisuudessa pneumaattisten johtojen kitkahäviöt?

Suorien putkien kitkahäviöt ovat virtausvastuksen laskennan perusta, mutta monet insinöörit luottavat liian yksinkertaistettuihin nyrkkisääntöihin, jotka johtavat alimitoitettuihin järjestelmiin.

Pneumaattisten johtojen kitkahäviöt lasketaan käyttäen seuraavaa laskentatapaa Darcy-Weisbachin yhtälö¹: ΔP = λ(L/D)(ρv²/2), jossa λ on kitkakerroin, L on putken pituus, D on putken halkaisija, ρ on ilman tiheys ja v on virtausnopeus. Pneumaattisissa järjestelmissä kitkakerroin λ vaihtelee seuraavasti Reynoldsin luku² ja suhteellinen karheus, ja se määritetään tyypillisesti hakutaulukoiden avulla tai käyttämällä Moody-kaavio³.

Kitkahäviöiden ymmärtämisellä on käytännön vaikutuksia järjestelmän suunnitteluun ja vianmääritykseen. Anna minun pilkkoa tämä käytännönläheisiksi oivalluksiksi.

Kitkakertoimitaulukoiden tehokas käyttö

Kitkakerroin (λ) on keskeinen parametri painehäviöiden laskennassa, mutta sen arvon määrittäminen edellyttää virtausolosuhteiden huomioon ottamista:

Virtausjärjestelmä	Reynoldsin luku (Re)	Kitkakertoimen määrittäminen
Laminaarinen virtaus	Re < 2000	λ = 64/Re
Siirtymävirta	2000 < Re < 4000	Epäluotettava - vältä suunnittelua tällä alueella.
Turbulenttinen virtaus	Re > 4000	Käytä suhteelliseen karheuteen (ε/D) perustuvia hakutaulukoita.

Käytännön kitkakertoimen hakutaulukko

Pneumaattisten järjestelmien turbulenttista virtausta varten käytetään tätä yksinkertaistettua taulukkoa:

Putkimateriaali	Suhteellinen karheus (ε/D)	Kitkakerroin (λ) tavallisilla Reynoldsin luvuilla
		Re = 10,000
Sileät putket (PVC, polyuretaani)	0.0001 – 0.0005	0.031
Alumiiniputket	0.001 – 0.002	0.035
Sinkitty teräs	0.003 – 0.005	0.042
Ruostunut teräs	0.01 – 0.05	0.054

Painehäviön laskeminen todellisissa pneumaattisissa järjestelmissä

Käydään läpi käytännön esimerkki:

Parametri	Arvo/Laskelma	Esimerkki
Putken halkaisija (D)	Sisähalkaisija	8mm (0.008m)
Putken pituus (L)	Suoran kokonaispituus	5m
Virtausnopeus (Q)	Järjestelmävaatimuksista	20 vakiolitraa sekunnissa
Ilman tiheys (ρ)	Käyttöpaineessa	7,2 kg/m³ 6 baarin paineessa
Virtausnopeus (v)	v = Q/(π×D²/4)	v = 0,02m³/s/(π×0,008²/4) = 398 m/s.
Reynoldsin luku (Re)	Re = ρvD/μ	Re = 7,2×398×0,008/1,8×10-⁵ = 1 273 600.
Suhteellinen karheus	Polyuretaaniletkuille	0.0003
Kitkakerroin (λ)	Hakutaulukosta	0.017
Painehäviö (ΔP)	ΔP = λ(L/D)(ρv²/2)	ΔP = 0,017×(5/0,008)×(7,2×398²/2) = 6,07 bar.

Todellisen maailman sovellus: Sylinterin nopeusongelmien ratkaiseminen

Viime vuonna työskentelin Sarahin kanssa, joka oli tuotantoinsinööri Wisconsinissa sijaitsevassa pakkauslaiteyrityksessä. Hänen sauvaton sylinterijärjestelmänsä toimi vain 60%:n nopeudella odotetusta nopeudesta, vaikka sylinteri oli oikein mitoitettu ja syöttöpaine oli riittävä.

Analysoituani hänen järjestelmänsä huomasin, että hän käytti 6 mm:n putkia suurivirtaussovellukseen. Kitkahäviöt aiheuttivat 2,1 barin painehäviön, mikä vähensi merkittävästi käytettävissä olevaa voimaa ja nopeutta. Kun vaihdoimme 10 mm:n putkistoon, painehäviö pieneni 0,4 baariin, ja hänen järjestelmänsä saavutti välittömästi vaaditun suorituskyvyn ilman muita muutoksia.

Kitkahäviöihin vaikuttavat tekijät todellisissa järjestelmissä

Useat tekijät vaikuttavat todellisiin kitkahäviöihin:

Ilman lämpötila: Korkeammat lämpötilat lisäävät viskositeettia ja kitkaa
Saastuminen: Lika ja öljy voivat lisätä tehokasta karheutta
Putkien taivutus: Taivutettujen putkien mikro-muodonmuutokset lisäävät kestävyyttä
Iän heikkeneminen: Korroosio ja saostumat lisäävät karheutta ajan myötä
Käyttöpaine: Suuremmat paineet lisäävät tiheyttä ja häviöitä

Miksi ekvivalenttipituusmenetelmä on kriittinen järjestelmän tarkan suunnittelun kannalta?

Paikalliset häviöt liitososissa, venttiileissä ja mutkissa ovat usein suuremmat kuin kitkahäviöt suorissa putkissa, mutta monet insinöörit joko jättävät ne huomiotta tai käyttävät karkeasti arvioituja menetelmiä, jotka johtavat suorituskykyongelmiin.

Ekvivalenttipituusmenetelmällä muunnetaan liittimistä ja venttiileistä aiheutuvat paikalliset häviöt vastaavaksi suoran putken pituudeksi, joka aiheuttaisi saman painehäviön. Tämä lasketaan käyttämällä Le = K(D/λ), jossa Le on ekvivalentti pituus, K on paikallinen häviökerroin⁴, D on putken halkaisija ja λ on kitkakerroin. Tämä menetelmä yksinkertaistaa laskelmia ja antaa tarkempia ennusteita järjestelmän suorituskyvystä.

Tutkitaan, miten tätä menetelmää voidaan soveltaa tehokkaasti pneumaattisten järjestelmien suunnittelussa.

Yleisten pneumaattisten komponenttien ekvivalenttipituutta koskevat taulukot

Tässä on käytännönläheinen vertailutaulukko yleisimmistä pneumaattisista komponenteista:

Komponentti	K-arvo	Vastaava pituus (Le/D)
90° kyynärpää (terävä)	0.9	30
90° kulma (vakiosäde)	0.3	10
45° kyynärpää	0.2	7
T-liitos (läpivirtaus)	0.3	10
T-liitos (haaravirta)	1.0	33
Palloventtiili (täysin auki)	0.1	3
Porttiventtiili (täysin auki)	0.2	7
Pikaliitäntäkytkin	0.4-0.8	13-27
Takaiskuventtiili	1.5-2.5	50-83
Vakiovirtauksen säätöventtiili	1.0-3.0	33-100

Vastaavan pituuden menetelmän soveltaminen

Tämän menetelmän tehokas käyttö:

Tunnista kaikki pneumatiikkapiirin komponentit
K-arvo tai ekvivalentti pituussuhde (Le/D) kullekin komponentille.
Lasketaan vastaava pituus kertomalla se putken halkaisijalla.
Lisätään kaikki vastaavat pituudet putken todelliseen suoran putken pituuteen.
Käytä tehollista kokonaispituutta kitkahäviölaskelmissa.

Esimerkiksi järjestelmä, jossa on 5 m suoraa 8 mm:n putkea sekä neljä 90°:n kulmakappaletta, yksi T-liitos ja kaksi pikaliitintä:

Komponentti	Määrä	Le/D	Vastaava pituus
90° kulmakappaleet	4	10	4 × 10 × 0,008m = 0,32m.
T-risteys	1	10	1 × 10 × 0,008 m = 0,08 m.
Pikaliittimet	2	20	2 × 20 × 0,008 m = 0,32 m.
Vastaava kokonaispituus			0.72m
Todellinen suora pituus			5.00m
Tehollinen kokonaispituus			5.72m

Tämä tarkoittaa, että 5 metrin järjestelmäsi käyttäytyy itse asiassa kuin 5,72 metrin järjestelmä paikallisten häviöiden vuoksi - 14,4%:n lisäys tehollisessa pituudessa.

Tapaustutkimus: Venttiilien sijoittelun optimointi kokoonpanojärjestelmissä

Autoin hiljattain Miguelia, automaatioinsinööriä arizonalaisessa elektroniikan kokoonpanotehtaassa. Hänen pick-and-place-järjestelmässään esiintyi epäjohdonmukaista liikettä ja syklien keston vaihtelua, vaikka siinä käytettiin korkealaatuisia komponentteja.

Analyysi osoitti, että hänen venttiiliputkistonsa sijaitsi 3 metrin päässä sylintereistä, ja virtapiiriin kuului lukuisia liitoksia. Ekvivalenttipituuslaskenta osoitti, että hänen 3 metrin todellisen etäisyytensä tehollinen pituus oli 7,2 metriä paikallisten häviöiden vuoksi - yli kaksinkertainen suoran putken etäisyyteen verrattuna!

Siirtämällä venttiiliputkiston lähemmäs sylintereitä ja poistamalla useita liitoksia lyhensimme tehollista pituutta 7,2 metristä 2,1 metriin. Tämä pienensi painehäviötä 70%, mikä johti tasaiseen liikkeeseen ja 15%:n lyhennykseen sykliajassa.

Käytännön vinkkejä paikallisten tappioiden minimoimiseksi

Pneumaattisten järjestelmien paikallisten häviöiden vähentämiseksi:

Käytä pyyhkäistyä tai pyöristettyä kyynärpäätä terävien mutkien sijasta (pienentää K-arvoa 67%)
Minimoidaan liitososien määrä suunnittelemalla suorempi reititys
Valitse matalaa rajoitusta aiheuttavat komponentit kuten täysimittaiset palloventtiilit tarvittaessa
Kokoa liitososat oikein - alimitoitetut liitososat aiheuttavat suhteettoman suuria tappioita.
Sijoita venttiilit toimilaitteiden lähelle minimoida letkujen tehollinen pituus

Mitä tapahtuu, kun ilma virtaa supistettujen läpivientien läpi?

Pneumatiikkapiirien pienemmät läpiviennit - kuten osittain suljetut venttiilit, alimitoitetut liittimet tai halkaisijan siirtymät - aiheuttavat merkittäviä virtausrajoituksia, jotka voivat vaikuttaa vakavasti järjestelmän suorituskykyyn.

Kun ilma virtaa pienennettyjen läpivientien läpi, painehäviöt⁵ tapahtuu kaavan ΔP = ρ(v₂² - v₁²)/2 mukaisesti, jossa v₁ on nopeus ennen rajoitusta ja v₂ on nopeus rajoituksessa. Tämä voidaan kompensoida käyttämällä porausasteen kompensointikerrointa C = (1 - (d/D)⁴), jossa d on pienennetty halkaisija ja D on alkuperäinen halkaisija. Tämä kerroin auttaa ennustamaan järjestelmän todellista suorituskykyä ja välttämään komponenttien alimitoitusta.

Tutkitaan, mitä käytännön vaikutuksia pienemmillä läpimitoilla on ja miten ne voidaan ottaa huomioon järjestelmäsuunnittelussa.

Painehäviöiden laskeminen halkaisijan siirtymissä

Kun ilma virtaa suuremmasta halkaisijasta pienempään, painehäviö voidaan laskea käyttämällä:

Parametri	Kaava	Esimerkki
Alkuperäinen halkaisija (D)	Eritelmistä	10mm
Pienennetty halkaisija (d)	Eritelmistä	6mm
Porasuhde (d/D)	Yksinkertainen jako	0.6
Virtausnopeus (Q)	Järjestelmävaatimuksista	15 vakiolitraa sekunnissa
Nopeus alkuperäisessä putkessa (v₁)	v₁ = Q/(π×D²/4)	191 m/s
Nopeus pienennetyssä osassa (v₂)	v₂ = Q/(π×d²/4)	531 m/s
Painehäviö (ΔP)	ΔP = ρ(v₂² - v₁²)/2	0,88 bar
Kompensointikerroin (C)	C = (1 - (d/D)⁴)	0.87

Yleiset poran pienentämisskenaariot ja niiden vaikutukset

Seuraavassa kerrotaan, miten eri läpivientien pienennykset vaikuttavat virtauskapasiteettiin:

Poraus Reduction	Virtauskapasiteetin vähentäminen	Painehäviön kasvu
10mm - 8mm	36%	2.4×
10mm - 6mm	64%	7.7×
10mm - 4mm	84%	39×
8mm - 6mm	44%	3.2×
8mm - 4mm	75%	16×
6mm - 4mm	56%	5.1×

Nämä luvut korostavat, miksi näennäisesti pienillä halkaisijan vähennyksillä voi olla dramaattisia vaikutuksia järjestelmän suorituskykyyn.

Useiden rajoitusten kumulatiivinen vaikutus

Todellisissa pneumaattisissa piireissä esiintyy useita rajoituksia sarjassa. Niiden vaikutus on kumulatiivinen, ja se voidaan laskea käyttämällä:

Muunnetaan kukin rajoitus vastaavaksi C-kertoimeksi.
Lasketaan C-kertoimen kokonaismäärä: Ctotal = 1 - (1-C₁)(1-C₂)(1-C₃)...
Käytä tätä kokonaiskerrointa järjestelmän kokonaissuorituskyvyn alenemisen määrittämiseen.

Tapaustutkimus: Venttiilin ja toimilaitteen yhteensopimattomuusongelmien ratkaiseminen.

Viime kuussa työskentelin Thomasin kanssa, joka on huoltopäällikkö huonekaluja valmistavassa tehtaassa Pohjois-Carolinassa. Hänen uusi sauvaton sylinterijärjestelmänsä toimi alle puolella odotetusta nopeudesta, vaikka siinä käytettiin valmistajan suosittelemaa venttiilikokoa.

Tutkimuksissa paljastui useita reiän pienennyksiä hänen piirissään:

10mm syöttöjohto 8mm venttiilin aukkoihin (C₁ = 0,36).
8mm venttiilin portit 6mm liittimiin (C₂ = 0,44).
6 mm:n liittimet 8 mm:n sylinteriportteihin, joissa on sisäisiä rajoituksia (C₃ = 0,32).

Kokonaiskompensaatiokerroin oli Ctotal = 1 - (1-0,36)(1-0,44)(1-0,32) = 0,75, eli hänen järjestelmänsä menetti 75% teoreettisesta virtauskapasiteetistaan!

Parantamalla koko järjestelmää oikein mitoitetuilla komponenteilla poistimme nämä rajoitukset ja saavutimme vaaditun suorituskyvyn muuttamatta sylinteriä tai syöttöpaineita.

Käytännön strategiat reiän pienentämishäviöiden minimoimiseksi

Vähentää porauskatkoista aiheutuvia tappioita:

Komponenttien koko johdonmukaisesti koko paineilmapiirissä
Käytä suurinta käytännöllistä putkikokoa korkean virtauksen sovelluksiin
Kiinnitä huomiota sisäisten komponenttien rajoituksiin, ei vain liitäntäkoot
Tarkastellaan rinnakkaisia virtausreittejä suuren virtauksen vaatimuksia varten
Tarpeettomien sovittimien ja siirtymien eliminointi aina kun mahdollista

Pneumaattisten järjestelmien heikoin lenkki -periaate

Muista, että pneumaattisen järjestelmän suorituskykyä rajoittaa sen rajoittavin komponentti. Yksittäinen alimitoitettu elementti voi mitätöidä oikein mitoitettujen komponenttien hyödyt muualla järjestelmässä.

Esimerkiksi järjestelmä, jossa on 10 mm:n putket, 10 mm:n venttiilit mutta 6 mm:n liitokset sylinterissä, toimii olennaisesti samalla tavalla kuin järjestelmä, jossa on kauttaaltaan 6 mm:n komponentteja - mutta kalliimmalla.

Päätelmä

Virtausvastuksen ymmärtäminen ja oikeaoppinen laskeminen kitkakertoimitaulukoiden, ekvivalenttipituusmenetelmien ja pienennetyn läpiviennin kompensoinnin avulla on olennaista, jotta voidaan suunnitella pneumaattisia järjestelmiä, jotka toimivat odotetulla tavalla todellisissa olosuhteissa. Soveltamalla näitä laskentamenetelmiä ja suunnitteluperiaatteita voit optimoida sauvattomat sylinterisovellukset ja muut pneumaattiset järjestelmät mahdollisimman suorituskykyisiksi ja luotettaviksi.

Usein kysytyt kysymykset virtausvastuksesta pneumaattisissa järjestelmissä

Kuinka suuri painehäviö on hyväksyttävä pneumaattisessa järjestelmässä?

Hyväksyttävä painehäviö riippuu sovelluksen vaatimuksista, mutta yleisenä ohjeena on, että kokonaispainehäviö saa olla enintään 10-15% syöttöpaineesta tehokkaan toiminnan varmistamiseksi. 6 baarin järjestelmässä tämä tarkoittaa, että kokonaispainehäviö on alle 0,6-0,9 baaria. Kriittiset sovellukset saattavat vaatia vielä pienempiä painehäviöitä, 5-8%, tasaisen suorituskyvyn ylläpitämiseksi.

Mikä on putken halkaisijan ja painehäviön välinen suhde?

Painehäviö on kääntäen verrannollinen halkaisijan viidenteen potenssiin (D⁵) turbulenttisessa virtauksessa pneumaattisissa järjestelmissä. Tämä tarkoittaa, että putken halkaisijan kaksinkertaistaminen vähentää painehäviötä noin 32-kertaisesti. Esimerkiksi lisäämällä 6 mm:n putkesta 12 mm:n putkeen voidaan samoissa virtausolosuhteissa vähentää painehäviötä 1,5 baarista vain 0,047 baariin.

Miten määritän oikean putkikoon pneumaattiseen sovellukseeni?

Valitse putken koko virtausnopeusvaatimusten ja hyväksyttävän painehäviön perusteella. Laske Reynoldsin luku ja kitkakerroin ja määritä sitten Darcy-Weisbachin yhtälön avulla painehäviö eri halkaisijoille. Valitse pienin halkaisija, jolla painehäviö pysyy hyväksyttävissä rajoissa (yleensä <10% syöttöpaineesta), ottaen samalla huomioon tilarajoitukset ja kustannukset.

Kumpi aiheuttaa enemmän rajoituksia: 90° kulmakappale vai 5 metriä suoraa putkea?

Terävä 90° kulmakulma aiheuttaa tyypillisesti vastusta, joka vastaa 30 putken halkaisijan suoraa putkea. Jos kyseessä on 8 mm:n putki, yksi terävä kulmakappale vastaa noin 240 mm:n (30 × 8 mm) suoraa putkea. Tämä tarkoittaa, että 5 metriä suoraa putkea aiheuttaa noin 21 kertaa enemmän rajoituksia kuin yksi kulmakappale. Järjestelmissä on kuitenkin usein useita kulmakappaleita ja liittimiä, joiden kumulatiivinen vaikutus voi ylittää suoran putken pituuden häviöt.

Miten pikaliittimet vaikuttavat järjestelmän suorituskykyyn?

Tavalliset pikaliittimet aiheuttavat tyypillisesti paikallisen häviön, joka vastaa 15-25 putkihalkaisijaa suoraa putkea. Vielä merkittävämpää on, että monissa pikaliittimissä on nimelliskokoa pienemmät sisäiset rajoitukset. 10 mm:n pikaliittimessä saattaa olla vain 7-8 mm:n sisäinen rajoitus, jolloin läpivienti pienenee, mikä voi vähentää virtauskapasiteettia 50-70%:llä kyseisessä kohdassa.

Mikä on osittain suljettujen virtauksen säätöventtiilien vaikutus järjestelmän suorituskykyyn?

Virtauksensäätöventtiili, joka on suljettu 50%:n päähän täydestä läpimitasta, ei vähennä virtausta vain 50%:llä, vaan se vähentää virtausta noin 75%:llä, koska halkaisijan ja virtauskapasiteetin välinen suhde on epälineaarinen. Painehäviö kasvaa nopeuden muutoksen neliön mukaan, joten tehollisen halkaisijan puolittaminen kasvattaa painehäviötä noin 16-kertaiseksi samoissa virtausolosuhteissa.

Esittää yksityiskohtaisen erittelyn Darcy-Weisbachin yhtälöstä, joka on perustavanlaatuinen ja laajalti käytetty kaava nestedynamiikassa kitkasta johtuvan painehäviön laskemiseksi putkessa. ↩
Tarjoaa selkeän määritelmän Reynoldsin luvulle, joka on kriittinen dimensioton suure, jota käytetään virtaustapojen (laminaaristen tai turbulenttien) ennustamiseen erilaisissa nestevirtaustilanteissa. ↩
Esitetään Moody-diagrammi, kattava kaavio, jossa Darcy-kitkakerroin esitetään Reynoldsin lukua ja suhteellista karheutta vasten ja joka on insinöörien vakioväline painehäviön määrittämiseksi putkissa. ↩
Selitetään K-arvon eli paikallisen häviökertoimen käsite, joka on dimensioton luku, jota käytetään kuvaamaan painehäviötä putkiliitoksessa tai venttiilissä osana ekvivalenttipituusmenetelmää. ↩
Selostetaan yksityiskohtaisesti fysiikkaa, joka on taustalla painehäviön taustalla, kun neste kulkee rajoituksen (aukon) läpi, ja joka perustuu jatkuvuusyhtälön ja Bernoullin periaatteen periaatteisiin. ↩

Hei, olen Chuck, vanhempi asiantuntija, jolla on 15 vuoden kokemus pneumatiikka-alalta. Bepto Pneumaticilla keskityn tuottamaan asiakkaillemme laadukkaita, räätälöityjä pneumatiikkaratkaisuja. Asiantuntemukseni kattaa teollisuusautomaation, pneumatiikkajärjestelmien suunnittelun ja integroinnin sekä avainkomponenttien soveltamisen ja optimoinnin. Jos sinulla on kysyttävää tai haluat keskustella projektitarpeistasi, ota rohkeasti yhteyttä minuun osoitteessa chuck@bepto.com.