Siipityyppisten pyörivien toimilaitteiden fysiikkaan liittyy monimutkaisia vuorovaikutussuhteita nestedynamiikan, mekaanisten voimien ja termodynamiikan välillä, joita useimmat insinöörit eivät koskaan täysin ymmärrä. Näiden periaatteiden hallitseminen on kuitenkin ratkaisevan tärkeää suorituskyvyn optimoinnissa, käyttäytymisen ennustamisessa ja sellaisten sovellushaasteiden ratkaisemisessa, jotka voivat ratkaista projektin. 🔬
Siipityyppiset pyörivät toimilaitteet toimivat Pascalin paineen kerrannaisperiaatteella, joka muuntaa lineaarisen pneumaattisen voiman pyöriväksi vääntömomentiksi liukulapamekanismien avulla, ja niiden suorituskykyä säätelevät paine-erot, siipien geometria, kitkakertoimet ja termodynaamiset kaasulakiarvot, jotka määrittävät vääntömomentin tuoton, kierrosluvun ja hyötysuhteen ominaisuudet.
Työskentelin hiljattain Seattlessa sijaitsevassa ilmailu- ja avaruusteollisuuden tuotantolaitoksessa Jennifer-nimisen suunnitteluinsinöörin kanssa, joka kamppaili vääntömomentin epäjohdonmukaisuuksien kanssa pyörivän toimilaitteen sovelluksessa. Hänen toimilaitteensa tuottivat 30% laskettua vääntömomenttia vähemmän, mikä aiheutti paikannusvirheitä kriittisissä kokoonpanotoiminnoissa. Perimmäinen syy ei ollut mekaaninen, vaan perustavanlaatuinen väärinkäsitys siipitoimilaitteiden käyttäytymistä ohjaavasta fysiikasta. ✈️
Sisällysluettelo
- Miten paineen dynamiikka tuottaa pyörimismomentin venttiilityyppisissä toimilaitteissa?
- Mikä rooli siipien geometrialla on toimilaitteen suorituskykyominaisuuksien määrittämisessä?
- Mitkä termodynaamiset periaatteet vaikuttavat pyörivän toimilaitteen nopeuteen ja tehokkuuteen?
- Miten kitkavoimat ja mekaaniset häviöt vaikuttavat toimilaitteen suorituskykyyn todellisessa maailmassa?
Miten paineen dynamiikka tuottaa pyörimismomentin venttiilityyppisissä toimilaitteissa?
Paineen muuntaminen vääntömomentiksi on olennaisen tärkeää pyörivien toimilaitteiden suunnittelussa ja soveltamisessa.
Siipityyppiset toimilaitteet tuottavat vääntömomentin siipipintoihin vaikuttavien paine-erojen kautta, jolloin vääntömomentti on yhtä suuri kuin paine-ero kertaa siipien tehollinen pinta-ala kertaa momenttivarsi1 etäisyys suhteella T = ΔP × A × r, jota muutetaan siipikulman ja kammion geometrian mukaan, jotta lineaarisista pneumaattisista voimista saadaan aikaan pyörimisliike.
Vääntömomentin tuottamisen perusperiaatteet
Pascalin periaatteen soveltaminen
Pyörivän toimilaitteen toiminnan perusta on seuraavissa tekijöissä Pascalin periaate2:
- Paineen siirto: Tasainen paine vaikuttaa kaikkiin kammion sisäisiin pintoihin.
- Voimakertoimen kertolasku: Paine × pinta-ala = kuhunkin siipipintaan kohdistuva voima.
- Hetken luominen: Voima × säde = vääntömomentti keskiakselin ympäri.
Vääntömomentin laskennan perusteet
Vääntömomentin peruskaava: T = ΔP × A_eff × r_eff × η
Missä:
- T = Lähtömomentti (lb-in)
- ΔP = Paine-ero (PSI)
- A_eff = Tehollinen siipipinta-ala (neliömetriä).
- r_eff = Tehollinen momenttivarsi (tuumaa)
- η = mekaaninen hyötysuhde (0,85-0,95)
Paineen jakautumisen analyysi
Kammion paineen dynamiikka
Painejakauma siipikammioissa ei ole tasainen:
- Korkeapainekammio: Syöttöpaine miinus virtaushäviöt
- Matalapainekammio: Pakokaasupaine ja vastapaine
- Siirtymävyöhykkeet: Painegradientit siipien reunoilla
- Kuolleet volyymit: Ilman pysähtyminen välystiloihin
Tehollisen pinta-alan laskelmat
| Vane-konfiguraatio | Tehollisen pinta-alan kaava | Tehokkuuskerroin |
|---|---|---|
| Yksi tuulilasi | A = L × W × sin(θ) | 0.85-0.90 |
| Double Vane | A = 2 × L × W × sin(θ/2) | 0.88-0.93 |
| Multi-Vane | A = n × L × W × sin(θ/n) | 0.90-0.95 |
jossa L = siipien pituus, W = siipien leveys, θ = kiertokulma, n = siipien lukumäärä.
Dynaamisen paineen vaikutukset
Virtauksen aiheuttamat painehäviöt
Todellisen maailman painedynamiikkaan sisältyy virtaukseen liittyviä häviöitä:
- Sisääntulorajoitukset: Venttiilien ja liitosten painehäviöt
- Sisäiset virtaushäviöt: Turbulenssi ja kitka kammioissa
- Pakokaasurajoitukset: Pakojärjestelmien vastapaine
- Kiihtyvyyshäviöt: Liikkuvan ilman kiihdyttämiseen tarvittava paine
Jenniferin ilmailu- ja avaruussovellus kärsi riittämättömästä syöttölinjan mitoituksesta, joka aiheutti 15 PSI:n painehäviön toimilaitteen nopeiden liikkeiden aikana. Tämä painehäviö yhdessä dynaamisten virtausvaikutusten kanssa selitti 30%:n aiheuttaman vääntömomentin alenemisen. 📉
Mikä rooli siipien geometrialla on toimilaitteen suorituskykyominaisuuksien määrittämisessä?
Siipipyörän geometria vaikuttaa suoraan vääntömomenttiin, pyörimiskulmaan, nopeuteen ja hyötysuhdeominaisuuksiin.
Siipien geometria määrittää toimilaitteen suorituskyvyn siipien pituuden (vaikuttaa momenttivarteen), leveyden (määrittää painealueen), paksuuden (vaikuttaa tiivistykseen ja kitkaan), kulmasuhteiden (ohjaa pyörimisaluetta) ja välyksen määrittelyn (vaikuttaa vuotoon ja hyötysuhteeseen) kautta, ja jokainen parametri vaatii optimointia erityisiä sovelluksia varten.
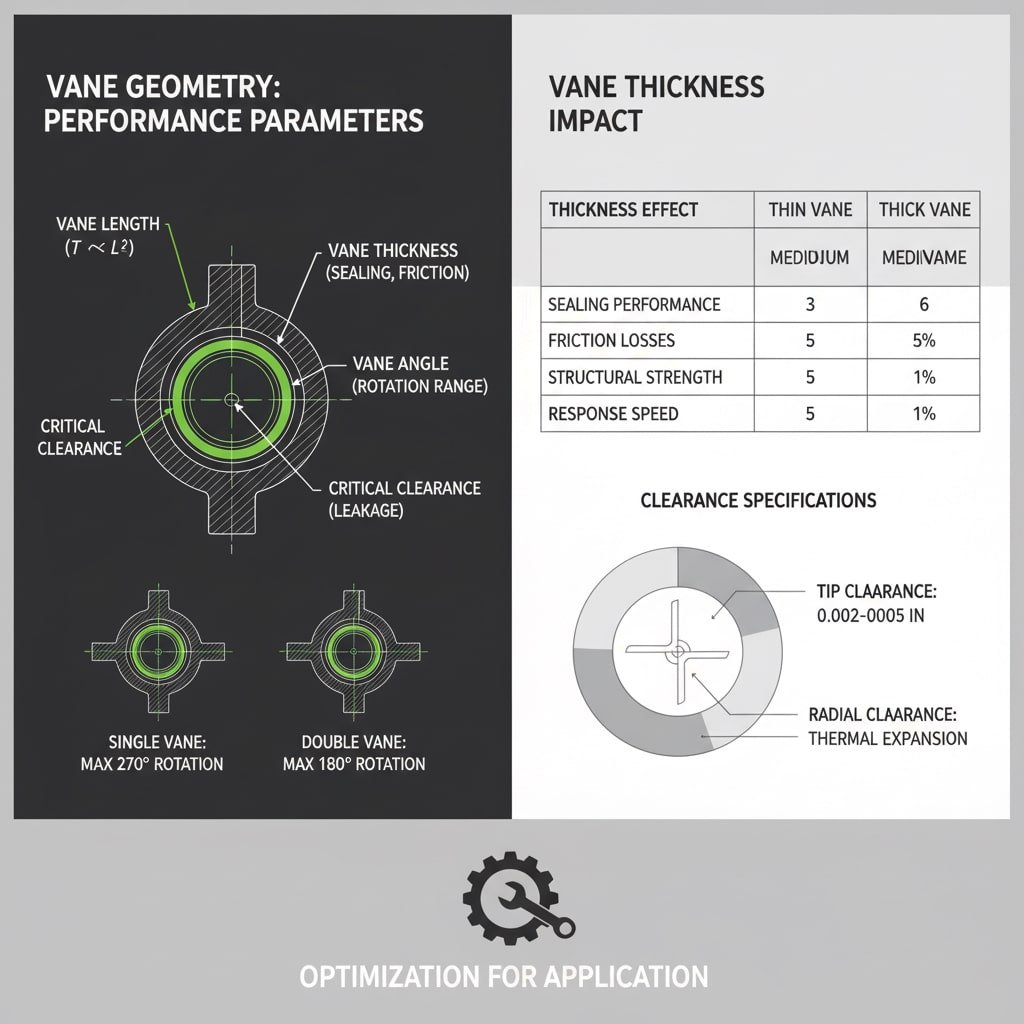
Geometristen parametrien analyysi
Siipipyörän pituuden optimointi
Siipipyörän pituus vaikuttaa suoraan vääntömomentin tuottoon ja rakenteelliseen eheyteen:
- Vääntömomenttisuhde: T ∝ L² (pituuden neliösuhde)
- Stressiä koskevat näkökohdat: Taivutusjännitys kasvaa pituuden kuutioidessa
- Poikkeusvaikutukset: Pidemmät siivet kokevat enemmän kärkipoikkeamaa.
- Optimaaliset suhteet: Pituuden ja leveyden suhde 3:1 - 5:1 takaa parhaan suorituskyvyn.
Ohjauslaipan paksuus Vaikutus
Siipipyörän paksuus vaikuttaa useisiin suorituskykyparametreihin:
| Paksuusvaikutus | Ohuet siivet (< 0,25″) | Keskikokoiset siivet (0.25″-0.5″) | Paksut siivet (> 0,5″) |
|---|---|---|---|
| Tiivistyksen suorituskyky | Huono - suuri vuoto | Hyvä - riittävä kontakti | Erinomainen - tiiviit tiivisteet |
| Kitkahäviöt | Matala | Medium | Korkea |
| Rakenteellinen lujuus | Huono - poikkeamaongelmat | Hyvä - riittävä jäykkyys | Erinomainen - jäykkä |
| Vastausnopeus | Nopea | Medium | Hidas |
Kulmageometriaan liittyvät näkökohdat
Kiertokulman rajoitukset
Siipipyörän geometria rajoittaa enimmäiskiertokulmia:
- Yksi siipi: Maksimi ~270° kierto
- Kaksoissiipi: Enimmäiskierto ~180°
- Monipyöräinen: Siipien häiriöt rajoittavat pyörimistä
- Kammion rakenne: Kotelon geometria vaikuttaa käyttökulmaan
Ohjauskulman optimointi
Siipien välinen kulma vaikuttaa vääntömomenttiominaisuuksiin:
- Yhtä suuri etäisyys: Tarjoaa tasaisen vääntömomentin luovutuksen
- Epätasainen väli: Voidaan optimoida vääntömomenttikäyrät tiettyjä sovelluksia varten.
- Progressiiviset kulmat: Painevaihtelujen kompensointi
Välys ja tiivistysgeometria
Kriittiset välyksen määrittelyt
Oikeat välykset tasapainottavat tiivisteen tehokkuutta ja kitkaa:
- Vihjeen tyhjennys: 0.002″-0.005″ optimaaliseen tiivistämiseen
- Sivuväli: 0,001″-0,003″ sitoutumisen estämiseksi
- Radiaalinen välys: Lämpötilan laajenemiseen liittyvät näkökohdat
- Aksiaalinen välys: Työntölaakeri ja lämpökasvu
Bepton siipien geometrian optimointiprosessissa käytetään seuraavia menetelmiä. laskennallinen nestedynamiikka (CFD)3 analyysi yhdistettynä empiiriseen testaukseen, jotta saadaan aikaan ihanteellinen vääntömomentin, nopeuden ja tehokkuuden tasapaino kuhunkin sovellukseen. Tämän teknisen lähestymistavan ansiosta olemme saavuttaneet 15-20% korkeamman hyötysuhteen kuin vakiomallit. 🔧
Mitkä termodynaamiset periaatteet vaikuttavat pyörivän toimilaitteen nopeuteen ja tehokkuuteen?
Termodynaamiset vaikutukset vaikuttavat merkittävästi toimilaitteen suorituskykyyn, erityisesti nopeissa tai suuritehoisissa sovelluksissa.
Pyöriviin toimilaitteisiin vaikuttavia termodynaamisia periaatteita ovat kaasun laajeneminen ja puristuminen pyörimisen aikana, kitkan ja painehäviöiden aiheuttama lämmöntuotanto, lämpötilan vaikutus ilman tiheyteen ja viskositeettiin sekä adiabaattiset ja isotermiset prosessit, jotka määrittävät todellisen ja teoreettisen suorituskyvyn todellisissa käyttöolosuhteissa.

Kaasulain sovellukset
Ideaalikaasun lain vaikutukset
Pyörivän toimilaitteen suorituskyky noudattaa kaasulakia:
- Paine-tilavuus-työ: W = ∫P dV laajentumisen aikana
- Lämpötilan vaikutukset: PV = nRT säätelee paineen ja lämpötilan välisiä suhteita.
- Tiheyden vaihtelut: ρ = PM/RT vaikuttaa massavirran laskentaan.
- Puristuvuus: Todelliset kaasuvaikutukset korkeissa paineissa
Adiabaattiset vs. isotermiset prosessit
Toimilaitteen toimintaan liittyy molempia prosessityyppejä:
| Prosessin tyyppi | Ominaisuudet | Suorituskyvyn vaikutus |
|---|---|---|
| Adiabaattinen | Ei lämmönsiirtoa, nopea laajeneminen | Suuremmat painehäviöt, lämpötilan muutokset |
| Isoterminen | Jatkuva lämpötila, hidas laajeneminen | Tehokkaampi energian muuntaminen |
| Polytrooppinen | Todellisen maailman yhdistelmä | Todellinen suorituskyky ääriarvojen välillä |
Lämmöntuotanto ja -siirto
Kitkan aiheuttama lämmitys
Pyörivissä toimilaitteissa syntyy lämpöä useista eri lähteistä:
- Kiekon kärjen kitka: Liukukosketus kotelon kanssa
- Laakerikitka: Akselin tukilaakerin häviöt
- Tiivisteen kitka: Pyörivän tiivisteen vetovoimat
- Nesteen kitka: Viskoosihäviöt ilmavirtauksessa
Lämpötilan nousun laskelmat
Lämmöntuotantoaste: Q = μ × N × F × V
Missä:
- Q = Lämmöntuotanto (BTU/h)
- μ = kitkakerroin
- N = pyörimisnopeus (RPM)
- F = Normaalivoima (lbs)
- V = Liukunopeus (ft/min)
Tehokkuusanalyysi
Termodynaamiset tehokkuustekijät
Kokonaishyötysuhde yhdistää useita häviömekanismeja:
- Tilavuushyötysuhde: ηv = Todellinen virtaus / Teoreettinen virtaus
- Mekaaninen tehokkuus: ηm = lähtöteho / tuloteho
- Kokonaishyötysuhde: ηo = ηv × ηm
Tehokkuuden optimointistrategiat
| Strategia | Tehokkuuden kasvu | Toteutuskustannukset |
|---|---|---|
| Parannettu tiivistys | 5-15% | Medium |
| Optimoidut välykset | 3-8% | Matala |
| Kehittyneet materiaalit | 8-12% | Korkea |
| Lämmönhallinta | 5-10% | Medium |
Virtausdynamiikka ja painehäviöt
Reynoldsin luvun vaikutukset
Virtausominaisuudet muuttuvat käyttöolosuhteiden mukaan:
- Laminaarinen virtaus: Re < 2300, ennakoitavat painehäviöt
- Turbulenttinen virtaus: Re > 4000, korkeammat kitkakertoimet
- Siirtymäalue: Ennustamattomat virtausominaisuudet
Termodynaaminen analyysi osoitti, että Jenniferin ilmailu- ja avaruussovelluksen lämpötila nousi merkittävästi nopean syklityksen aikana, mikä vähensi ilman tiheyttä 12% ja vaikutti vääntömomentin menetykseen. Toteutimme lämmönhallintastrategioita, jotka palauttivat täyden suorituskyvyn. 🌡️
Miten kitkavoimat ja mekaaniset häviöt vaikuttavat toimilaitteen suorituskykyyn todellisessa maailmassa?
Kitka ja mekaaniset häviöt vähentävät teoreettista suorituskykyä merkittävästi, ja niitä on hallittava huolellisesti, jotta toimilaite toimisi optimaalisesti.
Siipityyppisten toimilaitteiden mekaanisiin häviöihin kuuluvat liukukitka siipien kärjissä, pyörivän tiivisteen vastus, laakerikitka ja sisäinen ilmaturbulenssi, jotka tyypillisesti pienentävät teoreettista vääntömomenttia 10-20% ja edellyttävät huolellista materiaalivalintaa, pintakäsittelyä ja voitelustrategioita suorituskyvyn heikkenemisen minimoimiseksi.
Kitka-analyysi ja mallinnus
Kitkamekanismit
Ensisijainen kitkalähde on pakettiauton ja kotelon rajapinnoissa:
- Rajavoitelu: Suora metalli-metalli-kosketus
- Sekavoitelu: Osittainen nestekalvon erottaminen
- Hydrodynaaminen voitelu: Täysi nestekalvo (harvinainen pneumatiikassa)
Kitkakertoimen vaihtelut
| Materiaaliyhdistelmä | Kuivakitka (μ) | Voitelukitka (μ) | Lämpötilaherkkyys |
|---|---|---|---|
| Terästä terästä vastaan | 0.6-0.8 | 0.1-0.15 | Korkea |
| Terästä pronssille | 0.3-0.5 | 0.08-0.12 | Medium |
| Teräs PTFE:llä | 0.1-0.2 | 0.05-0.08 | Matala |
| Keraaminen pinnoite | 0.2-0.3 | 0.06-0.10 | Erittäin alhainen |
Laakerihäviöanalyysi
Radiaalilaakerin kitka
Lähtöakselin laakerit aiheuttavat merkittäviä häviöitä:
- Vierintäkitka: Fr = μr × N × r
- Liukukitka: Fs = μs × N
- Viskoosinen kitka: Fv = η × A × V/h
- Tiivisteen kitka: Akselitiivisteiden aiheuttama lisävastus
Laakerin valinnan vaikutus
Eri laakerityypit vaikuttavat kokonaistehokkuuteen:
- Kuulalaakerit: Alhainen kitka, korkea tarkkuus
- Rullalaakerit: Suurempi kantavuus, kohtalainen kitka
- Liukulaakerit: Korkea kitka, yksinkertainen rakenne
- Magneettilaakerit: Lähes nolla kitkaa, korkeat kustannukset
Pintatekniset ratkaisut
Kehittyneet pintakäsittelyt
Nykyaikaiset pintakäsittelyt vähentävät kitkaa huomattavasti:
- Kovakromaus: Vähentää kulumista, kohtalainen kitkan vähennys
- Keraamiset pinnoitteet: Erinomainen kulutuskestävyys, alhainen kitka
- Timantin kaltainen hiili (DLC): Erittäin matala kitka, kallis
- Erikoispolymeerit: Sovelluskohtaiset ratkaisut
Voitelustrategiat
| Voitelumenetelmä | Kitkan vähentäminen | Huoltovaatimukset | Kustannusvaikutus |
|---|---|---|---|
| Öljysumujärjestelmät | 60-80% | Korkea - säännöllinen täydennys | Korkea |
| Kiinteät voiteluaineet | 40-60% | Alhainen - pitkä käyttöikä | Medium |
| Itsevoitelevat materiaalit | 50-70% | Erittäin alhainen - pysyvä | Korkea alkuperäinen |
| Kuivakalvon voiteluaineet | 30-50% | Keskisuuri - säännöllinen uudelleenlevitys | Matala |
Suorituskyvyn optimointistrategiat
Integroitu suunnittelutapa
Beptossa optimoimme kitkan järjestelmällisen suunnittelun avulla:
- Materiaalin valinta: Yhteensopivat materiaaliparit
- Pintakäsittely: Optimoitu karheus kutakin sovellusta varten
- Tyhjentämisen valvonta: Minimoi kosketuspaine
- Lämmönhallinta: Lämpötilan aiheuttaman laajenemisen hallinta
Suorituskyvyn validointi todellisessa maailmassa
Laboratoriotestit ja kenttäkokeet eroavat usein toisistaan:
- Sisäänajovaikutukset: Suorituskyky paranee ensimmäisellä käyttökerralla
- Saastumisen vaikutus: Todellisen maailman lika- ja roskatehosteet
- Lämpötilan vaihtelu: Lämpölaajeneminen ja supistuminen
- Kuormituksen vaihtelut: Dynaaminen kuormitus verrattuna staattisiin testiolosuhteisiin
Kattava kitka-analyysi- ja optimointiohjelmamme auttoi Jenniferin ilmailu- ja avaruussovellusta saavuttamaan 95%:n teoreettisen vääntömomentin, mikä on merkittävä parannus alkuperäiseen 70%:hen verrattuna. Avain oli monitahoisen lähestymistavan toteuttaminen, jossa yhdistyvät edistykselliset materiaalit, optimoitu geometria ja asianmukainen voitelu. 🎯
Ennakoiva kitkamallinnus
Matemaattiset kitkamallit
Tarkka kitkan ennustaminen edellyttää kehittynyttä mallintamista:
- Coulombin kitka: F = μ × N (perusmalli)
- Stribeckin käyrä: Kitkan vaihtelu nopeuden mukaan
- Lämpötilan vaikutukset: μ(T) suhteet
- Kulumisen eteneminen: Kitka muuttuu ajan myötä
Päätelmä
Siipityyppisten pyörivien toimilaitteiden perusfysiikan ymmärtäminen - paineen dynamiikasta ja termodynamiikasta kitkamekanismeihin - antaa insinööreille mahdollisuuden optimoida suorituskykyä, ennustaa käyttäytymistä ja ratkaista monimutkaisia sovellushaasteita.
Usein kysytyt kysymykset Vane-tyyppisen pyörivän toimilaitteen fysiikasta
K: Miten käyttöpaine vaikuttaa teoreettisen ja todellisen vääntömomentin väliseen suhteeseen?
V: Suuremmat käyttöpaineet parantavat yleensä teoreettista ja todellista vääntömomenttisuhdetta, koska mekaaniset häviöt ovat pienempi prosenttiosuus kokonaistuotosta. Suurempi paine lisää kuitenkin myös kitkavoimia, joten suhde ei ole lineaarinen. Optimaalinen paine riippuu sovelluksen erityisvaatimuksista ja toimilaitteen suunnittelusta.
K: Miksi pyörivät toimilaitteet menettävät vääntömomenttia suurilla nopeuksilla ja miten tämä voidaan minimoida?
V: Suurten nopeuksien vääntömomentin menetys johtuu lisääntyneestä kitkasta, virtausrajoituksista ja termodynaamisista vaikutuksista. Minimoi häviöt optimoidulla aukkojen mitoituksella, kehittyneillä laakerijärjestelmillä, paremmilla tiivistysmalleilla ja lämmönhallinnalla. Virtausnopeusrajoituksista tulee ensisijainen rajoitus tiettyjen nopeuksien yläpuolella.
Kysymys: Miten lämpötilan vaihtelut vaikuttavat pyörivän toimilaitteen suorituskyvyn laskelmiin?
V: Lämpötila vaikuttaa ilman tiheyteen (vaikuttaa voimaan), viskositeettiin (vaikuttaa virtaukseen), materiaalin ominaisuuksiin (muuttaa kitkaa) ja lämpölaajenemiseen (muuttaa välyksiä). Lämpötilan nousu 100 °F voi vähentää vääntömomenttia 15-25%:llä yhdistettyjen vaikutusten vuoksi. Ohjausjärjestelmien lämpötilakompensointi auttaa ylläpitämään tasaista suorituskykyä.
K: Mikä on siipien kärkinopeuden ja kitkahäviöiden välinen suhde pyörivissä toimilaitteissa?
V: Kitkahäviöt kasvavat yleensä kärjen nopeuden neliön myötä, mikä johtuu lisääntyneistä kosketusvoimista ja lämmöntuotannosta. Hyvin alhaisilla nopeuksilla staattinen kitka on kuitenkin hallitseva, mikä luo monimutkaisen suhteen. Optimaaliset käyttönopeudet sijoittuvat yleensä keskialueelle, jossa dynaaminen kitka on hallittavissa.
Kysymys: Miten ilman kokoonpuristuvuus otetaan huomioon pyörivien toimilaitteiden suorituskykylaskelmissa?
V: Ilman kokoonpuristuvuus muuttuu merkittäväksi yli 100 PSI:n paineissa ja nopean kiihdytyksen aikana. Käytä kokoonpuristuvia virtausyhtälöitä kokoonpuristumattomuusoletusten sijasta, ota huomioon paineaaltojen etenemisviiveet ja ota huomioon adiabaattiset laajenemisvaikutukset. Todellisia kaasun ominaisuuksia saatetaan tarvita yli 200 PSI:n korkeapainesovelluksissa.
-
Opettele momenttivarren määritelmä, joka on kohtisuorassa oleva etäisyys pyörimisakselista voiman vaikutussuuntaan, mikä on ratkaisevan tärkeää vääntömomentin laskennassa. ↩
-
Ymmärrä Pascalin periaate, nestemekaniikan peruslaki, joka selittää, miten paine siirtyy suljetussa nesteessä. ↩
-
Tutustu laskennalliseen nestedynamiikkaan (CFD), joka on nestemekaniikan osa-alue, jossa käytetään numeerista analyysia nestevirtoihin liittyvien ongelmien ratkaisemiseen ja analysointiin. ↩




