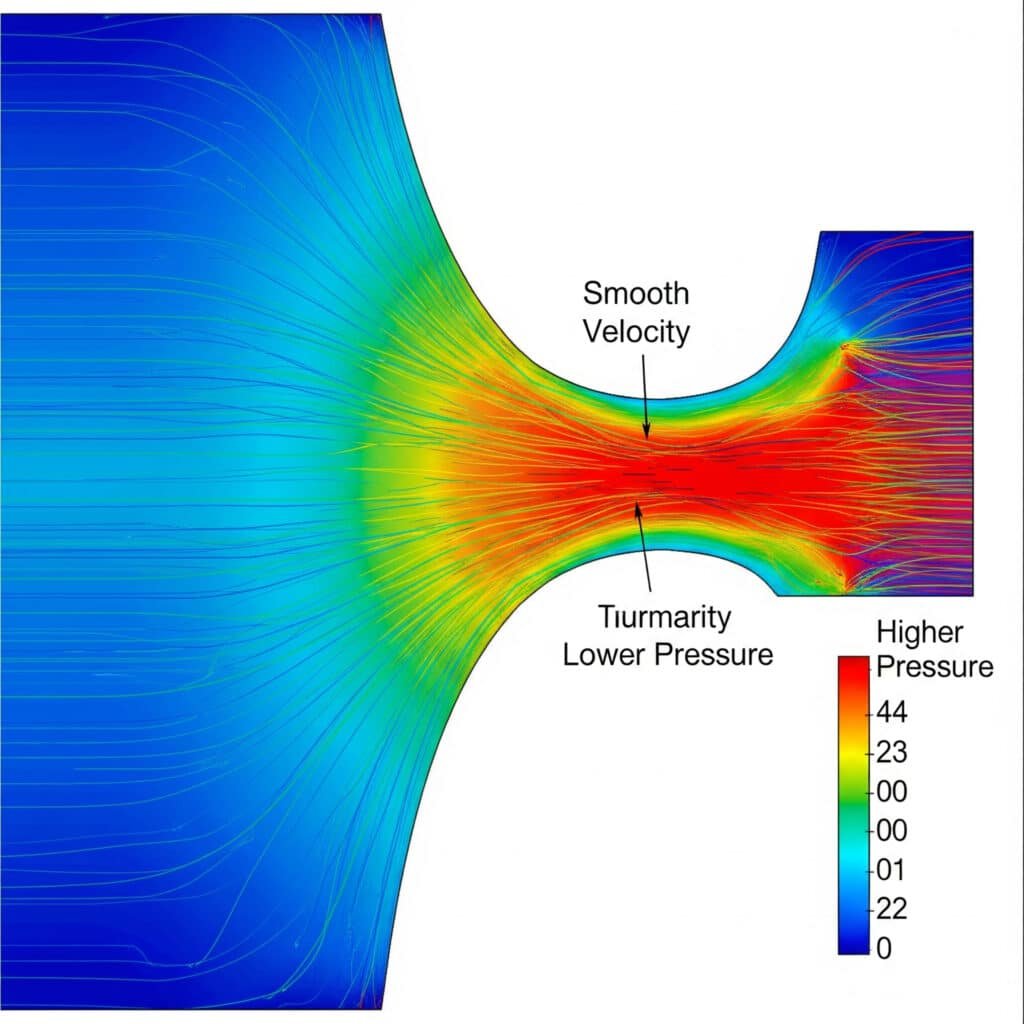
A gázáramlási problémák évente milliárdokba kerülnek a gyártóknak energiapazarlás és rendszerhibák miatt. A mérnökök gyakran folyadékáramlási elveket alkalmaznak gázrendszerekre, ami katasztrofális téves számításokhoz vezet. A gázáramlási elvek megértése megelőzi a költséges tervezési hibákat és a biztonsági kockázatokat.
A gázáramlás elvét a folytonossági egyenlet, az impulzusmegőrzés és az energia megőrzése szabályozza, ahol a gáz sebessége, nyomása, sűrűsége és hőmérséklete kölcsönhatásban van egymással. kompresszibilis áramlás1 az összenyomhatatlan folyadékáramlástól alapvetően eltérő egyenletek.
Két évvel ezelőtt egy Sarah Thompson nevű brit vegyészmérnökkel dolgoztam együtt, akinek a földgázelosztó rendszerében veszélyes nyomásingadozások voltak. A csapata összenyomhatatlan áramlási számításokat használt összenyomható gázáramlásra. A megfelelő gázáramlási elvek bevezetése után megszüntettük a nyomásingadozásokat, és 35%-vel csökkentettük az energiafogyasztást.
Tartalomjegyzék
- Melyek a gázáramlás alapelvei?
- Miben különböznek a kompresszibilis áramlási egyenletek a folyadékáramlástól?
- Milyen tényezők befolyásolják a gázáramlás viselkedését az ipari rendszerekben?
- Hogyan hat egymásra a nyomás, a hőmérséklet és a sebesség a gázáramlásban?
- Melyek a különböző típusú gázáramlási rendszerek?
- Hogyan számítsuk ki és optimalizáljuk a gázáramlást ipari alkalmazásokban?
- Következtetés
- GYIK a gázáramlási elvekről
Melyek a gázáramlás alapelvei?
A gázáramlás három alapvető megőrzési törvény szerint működik, amelyek minden folyadék mozgását szabályozzák, de a gáz összenyomhatósága és a sűrűségváltozások miatt egyedi jellemzőkkel bírnak.
A gázáramlás alapelvei a tömegmegmaradáson (folytonossági egyenlet), az impulzusmegmaradáson (Newton második törvénye) és az energia megmaradásán (a termodinamika első törvénye) alapulnak, a kompresszibilis folyadékok viselkedésére módosított formában.
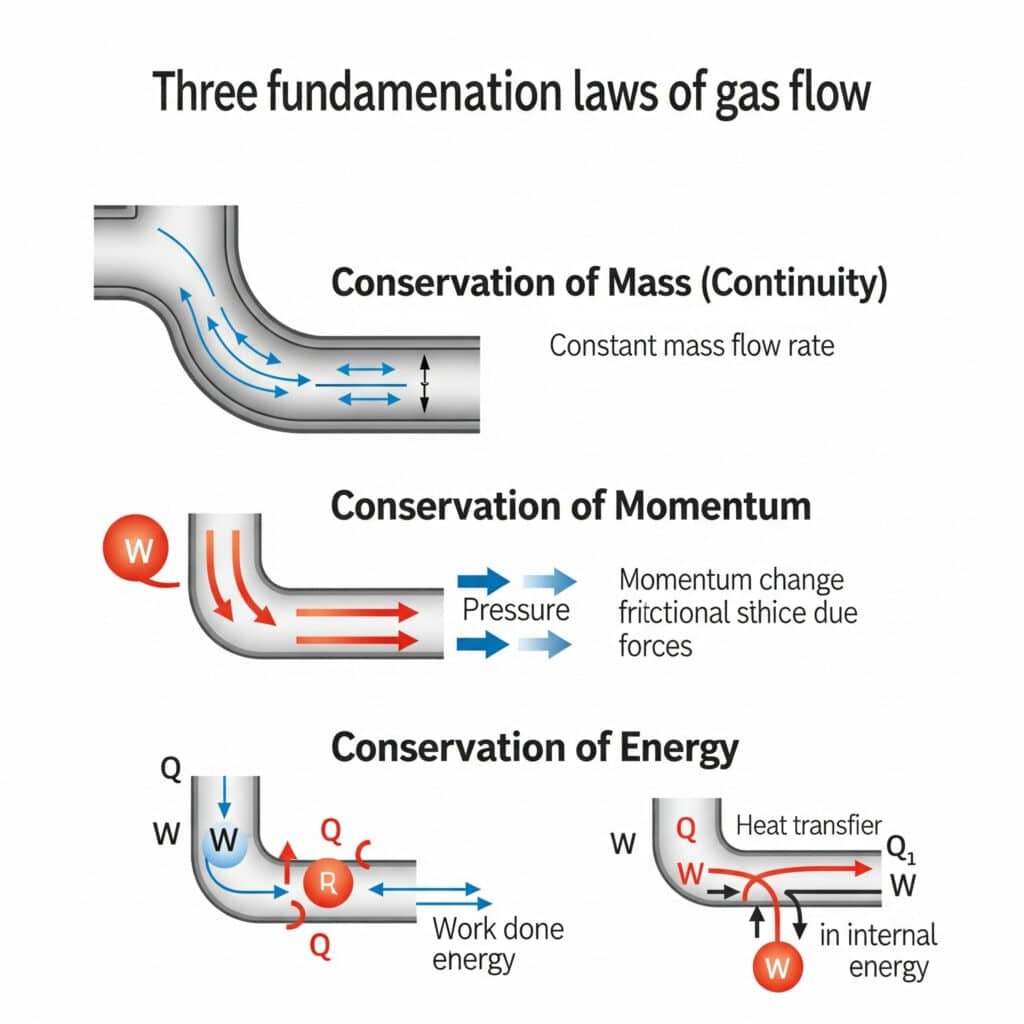
Tömegmegmegmaradás (folytonossági egyenlet)
A gázáramlás folytonossági egyenlete figyelembe veszi a nyomás- és hőmérsékletváltozások miatt bekövetkező sűrűségváltozásokat, ellentétben az összenyomhatatlan folyadékokkal.
Gázáramlási folytonossági egyenlet:
∂ρ/∂t + ∇-(ρV) = 0
Folyamatos áramláshoz: ρ₁A₁V₁ = ρ₂A₂V₂
Hol:
- ρ = Gáz sűrűsége (a nyomástól és a hőmérséklettől függően változik)
- A = Keresztmetszeti terület
- V = gázsebesség
- t = idő
Legfontosabb következmények:
- A gáz sűrűsége a nyomás és a hőmérséklet függvényében változik
- A tömegáram állandó áramlás esetén állandó marad
- A sűrűség csökkenésével nő a sebesség
- A területváltozások mind a sebességet, mind a sűrűséget befolyásolják
A lendület megőrzése
A gázáramlásban a nyomatékmegőrzés figyelembe veszi az összenyomható folyadékra ható nyomóerőket, viszkózus erőket és testerőket.
Lendület egyenlet (Navier-Stokes2):
ρ(∂V/∂t + V-∇V) = -∇p + μ∇²V + ρg
Gázáramú alkalmazásokhoz:
- A nyomásgradiens kifejezés dominál a nagy sebességű áramlásban
- A falak közelében és lamináris áramlásban fontos viszkózus hatások
- A kompresszibilitási hatások 0,3 Mach felett válnak jelentőssé.
Az energia megőrzése
A gázáramlás energiamegőrzése magában foglalja a kinetikus energiát, a potenciális energiát, a belső energiát és az áramlási munkát, figyelembe véve a tömörítés és tágulás miatti hőmérsékletváltozást.
Energiaegyenlet:
h + V²/2 + gz = állandó (az áramvonal mentén)
Hol:
- h = fajlagos entalpia (tartalmazza a belső energiát és az áramlási munkát)
- V²/2 = Kinetikus energia egységnyi tömegre vetítve
- gz = Tömegegységre jutó potenciális energia
Energetikai megfontolások:
| Energia forma | Gázáramlás hatása | Tipikus nagyságrend |
|---|---|---|
| Kinetikus energia | Nagy sebességeknél jelentős | V²/2 |
| Nyomás Energia | A legtöbb alkalmazásban domináns | p/ρ |
| Belső energia | Változások a hőmérséklet függvényében | CᵥT |
| Flow munka | Gázmozgáshoz szükséges | pv |
Állapotegyenlet
A gázáramláshoz a nyomás, a sűrűség és a hőmérséklet összefüggésbe hozásához állapotegyenletre van szükség, amely a legtöbb ipari alkalmazásban jellemzően az ideális gáztörvény.
Ideális gáztörvény:
p = ρRT
Hol:
- p = abszolút nyomás
- ρ = Gáz sűrűsége
- R = fajlagos gázállandó
- T = abszolút hőmérséklet
Valódi gázok esetében bonyolultabb állapotegyenletekre lehet szükség, például van der Waals- vagy Redlich-Kwong-egyenletekre.
Miben különböznek a kompresszibilis áramlási egyenletek a folyadékáramlástól?
A kompresszibilis gázáramlás alapvetően másképp viselkedik, mint az inkompresszibilis folyadékáramlás, ami speciális elemzési módszereket és tervezési megfontolásokat igényel.
A kompresszibilis áramlás a sűrűségváltozások, a hangsebesség-korlátozások, a lökéshullámok kialakulása és a hőmérséklet-nyomás csatolás révén különbözik, ami az inkompresszibilis folyadékáramlási rendszerekben nem fordul elő.
Sűrűségváltozási hatások
A gáz sűrűsége jelentősen változik a nyomás és a hőmérséklet függvényében, ami befolyásolja az áramlási mintázatot, a sebességeloszlást és a rendszer tervezési követelményeit.
Sűrűségváltozás hatásai:
- Sebesség Gyorsulás: A gáz tágulás közben felgyorsul
- Nyomáscsökkenés: Nem lineáris nyomás-áramlási kapcsolatok
- Hőmérsékleti hatások: A sűrűség fordítottan arányos a hőmérséklettel
- Fojtott áramlás: Maximális áramlási korlátozások
Hangsebesség és Mach-szám
A gázok áramlási viselkedése drámaian megváltozik, ahogy a sebesség megközelíti a hangsebességet, ami olyan kritikus tervezési korlátokat hoz létre, amelyek a folyékony rendszereknél nincsenek jelen.
Szonikus sebesség számítása:
a = √(γRT)
Hol:
- a = hangsebesség gázban
- γ = fajhőhányados (Cp/Cv)
- R = fajlagos gázállandó
- T = abszolút hőmérséklet
Mach-szám3 Jelentősége:
M = V/a (A sebesség aránya a hangsebességhez képest)
| Mach tartomány | Áramlási rendszer | Jellemzők |
|---|---|---|
| M < 0.3 | Összenyomhatatlan | Sűrűség lényegében állandó |
| 0.3 < M < 1.0 | Szubszonikus Összenyomható | Jelentős sűrűségváltozások |
| M = 1.0 | Sonic | Kritikus áramlási feltételek |
| M > 1.0 | Szuperszonikus | Lökéshullámok lehetségesek |
Fojtott áramlási jelenség
Fojtott áramlás4 akkor következik be, amikor a gázsebesség eléri a szonikus feltételeket, ami a maximális áramlási sebességet korlátozza, függetlenül a nyomáscsökkentéstől.
Fojtott áramlási feltételek:
- Maximális elért tömegáram
- A lefelé irányuló nyomásváltozások nem befolyásolják a felfelé irányuló áramlást.
- Kritikus nyomásarány: p₂/p₁ ≈ 0,53 levegő esetében.
- Fúvókákban, nyílásokban és vezérlőszelepekben gyakori.
Hőmérséklet-nyomás csatolás
A gázáramlás a tágulás és a tömörítés miatt jelentős hőmérsékletváltozásokkal jár, ami hatással van a rendszer teljesítményére és kialakítására.
Termodinamikai folyamatok:
- Izentróp áramlás: Megfordítható, adiabatikus folyamat
- Izotermikus áramlás: Állandó hőmérséklet (lassú áramlás hőátadással)
- Adiabatikus áramlás: Nincs hőátadás (gyors áramlás)
- Polytróp áramlás: Általános eset hőátadással
Milyen tényezők befolyásolják a gázáramlás viselkedését az ipari rendszerekben?
Az ipari alkalmazásokban a gázáramlás viselkedését több tényező befolyásolja, így a rendszer megfelelő tervezéséhez és üzemeltetéséhez átfogó elemzésre van szükség.
A legfontosabb tényezők közé tartoznak a gáz tulajdonságai, a rendszer geometriája, az üzemi körülmények, a hőátadási hatások és a falsúrlódás, amelyek együttesen határozzák meg az áramlási mintázatot, a nyomásesést és a rendszer teljesítményét.
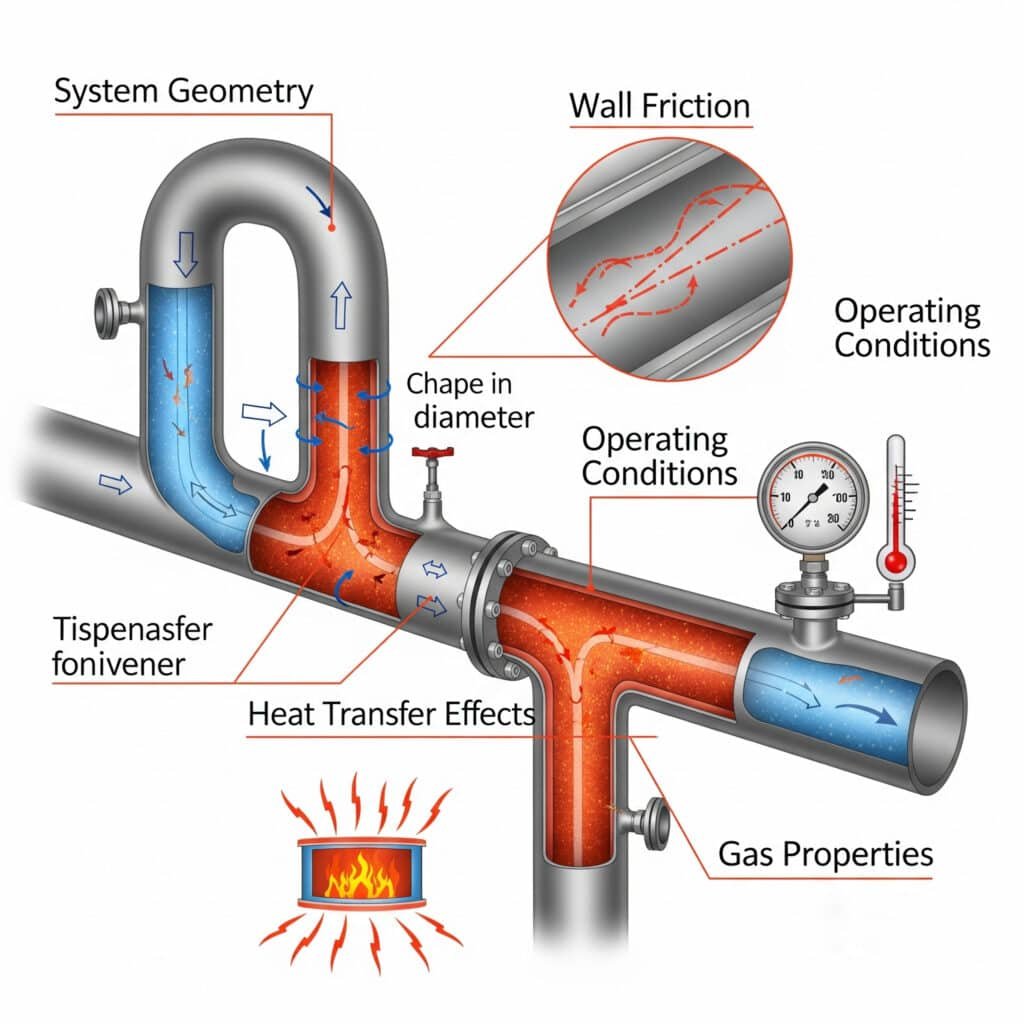
Gáz tulajdonságai Hatás
A különböző gázok molekuláris tulajdonságaik, fajhő arányuk és termodinamikai viselkedésük alapján eltérő áramlási jellemzőkkel rendelkeznek.
Kritikus gáztulajdonságok:
| Ingatlan | Szimbólum | Az áramlásra gyakorolt hatás | Tipikus értékek |
|---|---|---|---|
| Fajlagos hőarány | γ | Hangsebesség, tágulás | 1,4 (levegő), 1,3 (CO₂) |
| Gázkonstans | R | Sűrűség-nyomás kapcsolat | 287 J/kg-K (levegő) |
| Viszkozitás | μ | Súrlódási veszteségek | 1,8×10-⁵ Pa-s (levegő) |
| Molekulatömeg | M | Sűrűség adott körülmények között | 29 kg/kmol (levegő) |
Rendszergeometria hatásai
A csövek átmérője, hossza, szerelvények és az áramlási terület változásai jelentősen befolyásolják a gázáramlási mintázatot és a nyomásveszteségeket.
Geometriai megfontolások:
- Cső átmérője: Befolyásolja a sebességet és a súrlódási veszteségeket.
- Hosszúság: Meghatározza a teljes súrlódási nyomásesést
- Területi változások: Gyorsítási/lassítási hatások létrehozása
- Szerelvények: Helyi nyomásveszteséget okoz
- Felületi érdesség: Befolyásolja a súrlódási tényezőt
Üzemi nyomás és hőmérséklet
A rendszer működési feltételei a termodinamikai összefüggéseken keresztül közvetlenül befolyásolják a gáz sűrűségét, viszkozitását és áramlási viselkedését.
Üzemi állapot hatásai:
- Nagy nyomás: Növeli a sűrűséget, csökkenti a tömöríthetőségi hatásokat
- Alacsony nyomás: Csökkenti a sűrűséget, növeli a sebességet
- Magas hőmérséklet: Csökkenti a sűrűséget, növeli a hangsebességet.
- Alacsony hőmérséklet: Növeli a sűrűséget, kondenzációt okozhat
Hőátviteli hatások
A gázáramlás során a hő hozzáadása vagy eltávolítása jelentősen befolyásolja a hőmérséklet, a sűrűség és a nyomás eloszlását.
Hőátadási forgatókönyvek:
- Fűtés: Növeli a hőmérsékletet, csökkenti a sűrűséget, gyorsítja az áramlást.
- Hűtés: Csökkenti a hőmérsékletet, növeli a sűrűséget, lassítja az áramlást.
- Adiabatikus: Nincs hőátadás, hőmérsékletváltozás a tágulás/tömörödés miatt.
- Izotermikus: Állandó hőmérséklet fenntartása hőátadással
Fal súrlódási hatás
A gáz és a csőfalak közötti súrlódás nyomásveszteséget okoz és befolyásolja a sebességprofilokat, ami különösen fontos a hosszú csővezetékek esetében.
Súrlódási veszteség számítása:
Δp = f × (L/D) × (ρV²/2)
Hol:
- f = súrlódási tényező (a Reynolds-szám és az érdesség függvénye)
- L = A cső hossza
- D = csőátmérő
- ρ = Gáz sűrűsége
- V = gázsebesség
Hogyan hat egymásra a nyomás, a hőmérséklet és a sebesség a gázáramlásban?
A gázáramlásban a nyomás, a hőmérséklet és a sebesség közötti kölcsönhatás összetett összefüggéseket hoz létre, amelyeket a megfelelő rendszertervezéshez és elemzéshez meg kell érteni.
A gázáramlási kölcsönhatások termodinamikai összefüggéseket követnek, ahol a nyomásváltozások a hőmérsékletet és a sűrűséget, a sebességváltozások a nyomást az impulzushatásokon keresztül, a hőmérsékletváltozások pedig az összes többi tulajdonságot az állapotegyenleten keresztül befolyásolják.
Nyomás-sebesség összefüggések
A gázsebesség és a nyomás fordítottan függ össze a Bernoulli-egyenleten keresztül, amely a kompresszibilis áramlásra módosul, ami egyedi tervezési kihívásokat teremt.
Módosított Bernoulli-egyenlet gázáramlásra:
∫dp/ρ + V²/2 + gz = állandó
Ideális gáz esetén: γ/(γ-1) × (p/ρ) + V²/2 = állandó
Nyomás-sebesség hatások:
- Nyomáscsökkenés: A gáz tágulása miatt sebességnövekedést okoz.
- Sebességnövekedés: A lendülethatás miatt további nyomásesést okozhat
- Gyorsítás: Természetes módon keletkezik, ahogy a gáz kitágul a rendszeren keresztül
- Lassítás: Nyomásnövekedést vagy területbővítést igényel
Hőmérséklet-sebesség kapcsolat
A gáz hőmérséklete és sebessége az energiamegőrzés révén összekapcsolódik, a hőmérsékletváltozás pedig befolyásolja a gáz tulajdonságait és áramlási viselkedését.
Hőmérséklet-sebesség összefüggések:
T₀ = T + V²/(2Cp)
Hol:
- T₀ = stagnálási (teljes) hőmérséklet
- T = statikus hőmérséklet
- V = gázsebesség
- Cp = fajhő állandó nyomáson
Gyakorlati következmények:
- A nagy sebességű gázáramlás csökkenti a statikus hőmérsékletet
- Adiabatikus áramlás esetén a stagnálási hőmérséklet állandó marad.
- A hőmérséklet-változások befolyásolják a gáz sűrűségét és viszkozitását
- A hűtés egyes gázoknál kondenzációt okozhat.
Nyomás-hőmérséklet hatások
A nyomás és a hőmérséklet az állapotegyenleten és a termodinamikai folyamatokon keresztül kölcsönhatásba lép, és befolyásolja a gáz sűrűségét és áramlási jellemzőit.
Termodinamikai folyamatok összefüggései:
| Folyamat típusa | Nyomás-hőmérséklet összefüggés | Alkalmazás |
|---|---|---|
| Izentropikus | p/p₀ = (T/T₀)^(γ/(γ-1)) | Fúvókák, diffúzorok |
| Izotermikus | pV = állandó, T = állandó | Lassú áramlás hőátadással |
| Izobárikus | p = állandó | Állandó nyomású fűtés |
| Isochoric | V = állandó | Állandó térfogatú fűtés |
Sűrűségváltozások
A gáz sűrűsége az ideális gáztörvény szerint változik a nyomás és a hőmérséklet függvényében, ami összetett áramlási viselkedést eredményez.
Sűrűségszámítás:
ρ = p/(RT)
Sűrűség hatása az áramlásra:
- Nagy sűrűségű: Alacsonyabb sebesség adott tömegáram esetén
- Alacsony sűrűség: Nagyobb sebesség, lehetséges összenyomhatósági hatások
- Sűrűség gradiensek: Felhajtóerő és keveredési effektusok létrehozása
- Sűrűség változások: Hatással van a lendület- és energiaátvitelre
Nemrégiben segítettem egy Robert Chen nevű amerikai földgázmérnöknek Texasban a csővezetékrendszerének optimalizálásában. A hőmérséklet-nyomás-sebesség kölcsönhatások megfelelő figyelembevételével 28%-tal csökkentettük a szivattyúzási energiát, miközben 15%-tal növeltük az átbocsátási kapacitást.
Melyek a különböző típusú gázáramlási rendszerek?
A gázáramlás a sebesség, a nyomásviszonyok és a rendszer geometriája alapján különböző rendszereket mutat, amelyek mindegyike speciális elemzési módszereket és tervezési megfontolásokat igényel.
A gázáramlási rendszerek közé tartozik a lamináris, turbulens, szubszonikus, szonikus és szuperszonikus áramlás, amelyeket különböző sebességprofilok, nyomásviszonyok és hőátadási jellemzők jellemeznek.
Lamináris vs. turbulens áramlás
A gázáramlás átmenete laminárisból turbulensbe a következők alapján Reynolds-szám5, ami befolyásolja a nyomásveszteséget, a hőátadást és a keverési jellemzőket.
Reynolds-szám a gázáramláshoz:
Re = ρVD/μ
Hol:
- ρ = Gáz sűrűsége (a nyomástól és a hőmérséklettől függően változik)
- V = Átlagos sebesség
- D = csőátmérő
- μ = dinamikus viszkozitás
Áramlási rendszerek osztályozása:
| Reynolds-szám | Áramlási rendszer | Jellemzők |
|---|---|---|
| Re < 2300 | Lamináris | Zökkenőmentes, kiszámítható áramlás |
| 2300 < Re < 4000 | Átmenet | Instabil, vegyes viselkedés |
| Re > 4000 | Turbulens | Káosz, fokozott keveredés |
Szubszonikus áramlási rendszer
Szubszonikus áramlásról akkor beszélünk, amikor a gáz sebessége kisebb, mint a helyi hangsebesség, ami lehetővé teszi a nyomászavarok terjedését a folyásirányban.
Szubszonikus áramlási jellemzők:
- Mach-szám: M < 1.0
- Nyomás terjedése: A zavarok az árral szemben haladnak felfelé
- Áramlásszabályozás: A downstream feltételek az egész rendszerre hatással vannak
- Sűrűség változások: Mérsékelt, kiszámítható ingadozások
- Tervezési rugalmasság: Többféle megoldás lehetséges
Szubszonikus áramlási alkalmazások:
- A legtöbb ipari gázelosztó rendszer
- HVAC és szellőztető rendszerek
- Alacsony nyomású pneumatikus rendszerek
- Kémiai technológiai berendezések
- Erőművi gázkezelés
Sonic Flow (fojtott áramlás)
Szonikus áramlás akkor keletkezik, amikor a gáz sebessége megegyezik a hang helyi sebességével, ami egyedi jellemzőkkel bíró kritikus áramlási feltételeket teremt.
Sonic Flow tulajdonságok:
- Mach-szám: M = 1,0 pontosan
- Maximális tömegáram: Nem lehet túllépni
- Nyomás Függetlenség: A lefelé irányuló nyomás nem befolyásolja az áramlást
- Kritikus nyomásarány: Általában 0,53 körül van levegő esetén
- Hőmérsékleti hatások: Jelentős hőmérséklet-csökkenés
Sonic Flow alkalmazások:
- Gázturbina fúvókák
- Biztonsági túlnyomásos szelepek
- Áramlásmérő eszközök
- Rakétahajtóművek fúvókái
- Nagynyomású gázszabályozók
Szuperszonikus áramlási rendszer
A szuperszonikus áramlás akkor következik be, amikor a gáz sebessége meghaladja a hangsebességet, ami lökéshullámokat és egyedi áramlási jelenségeket hoz létre.
Szuperszonikus áramlási jellemzők:
- Mach-szám: M > 1.0
- Lökéshullámok: Hirtelen nyomás- és hőmérsékletváltozások
- Áramlási irány: Az információ nem tud felfelé haladni
- Tágulási hullámok: Sima nyomáscsökkentés
- Tervezési komplexitás: Speciális elemzést igényel
Lökéshullám típusok:
| Sokk típus | Jellemzők | Alkalmazások |
|---|---|---|
| Normál sokk | Az áramlásra merőlegesen | Diffúzorok, beömlőnyílások |
| Ferde sokk | Az áramlás irányába szögelve | Szuperszonikus repülőgépek |
| Bővítő ventilátor | Fokozatos nyomáscsökkentés | Fúvóka kialakítása |
Hiperszonikus áramlás
A hiperszonikus áramlás nagyon magas Mach-számoknál (jellemzően M > 5) jelentkezik, ahol további hatások válnak fontossá.
Hiperszonikus hatások:
- Valódi gázhatások: Az ideális gáztörvény megbomlik
- Kémiai reakciók: Dissociáció és ionizáció
- Hőátvitel: Szélsőséges fűtési hatások
- Viszkózus hatások: Határréteg kölcsönhatások
Hogyan számítsuk ki és optimalizáljuk a gázáramlást ipari alkalmazásokban?
A gázáramlási számítások speciális módszereket igényelnek, amelyek figyelembe veszik a kompresszibilitási hatásokat, míg az optimalizálás az energiafogyasztás minimalizálására és a rendszer teljesítményének maximalizálására összpontosít.
A gázáramlási számítások kompresszibilis áramlási egyenleteket, súrlódási tényező összefüggéseket és termodinamikai összefüggéseket használnak, míg az optimalizálás a csövek méretezését, a nyomásszint kiválasztását és a rendszer konfigurációját foglalja magában az energiaköltségek minimalizálása érdekében.
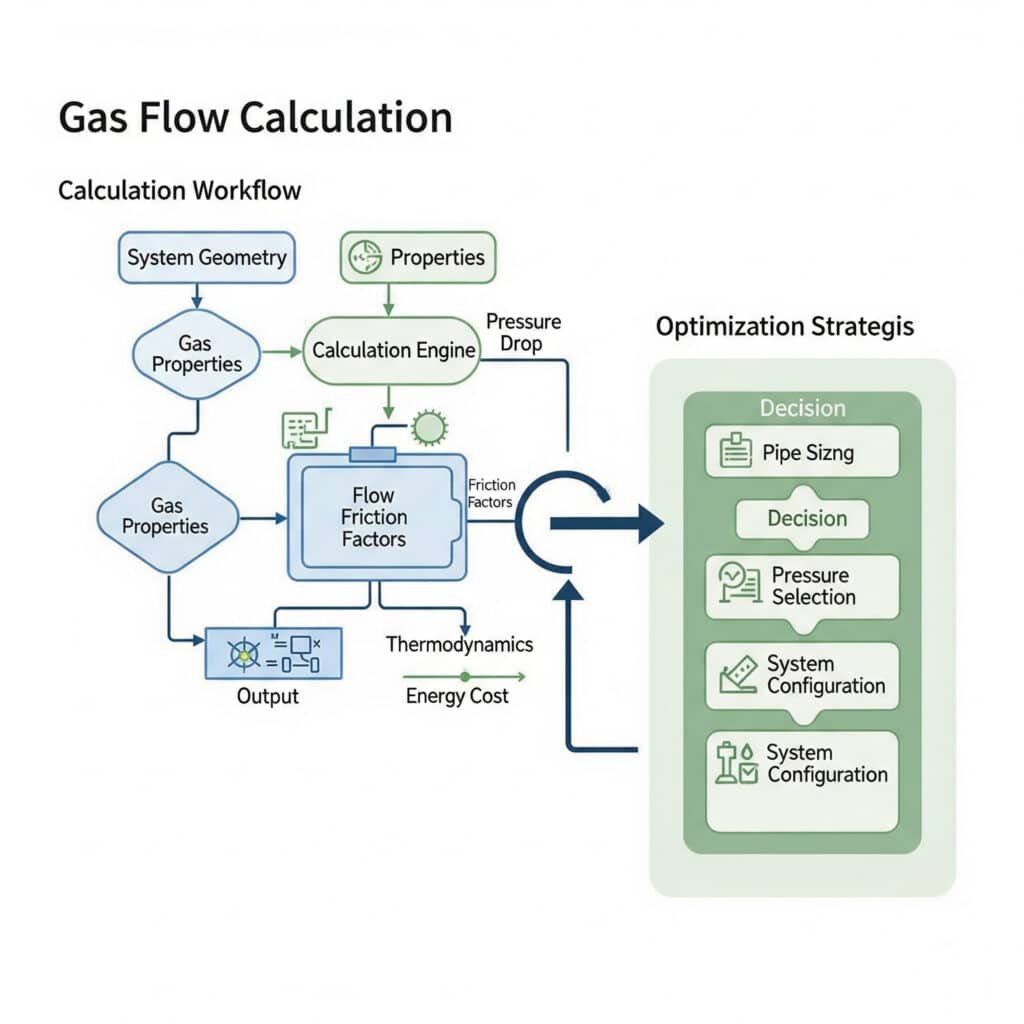
Alapvető gázáramlási számítások
A gázáramlási számítások a kompresszibilis áramlási hatások és a valós gáztulajdonságok figyelembevételével módosított alapegyenletekkel kezdődnek.
Tömegáramlás számítása:
ṁ = ρAV = (p/RT)AV
Egy nyíláson keresztül történő fojtott áramláshoz:
ṁ = CdA√(γρp)[2/(γ+1)]^((γ+1)/(2(γ-1)))
Hol:
- Cd = kisülési együttható
- A = nyílásfelület
- γ = fajlagos hőhányad
- ρ = feláramlási sűrűség
- p = Folyóirányú nyomás
Nyomásesés számítások
A gázáramlásra vonatkozó nyomásesés-számításoknak a súrlódási veszteségeken kívül figyelembe kell venniük a gáz tágulása miatti gyorsulási hatásokat is.
Teljes nyomásesés összetevői:
- Súrlódási nyomásesés: A fal nyírófeszültség miatt
- Gyorsulás nyomásesés: A sebességnövekedés miatt
- Emelkedés nyomásesés: A gravitációs hatások miatt
- Szerelvény nyomásesés: Az áramlási zavarok miatt
Súrlódási nyomásesés képlete:
Δpf = f(L/D)(ρV²/2)
Gyorsulási nyomásesés:
Δpa = ρ₂V₂² - ρ₁V₁² (területváltozások esetén)
Csővezeték áramláselemzés
A hosszú csővezetékek elemzése iteratív számításokat igényel a csővezeték hossza mentén változó gáztulajdonságok miatt.
Csővezeték-számítási lépések:
- Oszd meg a csővezetéket: Állandó tulajdonságokkal rendelkező szegmensekbe
- Szegmens tulajdonságok kiszámítása: Nyomás, hőmérséklet, sűrűség
- Az áramlási rendszer meghatározása: Lamináris vagy turbulens
- Nyomáscsökkenés kiszámítása: Minden egyes szegmens esetében
- Tulajdonságok frissítése: A következő szegmenshez
- Iterálni: A konvergencia eléréséig
Egyszerűsített csővezetéki egyenlet:
p₁² - p₂² = (fLṁ²RT)/(A²Dρ₀)
Hol:
- p₁, p₂ = bemeneti és kimeneti nyomások
- f = átlagos súrlódási tényező
- L = a csővezeték hossza
- ṁ = Tömegáramlás
- R = gázállandó
- T = Átlagos hőmérséklet
- A = A cső területe
- D = csőátmérő
- ρ₀ = Referenciasűrűség
Rendszeroptimalizálási stratégiák
A gázáramlási rendszer optimalizálása egyensúlyt teremt a tőkeköltségek, az üzemeltetési költségek és a teljesítménykövetelmények között a minimális életciklusköltségek elérése érdekében.
Optimalizálási paraméterek:
| Paraméter | A rendszerre gyakorolt hatás | Optimalizálási stratégia |
|---|---|---|
| Cső átmérője | Tőkeköltség vs. nyomásesés | Gazdasági átmérő számítása |
| Üzemi nyomás | Tömörítési költség vs. csőköltség | Nyomásszint optimalizálás |
| Kompresszor szakaszolás | Hatékonyság kontra komplexitás | A szakaszszám optimalizálása |
| Hőcserélő mérete | Hővisszanyerés vs. tőkeköltség | Gazdaságos hőcsere |
Gazdasági csőméretezés
A gazdaságos csőméretezés a cső tőkeköltségét a rendszer élettartama alatt a szivattyúzási energiaköltségekkel szemben egyensúlyba hozza.
Gazdasági átmérő képlet:
D_gazdasági = K(ṁ/ρ)^0,37
Ahol K függ:
- Energiaköltségek
- Csőköltség
- A rendszer élettartama
- Kamatláb
- Évi üzemórák
Áramlásmérés és szabályozás
A gázáramlás pontos mérése és szabályozása megköveteli a mérőeszközökre gyakorolt összenyomható áramlási hatások megértését.
Áramlásmérési megfontolások:
- Nyíláslemezek: Szükséges a kompresszibilitási korrekció
- Venturi mérők: Kevésbé érzékeny a tömöríthetőségre
- Turbina mérők: A gáz sűrűségének változása befolyásolja
- Ultrahangos mérők: Hőmérséklet-kompenzációt igényel
- Coriolis mérők: Közvetlen tömegáram-mérés
Számítógépes áramlástan (CFD)
Az összetett gázáramlási rendszerek számára előnyös a CFD-elemzés a teljesítmény optimalizálása és a különböző üzemi körülmények közötti viselkedés előrejelzése érdekében.
CFD alkalmazások:
- Komplex geometriák: Szabálytalan formák és szerelvények
- Hőátvitel: Kombinált áramlási és termikus elemzés
- Keverési elemzés: Gázösszetétel-változások
- Optimalizálás: Tervezési paraméterek vizsgálata
- Hibaelhárítás: Az áramlási problémák azonosítása
Nemrégiben együtt dolgoztam egy David Wilson nevű kanadai petrolkémiai mérnökkel Albertában, akinek gázfeldolgozó üzemében hatékonysági problémák léptek fel. A CFD-elemzés és a megfelelő gázáramlási számítások segítségével azonosítottuk a recirkulációs zónákat, amelyek 20% energiapazarlást okoztak. A tervezési módosítások végrehajtása után az energiafogyasztás 18%-tal csökkent, miközben nőtt a feldolgozási kapacitás.
Következtetés
A gázáramlási elvek a sűrűségváltozásokra módosított megmaradási törvények segítségével szabályozzák a kompresszibilis folyadékok viselkedését, ami olyan speciális elemzési módszereket igényel, amelyek figyelembe veszik a nyomás-hőmérséklet-sebesség kölcsönhatásokat és a folyadékáramlási rendszerektől alapvetően eltérő összenyomhatósági hatásokat.
GYIK a gázáramlási elvekről
Mi a gázáramlás alapelve?
A gázáramlás a tömeg, az impulzus és az energia megmaradása alapján működik, módosítva a kompresszibilis folyadékok viselkedésére, ahol a gáz sűrűsége a nyomással és a hőmérséklettel változik, sebesség-nyomás-hőmérséklet kölcsönhatásokat hozva létre.
Miben különbözik a gázáramlás a folyadékáramlástól?
A gázáramlás jelentős sűrűségváltozásokkal, szonikus sebességkorlátozásokkal, hőmérséklet-nyomás kapcsolattal és fojtott áramlási jelenségekkel jár, amelyek nem fordulnak elő az összenyomhatatlan folyadékáramlási rendszerekben.
Mi a fojtott áramlás a gázrendszerekben?
A fojtott áramlás akkor következik be, amikor a gáz sebessége eléri a szonikus feltételeket (Mach = 1,0), ami a maximális tömegáramot korlátozza, függetlenül az áramlás utáni nyomáscsökkentéstől, ami általában fúvókákban és vezérlőszelepekben fordul elő.
Hogyan számolja ki a gázáramlási sebességet?
A gázáram számítása az ṁ = ρAV egyenletet használja, ahol a sűrűség a nyomás és a hőmérséklet függvényében változik az ideális gáztörvény szerint, ami összetett rendszerek esetén iteratív megoldásokat igényel.
Milyen tényezők befolyásolják a gázáramlás viselkedését?
A legfontosabb tényezők közé tartoznak a gáz tulajdonságai (molekulatömeg, fajlagos hőhányad), a rendszer geometriája (csőátmérő, szerelvények), az üzemi körülmények (nyomás, hőmérséklet) és a hőátadási hatások.
Miért fontos a Mach-szám a gázáramlásban?
A Mach-szám (sebesség/hangsebesség) határozza meg az áramlási rendszer jellemzőit: a szubszonikus áramlás (M1) pedig lökéshullámokat generál.
-
Megmagyarázza az alapvető különbséget a kompresszibilis áramlás között, ahol a folyadék sűrűsége jelentősen változik a nyomással, és az inkompresszibilis áramlás között, ahol a sűrűség állandónak tekinthető, ami kulcsfontosságú különbség a gáz- és folyadékdinamika között. ↩
-
Áttekintést nyújt a Navier-Stokes-egyenletekről, a folyadékmechanika alapját képező parciális differenciálegyenletekről, amelyek a nyomatékmegőrzésen alapuló viszkózus folyadékok mozgását írják le. ↩
-
Részletesen meghatározza a Mach-számot, amely a folyadékdinamikában egy dimenziótlan mennyiség, amely az áramlási sebesség és a helyi hangsebesség hányadosát jelenti, és amelyet az áramlási rendszerek osztályozására használnak. ↩
-
A fojtott áramlás jelenségét írja le, amely a kompresszibilis áramlás olyan határállapota, amikor a tömegáram nem növekszik a nyomás további csökkenésével, mivel a sebesség a legszűkebb ponton elérte a hangsebességet. ↩
-
Magyarázza a Reynolds-számot, amely a folyadékmechanikában az áramlási minták előrejelzésére használt, döntő fontosságú dimenziótlan mennyiség, amely segít megkülönböztetni a lamináris (sima) és a turbulens (kaotikus) áramlási rendszereket. ↩


