Bagaimana Hambatan Aliran Sebenarnya Mempengaruhi Kinerja Sistem Pneumatik Anda?

Infografis teknis yang menjelaskan hambatan aliran dalam sistem pneumatik. Infografis ini menampilkan diagram pipa dengan bagian lurus yang diikuti dengan tikungan. Grafik yang diplot di atas pipa menunjukkan tingkat tekanan. Di sepanjang bagian lurus, tekanannya melandai ke bawah, yang diberi label 'Kerugian Gesekan'. Di tikungan, tekanan turun tajam dalam satu langkah, yang diberi label 'Kerugian Lokal'. Ilustrasi ini dengan jelas membedakan antara dua jenis hambatan dan efek kumulatifnya terhadap tekanan. — Resistensi Sebenarnya Mempengaruhi

Apakah Anda mengalami masalah dengan kecepatan silinder yang lambat, gerakan yang tidak konsisten, atau gaya yang tidak memadai dalam sistem pneumatik Anda? Masalah umum ini sering kali berasal dari penyebab yang disalahpahami: hambatan aliran. Banyak insinyur mengukur komponen pneumatik mereka hanya berdasarkan persyaratan tekanan dan gaya, mengabaikan dampak kritis dari hambatan aliran pada kinerja dunia nyata.

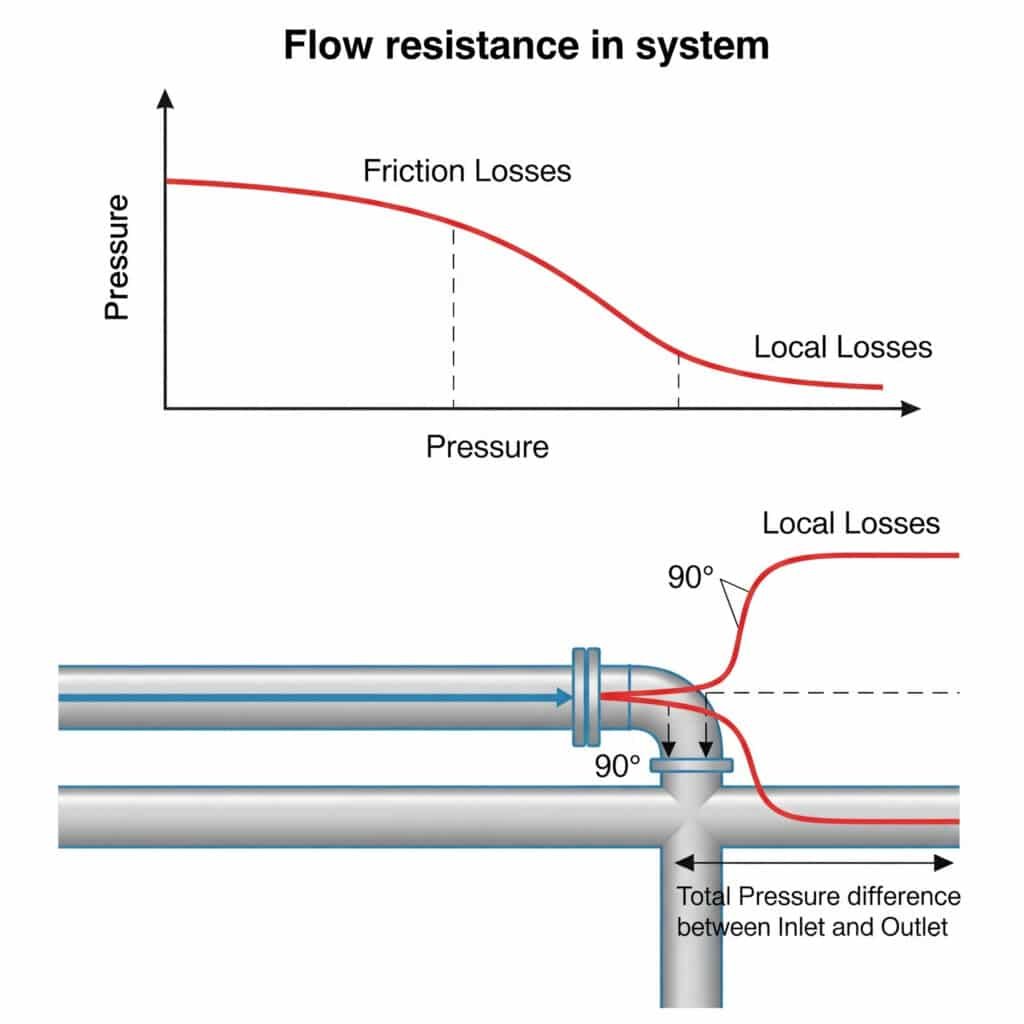
Hambatan aliran dalam sistem pneumatik menciptakan penurunan tekanan yang mengurangi gaya yang tersedia, membatasi kecepatan maksimum, dan menyebabkan gerakan yang tidak konsisten. Hambatan ini berasal dari gesekan di sepanjang pipa lurus (kerugian gesekan) dan gangguan pada alat kelengkapan, belokan, dan katup (kerugian lokal). Bersama-sama, resistensi ini dapat mengurangi kinerja sistem aktual sebesar 20-50% dibandingkan dengan perhitungan teoritis.

Selama lebih dari 15 tahun di Bepto bekerja dengan sistem pneumatik, saya telah melihat banyak kasus di mana memahami dan mengatasi hambatan aliran telah mengubah sistem yang berkinerja buruk menjadi operasi yang andal dan efisien. Izinkan saya membagikan apa yang telah saya pelajari tentang menghitung dan meminimalkan pembunuh kinerja tersembunyi ini.

Daftar Isi

Bagaimana Sebenarnya Anda Menghitung Kerugian Gesekan pada Saluran Pneumatik?
Mengapa Metode Panjang Ekuivalen Sangat Penting untuk Desain Sistem yang Akurat?
Apa yang Terjadi Ketika Udara Mengalir Melalui Bagian Lubang yang Diperkecil?
Kesimpulan
Tanya Jawab Tentang Hambatan Aliran dalam Sistem Pneumatik

Bagaimana Sebenarnya Anda Menghitung Kerugian Gesekan pada Saluran Pneumatik?

Kerugian gesekan pada pipa lurus dan tabung adalah dasar dari perhitungan hambatan aliran, tetapi banyak insinyur mengandalkan aturan praktis yang terlalu disederhanakan yang mengarah ke sistem yang berukuran kecil.

Kerugian gesekan pada saluran pneumatik dihitung dengan menggunakan Persamaan Darcy-Weisbach¹ΔP = λ(L/D)(ρv²/2), di mana λ adalah faktor gesekan, L adalah panjang pipa, D adalah diameter pipa, ρ adalah densitas udara, dan v adalah kecepatan aliran. Untuk sistem pneumatik, faktor gesekan λ bervariasi berdasarkan Bilangan Reynolds² dan kekasaran relatif, dan biasanya ditentukan dengan menggunakan tabel pencarian atau Diagram Moody³.

Memahami kerugian gesekan memiliki implikasi praktis untuk desain sistem dan pemecahan masalah. Izinkan saya menguraikannya menjadi wawasan yang dapat ditindaklanjuti.

Menggunakan Tabel Faktor Gesekan Secara Efektif

Faktor gesekan (λ) adalah parameter utama dalam menghitung penurunan tekanan, tetapi menentukan nilainya memerlukan pertimbangan kondisi aliran:

Rezim Aliran	Bilangan Reynolds (Re)	Penentuan Faktor Gesekan
Aliran Laminar	Re <2000	λ = 64/Re
Alur Transisi	2000 < Re < 4000	Tidak dapat diandalkan - hindari mendesain dalam kisaran ini
Aliran Turbulen	Re> 4000	Gunakan tabel pencarian berdasarkan kekasaran relatif (ε/D)

Tabel Pencarian Faktor Gesekan Praktis

Untuk aliran turbulen dalam sistem pneumatik, gunakan tabel yang disederhanakan ini:

Bahan Pipa	Kekasaran Relatif (ε/D)	Faktor Gesekan (λ) pada Bilangan Reynolds Umum
		Re = 10.000
Tabung Halus (PVC, Poliuretan)	0.0001 – 0.0005	0.031
Tabung Aluminium	0.001 – 0.002	0.035
Baja Galvanis	0.003 – 0.005	0.042
Baja Berkarat	0.01 – 0.05	0.054

Menghitung Penurunan Tekanan dalam Sistem Pneumatik Nyata

Mari kita bahas sebuah contoh praktis:

Parameter	Nilai/Perhitungan	Contoh
Diameter Pipa (D)	Diameter internal	8mm (0,008m)
Panjang Pipa (L)	Total panjang lurus	5m
Laju Aliran (Q)	Dari persyaratan sistem	20 liter standar/detik
Kepadatan Udara (ρ)	Pada tekanan operasi	7,2 kg/m³ pada 6 bar
Kecepatan Aliran (v)	v = Q/(π×D²/4)	v = 0,02 m³/s/(π × 0,008²/4) = 398 m/s
Bilangan Reynolds (Re)	Re = ρvD/μ	Re = 7,2 × 398 × 0,008 / 1,8 × 10-⁵ = 1.273.600
Kekasaran Relatif	Untuk tabung poliuretan	0.0003
Faktor Gesekan (λ)	Dari tabel pencarian	0.017
Penurunan Tekanan (ΔP)	ΔP = λ (L/D) (ρv²/2)	ΔP = 0,017 × (5/0,008) × (7,2 × 398²/2) = 6,07 bar

Aplikasi Dunia Nyata: Memecahkan Masalah Kecepatan Silinder

Tahun lalu, saya bekerja dengan Sarah, seorang insinyur manufaktur di sebuah perusahaan peralatan pengemasan di Wisconsin. Sistem silinder tanpa batangnya hanya beroperasi pada kecepatan 60% dari kecepatan yang diharapkan, meskipun memiliki silinder dengan ukuran yang tepat dan tekanan suplai yang memadai.

Setelah menganalisis sistemnya, saya menemukan bahwa dia menggunakan pipa 6mm untuk aplikasi aliran tinggi. Kerugian gesekan menyebabkan penurunan tekanan sebesar 2,1 bar, yang secara signifikan mengurangi kekuatan dan kecepatan yang tersedia. Dengan meningkatkan ke pipa 10mm, kami mengurangi penurunan tekanan hingga 0,4 bar, dan sistemnya segera mencapai kinerja yang diperlukan tanpa perubahan lainnya.

Faktor-faktor yang Mempengaruhi Kerugian Gesekan dalam Sistem Nyata

Beberapa faktor mempengaruhi kerugian gesekan yang sebenarnya:

Suhu udara: Temperatur yang lebih tinggi meningkatkan viskositas dan gesekan
Kontaminasi: Kotoran dan minyak dapat meningkatkan kekasaran yang efektif
Pembengkokan tabung: Deformasi mikro pada tabung bengkok meningkatkan resistensi
Kemunduran usia: Korosi dan endapan meningkatkan kekasaran dari waktu ke waktu
Tekanan operasi: Tekanan yang lebih tinggi meningkatkan densitas dan kerugian

Mengapa Metode Panjang Ekuivalen Sangat Penting untuk Desain Sistem yang Akurat?

Kehilangan lokal pada fitting, katup, dan belokan sering kali melebihi kehilangan gesekan pada pipa lurus, namun banyak insinyur yang mengabaikannya atau menggunakan metode estimasi kasar yang menyebabkan masalah kinerja.

Metode panjang ekuivalen mengubah kerugian lokal dari alat kelengkapan dan katup menjadi panjang ekuivalen pipa lurus yang akan menyebabkan penurunan tekanan yang sama. Hal ini dihitung dengan menggunakan Le = K (D/λ), di mana Le adalah panjang ekuivalen, K adalah koefisien kerugian lokal⁴dengan D adalah diameter pipa, dan λ adalah faktor gesekan. Metode ini menyederhanakan penghitungan dan memberikan prediksi kinerja sistem yang lebih akurat.

Mari kita telusuri cara menerapkan metode ini secara efektif dalam desain sistem pneumatik.

Tabel Panjang Ekuivalen untuk Komponen Pneumatik Umum

Berikut ini adalah tabel referensi praktis untuk komponen pneumatik yang umum:

Komponen	Nilai-K	Panjang Ekuivalen (Le/D)
Siku 90° (tajam)	0.9	30
Siku 90° (radius standar)	0.3	10
Siku 45°	0.2	7
Pertigaan (arus lalu lintas)	0.3	10
Pertigaan (aliran cabang)	1.0	33
Katup Bola (terbuka penuh)	0.1	3
Katup Gerbang (terbuka penuh)	0.2	7
Kopling Sambungan Cepat	0.4-0.8	13-27
Katup Periksa	1.5-2.5	50-83
Katup Kontrol Aliran Standar	1.0-3.0	33-100

Menerapkan Metode Panjang Ekuivalen

Untuk menggunakan metode ini secara efektif:

Identifikasi semua komponen dalam sirkuit pneumatik Anda
Temukan nilai-K atau rasio panjang ekuivalen (Le/D) untuk setiap komponen
Hitung panjang ekuivalen dengan mengalikannya dengan diameter pipa
Tambahkan semua panjang yang setara dengan panjang pipa lurus yang sebenarnya
Gunakan total panjang efektif dalam perhitungan kehilangan gesekan Anda

Sebagai contoh, sistem dengan 5 m pipa 8mm lurus ditambah empat siku 90°, satu persimpangan T, dan dua sambungan cepat:

Komponen	Kuantitas	Le/D	Panjang Setara
Siku 90°	4	10	4 × 10 × 0,008m = 0,32m
Pertigaan	1	10	1 × 10 × 0,008m = 0,08m
Koneksi Cepat	2	20	2 × 20 × 0,008m = 0,32m
Total Panjang Ekuivalen			0.72m
Panjang Lurus Aktual			5.00m
Total Panjang Efektif			5.72m

Ini berarti sistem 5m Anda benar-benar berperilaku seperti sistem 5,72m karena kehilangan lokal - peningkatan 14,4% dalam panjang efektif.

Studi Kasus: Mengoptimalkan Penempatan Katup dalam Sistem Perakitan

Baru-baru ini saya membantu Miguel, seorang insinyur otomasi di pabrik perakitan elektronik di Arizona. Sistem pick-and-place miliknya mengalami gerakan yang tidak konsisten dan variasi waktu siklus, meskipun menggunakan komponen berkualitas tinggi.

Analisis mengungkapkan bahwa manifold katupnya terletak 3m dari silinder, dan sirkuitnya memiliki banyak alat kelengkapan. Perhitungan panjang yang setara menunjukkan bahwa jarak aktual 3m memiliki panjang efektif 7,2m karena kerugian lokal-lebih dari dua kali lipat jarak pipa lurus!

Dengan merelokasi manifold katup lebih dekat ke silinder dan menghilangkan beberapa alat kelengkapan, kami mengurangi panjang efektif dari 7,2 m menjadi 2,1 m. Hal ini menurunkan penurunan tekanan sebesar 70%, sehingga menghasilkan gerakan yang konsisten dan pengurangan waktu siklus sebesar 15%.

Kiat Praktis untuk Meminimalkan Kerugian Lokal

Untuk mengurangi kerugian lokal dalam sistem pneumatik Anda:

Gunakan siku yang disapu atau dibulatkan alih-alih tikungan tajam (mengurangi nilai K sebesar 67%)
Meminimalkan jumlah alat kelengkapan dengan merencanakan rute yang lebih langsung
Pilih komponen dengan batasan rendah seperti katup bola bor penuh jika diperlukan
Ukuran alat kelengkapan dengan benar - alat kelengkapan yang terlalu kecil menyebabkan kerugian yang tidak proporsional
Tempatkan katup dekat dengan aktuator untuk meminimalkan panjang tabung yang efektif

Apa yang Terjadi Ketika Udara Mengalir Melalui Bagian Lubang yang Diperkecil?

Bagian lubang yang berkurang di sirkuit pneumatik - seperti katup yang tertutup sebagian, alat kelengkapan berukuran kecil, atau transisi diameter - menciptakan pembatasan aliran yang signifikan yang dapat sangat memengaruhi kinerja sistem.

Ketika udara mengalir melalui bagian lubang yang diperkecil, penurunan tekanan⁵ terjadi sesuai dengan rumus ΔP = ρ(v₂² - v₁²)/2, di mana v₁ adalah kecepatan sebelum pembatasan dan v₂ adalah kecepatan dalam pembatasan. Hal ini dapat dikompensasi dengan menggunakan faktor kompensasi rasio lubang C = (1 - (d/D)⁴), di mana d adalah diameter yang diperkecil dan D adalah diameter asli. Faktor ini membantu memprediksi performa sistem yang sesungguhnya dan menghindari komponen yang terlalu kecil.

Mari kita jelajahi implikasi praktis dari bagian lubang yang diperkecil dan bagaimana memperhitungkannya dalam desain sistem.

Menghitung Penurunan Tekanan pada Transisi Diameter

Ketika udara mengalir dari diameter yang lebih besar ke diameter yang lebih kecil, penurunan tekanan dapat dihitung dengan menggunakan:

Parameter	Formula	Contoh
Diameter Asli (D)	Dari spesifikasi	10mm
Diameter Berkurang (d)	Dari spesifikasi	6mm
Rasio Bore (d/D)	Pembagian sederhana	0.6
Laju Aliran (Q)	Dari persyaratan sistem	15 liter standar/detik
Kecepatan dalam Pipa Asli (v₁)	v₁ = Q / (π × D² / 4)	191 m/s
Kecepatan pada Bagian yang Diperkecil (v₂)	v₂ = Q/(π×d²/4)	531 m/s
Penurunan Tekanan (ΔP)	ΔP = ρ (v₂² - v₁²) / 2	0,88 bar
Faktor Kompensasi (C)	C = (1 - (d/D)⁴)	0.87

Skenario Pengurangan Lubang Bor yang Umum dan Dampaknya

Berikut ini adalah bagaimana pengurangan lubang yang berbeda mempengaruhi kapasitas aliran:

Pengurangan Lubang	Pengurangan Kapasitas Aliran	Peningkatan Penurunan Tekanan
10mm hingga 8mm	36%	2.4×
10mm hingga 6mm	64%	7.7×
10mm hingga 4mm	84%	39×
8mm hingga 6mm	44%	3.2×
8mm hingga 4mm	75%	16×
6mm hingga 4mm	56%	5.1×

Angka-angka ini menyoroti mengapa pengurangan diameter yang tampaknya kecil dapat memiliki efek dramatis pada performa sistem.

Efek Kumulatif dari Beberapa Pembatasan

Dalam sirkuit pneumatik yang sesungguhnya, beberapa pembatasan terjadi secara seri. Efeknya bersifat kumulatif dan dapat dihitung dengan menggunakan:

Konversikan setiap batasan ke faktor C yang setara
Hitung faktor-C total: Ctotal = 1 - (1-C₁)(1-C₂)(1-C₃)...
Gunakan faktor total ini untuk menentukan pengurangan kinerja sistem secara keseluruhan

Studi Kasus: Memecahkan Masalah Ketidakcocokan Katup-Aktuator

Bulan lalu, saya bekerja dengan Thomas, seorang supervisor pemeliharaan di sebuah pabrik furnitur di North Carolina. Sistem silinder tanpa batang barunya beroperasi kurang dari setengah kecepatan yang diharapkan, meskipun menggunakan ukuran katup yang direkomendasikan pabrikan.

Investigasi mengungkapkan beberapa pengurangan lubang di sirkuitnya:

Jalur suplai 10mm ke port katup 8mm (C₁ = 0,36)
Port katup 8mm ke fitting 6mm (C₂ = 0,44)
Fitting 6mm ke port silinder 8mm dengan batasan internal (C₃ = 0,32)

Faktor kompensasi totalnya adalah Ctotal = 1 - (1-0.36)(1-0.44)(1-0.32) = 0.75, yang berarti sistemnya kehilangan 75% dari kapasitas aliran teoritisnya!

Dengan meningkatkan ke komponen dengan ukuran yang tepat di seluruh sistem, kami menghilangkan batasan ini dan mencapai kinerja yang diperlukan tanpa mengubah silinder atau tekanan suplai.

Strategi Praktis untuk Meminimalkan Kerugian Pengurangan Lubang Bor

Untuk mengurangi kerugian dari pengurangan lubang bor:

Ukuran komponen secara konsisten di seluruh sirkuit pneumatik
Gunakan ukuran tabung praktis terbesar untuk aplikasi aliran tinggi
Perhatikan pembatasan komponen internalbukan hanya ukuran koneksi
Pertimbangkan jalur aliran paralel untuk kebutuhan aliran tinggi
Menghilangkan adaptor dan transisi yang tidak perlu sedapat mungkin

Prinsip "Tautan Terlemah" dalam Sistem Pneumatik

Ingatlah bahwa kinerja sistem pneumatik Anda dibatasi oleh komponen yang paling membatasi. Satu elemen berukuran kecil dapat meniadakan manfaat dari komponen berukuran tepat di tempat lain dalam sistem.

Sebagai contoh, sistem dengan tabung 10mm, katup 10mm, tetapi fitting 6mm pada silinder akan berkinerja pada dasarnya sama dengan sistem dengan komponen 6mm secara keseluruhan-dengan biaya yang lebih tinggi.

Kesimpulan

Memahami dan menghitung hambatan aliran dengan benar - melalui tabel faktor gesekan, metode panjang ekuivalen, dan kompensasi lubang yang dikurangi - sangat penting untuk merancang sistem pneumatik yang berkinerja seperti yang diharapkan dalam kondisi dunia nyata. Dengan menerapkan metode perhitungan dan prinsip-prinsip desain ini, Anda dapat mengoptimalkan aplikasi silinder tanpa batang dan sistem pneumatik lainnya untuk kinerja dan keandalan maksimum.

Tanya Jawab Tentang Hambatan Aliran dalam Sistem Pneumatik

Berapa banyak penurunan tekanan yang dapat diterima dalam sistem pneumatik?

Penurunan tekanan yang dapat diterima tergantung pada kebutuhan aplikasi Anda, tetapi sebagai pedoman umum, batasi penurunan tekanan total hingga 10-15% tekanan suplai untuk pengoperasian yang efisien. Untuk sistem 6 bar, ini berarti menjaga penurunan tekanan total di bawah 0,6-0,9 bar. Aplikasi kritis mungkin memerlukan penurunan tekanan yang lebih rendah lagi, yaitu 5-8% untuk mempertahankan kinerja yang konsisten.

Apa hubungan antara diameter tabung dan penurunan tekanan?

Penurunan tekanan berbanding terbalik dengan pangkat lima diameter (D⁵) untuk aliran turbulen dalam sistem pneumatik. Ini berarti menggandakan diameter tabung akan mengurangi penurunan tekanan sekitar 32 kali lipat. Sebagai contoh, meningkatkan dari tabung 6mm ke 12mm dapat mengurangi penurunan tekanan dari 1,5 bar menjadi hanya 0,047 bar dalam kondisi aliran yang sama.

Bagaimana cara menentukan ukuran tabung yang tepat untuk aplikasi pneumatik saya?

Pilih ukuran tabung berdasarkan persyaratan laju aliran dan penurunan tekanan yang dapat diterima. Hitung angka Reynolds dan faktor gesekan, kemudian gunakan persamaan Darcy-Weisbach untuk menentukan penurunan tekanan untuk diameter yang berbeda. Pilih diameter terkecil yang menjaga penurunan tekanan dalam batas yang dapat diterima (biasanya <10% tekanan suplai) sambil mempertimbangkan keterbatasan ruang dan biaya.

Apa yang menciptakan lebih banyak batasan: siku 90° atau pipa lurus sepanjang 5 meter?

Siku tajam 90° biasanya menciptakan resistensi yang setara dengan 30 diameter pipa dari pipa lurus. Untuk pipa 8mm, satu siku tajam setara dengan sekitar 240mm (30 × 8mm) pipa lurus. Ini berarti bahwa 5 meter pipa lurus menciptakan hambatan sekitar 21 kali lebih banyak daripada satu siku. Namun, sistem sering kali mengandung beberapa siku dan alat kelengkapan, yang efek kumulatifnya dapat melebihi kerugian panjang lurus.

Bagaimana alat kelengkapan sambungan cepat memengaruhi kinerja sistem?

Fitting sambungan cepat standar biasanya menimbulkan kehilangan lokal yang setara dengan 15-25 diameter pipa pipa lurus. Lebih penting lagi, banyak sambungan cepat memiliki batasan internal yang lebih kecil dari ukuran nominalnya. Sambungan cepat "10mm" mungkin memiliki batasan internal hanya 7-8mm, menciptakan pengurangan lubang yang dapat mengurangi kapasitas aliran sebesar 50-70% pada saat itu.

Apa dampak dari katup kontrol aliran yang tertutup sebagian pada kinerja sistem?

Katup kontrol aliran yang ditutup hingga 50% dari area lubang penuhnya tidak mengurangi aliran hanya sebesar 50% - ini mengurangi aliran sekitar 75% karena hubungan non-linier antara diameter dan kapasitas aliran. Penurunan tekanan meningkat sesuai dengan kuadrat perubahan kecepatan, sehingga mengurangi separuh diameter efektif meningkatkan penurunan tekanan sekitar 16 kali lipat dalam kondisi aliran yang sama.

Memberikan rincian rinci dari persamaan Darcy-Weisbach, sebuah formula fundamental dan banyak digunakan dalam dinamika fluida untuk menghitung kehilangan tekanan akibat gesekan dalam pipa. ↩
Menawarkan definisi yang jelas tentang bilangan Reynolds, sebuah kuantitas penting tanpa dimensi yang digunakan untuk memprediksi pola aliran (laminar atau turbulen) dalam situasi aliran fluida yang berbeda. ↩
Menyajikan diagram Moody, grafik komprehensif yang memplot faktor gesekan Darcy terhadap angka Reynolds dan kekasaran relatif, yang merupakan alat standar bagi para insinyur untuk menentukan penurunan tekanan dalam pipa. ↩
Menjelaskan konsep nilai-K, atau koefisien kehilangan lokal, angka tanpa dimensi yang digunakan untuk mengkarakterisasi kehilangan tekanan pada fitting pipa atau katup sebagai bagian dari metode panjang ekuivalen. ↩
Merinci fisika di balik penurunan tekanan yang terjadi ketika fluida melewati sebuah batasan (orifice), berdasarkan prinsip-prinsip persamaan kontinuitas dan prinsip Bernoulli. ↩

Halo, saya Chuck, seorang ahli senior dengan pengalaman 15 tahun di industri pneumatik. Di Bepto Pneumatic, saya fokus untuk memberikan solusi pneumatik berkualitas tinggi yang dibuat khusus untuk klien kami. Keahlian saya meliputi otomasi industri, desain dan integrasi sistem pneumatik, serta aplikasi dan pengoptimalan komponen utama. Jika Anda memiliki pertanyaan atau ingin mendiskusikan kebutuhan proyek Anda, jangan ragu untuk menghubungi saya di chuck@bepto.com.