
Apakah Anda kesulitan memprediksi kinerja aktual silinder pneumatik Anda? Banyak insinyur salah menghitung output gaya dan kebutuhan tekanan, yang menyebabkan kegagalan sistem dan waktu henti yang mahal. Tetapi ada cara sederhana untuk menguasai perhitungan ini.
Silinder pneumatik beroperasi sesuai dengan prinsip-prinsip fisika dasar, terutama Hukum Pascal1yang menyatakan bahwa tekanan yang diterapkan pada fluida terbatas disalurkan secara merata ke segala arah. Hal ini memungkinkan kita untuk menghitung gaya silinder dengan mengalikan tekanan dengan area piston yang efektif, dengan laju aliran dan unit tekanan yang memerlukan konversi yang tepat untuk desain sistem yang akurat.
Saya telah menghabiskan lebih dari satu dekade membantu pelanggan mengoptimalkan sistem pneumatik mereka, dan saya telah melihat bagaimana memahami prinsip-prinsip dasar ini dapat mengubah keandalan sistem. Izinkan saya berbagi pengetahuan praktis yang akan membantu Anda menghindari kesalahan umum yang saya lihat setiap hari.
Daftar Isi
- Bagaimana Hukum Pascal Menentukan Output Gaya Silinder?
- Apa Hubungan Antara Aliran Udara dan Tekanan dalam Silinder?
- Mengapa Memahami Konversi Satuan Tekanan Sangat Penting untuk Desain Sistem?
- Kesimpulan
- Tanya Jawab Tentang Fisika dalam Sistem Pneumatik
Bagaimana Hukum Pascal Menentukan Output Gaya Silinder?
Memahami Hukum Pascal merupakan hal mendasar untuk memprediksi dan mengoptimalkan kinerja silinder dalam sistem pneumatik apa pun.
Hukum Pascal menyatakan bahwa tekanan yang diberikan pada fluida dalam sistem tertutup disalurkan secara merata ke seluruh fluida. Untuk silinder pneumatik, ini berarti output gaya sama dengan tekanan dikalikan dengan area piston efektif (F = P × A). Hubungan sederhana ini adalah dasar untuk semua perhitungan gaya silinder.

Penurunan Perhitungan Gaya
Mari kita uraikan derivasi matematis dari perhitungan gaya silinder:
Persamaan Gaya Dasar
Persamaan dasar untuk gaya silinder adalah:
F = P × A
Dimana:
- F = Output gaya (N)
- P = Tekanan (Pa)
- A = Area piston efektif (m²)
Pertimbangan Area Efektif
Area efektif berbeda, tergantung pada jenis dan arah silinder:
| Jenis Silinder | Kekuatan Ekstensi | Kekuatan Retraksi |
|---|---|---|
| Aksi tunggal | P × A | Hanya gaya pegas |
| Kerja ganda (standar) | P × A | P × (A - a) |
| Kerja ganda (tanpa batang) | P × A | P × A |
Dimana:
- A = Area piston penuh
- a = Luas penampang batang
Saya pernah berkonsultasi dengan pabrik manufaktur di Ohio yang mengalami kekurangan tenaga dalam aplikasi pengepresan mereka. Perhitungan mereka tampak benar di atas kertas, tetapi performa aktualnya kurang. Setelah diselidiki, saya menemukan bahwa mereka menggunakan mengukur tekanan2 dalam perhitungan mereka, bukan tekanan absolut, dan mereka tidak memperhitungkan area batang selama retraksi. Setelah menghitung ulang dengan rumus dan nilai tekanan yang benar, kami dapat mengukur sistem mereka dengan benar, meningkatkan produktivitas sebesar 23%.
Contoh Perhitungan Gaya Praktis
Mari kita periksa beberapa perhitungan dunia nyata:
Contoh 1: Gaya Perpanjangan pada Silinder Standar
Untuk silinder dengan:
- Diameter lubang = 50mm (radius = 25mm = 0,025m)
- Tekanan operasi = 6 bar (600.000 Pa)
Area piston:
A = π × r² = π × (0,025)² = 0,001963 m²
Kekuatan ekstensi adalah:
F = P × A = 600.000 Pa × 0,001963 m² = 1.178 N ≈ 118 kg gaya
Contoh 2: Gaya Retraksi dalam Silinder yang Sama
Jika diameter batang 20mm (radius = 10mm = 0,01m):
Area batang adalah:
a = π × r² = π × (0,01)² = 0,000314 m²
Area retraksi yang efektif adalah:
A - a = 0,001963 - 0,000314 = 0,001649 m²
Gaya retraksi adalah:
F = P × (A - a) = 600.000 Pa × 0,001649 m² = 989 N ≈ gaya 99 kg
Faktor Efisiensi dalam Aplikasi Dunia Nyata
Dalam aplikasi praktis, ada beberapa faktor yang memengaruhi penghitungan gaya teoretis:
Kerugian Gesekan
Gesekan antara seal piston dan dinding silinder mengurangi gaya efektif:
| Jenis Segel | Faktor Efisiensi Khas |
|---|---|
| NBR standar | 0.85-0.90 |
| PTFE gesekan rendah | 0.90-0.95 |
| Segel yang sudah tua / usang | 0.70-0.85 |
Persamaan Gaya Praktis
Persamaan gaya dunia nyata yang lebih akurat adalah:
F_aktual = η × P × A
Dimana:
- η (eta) = Faktor efisiensi (biasanya 0,85-0,95)
Apa Hubungan Antara Aliran Udara dan Tekanan dalam Silinder?
Memahami hubungan antara laju aliran dan tekanan sangat penting untuk menentukan ukuran sistem pasokan udara dan memprediksi kecepatan silinder.
Aliran dan tekanan udara dalam sistem pneumatik berhubungan terbalik-karena tekanan meningkat, aliran biasanya menurun. Hubungan ini mengikuti hukum gas dan dipengaruhi oleh batasan, suhu, dan volume sistem. Pengoperasian silinder yang tepat membutuhkan keseimbangan faktor-faktor ini untuk mencapai kecepatan dan gaya yang diinginkan.
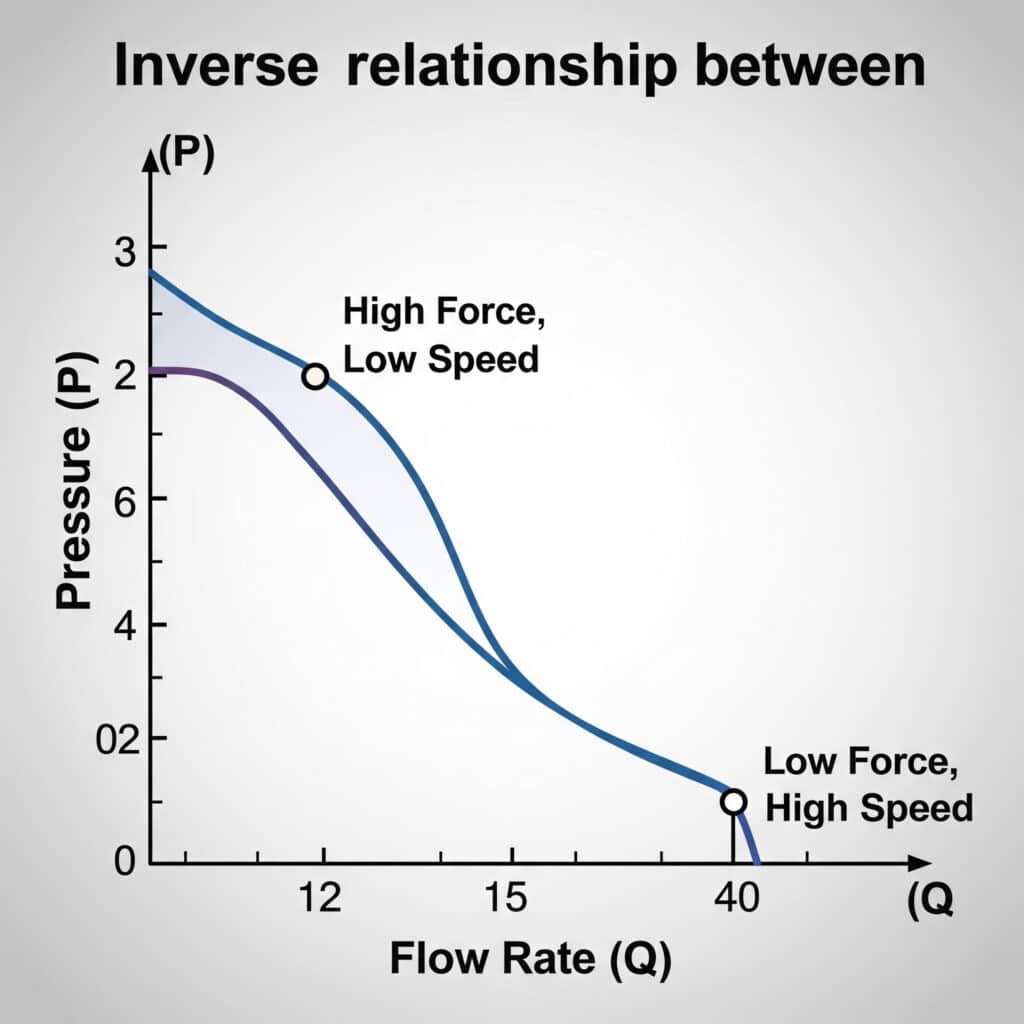
Tabel Konversi Aliran-Tekanan
Tabel referensi praktis ini menunjukkan hubungan antara laju aliran dan penurunan tekanan di berbagai komponen sistem:
| Ukuran Pipa (mm) | Laju Aliran (l/menit) | Penurunan Tekanan (bar/meter) pada Pasokan 6 bar |
|---|---|---|
| 4 | 100 | 0.15 |
| 4 | 200 | 0.45 |
| 4 | 300 | 0.90 |
| 6 | 200 | 0.08 |
| 6 | 400 | 0.25 |
| 6 | 600 | 0.50 |
| 8 | 400 | 0.06 |
| 8 | 800 | 0.18 |
| 8 | 1200 | 0.35 |
| 10 | 600 | 0.04 |
| 10 | 1200 | 0.12 |
| 10 | 1800 | 0.24 |
Matematika Aliran dan Tekanan
Hubungan antara aliran dan tekanan mengikuti beberapa hukum gas:
Persamaan Poiseuille3 untuk Aliran Laminar
Untuk aliran laminar melalui pipa:
Q = (π × r⁴ × ΔP) / (8 × η × L)
Dimana:
- Q = Laju aliran volumetrik
- r = Jari-jari pipa
- ΔP = Perbedaan tekanan
- η = Viskositas dinamis
- L = Panjang pipa
Koefisien Aliran (Cv)4 Metode
Untuk komponen seperti katup:
Q = Cv × √ΔP
Dimana:
- Q = Laju aliran
- Cv = Koefisien aliran
- ΔP = Penurunan tekanan di seluruh komponen
Perhitungan Kecepatan Silinder
Kecepatan silinder pneumatik bergantung pada laju aliran dan area silinder:
v = Q / A
Dimana:
- v = Kecepatan silinder (m/s)
- Q = Laju aliran (m³/s)
- A = Area piston (m²)
Selama proyek baru-baru ini di fasilitas pengemasan di Prancis, saya menemukan situasi di mana silinder tanpa batang klien bergerak terlalu lambat meskipun tekanannya memadai. Dengan menganalisis sistem mereka menggunakan perhitungan tekanan aliran kami, kami mengidentifikasi jalur suplai yang terlalu kecil yang menyebabkan penurunan tekanan yang signifikan. Setelah meningkatkan dari tabung 6mm ke 10mm, waktu siklus mereka meningkat sebesar 40%, yang secara dramatis meningkatkan kapasitas produksi.
Pertimbangan Aliran Kritis
Beberapa faktor memengaruhi hubungan aliran-tekanan dalam sistem pneumatik:
Fenomena Aliran Tersendat5
Ketika rasio tekanan melebihi nilai kritis (sekitar 0,53 untuk udara), aliran menjadi "tersendat" dan tidak dapat meningkat terlepas dari pengurangan tekanan hilir.
Efek Suhu
Laju aliran dipengaruhi oleh suhu menurut hubungan tersebut:
Q₂ = Q₁ × √(T₂/T₁)
Dimana:
- Q₁, Q₂ = Laju aliran pada suhu yang berbeda
- T₁, T₂ = Suhu absolut
Mengapa Memahami Konversi Satuan Tekanan Sangat Penting untuk Desain Sistem?
Menavigasi berbagai unit tekanan yang digunakan di seluruh dunia sangat penting untuk desain sistem yang tepat dan kompatibilitas internasional.
Konversi satuan tekanan sangat penting karena komponen dan spesifikasi pneumatik menggunakan satuan yang berbeda tergantung pada wilayah dan industri. Salah menafsirkan satuan dapat menyebabkan kesalahan perhitungan yang signifikan, dengan konsekuensi yang berpotensi berbahaya. Konversi antara tekanan absolut, pengukur, dan diferensial menambah lapisan kerumitan lainnya.
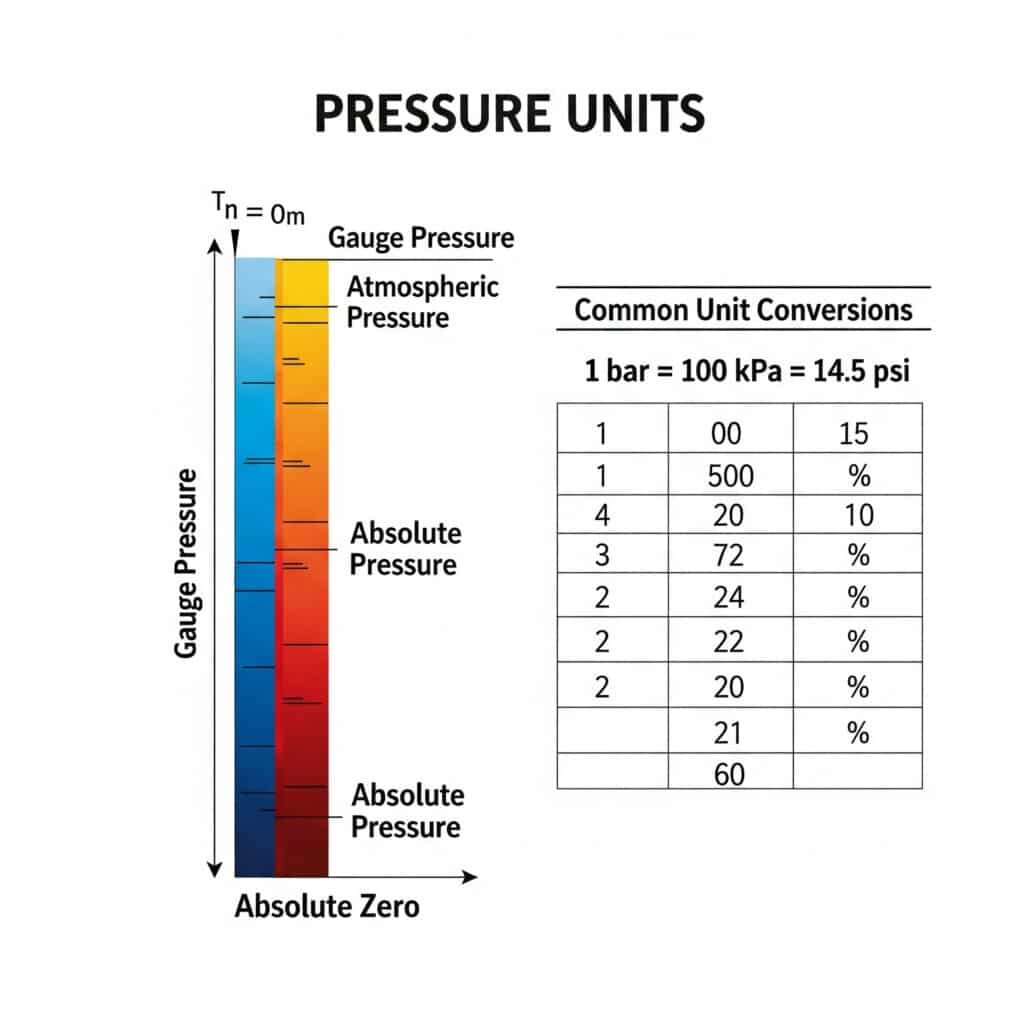
Panduan Konversi Satuan Tekanan Absolut
Tabel konversi yang komprehensif ini membantu menavigasi berbagai satuan tekanan yang digunakan secara global:
| Unit | Simbol | Setara dengan Pa | Setara dengan batang | Setara dengan psi |
|---|---|---|---|---|
| Pascal | Pa | 1 | 1 × 10-⁵ | 1.45 × 10-⁴ |
| Bar | bar | 1 × 10⁵ | 1 | 14.5038 |
| Pound per inci persegi | psi | 6,894.76 | 0.0689476 | 1 |
| Kilogram-gaya per cm persegi | kgf / cm² | 98,066.5 | 0.980665 | 14.2233 |
| Megapascal | MPa | 1 × 10⁶ | 10 | 145.038 |
| Suasana | atm | 101,325 | 1.01325 | 14.6959 |
| Torr | Torr | 133.322 | 0.00133322 | 0.0193368 |
| Milimeter merkuri | mmHg | 133.322 | 0.00133322 | 0.0193368 |
| Inci air | dalam H₂O | 249.089 | 0.00249089 | 0.0361274 |
Tekanan Absolut vs Tekanan Pengukur
Memahami perbedaan antara tekanan absolut dan tekanan pengukur adalah hal yang mendasar:
Kalkulator Konversi Tekanan
Konverter Unit Tekanan
Konverter Laju Aliran Silinder
Rumus Konversi
- P_absolute = P_gauge + P_atmosfer
- P_gauge = P_absolute - P_atmosfer
Kira-kira tekanan atmosfer standar:
- 1,01325 bar
- 14,7 psi
- 101.325 Pa
Saya pernah bekerja dengan tim teknik di Jerman yang telah membeli silinder tanpa batang kami, tetapi melaporkan bahwa mereka tidak mencapai gaya yang diharapkan. Setelah melakukan beberapa pemecahan masalah, kami menemukan bahwa mereka menggunakan grafik gaya kami (yang didasarkan pada tekanan pengukur) tetapi memasukkan nilai tekanan absolut. Kesalahpahaman sederhana ini menyebabkan kesalahan perhitungan sebesar 1 bar dalam ekspektasi gaya mereka. Setelah mengklarifikasi referensi tekanan, sistem mereka bekerja dengan tepat seperti yang ditentukan.
Contoh Konversi Praktis
Mari kita bahas beberapa skenario konversi yang umum:
Contoh 1: Mengonversi Tekanan Kerja di Seluruh Unit
Silinder dengan tekanan kerja maksimum 0,7 MPa:
Di bar:
0,7 MPa × 10 bar/MPa = 7 bar
Dalam psi:
0,7 MPa × 145,038 psi/MPa = 101,5 psi
Contoh 2: Mengonversi dari Pengukur ke Tekanan Absolut
Sistem yang beroperasi pada tekanan pengukur 6 bar:
Dalam tekanan absolut (bar):
6 bar_gauge + 1,01325 bar_atmosfer = 7,01325 bar_absolute
Contoh 3: Mengonversi dari kgf/cm² ke MPa
Silinder Jepang yang ditentukan untuk 7 kgf/cm²:
Dalam MPa:
7 kgf/cm² × 0,0980665 MPa/(kgf/cm²) = 0,686 MPa
Preferensi Unit Tekanan Regional
Wilayah yang berbeda biasanya menggunakan satuan tekanan yang berbeda:
| Wilayah | Unit Tekanan Umum |
|---|---|
| Amerika Utara | psi, inHg, inH₂O |
| Eropa | bar, Pa, mbar |
| Jepang | kgf/cm², MPa |
| Cina | MPa, bar |
| INGGRIS | bar, psi, Pa |
Pengukuran Tekanan dalam Dokumentasi
Apabila mendokumentasikan spesifikasi tekanan, sangat penting untuk menunjukkan secara jelas:
- Nilai numerik
- Unit pengukuran
- Apakah itu tekanan gauge (g) atau absolut (a)
Sebagai contoh:
- 6 bar_g (tekanan pengukur, 6 bar di atas atmosfer)
- 7,01 bar_a (tekanan absolut, tekanan total termasuk atmosfer)
Kesimpulan
Memahami fisika di balik silinder pneumatik - mulai dari perhitungan gaya Hukum Pascal hingga hubungan aliran-tekanan dan konversi satuan tekanan - sangat penting untuk desain sistem dan pemecahan masalah yang tepat. Prinsip-prinsip dasar ini membantu memastikan sistem pneumatik Anda memberikan kinerja yang diharapkan secara andal dan efisien.
Tanya Jawab Tentang Fisika dalam Sistem Pneumatik
Bagaimana cara menghitung keluaran gaya dari silinder pneumatik tanpa batang?
Untuk menghitung output gaya dari silinder pneumatik tanpa batang, kalikan tekanan operasi dengan area piston efektif (F = P × A). Sebagai contoh, silinder tanpa batang dengan lubang 50mm (luas 0,001963 m²) yang beroperasi pada 6 bar (600.000 Pa) akan menghasilkan sekitar 1.178 N gaya. Tidak seperti silinder tradisional, silinder tanpa batang biasanya memiliki area efektif yang sama di kedua arah.
Bagaimana cara menghitung keluaran gaya dari silinder pneumatik tanpa batang?
Untuk menghitung output gaya dari silinder pneumatik tanpa batang, kalikan tekanan operasi dengan area piston efektif (F = P × A). Sebagai contoh, silinder tanpa batang dengan lubang 50mm (luas 0,001963 m²) yang beroperasi pada 6 bar (600.000 Pa) akan menghasilkan sekitar 1.178 N gaya. Tidak seperti silinder tradisional, silinder tanpa batang biasanya memiliki area efektif yang sama di kedua arah.
Apa perbedaan antara tekanan pengukur dan tekanan absolut?
Tekanan pengukur (bar_g, psi_g) mengukur tekanan relatif terhadap tekanan atmosfer, dengan tekanan atmosfer nol. Tekanan absolut (bar_a, psi_a) mengukur tekanan relatif terhadap ruang hampa udara yang sempurna, yaitu nol. Untuk mengonversi dari pengukur ke tekanan absolut, tambahkan tekanan atmosfer (sekitar 1,01325 bar atau 14,7 psi) ke pembacaan pengukur.
Bagaimana aliran udara mempengaruhi kecepatan silinder?
Kecepatan silinder berbanding lurus dengan laju aliran udara dan berbanding terbalik dengan area piston (v = Q/A). Laju aliran yang tidak mencukupi karena jalur suplai yang terlalu kecil, alat kelengkapan yang membatasi, atau katup yang tidak memadai akan membatasi kecepatan silinder, berapa pun tekanannya. Sebagai contoh, laju aliran 20 liter/detik melalui silinder dengan luas piston 0,002 m² akan menghasilkan kecepatan 10 meter/detik.
Mengapa silinder pneumatik terkadang bergerak lebih lambat dari yang dihitung?
Silinder pneumatik dapat bergerak lebih lambat dari yang dihitung karena beberapa faktor: pembatasan pasokan udara yang menyebabkan penurunan tekanan, gesekan internal dari segel, beban mekanis yang melebihi perhitungan, kebocoran yang mengurangi tekanan efektif, atau efek suhu pada kepadatan udara. Selain itu, koefisien aliran katup sering kali membatasi laju aliran aktual yang tersedia untuk silinder.
Bagaimana cara mengonversi antara satuan tekanan yang berbeda untuk spesifikasi internasional?
Untuk mengkonversi antar satuan tekanan, gunakan faktor perkalian: 1 bar = 100.000 Pa = 0,1 MPa = 14,5038 psi = 1,01972 kgf/cm². Selalu pastikan apakah tekanan ditetapkan sebagai ukuran atau absolut, karena perbedaan ini dapat mempengaruhi perhitungan secara signifikan. Sebagai contoh, 6 bar_g sama dengan 7,01325 bar_a pada kondisi atmosfer standar.
Apa hubungan antara ukuran lubang silinder dan output gaya?
Hubungan antara ukuran lubang silinder dan output gaya adalah kuadratik-menggandakan diameter lubang akan meningkatkan output gaya sebanyak empat kali lipat (karena luas = π × r²). Sebagai contoh, pada tekanan operasi 6 bar, silinder lubang 40mm menghasilkan gaya sekitar 754 N, sedangkan silinder lubang 80mm menghasilkan sekitar 3.016 N, hampir empat kali lebih besar.
-
Memberikan penjelasan rinci tentang Hukum Pascal, prinsip dasar dalam mekanika fluida yang merupakan dasar untuk transmisi daya hidraulik dan pneumatik. ↩
-
Menawarkan definisi dan perbandingan yang jelas antara tekanan pengukur dan tekanan absolut, perbedaan penting untuk perhitungan teknik yang akurat karena tekanan pengukur relatif terhadap tekanan atmosfer. ↩
-
Menjelaskan penurunan dan penerapan hukum Poiseuille, yang menggambarkan penurunan tekanan fluida inkompresibel dan Newtonian yang mengalir melalui pipa silinder panjang dalam rezim laminar. ↩
-
Memberikan definisi teknis tentang Koefisien Aliran (Cv), pengukuran imperial yang menyediakan cara standar untuk membandingkan kapasitas aliran katup yang berbeda. ↩
-
Merinci fisika aliran tersendat, kondisi dinamika fluida yang membatasi laju aliran massa fluida yang dapat dimampatkan melalui pembatasan ketika kecepatannya mencapai kecepatan suara. ↩


