Hubungi kami

Bagaimana Kinematika Piston Mempengaruhi Kinerja Sistem Pneumatik Anda?

Bagaimana Kinematika Piston Mempengaruhi Kinerja Sistem Pneumatik Anda?
Kit Perakitan Silinder Pneumatik Kompak Seri CQ2
Kit Perakitan Silinder Pneumatik Kompak Seri CQ2

Apakah Anda mengalami masalah dengan kecepatan silinder pneumatik yang tidak konsisten atau dampak akhir langkah yang tidak terduga? Masalah umum ini sering kali berasal dari pemahaman yang buruk tentang kinematika piston. Banyak insinyur yang hanya berfokus pada kebutuhan gaya sambil mengabaikan parameter gerakan kritis yang menentukan kinerja sistem.

Kinematika piston1 secara langsung memengaruhi kinerja sistem pneumatik melalui hubungan tekanan-kecepatan, batas akselerasi, dan persyaratan bantalan. Memahami prinsip-prinsip ini memungkinkan para insinyur untuk mengukur komponen dengan benar, memprediksi profil gerakan aktual, dan mencegah kegagalan dini pada silinder tanpa batang dan aktuator pneumatik lainnya.

Selama lebih dari 15 tahun di Bepto bekerja dengan sistem pneumatik, saya telah melihat banyak kasus di mana pemahaman tentang prinsip-prinsip dasar ini telah membantu pelanggan memecahkan masalah kinerja yang terus-menerus dan memperpanjang usia peralatan hingga 3-5 kali lipat.

Daftar Isi

Tekanan Apa yang Sebenarnya Anda Butuhkan untuk Gerakan Kecepatan Konstan?

Banyak insinyur hanya menerapkan tekanan maksimum yang tersedia ke sistem pneumatik mereka, tetapi pendekatan ini tidak efisien dan dapat menyebabkan gerakan tersentak-sentak, keausan yang berlebihan, dan energi yang terbuang.

Tekanan yang diperlukan untuk gerakan kecepatan konstan dalam silinder pneumatik dihitung dengan menggunakan P = (F + Fr) / A, di mana P adalah tekanan, F adalah gaya beban eksternal, Fr adalah hambatan gesekan, dan A adalah area piston. Perhitungan ini memastikan pengoperasian yang lancar dan efisien tanpa tekanan berlebihan yang membuang energi dan mempercepat keausan komponen.

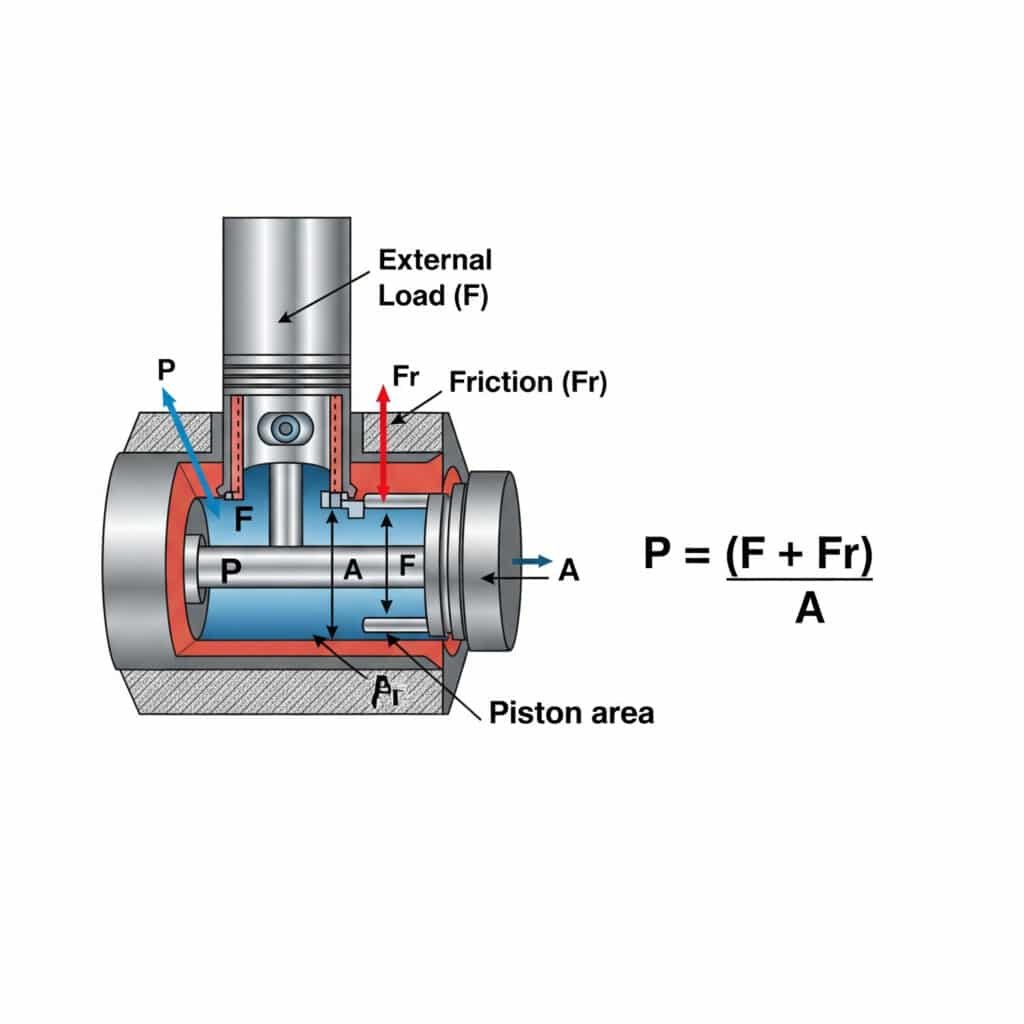
Diagram benda bebas teknis yang menjelaskan perhitungan tekanan untuk silinder pneumatik. Diagram ini menunjukkan penampang silinder yang mendorong blok, yang diberi label 'Beban Eksternal (F)'. Tanda panah menunjukkan 'Gesekan (Fr)' yang berlawanan. Tekanan di dalam diberi label 'P' dan bekerja pada 'Area Piston (A)'. Rumus 'P = (F + Fr)/A' ditampilkan dengan jelas, dengan panah yang menghubungkan setiap variabel ke gaya atau fitur yang sesuai dalam diagram.
Diagram perhitungan tekanan kecepatan konstan

Memahami persyaratan tekanan untuk gerakan kecepatan konstan memiliki implikasi praktis untuk desain dan pengoperasian sistem. Izinkan saya menguraikannya menjadi wawasan yang dapat ditindaklanjuti.

Faktor-faktor yang Mempengaruhi Persyaratan Tekanan untuk Kecepatan Konstan

Tekanan yang diperlukan untuk mempertahankan kecepatan konstan bergantung pada beberapa faktor:

FaktorDampak pada Kebutuhan TekananPertimbangan Praktis
Beban EksternalHubungan linier langsungBervariasi dengan orientasi dan kekuatan eksternal
GesekanMenambah tekanan yang dibutuhkanPerubahan dengan keausan seal dan pelumasan
Area PistonBerbanding terbalikLubang yang lebih besar = kebutuhan tekanan yang lebih rendah
Pembatasan Pasokan UdaraPenurunan tekanan pada saluran/katupKomponen ukuran untuk penurunan tekanan minimal
Tekanan BalikMenentang gerakanPertimbangkan kapasitas aliran gas buang

Menghitung Tekanan Minimum untuk Gerakan Stabil

Untuk menentukan tekanan minimum yang diperlukan untuk gerakan yang stabil:

  1. Hitung gaya yang diperlukan untuk mengatasi beban eksternal
  2. Tambahkan gaya gesekan (biasanya 3-20% gaya maksimum)
  3. Bagilah dengan luas piston efektif
  4. Tambahkan faktor stabilitas (biasanya 10-30%)

Misalnya, pada silinder tanpa batang bore 40mm dengan beban 10kg dan gesekan 15%:

ParameterPerhitunganHasil
Kekuatan Beban10kg × 9,81m / s²98.1N
Gaya Gesekan15% kekuatan maksimal pada 6 bar~45N
Total Kekuatan98,1N + 45N143.1N
Area Pistonπ × (0,02m)²0.00126m²
Tekanan Minimum143,1N ÷ 0,00126m²113.571 Pa (1,14 bar)
Dengan Faktor Stabilitas 20%1,14 bar × 1,21,37 bar

Aplikasi Dunia Nyata: Penghematan Energi Melalui Optimalisasi Tekanan

Tahun lalu, saya bekerja dengan Robert, seorang insinyur produksi di sebuah pabrik furnitur di Michigan. Jalur perakitan otomatisnya menggunakan silinder tanpa batang yang beroperasi pada tekanan suplai 6 bar penuh, berapa pun bebannya.

Setelah menganalisis aplikasinya, kami menentukan bahwa sebagian besar gerakan hanya memerlukan 2,5-3 bar untuk pengoperasian yang stabil. Dengan menginstal regulator tekanan proporsionalkami mengurangi konsumsi udara sebesar 40% dengan tetap mempertahankan waktu siklus yang sama. Hal ini menghemat sekitar $12.000 per tahun dalam biaya energi sekaligus mengurangi keausan seal dan memperpanjang interval perawatan.

Hubungan Kecepatan-Tekanan dalam Sistem Nyata

Dalam praktiknya, hubungan antara tekanan dan kecepatan tidak linier sempurna karena:

  1. Pembatasan aliran: Ukuran katup dan port mempengaruhi kecepatan maksimum yang dapat dicapai
  2. Efek kompresibilitas: Udara bersifat kompresibel, menyebabkan kelambatan akselerasi
  3. Fenomena selip tongkat: Karakteristik gesekan berubah dengan kecepatan
  4. Efek inersia: Akselerasi massa membutuhkan gaya/tekanan tambahan

Bagaimana Anda Menghitung Akselerasi Maksimum yang Mungkin Terjadi pada Silinder Pneumatik?

Memahami batas akselerasi sangat penting untuk mencegah guncangan berlebihan, getaran, dan kegagalan komponen dini dalam sistem pneumatik.

Akselerasi maksimum yang mungkin terjadi pada silinder pneumatik dihitung dengan menggunakan a = (P × A - F - Fr) / m, di mana a adalah akselerasi, P adalah tekanan, A adalah luas piston, F adalah beban eksternal, Fr adalah hambatan gesekan, dan m adalah massa yang bergerak. Persamaan ini mendefinisikan batas fisik seberapa cepat aktuator pneumatik dapat memulai atau menghentikan gerakan.

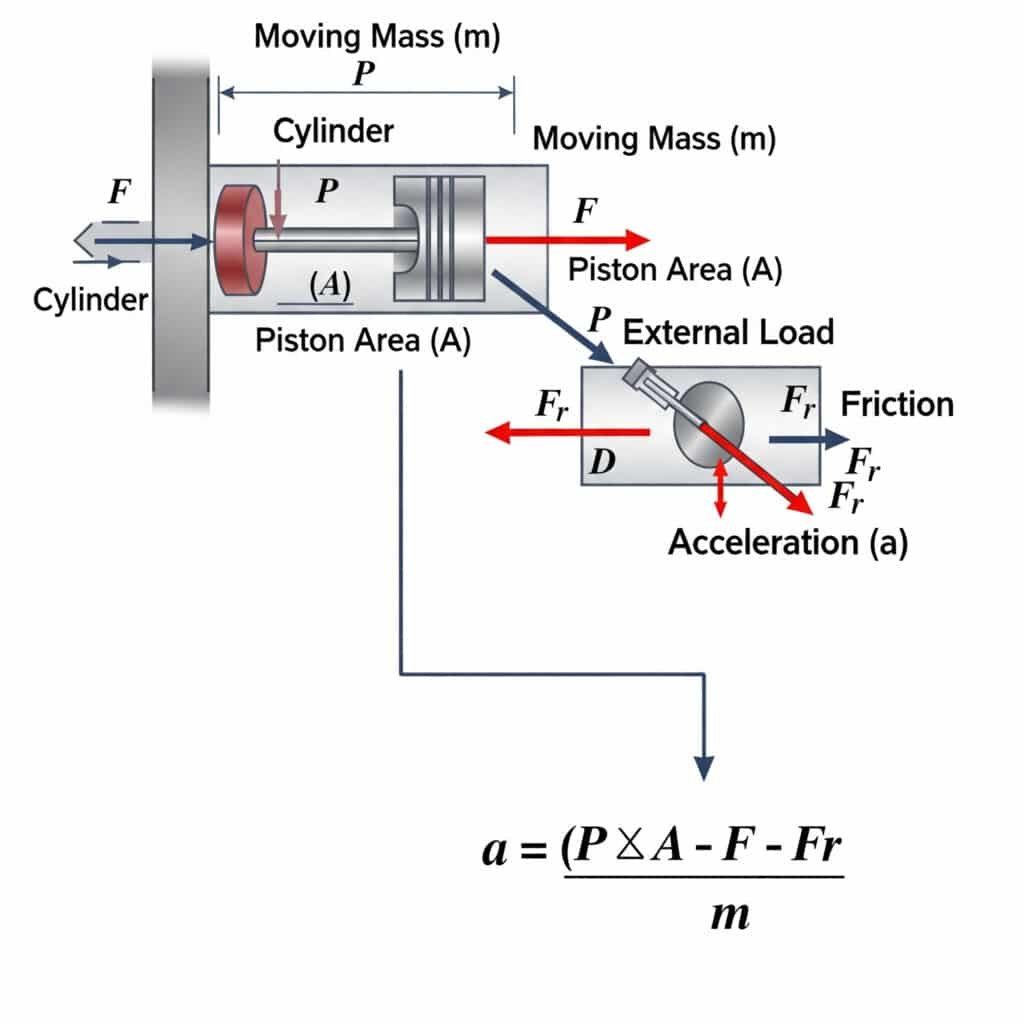
Diagram benda bebas teknis yang menjelaskan perhitungan percepatan silinder pneumatik. Ilustrasi menunjukkan sebuah silinder yang mendorong sebuah blok, yang diberi label 'Massa Bergerak (m)'. Panah besar menunjukkan gaya pendorong yang dihasilkan oleh 'Tekanan (P)' pada 'Area Piston (A)'. Berlawanan dengan ini adalah dua panah yang lebih kecil berlabel 'Beban Eksternal (F)' dan 'Gesekan (Fr)'. Panah besar menunjukkan 'Akselerasi (a)' yang dihasilkan. Rumus 'a = (P × A - F - Fr) / m' ditampilkan dengan jelas, dengan setiap variabel yang terhubung ke elemen yang sesuai dalam diagram.
Diagram penurunan batas percepatan

Batas akselerasi teoretis memiliki implikasi praktis yang signifikan untuk desain sistem dan pemilihan komponen.

Penurunan Persamaan Batas Percepatan

Persamaan batas percepatan berasal dari Hukum Kedua Newton2 (F = ma):

  1. Gaya bersih yang tersedia untuk akselerasi adalah: Fnet = Ftekanan - Fbeban - Fgaya gesek
  2. Tekanan F = P × A
  3. Oleh karena itu: a = Fnet/m = (P × A - F - Fr) / m

Batas Akselerasi Praktis untuk Berbagai Jenis Silinder

Desain silinder yang berbeda memiliki batas akselerasi praktis yang berbeda:

Jenis SilinderAkselerasi Maksimum KhasFaktor Pembatas
Silinder batang standar10-15 m/s²Tekuk batang, menahan beban
Silinder tanpa batang (magnetik)8-12 m/s²Kekuatan kopling magnetik
Silinder tanpa batang (mekanis)15-25 m/s²Desain segel/bantalan, gesekan internal
Silinder pemandu20-30 m/s²Kekakuan sistem pemandu, daya dukung
Silinder benturan50-100+ m/s²Dirancang khusus untuk akselerasi tinggi

Pertimbangan Massa dalam Perhitungan Percepatan

Ketika menghitung percepatan, sangat penting untuk menyertakan semua massa yang bergerak:

  1. Perakitan piston: Termasuk piston, seal, dan elemen penghubung
  2. Massa beban: Beban eksternal sedang dipindahkan
  3. Massa efektif udara yang bergerak: Sering kali dapat diabaikan tetapi relevan dalam aplikasi kecepatan tinggi
  4. Menambah massa karena pemasangan komponen: Tanda kurung, sensor, dll.

Saya pernah membantu seorang pelanggan di Prancis yang mengalami kegagalan misterius pada sistem silinder tanpa batangnya. Silinder tersebut memiliki ukuran yang tepat untuk beban 15kg yang dinyatakan, tetapi secara konsisten mengalami kegagalan setelah beberapa ribu siklus.

Setelah menyelidikinya, kami menemukan bahwa ia lalai memperhitungkan massa 12kg dari pelat dudukan dan perlengkapannya. Massa yang bergerak sebenarnya hampir dua kali lipat dari yang ia perhitungkan, menyebabkan gaya akselerasi yang melebihi batas desain silinder. Setelah meningkatkan ke silinder yang lebih besar, kegagalan berhenti sepenuhnya.

Metode Kontrol Akselerasi

Untuk mengontrol akselerasi dalam batas aman:

  1. Katup kontrol aliran: Batasi laju aliran selama gerakan awal
  2. Katup proporsional: Menyediakan peningkatan tekanan yang terkontrol
  3. Akselerasi multi-tahap: Gunakan peningkatan tekanan bertahap
  4. Peredaman mekanis: Menambahkan peredam kejut eksternal
  5. Kontrol elektronik: Gunakan sistem servo-pneumatik3 dengan umpan balik akselerasi

Mengapa Waktu Bantalan Penting dan Bagaimana Cara Menghitungnya?

Bantalan akhir langkah yang tepat sangat penting untuk mencegah kerusakan akibat benturan, mengurangi kebisingan, dan memperpanjang usia silinder pneumatik. Memahami waktu bantalan membantu para insinyur merancang sistem yang menyeimbangkan waktu siklus dengan umur komponen.

Waktu bantalan pada silinder pneumatik dihitung dengan menggunakan persamaan t = √(2s/a), di mana t adalah waktu, s adalah panjang langkah bantalan, dan a adalah perlambatan. Waktu ini menunjukkan berapa lama waktu yang diperlukan untuk memperlambat massa yang bergerak dengan aman sebelum tumbukan, yang sangat penting untuk mencegah kerusakan pada silinder dan komponen yang terpasang.

Infografis teknis yang menjelaskan perhitungan waktu bantalan pneumatik. Infografis ini menunjukkan penampang piston yang diperbesar yang memasuki bantalan di ujung silinder. Garis dimensi menunjukkan 'Langkah Bantalan (s),' sementara panah besar yang berlawanan menunjukkan 'Perlambatan (a). Ikon stopwatch memvisualisasikan 'Waktu Bantalan (t)'. Rumus 't = √(2s/a)' ditampilkan dengan jelas, dengan panah yang menghubungkan setiap variabel ke elemen yang sesuai dalam diagram.
Diagram penurunan batas percepatan

Mari kita jelajahi aspek praktis dari perhitungan waktu bantalan dan implikasinya untuk desain sistem.

Fisika di Balik Bantalan Pneumatik

Bantalan pneumatik bekerja melalui kompresi udara yang terkendali dan pembuangan yang terbatas:

  1. Saat piston memasuki ruang bantalan, jalur pembuangan dibatasi
  2. Udara yang terperangkap memampatkan, menciptakan tekanan balik yang meningkat
  3. Tekanan balik ini menciptakan gaya berlawanan yang memperlambat piston
  4. Profil perlambatan tergantung pada desain dan penyesuaian bantalan

Menghitung Waktu Bantalan yang Optimal

Waktu bantalan yang optimal menyeimbangkan pencegahan benturan dengan efisiensi waktu siklus:

ParameterFormulaContoh
Jarak BantalanBerdasarkan desain silinder15mm (tipikal untuk lubang 40mm)
Perlambatan yang Diperlukana = v² / (2s)Untuk v = 0,5 m/s, s = 15 mm: a = 8,33 m/s²
Waktu Bantalant = √(2s/a)t = √(2 × 0,015 / 8,33) = 0,06 detik
Peningkatan TekananP = P₀ (V₀/V) ^ γTergantung pada geometri ruang bantalan

Faktor-faktor yang Mempengaruhi Kinerja Bantalan

Beberapa faktor memengaruhi kinerja bantalan yang sebenarnya:

  1. Desain segel bantalan: Mempengaruhi kebocoran udara selama bantalan
  2. Penyetelan katup jarum: Mengontrol laju pembatasan knalpot
  3. Massa yang bergerak: Beban yang lebih berat membutuhkan waktu bantalan yang lebih lama
  4. Kecepatan pendekatan: Kecepatan yang lebih tinggi membutuhkan jarak bantalan yang lebih panjang
  5. Tekanan operasi: Mempengaruhi kekuatan kontra maksimum yang tersedia

Jenis Bantalan dan Aplikasinya

Mekanisme bantalan yang berbeda sesuai untuk aplikasi yang berbeda:

Jenis BantalanKarakteristikAplikasi Terbaik
Bantalan tetapSederhana, tidak dapat disesuaikanBeban ringan, pengoperasian yang konsisten
Bantalan yang dapat disesuaikanDapat disetel dengan katup jarumBeban yang bervariasi, aplikasi yang fleksibel
Bantalan yang dapat menyesuaikan sendiriBeradaptasi dengan kondisi yang berbedaMengubah kecepatan dan beban
Peredam kejut eksternalPenyerapan energi yang tinggiBeban berat, kecepatan tinggi
Bantalan elektronikPerlambatan yang terkontrol dengan tepatSistem servo-pneumatik

Studi Kasus: Mengoptimalkan Bantalan dalam Aplikasi Siklus Tinggi

Baru-baru ini saya bekerja dengan Thomas, seorang insinyur desain di produsen komponen otomotif di Jerman. Lini perakitannya menggunakan silinder tanpa batang yang beroperasi pada 45 siklus per menit, tetapi sering mengalami kegagalan seal dan kerusakan braket pemasangan.

Analisis mengungkapkan bahwa waktu bantalan terlalu singkat untuk massa yang bergerak, menyebabkan gaya tumbukan hampir 3G pada setiap akhir langkah. Dengan meningkatkan langkah bantalan dari 12mm ke 20mm dan mengoptimalkan pengaturan katup jarum, kami memperpanjang waktu bantalan dari 0,04 detik ke 0,07 detik.

Perubahan yang tampaknya kecil ini mengurangi gaya benturan hingga lebih dari 60%, menghilangkan kerusakan braket sepenuhnya, dan memperpanjang masa pakai seal dari 3 bulan menjadi lebih dari satu tahun-semuanya sambil mempertahankan waktu siklus yang diperlukan.

Prosedur Penyesuaian Bantalan Praktis

Untuk performa bantalan yang optimal pada silinder tanpa batang:

  1. Mulailah dengan katup bantalan terbuka penuh (pembatasan minimum)
  2. Tutup katup bantalan secara bertahap hingga deselerasi yang mulus tercapai
  3. Uji dengan beban minimum dan maksimum yang diharapkan
  4. Memverifikasi kinerja bantalan di seluruh rentang kecepatan penuh
  5. Dengarkan suara benturan yang mengindikasikan bantalan yang tidak memadai
  6. Mengukur waktu perlambatan aktual untuk mengonfirmasi perhitungan

Kesimpulan

Memahami prinsip-prinsip kinematika piston - mulai dari persyaratan tekanan untuk kecepatan konstan hingga batas akselerasi dan perhitungan waktu bantalan - sangat penting untuk merancang sistem pneumatik yang efisien dan andal. Dengan menerapkan prinsip-prinsip ini pada aplikasi silinder tanpa batang, Anda dapat mengoptimalkan kinerja, mengurangi konsumsi energi, dan memperpanjang usia komponen secara signifikan.

Tanya Jawab Tentang Kinematika Piston dalam Sistem Pneumatik

Tekanan apa yang saya perlukan untuk kecepatan silinder tertentu?

Tekanan yang dibutuhkan tergantung pada beban, gesekan, dan area silinder. Hitunglah dengan menggunakan P = (F + Fr)/A, di mana F adalah gaya beban eksternal, Fr adalah hambatan gesekan, dan A adalah area piston. Untuk silinder tanpa batang yang menggerakkan beban 10kg secara horizontal, Anda memerlukan sekitar 1,5-2 bar untuk gerakan yang stabil pada kecepatan sedang.

Seberapa cepat silinder pneumatik dapat berakselerasi?

Akselerasi maksimum silinder pneumatik dihitung dengan menggunakan a = (P × A - F - Fr) / m. Silinder tanpa batang yang umum dapat mencapai akselerasi 10-25 m/s², tergantung pada desainnya. Ini berarti mencapai kecepatan 0,5 m/s dalam waktu sekitar 20-50 milidetik dalam kondisi optimal.

Faktor-faktor apa saja yang membatasi kecepatan maksimum silinder tanpa batang?

Kecepatan maksimum dibatasi oleh kapasitas aliran katup, volume pasokan udara, ukuran port, kemampuan bantalan, dan desain seal. Sebagian besar silinder tanpa batang standar dirancang untuk kecepatan maksimum 0,8-1,5 m/dtk, meskipun desain kecepatan tinggi khusus dapat mencapai 2-3 m/dtk.

Bagaimana cara menghitung bantalan yang tepat untuk aplikasi saya?

Hitung bantalan yang tepat dengan menentukan energi kinetik (KE = ½mv²) dari beban yang bergerak dan pastikan sistem bantalan Anda dapat menyerap energi ini. Waktu peredaman harus dihitung dengan menggunakan t = √(2s/a), di mana s adalah jarak peredaman dan a adalah tingkat perlambatan yang diinginkan.

Apa yang terjadi jika silinder pneumatik saya berakselerasi terlalu cepat?

Akselerasi yang berlebihan dapat menyebabkan tekanan mekanis pada komponen pemasangan, keausan seal prematur, peningkatan getaran dan kebisingan, potensi pergeseran beban atau kerusakan, dan berkurangnya presisi sistem. Hal ini juga dapat menyebabkan gerakan tersentak-sentak yang memengaruhi kualitas produk dalam aplikasi presisi.

Bagaimana orientasi beban memengaruhi tekanan yang diperlukan untuk pergerakan?

Orientasi beban secara signifikan memengaruhi kebutuhan tekanan. Beban vertikal yang bergerak melawan gravitasi membutuhkan tekanan tambahan untuk mengatasi gaya gravitasi (P = F/A + Fg/A + Fr/A). Beban horizontal hanya perlu mengatasi gesekan dan inersia. Beban miring berada di antara kedua titik ekstrem ini berdasarkan sinus sudut.

  1. Memberikan penjelasan dasar tentang kinematika, cabang ilmu mekanika yang menggambarkan gerakan benda tanpa mempertimbangkan gaya yang menyebabkan gerakan tersebut.
    sinyal input elektronik, memungkinkan kontrol pneumatik tingkat lanjut. ↩

  2. Detail Hukum Kedua Newton (F=ma), prinsip dasar fisika yang menghubungkan gaya yang bekerja pada sebuah objek dengan massa dan percepatannya, yang menjadi dasar semua perhitungan dinamis. ↩

  3. Menjelaskan tentang servo-pneumatik, teknologi kontrol canggih yang memadukan kekuatan pneumatik dengan presisi kontrol elektronik loop tertutup untuk mencapai profil posisi dan gerakan yang sangat akurat. ↩

Terkait

Chuck Bepto

Halo, saya Chuck, seorang ahli senior dengan pengalaman 15 tahun di industri pneumatik. Di Bepto Pneumatic, saya fokus untuk memberikan solusi pneumatik berkualitas tinggi yang dibuat khusus untuk klien kami. Keahlian saya meliputi otomasi industri, desain dan integrasi sistem pneumatik, serta aplikasi dan pengoptimalan komponen utama. Jika Anda memiliki pertanyaan atau ingin mendiskusikan kebutuhan proyek Anda, jangan ragu untuk menghubungi saya di chuck@bepto.com.

Daftar Isi
Logo Bepto

Dapatkan Lebih Banyak Manfaat Sejak Mengirimkan Formulir Info