
Apakah Anda pernah menyentuh silinder pneumatik setelah beroperasi terus menerus dan terkejut dengan betapa panasnya rasanya? Panas tersebut bukan hanya ketidaknyamanan-ini merupakan energi yang terbuang, efisiensi yang berkurang, dan potensi masalah keandalan yang dapat merugikan operasi Anda hingga ribuan kali lipat.
Perpindahan panas dalam sistem pneumatik terjadi melalui tiga mekanisme: konduksi melalui bahan komponen, konveksi antara permukaan dan udara, dan radiasi dari permukaan yang panas. Memahami dan mengoptimalkan prinsip-prinsip ini dapat mengurangi suhu pengoperasian sebesar 15-30%, memperpanjang usia komponen hingga 40%, dan meningkatkan efisiensi energi sebesar 5-15%.
Bulan lalu, saya berkonsultasi dengan sebuah pabrik pengolahan makanan di Georgia di mana silinder tanpa batang mereka mengalami kegagalan setiap 3-4 bulan karena masalah termal. Tim pemeliharaan mereka hanya mengganti komponen tanpa mengatasi akar penyebabnya. Dengan menerapkan prinsip-prinsip perpindahan panas yang tepat, kami mengurangi suhu operasi hingga 22°C dan memperpanjang usia komponen hingga lebih dari satu tahun. Izinkan saya menunjukkan kepada Anda bagaimana kami melakukannya-dan bagaimana Anda dapat menerapkan prinsip-prinsip yang sama pada sistem Anda.
Daftar Isi
- Perhitungan Koefisien Konduksi: Bagaimana Panas Bergerak Melalui Komponen Anda?
- Metode Peningkatan Konveksi: Teknik Apa yang Memaksimalkan Perpindahan Panas dari Udara ke Permukaan?
- Model Efisiensi Radiasi: Kapan Radiasi Termal Penting dalam Sistem Pneumatik?
- Kesimpulan
- Tanya Jawab Tentang Perpindahan Panas dalam Sistem Pneumatik
Perhitungan Koefisien Konduksi: Bagaimana Panas Bergerak Melalui Komponen Anda?
Konduksi adalah mekanisme perpindahan panas utama di dalam komponen pneumatik padat. Memahami cara menghitung dan mengoptimalkan koefisien konduksi sangat penting untuk mengelola suhu sistem.
Koefisien konduksi panas dapat dihitung dengan menggunakan Hukum Fourier1q = -k (dT/dx), di mana q adalah fluks panas (W/m²), k adalah konduktivitas termal (W/m-K), dan dT/dx adalah gradien suhu. Untuk komponen pneumatik, konduksi yang efektif bergantung pada pemilihan material, kualitas antarmuka, dan faktor geometris yang memengaruhi panjang jalur panas dan luas penampang.
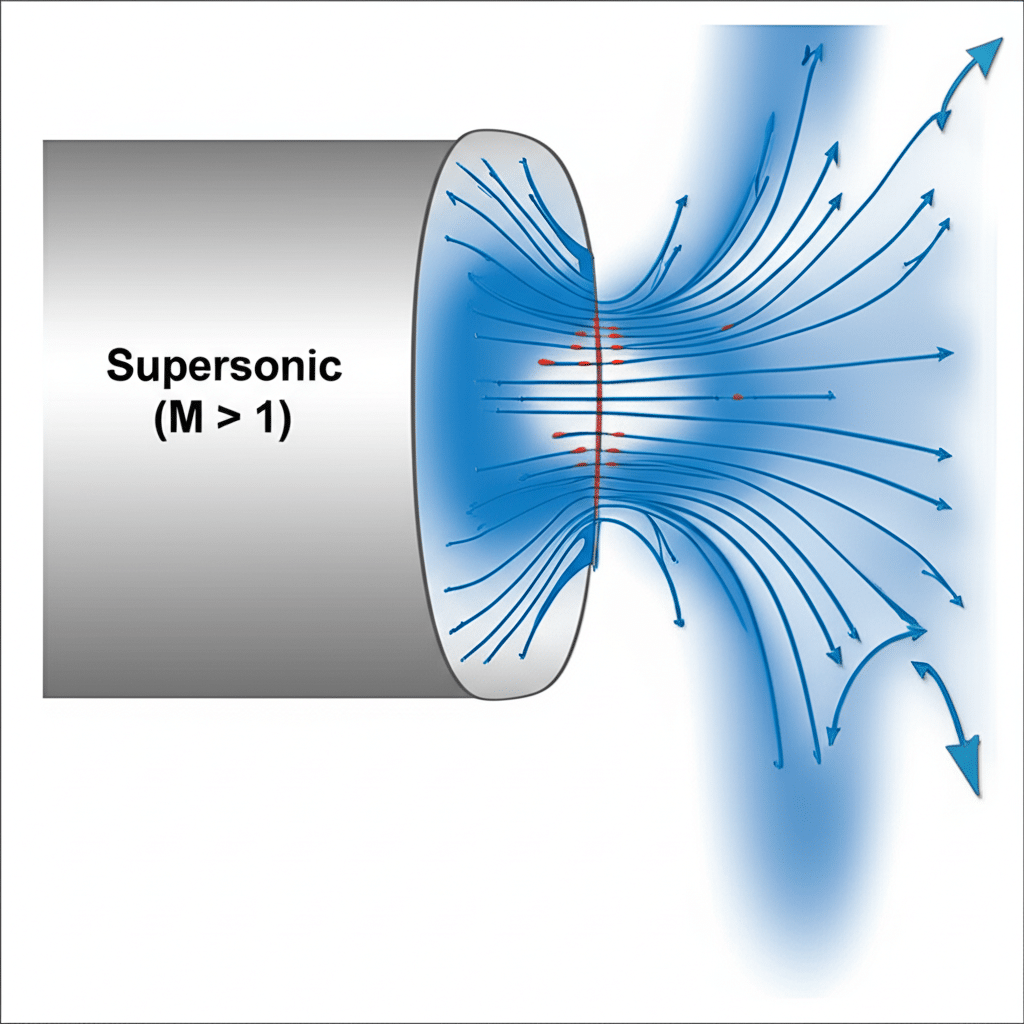
Saya ingat pernah memecahkan masalah pada lini produksi di Tennessee di mana bantalan silinder tanpa batang mengalami kerusakan sebelum waktunya. Tim pemeliharaan telah mencoba beberapa pelumas tanpa hasil. Ketika kami menganalisis jalur konduksi, kami menemukan hambatan termal pada antarmuka bearing-rumah. Dengan meningkatkan permukaan akhir dan menerapkan senyawa konduktif termal, kami meningkatkan koefisien konduksi efektif sebesar 340% dan menghilangkan kegagalan sepenuhnya.
Persamaan Konduksi Fundamental
Mari kita uraikan persamaan kunci untuk menghitung konduksi dalam komponen pneumatik:
Hukum Fourier untuk Konduksi Panas
Persamaan dasar yang mengatur konduksi panas adalah:
q = -k (dT/dx)
Dimana:
- q = Fluks panas (W/m²)
- k = Konduktivitas termal (W/m-K)
- dT/dx = Gradien suhu (K/m)
Untuk kasus satu dimensi sederhana dengan penampang yang konstan:
Q = kA (T₁ - T₂) / L
Dimana:
- Q = Laju perpindahan panas (W)
- A = Luas penampang melintang (m²)
- T₁, T₂ = Suhu di setiap ujung (K)
- L = Panjang jalur panas (m)
Konsep Ketahanan Termal
Untuk geometri yang kompleks, pendekatan resistensi termal sering kali lebih praktis:
R = L/(kA)
Dimana:
- R = Resistensi termal (K/W)
Untuk sistem dengan beberapa komponen secara seri:
Rtotal = R₁ + R₂ + R₃ + ... + Rₙ
Dan laju perpindahan panas menjadi:
Q = ΔT/Rtotal
Perbandingan Konduktivitas Termal Material
| Bahan | Konduktivitas Termal (W/m-K) | Konduktivitas Relatif | Aplikasi Umum |
|---|---|---|---|
| Aluminium | 205-250 | Tinggi | Silinder, heat sink |
| Baja | 36-54 | Sedang | Komponen struktural |
| Baja tahan karat | 14-16 | Rendah-Sedang | Lingkungan korosif |
| Perunggu | 26-50 | Sedang | Bantalan, bushing |
| PTFE | 0.25 | Sangat Rendah | Segel, bantalan |
| Karet Nitril | 0.13 | Sangat Rendah | Cincin-O, segel |
| Udara (diam) | 0.026 | Sangat Rendah | Pengisi celah |
| Pasta Termal | 3-8 | Rendah | Bahan antarmuka |
Resistensi Kontak dalam Rakitan Pneumatik
Pada antarmuka antar komponen, resistansi kontak secara signifikan memengaruhi perpindahan panas:
Rkontak = 1/(hc × A)
Dimana:
- hc = Koefisien kontak (W/m²-K)
- A = Area kontak (m²)
Faktor-faktor yang mempengaruhi resistensi kontak meliputi:
- Kekasaran Permukaan: Permukaan yang lebih kasar memiliki area kontak yang lebih sedikit
- Tekanan Kontak: Tekanan yang lebih tinggi meningkatkan area kontak yang efektif
- Bahan Antarmuka: Senyawa termal mengisi celah udara
- Kebersihan Permukaan: Kontaminan dapat meningkatkan resistensi
Studi Kasus: Pengoptimalan Termal Silinder Tanpa Batang
Untuk silinder tanpa batang magnetik yang mengalami masalah termal:
| Komponen | Desain Asli | Desain yang Dioptimalkan | Peningkatan |
|---|---|---|---|
| Badan Silinder | Aluminium Anodized | Bahan yang sama, hasil akhir yang lebih baik | 15% konduksi yang lebih baik |
| Antarmuka Bantalan | Kontak logam ke logam | Menambahkan senyawa termal | 340% konduksi yang lebih baik |
| Braket Pemasangan | Baja yang dicat | Aluminium polos | 280% konduksi yang lebih baik |
| Ketahanan Termal Keseluruhan | 2,8 K/W | 0,7 K / W | Pengurangan 75% |
| Suhu Operasi | 78°C | 56°C | Pengurangan 22°C |
| Umur Komponen | 4 bulan | > 12 bulan | 3 × peningkatan |
Teknik Pengoptimalan Konduksi Praktis
Berdasarkan pengalaman saya dengan ratusan sistem pneumatik, berikut ini adalah pendekatan yang paling efektif untuk meningkatkan konduksi:
Pengoptimalan Antarmuka
- Finishing Permukaan: Meningkatkan kehalusan permukaan perkawinan hingga Ra 0,4-0,8 μm
- Bahan Antarmuka Termal2: Terapkan senyawa yang sesuai (3-8 W/m-K)
- Torsi Pengikat: Pastikan pengencangan yang tepat untuk tekanan kontak yang optimal
- Kebersihan: Bersihkan semua oli dan kontaminan sebelum perakitan
Strategi Pemilihan Bahan
- Jalur Panas Kritis: Gunakan bahan dengan konduktivitas tinggi (aluminium, tembaga)
- Istirahat Termal: Sengaja menggunakan bahan dengan konduktivitas rendah untuk mengisolasi panas
- Pendekatan Komposit: Memadukan bahan untuk kinerja/biaya yang optimal
- Bahan Anisotropik: Memanfaatkan konduktivitas terarah jika diperlukan
Pengoptimalan Geometris
- Panjang Jalur Panas: Meminimalkan jarak antara sumber panas dan pendingin
- Luas Penampang Melintang: Memaksimalkan area yang tegak lurus terhadap aliran panas
- Hambatan Termal: Mengidentifikasi dan menghilangkan penyempitan pada jalur panas
- Jalur yang berlebihan: Membuat beberapa rute konduksi paralel
Metode Peningkatan Konveksi: Teknik Apa yang Memaksimalkan Perpindahan Panas dari Udara ke Permukaan?
Konveksi sering kali menjadi faktor pembatas dalam pendinginan sistem pneumatik. Meningkatkan perpindahan panas konvektif dapat secara dramatis meningkatkan manajemen termal dan kinerja sistem.
Perpindahan panas konvektif mengikuti Hukum Pendinginan Newton3: Q = hA(Ts-T∞), di mana h adalah koefisien konveksi (W/m²-K), A adalah luas permukaan, dan (Ts-T∞) adalah perbedaan temperatur antara permukaan dan fluida. Metode peningkatan termasuk meningkatkan luas permukaan melalui sirip, meningkatkan kecepatan fluida dengan aliran udara terarah, dan mengoptimalkan karakteristik permukaan untuk meningkatkan lapisan batas turbulen.
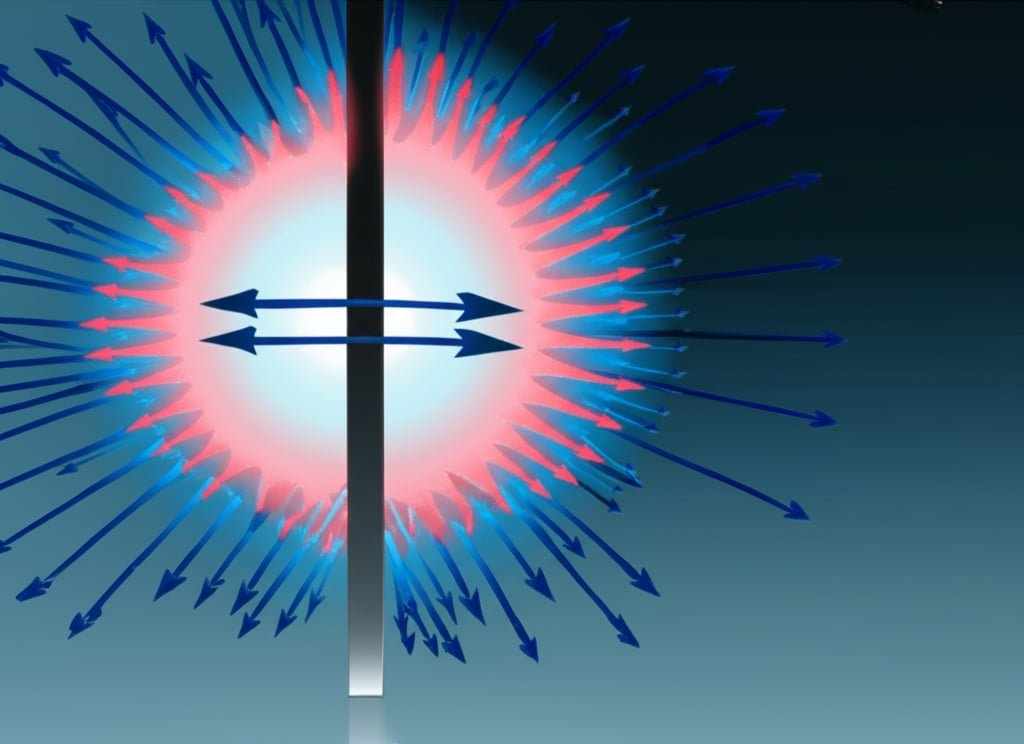
Selama audit efisiensi energi di fasilitas pengemasan di Arizona, saya menemukan sistem pneumatik yang beroperasi di lingkungan sekitar 43°C. Silinder tanpa batangnya mengalami panas berlebih meskipun telah memenuhi semua persyaratan pemeliharaan. Dengan menerapkan peningkatan konveksi yang ditargetkan-menambahkan sirip aluminium kecil dan kipas berdaya rendah-kami meningkatkan koefisien konveksi sebesar 450%. Hal ini mengurangi suhu pengoperasian dari tingkat berbahaya ke dalam spesifikasi tanpa modifikasi sistem yang besar.
Dasar-Dasar Perpindahan Panas Konveksi
Persamaan dasar yang mengatur perpindahan panas konvektif adalah:
Q = hA(Ts-T∞)
Dimana:
- Q = Laju perpindahan panas (W)
- h = Koefisien konveksi (W/m²-K)
- A = Luas permukaan (m²)
- Ts = Suhu permukaan (K)
- T∞ = Suhu fluida (udara) (K)
Koefisien konveksi h bergantung pada beberapa faktor:
- Sifat fluida (densitas, viskositas, konduktivitas termal)
- Karakteristik aliran (kecepatan, turbulensi)
- Geometri dan orientasi permukaan
- Rezim aliran (konveksi alami vs. konveksi paksa)
Konveksi Alami vs. Konveksi Paksa
| Parameter | Konveksi Alami | Konveksi Paksa | Implikasi |
|---|---|---|---|
| Nilai h yang khas | 5-25 W/m²-K | 25-250 W/m²-K | Konveksi paksa bisa 10 kali lebih efektif |
| Kekuatan Pendorong | Daya apung (perbedaan suhu) | Tekanan eksternal (kipas angin, blower) | Konveksi paksa tidak terlalu bergantung pada suhu |
| Pola Aliran | Aliran vertikal di sepanjang permukaan | Arah berdasarkan mekanisme pemaksaan | Aliran paksa dapat dioptimalkan untuk komponen tertentu |
| Keandalan | Pasif, selalu hadir | Membutuhkan daya dan perawatan | Konveksi alami memberikan pendinginan dasar |
| Persyaratan Ruang | Membutuhkan ruang bebas untuk sirkulasi udara | Membutuhkan ruang untuk penggerak udara dan saluran udara | Sistem yang dipaksakan membutuhkan lebih banyak perencanaan |
Teknik Peningkatan Konveksi
Penambahan Luas Permukaan
Meningkatkan luas permukaan yang efektif melalui:
Sirip dan Permukaan yang Diperluas
- Sirip pin: Aliran udara omnidirectional, peningkatan area 150-300%
- Sirip piring: Aliran udara terarah, peningkatan area 200-500%
- Permukaan bergelombang: Peningkatan sedang, peningkatan area 50-150%Pengasaran Permukaan
- Tekstur mikro: Peningkatan area efektif 5-15%
- Permukaan berlesung pipit: peningkatan 10-30% ditambah efek lapisan batas
- Pola beralur: Peningkatan 15-40% dengan manfaat terarah
Manipulasi Aliran
Meningkatkan karakteristik aliran udara melalui:
Sistem Udara Paksa
- Kipas: Aliran udara terarah, peningkatan 200-600% jam
- Blower: Aliran tekanan tinggi, peningkatan 300-800% jam
- Semburan udara terkompresi: Pendinginan yang ditargetkan, peningkatan h lokal 400-1000%Pengoptimalan Jalur Aliran
- Penyekat: Mengarahkan udara ke komponen penting
- Efek Venturi: Mempercepat udara di atas permukaan tertentu
- Generator pusaran: Menciptakan turbulensi untuk gangguan lapisan batas
Modifikasi Permukaan
Mengubah sifat permukaan untuk meningkatkan konveksi:
Perawatan Emisivitas
- Oksida hitam: Meningkatkan emisivitas hingga 0,7-0,9
- Anodisasi: Emisivitas terkendali dari 0,4-0,9
- Cat dan pelapis: Emisivitas yang dapat disesuaikan hingga 0,98Kontrol Kebasahan
- Pelapis hidrofilik: Meningkatkan pendinginan cairan
- Permukaan hidrofobik: Mencegah masalah kondensasi
- Pembasahan berpola: Aliran kondensat terarah
Contoh Implementasi Praktis
Untuk silinder pneumatik tanpa batang yang beroperasi di lingkungan bersuhu tinggi:
| Metode Peningkatan | Implementasi | h Peningkatan | Pengurangan Suhu |
|---|---|---|---|
| Sirip Pin (6mm) | Sirip clip-on aluminium, jarak 10mm | 180% | 12°C |
| Aliran Udara Terarah | 80mm, kipas DC 2W dengan kecepatan 1,5 m/s | 320% | 18°C |
| Perawatan Permukaan | Anodisasi hitam | 40% | 3°C |
| Pendekatan Gabungan | Semua metode terintegrasi | 450% | 24°C |
Korelasi Bilangan Nusselt untuk Perhitungan Desain
Untuk perhitungan teknik, metode Angka Nusselt4 (Nu) memberikan pendekatan tanpa dimensi pada konveksi:
Nu = hL/k
Dimana:
- L = Panjang karakteristik
- k = Konduktivitas termal fluida
Untuk konveksi paksa di atas pelat datar:
Nu = 0,664Re^(1/2) Pr^(1/3) (aliran laminar)
Nu = 0,037Re^(4/5) Pr^(1/3) (aliran turbulen)
Dimana:
- Re = Bilangan Reynolds (kecepatan × panjang × densitas / viskositas)
- Pr = Bilangan Prandtl (panas spesifik × viskositas / konduktivitas termal)
Korelasi ini memungkinkan para insinyur untuk memprediksi koefisien konveksi untuk konfigurasi yang berbeda dan mengoptimalkan strategi pendinginan yang sesuai.
Model Efisiensi Radiasi: Kapan Radiasi Termal Penting dalam Sistem Pneumatik?
Radiasi sering kali diabaikan dalam manajemen termal sistem pneumatik, tetapi radiasi dapat menyumbang 15-30% dari total perpindahan panas dalam banyak aplikasi. Memahami kapan dan bagaimana mengoptimalkan perpindahan panas radiatif sangat penting untuk manajemen termal yang komprehensif.
Perpindahan panas radiasi mengikuti Hukum Stefan-Boltzmann5: Q = εσA(T₁⁴-T₂⁴), di mana ε adalah emisivitas permukaan, σ adalah konstanta Stefan-Boltzmann, A adalah luas permukaan, dan T₁ dan T₂ adalah suhu absolut dari permukaan pemancar dan sekitarnya. Efisiensi radiasi dalam sistem pneumatik terutama bergantung pada emisivitas permukaan, perbedaan suhu, dan faktor pandangan antara komponen dan lingkungannya.
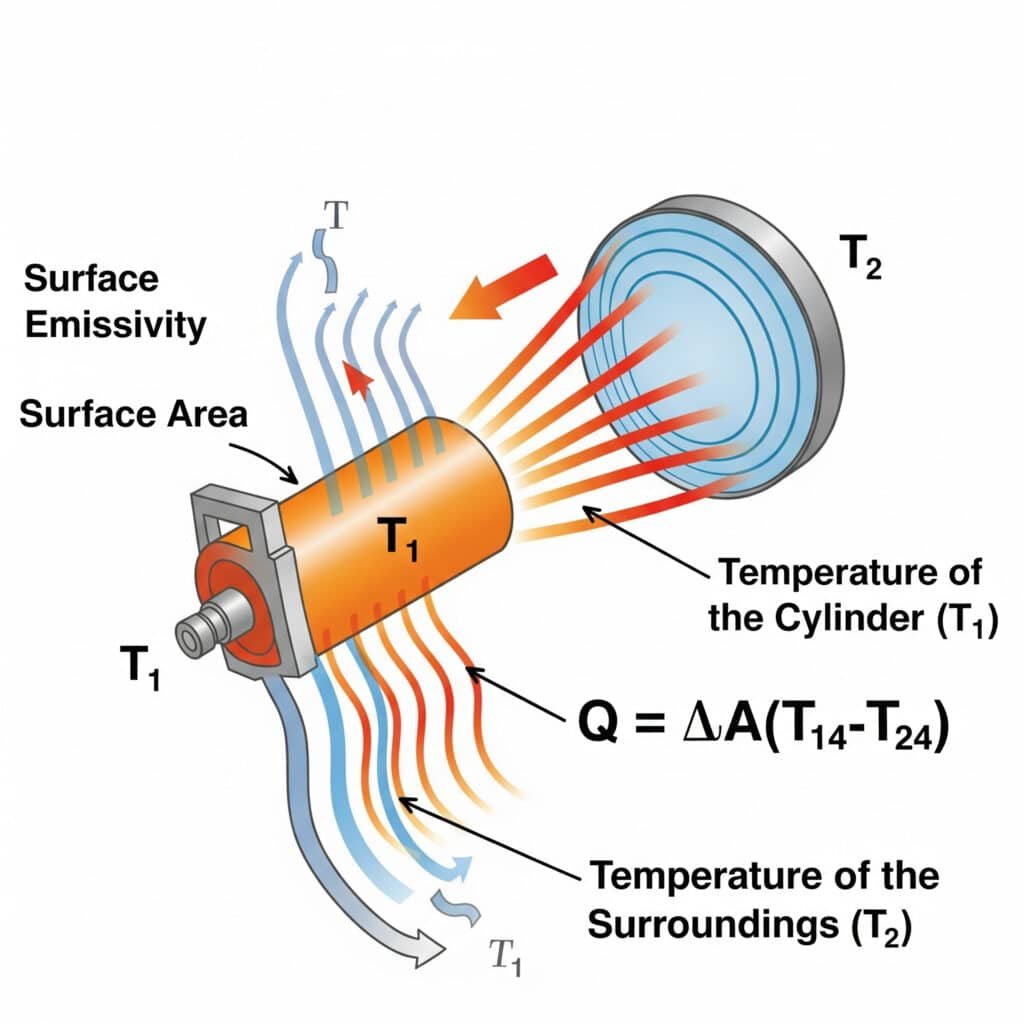
Baru-baru ini saya membantu produsen peralatan semikonduktor di Oregon mengatasi masalah panas berlebih dengan silinder tanpa batang presisi mereka. Para insinyur mereka hanya berfokus pada konduksi dan konveksi, tetapi mengabaikan radiasi. Dengan menerapkan lapisan emisivitas tinggi (meningkatkan ε dari 0,11 menjadi 0,92), kami meningkatkan perpindahan panas radiasi lebih dari 700%. Solusi pasif yang sederhana ini mengurangi suhu pengoperasian hingga 9°C tanpa bagian yang bergerak atau konsumsi energi-suatu persyaratan penting dalam lingkungan ruang bersih mereka.
Dasar-dasar Perpindahan Panas Radiasi
Persamaan dasar yang mengatur perpindahan panas radiatif adalah:
Q = εσA (T₁⁴-T₂⁴)
Dimana:
- Q = Laju perpindahan panas (W)
- ε = Emisivitas (tidak berdimensi, 0-1)
- σ = Konstanta Stefan-Boltzmann (5,67 × 10-⁸ W/m²-K⁴)
- A = Luas permukaan (m²)
- T₁ = Suhu absolut permukaan (K)
- T₂ = Suhu absolut di sekeliling (K)
Nilai Emisivitas Permukaan untuk Bahan Pneumatik Umum
| Bahan / Permukaan | Emisivitas (ε) | Efisiensi Radiasi | Potensi Peningkatan |
|---|---|---|---|
| Aluminium yang Dipoles | 0.04-0.06 | Sangat Buruk | > Peningkatan 1500% dimungkinkan |
| Aluminium Anodized | 0.7-0.9 | Luar biasa | Sudah dioptimalkan |
| Baja Tahan Karat (dipoles) | 0.07-0.14 | Miskin | Peningkatan >600% dimungkinkan |
| Baja Tahan Karat (teroksidasi) | 0.6-0.85 | Bagus. | Peningkatan sedang mungkin terjadi |
| Baja (dipoles) | 0.07-0.10 | Miskin | > Peningkatan 900% mungkin terjadi |
| Baja (teroksidasi) | 0.7-0.9 | Luar biasa | Sudah dioptimalkan |
| Permukaan yang Dicat | 0.8-0.98 | Luar biasa | Sudah dioptimalkan |
| PTFE (putih) | 0.8-0.9 | Luar biasa | Sudah dioptimalkan |
| Karet Nitril | 0.86-0.94 | Luar biasa | Sudah dioptimalkan |
Pertimbangan Faktor Tampilan
Pertukaran radiasi tidak hanya bergantung pada emisivitas tetapi juga pada hubungan geometris antar permukaan:
F₁₂ = Fraksi radiasi yang meninggalkan permukaan 1 yang mengenai permukaan 2
Untuk geometri yang rumit, faktor tampilan dapat dihitung dengan menggunakan:
- Solusi analitis untuk geometri sederhana
- Melihat aljabar faktor untuk menggabungkan solusi yang diketahui
- Metode numerik untuk pengaturan yang kompleks
- Perkiraan empiris untuk teknik praktis
Ketergantungan Suhu Radiasi
Hubungan suhu pangkat empat membuat radiasi khususnya efektif pada suhu yang lebih tinggi:
| Suhu Permukaan | Persentase Perpindahan Panas oleh Radiasi*. |
|---|---|
| 30°C (303K) | 5-15% |
| 50°C (323K) | 10-25% |
| 75°C (348K) | 15-35% |
| 100°C (373K) | 25-45% |
| 150°C (423K) | 35-60% |
*Dengan asumsi kondisi konveksi alami, ε = 0,8, suhu lingkungan 25°C
Strategi Peningkatan Efisiensi Radiasi
Berdasarkan pengalaman saya dengan sistem pneumatik industri, berikut ini adalah pendekatan yang paling efektif untuk meningkatkan perpindahan panas radiasi:
Modifikasi Emisivitas Permukaan
Pelapis dengan Emisivitas Tinggi
- Anodisasi hitam untuk aluminium (ε ≈ 0,8-0,9)
- Oksida hitam untuk baja (ε ≈ 0,7-0,8)
- Pelapis keramik khusus (ε ≈ 0,9-0,98)Tekstur Permukaan
- Pengasahan mikro meningkatkan emisivitas yang efektif
- Permukaan berpori meningkatkan sifat radiatif
- Peningkatan emisivitas/konveksi gabungan
Optimalisasi Lingkungan
Manajemen Suhu Lingkungan Sekitar
- Melindungi dari peralatan/proses yang panas
- Dinding/langit-langit yang sejuk untuk pertukaran radiasi yang lebih baik
- Hambatan reflektif untuk mengarahkan radiasi ke permukaan yang lebih dinginLihat Peningkatan Faktor
- Orientasi untuk memaksimalkan eksposur ke permukaan yang sejuk
- Penghapusan objek yang menghalangi
- Reflektor untuk meningkatkan pertukaran radiasi dengan area yang lebih dingin
Studi Kasus: Peningkatan Radiasi dalam Pneumatik Presisi
Untuk silinder tanpa batang presisi tinggi di lingkungan ruang bersih:
| Parameter | Desain Asli | Desain yang Ditingkatkan Radiasi | Peningkatan |
|---|---|---|---|
| Bahan Permukaan | Aluminium yang Dipoles (ε ≈ 0,06) | Aluminium Berlapis Keramik (ε ≈ 0,94) | Peningkatan emisivitas 1467% |
| Perpindahan Panas Radiasi | 2.1W | 32.7W | Peningkatan radiasi 1457% |
| Suhu Operasi | 68°C | 59°C | Pengurangan 9°C |
| Umur Komponen | 8 bulan | > 24 bulan | 3 × peningkatan |
| Biaya Implementasi | – | $175 per silinder | Pengembalian modal 4,2 bulan |
Radiasi vs Mode Perpindahan Panas Lainnya
Memahami kapan radiasi mendominasi sangat penting untuk manajemen termal yang efisien:
| Kondisi | Dominasi Konduksi | Dominasi Konveksi | Dominasi Radiasi |
|---|---|---|---|
| Kisaran Suhu | Rendah ke Tinggi | Rendah hingga Sedang | Sedang hingga Tinggi |
| Properti Material | Bahan k tinggi | K rendah, luas permukaan tinggi | Permukaan ε yang tinggi |
| Faktor Lingkungan | Kontak termal yang baik | Udara yang bergerak, kipas angin | Perbedaan suhu yang besar |
| Batasan Ruang | Kemasan yang ketat | Aliran udara terbuka | Pemandangan ke lingkungan yang lebih sejuk |
| Aplikasi Terbaik | Antarmuka komponen | Pendinginan umum | Permukaan panas, vakum, udara diam |
Kesimpulan
Menguasai prinsip-prinsip perpindahan panas-penghitungan koefisien konduksi, metode peningkatan konveksi, dan pemodelan efisiensi radiasi-memberikan fondasi untuk manajemen termal yang efektif dalam sistem pneumatik. Dengan menerapkan prinsip-prinsip ini, Anda dapat mengurangi suhu pengoperasian, memperpanjang masa pakai komponen, dan meningkatkan efisiensi energi sekaligus memastikan pengoperasian yang andal bahkan di lingkungan yang menantang.
Tanya Jawab Tentang Perpindahan Panas dalam Sistem Pneumatik
Berapa kenaikan suhu yang biasa terjadi pada silinder pneumatik selama pengoperasian?
Silinder pneumatik biasanya mengalami kenaikan suhu 20-40 ° C di atas suhu sekitar selama pengoperasian terus-menerus. Kenaikan ini diakibatkan oleh gesekan antara seal dan dinding silinder, pemanasan kompresi udara, dan kerja mekanis yang diubah menjadi panas. Silinder tanpa batang sering mengalami kenaikan suhu yang lebih tinggi (30-50 ° C) karena sistem penyegelan yang lebih kompleks dan pembentukan panas yang terkonsentrasi di rakitan bantalan / segel.
Bagaimana tekanan operasi memengaruhi pembangkitan panas dalam sistem pneumatik?
Tekanan operasi memiliki dampak yang signifikan terhadap pembangkitan panas, dengan tekanan yang lebih tinggi menghasilkan lebih banyak panas melalui beberapa mekanisme. Setiap peningkatan 1 bar pada tekanan operasi biasanya meningkatkan pembangkitan panas sebesar 8-12% karena gaya gesekan yang lebih besar antara seal dan permukaan, pemanasan kompresi yang lebih tinggi, dan peningkatan kerugian terkait kebocoran. Hubungan ini kira-kira linier dalam rentang operasi normal (3-10 bar).
Apa pendekatan pendinginan yang optimal untuk komponen pneumatik di lingkungan yang berbeda?
Pendekatan pendinginan yang optimal bervariasi menurut lingkungan: pada pengaturan suhu sedang yang bersih (15-30°C), konveksi alami dengan jarak antar komponen yang tepat sering kali sudah cukup. Pada lingkungan bersuhu tinggi (30-50°C), konveksi paksa dengan menggunakan kipas atau udara bertekanan menjadi perlu. Dalam kondisi yang sangat panas (>50°C) atau di mana aliran udara dibatasi, metode pendinginan aktif seperti pendingin termoelektrik atau pendingin cair mungkin diperlukan. Dalam semua kasus, memaksimalkan radiasi melalui permukaan emisivitas tinggi memberikan pendinginan pasif tambahan.
Bagaimana cara menghitung total perpindahan panas dari komponen pneumatik?
Hitung perpindahan panas total dengan menjumlahkan kontribusi dari setiap mekanisme: Qtotal = Qkonduksi + Qkonveksi + Qradiasi. Untuk konduksi, gunakan Q = kA (T₁-T₂) / L untuk setiap jalur panas. Untuk konveksi, gunakan Q = hA (Ts-T∞) dengan koefisien konveksi yang sesuai. Untuk radiasi, gunakan Q = εσA (T₁⁴-T₂⁴). Pada sebagian besar aplikasi pneumatik industri yang beroperasi pada suhu 30-80°C, perkiraan distribusi adalah konduksi 20-40%, konveksi 40-70%, dan radiasi 10-30%.
Apa hubungan antara suhu dan masa pakai komponen pneumatik?
Umur komponen berkurang secara eksponensial dengan meningkatnya suhu, mengikuti hubungan Arrhenius yang dimodifikasi. Sebagai aturan praktis, setiap kenaikan 10°C pada suhu pengoperasian mengurangi masa pakai seal dan komponen sebesar 40-50%. Ini berarti komponen yang beroperasi pada suhu 70 ° C mungkin hanya bertahan sepertiga lebih lama dari komponen yang sama pada suhu 50 ° C. Hubungan ini sangat penting untuk komponen polimer seperti seal, bearing, dan gasket, yang sering kali menentukan interval perawatan untuk sistem pneumatik.
-
Memberikan penjelasan dasar tentang Hukum Fourier, prinsip dasar yang menjelaskan bagaimana panas dihantarkan melalui material padat berdasarkan konduktivitas termal dan gradien suhunya. ↩
-
Menjelaskan fungsi dan jenis Thermal Interface Material (TIM), yang digunakan untuk mengisi celah udara mikroskopis di antara komponen untuk meningkatkan konduksi panas dan mengurangi hambatan termal. ↩
-
Merinci prinsip-prinsip Hukum Pendinginan Newton, yang mengatur bagaimana benda mendingin dengan mentransfer panas ke fluida di sekitarnya melalui konveksi, sebuah faktor kunci dalam desain sistem pendingin. ↩
-
Menawarkan pandangan mendalam tentang bilangan Nusselt, sebuah kuantitas penting tanpa dimensi dalam dinamika fluida dan perpindahan panas yang merepresentasikan rasio perpindahan panas konvektif dan konduktif melintasi batas. ↩
-
Menjelaskan Hukum Stefan-Boltzmann, prinsip fisika dasar yang mengukur total energi yang dipancarkan oleh benda hitam, yang sangat penting untuk menghitung kehilangan panas dari permukaan yang panas. ↩



