Bagaimana Resonansi Getaran Berdampak pada Kinerja Peralatan Industri?

Mimpi buruk setiap teknisi pemeliharaan adalah kegagalan peralatan yang tidak terduga. Ketika mesin bergetar pada frekuensi alami mereka, kerusakan besar dapat terjadi dalam hitungan menit. Saya telah melihat masalah ini merugikan perusahaan hingga ribuan kali lipat dalam hal waktu henti.

Resonansi getaran¹ terjadi ketika gaya eksternal sesuai dengan frekuensi alami sistem, menyebabkan osilasi yang diperkuat yang dapat merusak peralatan. Memahami dan mengendalikan fenomena ini sangat penting untuk mencegah kegagalan dan memperpanjang masa pakai alat berat.

Izinkan saya berbagi cerita singkat. Tahun lalu, seorang pelanggan dari Jerman menelepon saya dengan panik. Lini produksi mereka telah berhenti karena sebuah silinder tanpa batang bergetar hebat. Masalahnya? Resonansi. Pada akhir artikel ini, Anda akan memahami cara mengidentifikasi dan mencegah masalah serupa di sistem Anda.

Daftar Isi

Rumus Frekuensi Alami: Bagaimana Anda Dapat Menghitung Titik-Titik Rentan Sistem Anda?
Model Pegas Massa: Mengapa Pendekatan Sederhana Ini Sangat Berharga?
Optimalisasi Rasio Redaman: Eksperimen Apa yang Memberikan Hasil Terbaik?
Kesimpulan
Tanya Jawab Tentang Resonansi Getaran

Rumus Frekuensi Alami: Bagaimana Anda Dapat Menghitung Titik-Titik Rentan Sistem Anda?

Memahami frekuensi alami peralatan Anda adalah langkah pertama untuk mencegah masalah resonansi. Nilai kritis ini menentukan kapan sistem Anda paling rentan terhadap masalah getaran.

The frekuensi alami² (fn) suatu sistem dapat dihitung dengan menggunakan rumus: fn = (1/2π) × √(k/m), di mana k adalah koefisien kekakuan dan m adalah massa. Perhitungan ini menunjukkan frekuensi di mana sistem Anda akan beresonansi jika tereksitasi oleh gaya eksternal yang sesuai.

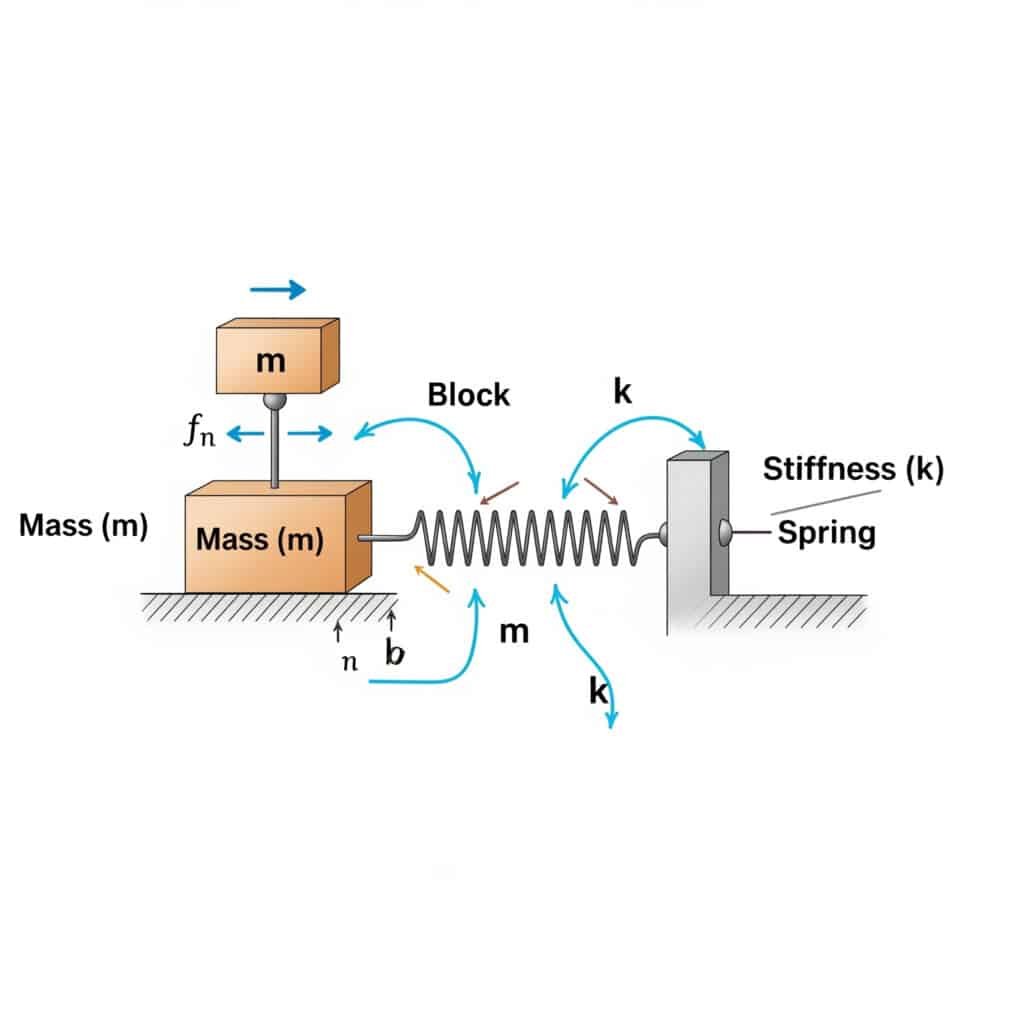
Diagram yang jelas dan mendidik yang menjelaskan frekuensi alami. Ilustrasi ini menampilkan sistem massa-pegas sederhana, dengan blok berlabel 'Massa (m)' dan pegas berlabel 'Kekakuan (k)'. Garis gerak menunjukkan sistem berosilasi. Berdekatan dengan diagram, rumus 'fn = (1/2π) × √(k/m)' ditampilkan dengan jelas, dengan panah yang secara eksplisit menghubungkan variabel 'm' dan 'k' dalam persamaan ke bagian fisik yang sesuai. — frekuensi alami

Ketika saya mengunjungi sebuah pabrik manufaktur di Swiss, saya melihat silinder pneumatik tanpa batang mereka mengalami kerusakan sebelum waktunya. Tim pemeliharaan mereka tidak menghitung frekuensi alami dari pengaturan mereka. Setelah menerapkan rumus ini, kami mengidentifikasi bahwa kecepatan operasi mereka sangat dekat dengan frekuensi alami sistem.

Aplikasi Praktis Perhitungan Frekuensi Alami

Rumus frekuensi natural tidak hanya bersifat teoretis-ini memiliki aplikasi langsung dalam berbagai pengaturan industri:

Pemilihan Peralatan: Memilih komponen dengan frekuensi alami yang jauh dari kondisi pengoperasian Anda
Perawatan Pencegahan: Menjadwalkan inspeksi berdasarkan profil risiko getaran
Pemecahan masalah: Mengidentifikasi akar penyebab getaran yang tidak terduga

Nilai Frekuensi Alami Umum untuk Komponen Industri

Komponen	Kisaran Frekuensi Alami Umum (Hz)
Silinder Tanpa Batang	10-50 Hz
Braket Pemasangan	20-100 Hz
Struktur Pendukung	5-30 Hz
Katup Kontrol	40-200 Hz

Faktor-faktor Penting yang Mempengaruhi Frekuensi Alami

Perhitungan frekuensi natural tampak sederhana, tetapi beberapa faktor dapat mempersulit aplikasi di dunia nyata:

Distribusi massa yang tidak seragam: Sebagian besar komponen industri tidak memiliki massa yang terdistribusi secara sempurna
Kekakuan variabel: Komponen mungkin memiliki kekakuan yang berbeda pada arah yang berbeda
Titik koneksi: Cara pemasangan komponen secara signifikan memengaruhi karakteristik getarannya
Efek suhu: Sifat massa dan kekakuan dapat berubah dengan suhu

Model Pegas Massa: Mengapa Pendekatan Sederhana Ini Sangat Berharga?

Model pegas-massa memberikan kerangka kerja intuitif untuk memahami sistem getaran yang kompleks. Model ini mereduksi mesin yang rumit menjadi elemen-elemen dasar yang dapat dengan mudah dianalisis oleh para insinyur.

The model pegas massa³ menyederhanakan analisis getaran dengan merepresentasikan sistem mekanis sebagai massa diskrit yang dihubungkan oleh pegas. Pendekatan ini memungkinkan para insinyur untuk memprediksi perilaku sistem, mengidentifikasi potensi masalah resonansi, dan mengembangkan solusi yang efektif tanpa matematika yang rumit.

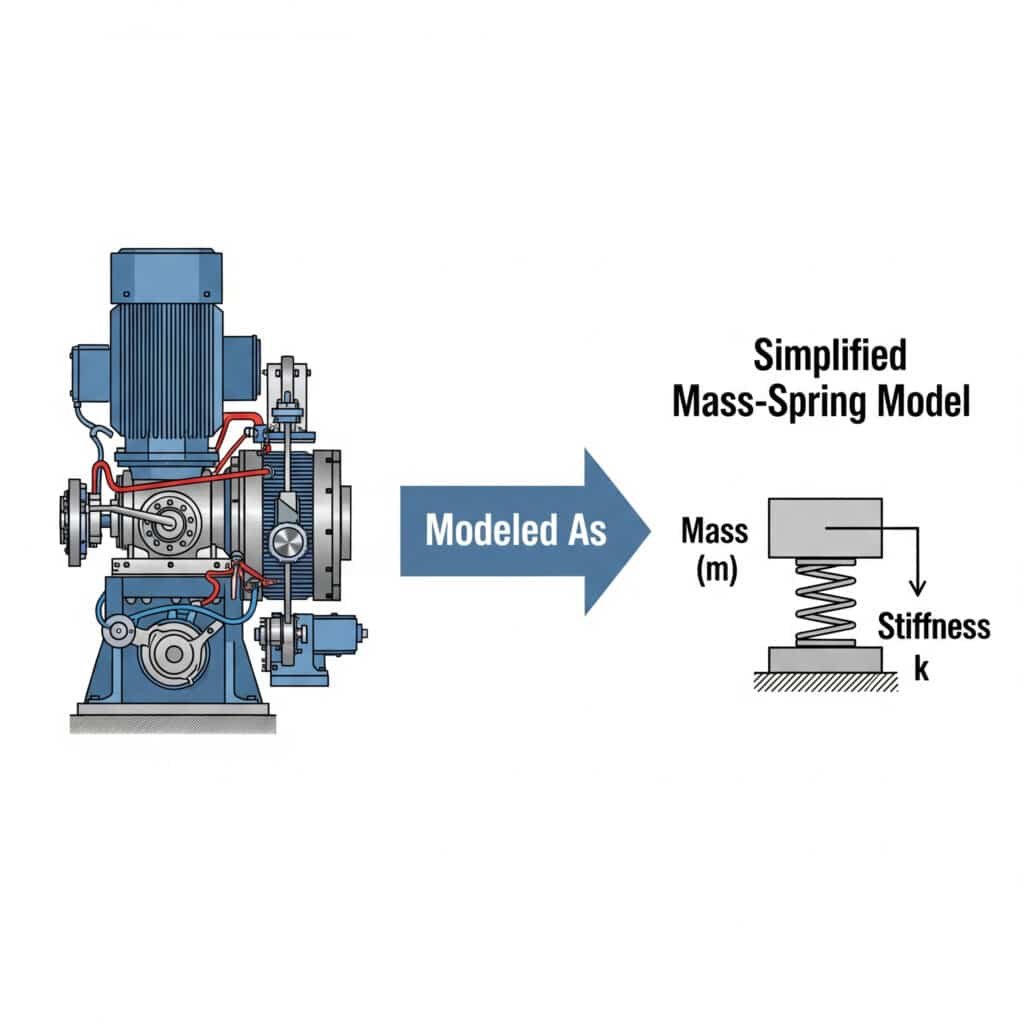
Infografis komparatif yang menjelaskan model pegas-massa. Di sebelah kiri, di bawah label 'Sistem Mekanik Kompleks', adalah ilustrasi terperinci dari motor industri. Panah besar berlabel 'Modeled As' menunjuk ke kanan. Di sebelah kanan, di bawah label 'Model Pegas-Massa yang Disederhanakan,' seluruh motor yang kompleks diwakili oleh blok sederhana berlabel 'Massa (m)' yang terhubung ke pegas sederhana berlabel 'Kekakuan (k)'. — model pegas massa

Saya ingat pernah bekerja dengan produsen suku cadang otomotif di Michigan yang tidak dapat memahami mengapa silinder tanpa batang yang dipandu mereka mengalami kegagalan. Dengan memodelkan sistem mereka sebagai pengaturan pegas massa sederhana, kami mengidentifikasi bahwa braket pemasangan bertindak sebagai pegas yang tidak diinginkan, menciptakan kondisi resonansi.

Mengonversi Sistem Nyata ke Model Pegas-Massa

Untuk menerapkan pendekatan ini pada peralatan Anda:

Mengidentifikasi massa utama: Menentukan komponen mana yang memberikan kontribusi bobot yang signifikan
Temukan elemen pegas: Menemukan komponen yang menyimpan dan melepaskan energi (pegas aktual, dudukan fleksibel, dll.)
Koneksi peta: Mendokumentasikan bagaimana massa dan pegas berinteraksi
Menyederhanakan: Menggabungkan elemen yang serupa untuk membuat model yang dapat dikelola

Jenis-jenis Sistem Pegas Massa

Jenis Sistem	Deskripsi	Aplikasi Umum
DOF tunggal	Satu massa dengan satu pegas	Silinder pneumatik sederhana
Multi-DOF	Beberapa massa dengan beberapa pegas	Mesin yang kompleks dengan banyak komponen
Berkelanjutan	DOF tak terbatas (memerlukan analisis yang berbeda)	Balok, pelat, dan cangkang

Pertimbangan Pemodelan Tingkat Lanjut

Meskipun model pegas-massa dasar sangat berharga, namun ada beberapa penyempurnaan yang membuatnya lebih realistis:

Menambahkan peredam: Sistem nyata selalu memiliki disipasi energi
Mempertimbangkan nonlinieritas: Mata air tidak selalu mengikuti Hukum Hooke⁴ sempurna
Memperhitungkan getaran paksa: Kekuatan eksternal mengubah perilaku sistem
Termasuk efek penggabungan: Pergerakan ke satu arah dapat memengaruhi arah lainnya

Optimalisasi Rasio Redaman: Eksperimen Apa yang Memberikan Hasil Terbaik?

Peredaman adalah pertahanan terbaik Anda terhadap masalah resonansi. Menemukan rasio redaman yang optimal melalui eksperimen dapat secara dramatis meningkatkan kinerja dan keandalan sistem.

Rasio redaman⁵ Eksperimen pengoptimalan melibatkan pengujian secara sistematis terhadap konfigurasi peredaman yang berbeda untuk menemukan keseimbangan ideal antara kontrol getaran dan daya tanggap sistem. Rasio redaman optimal biasanya berada di antara 0,2 dan 0,7, yang memberikan peredaman getaran yang cukup tanpa kehilangan energi yang berlebihan.

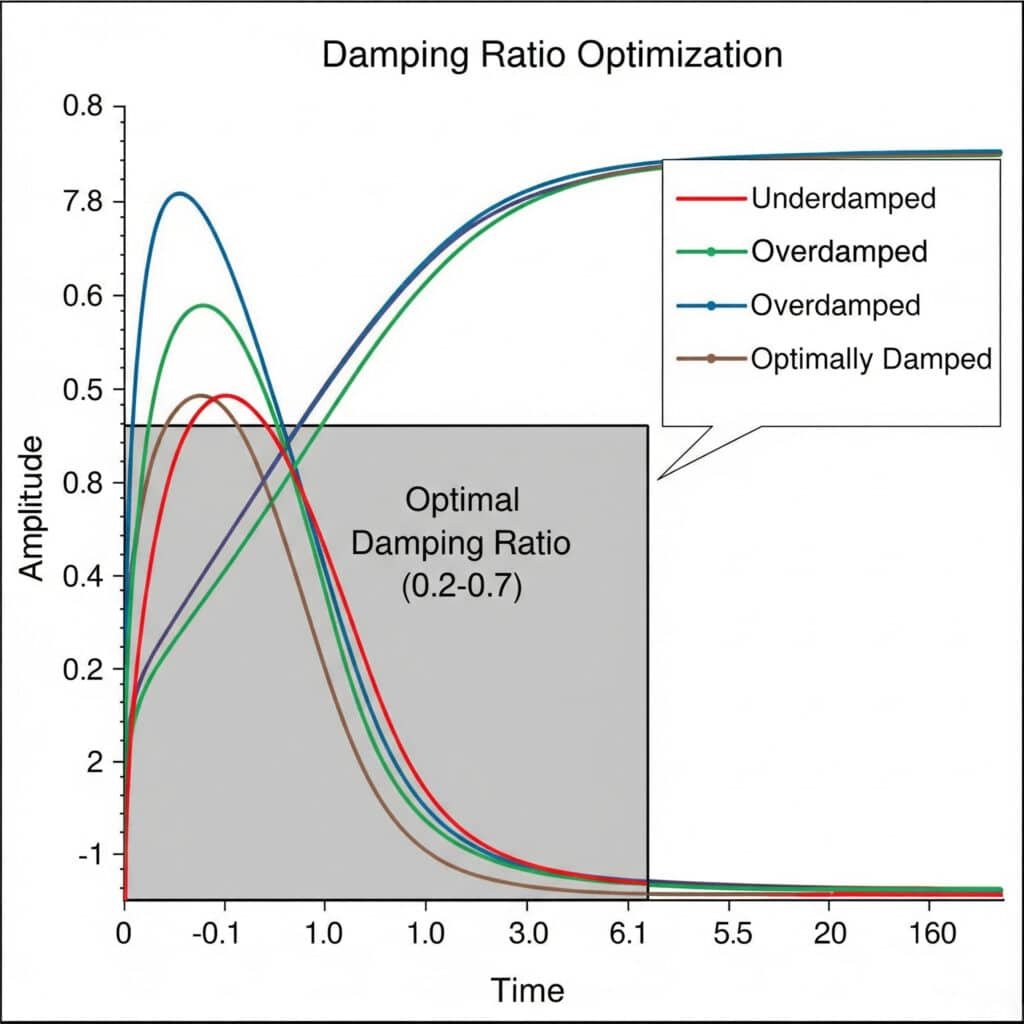
Grafik yang mengilustrasikan optimasi rasio redaman dengan memplotkan 'Amplitudo' sistem versus 'Waktu'. Grafik ini menampilkan tiga kurva respons yang berbeda: kurva 'Underdamped' yang berosilasi secara signifikan, kurva 'Overdamped' yang kembali ke nol dengan sangat lambat tanpa osilasi, dan kurva 'Optimally Damped' yang stabil secara cepat dengan overshoot minimal. Wilayah yang diarsir menyoroti respons ideal ini, yang diberi label 'Rasio Peredaman Optimal (0,2-0,7)'. — pengoptimalan rasio redaman

Bulan lalu, saya membantu produsen peralatan pengolahan makanan di Prancis memecahkan masalah getaran yang terus-menerus dalam silinder tanpa batang magnetik mereka. Melalui serangkaian eksperimen rasio redaman, kami menemukan bahwa desain asli mereka hanya memiliki rasio redaman 0,05 - terlalu rendah untuk mencegah masalah resonansi.

Pengaturan Eksperimental untuk Pengujian Rasio Redaman

Untuk melakukan eksperimen pengoptimalan redaman yang efektif:

Pengukuran dasar: Rekam respons sistem tanpa redaman tambahan
Pengujian tambahan: Menambahkan elemen redaman dalam kenaikan terkendali
Pengukuran respons: Mengukur amplitudo, waktu pengendapan, dan respons frekuensi
Analisis data: Menghitung rasio redaman untuk setiap konfigurasi
Validasi: Memverifikasi kinerja dalam kondisi pengoperasian aktual

Perbandingan Teknologi Peredaman

Teknologi Peredaman	Keuntungan	Keterbatasan	Aplikasi Khas
Peredam Kental	Performa yang dapat diprediksi, suhu stabil	Membutuhkan perawatan, potensi kebocoran	Mesin berat, peralatan presisi
Peredam Gesekan	Desain sederhana, hemat biaya	Keausan dari waktu ke waktu, perilaku nonlinier	Dukungan struktural, mesin dasar
Peredaman Material	Tidak ada bagian yang bergerak, ringkas	Rentang penyesuaian terbatas	Instrumen presisi, isolasi getaran
Peredaman Aktif	Dapat beradaptasi dengan kondisi yang berubah-ubah	Rumit, membutuhkan daya	Aplikasi kritis, peralatan berkecepatan variabel

Mengoptimalkan Peredaman untuk Berbagai Kondisi Pengoperasian

Rasio peredaman yang ideal tidak bersifat universal-tergantung pada aplikasi spesifik Anda:

Operasi kecepatan tinggi: Rasio redaman yang lebih rendah (0,1-0,3) mempertahankan responsifitas
Aplikasi presisi: Rasio redaman yang lebih tinggi (0,5-0,7) memberikan stabilitas
Sistem beban variabel: Peredaman adaptif mungkin diperlukan
Lingkungan yang sensitif terhadap suhu: Pertimbangkan bahan peredam dengan sifat stabil

Studi Kasus: Optimalisasi Peredaman Silinder Tanpa Batang

Saat mengoptimalkan silinder tanpa batang kerja ganda untuk mesin pengemasan, kami menguji lima konfigurasi redaman yang berbeda:

Bantal ujung standar: Rasio redaman = 0,12
Bantal yang diperpanjang: Rasio redaman = 0,25
Peredam kejut eksternal: Rasio redaman = 0,41
Braket pemasangan komposit: Rasio redaman = 0,38
Pendekatan gabungan (3+4): Rasio redaman = 0,53

Pendekatan gabungan memberikan performa terbaik, mengurangi amplitudo getaran sebesar 78% sekaligus mempertahankan waktu respons yang dapat diterima.

Kesimpulan

Memahami resonansi getaran melalui perhitungan frekuensi alami, pemodelan pegas-massa, dan pengoptimalan rasio redaman sangat penting untuk mencegah kegagalan peralatan. Dengan menerapkan prinsip-prinsip ini, Anda dapat memperpanjang usia alat berat, mengurangi waktu henti, dan meningkatkan kinerja sistem secara keseluruhan.

Tanya Jawab Tentang Resonansi Getaran

Apa yang dimaksud dengan resonansi getaran dalam peralatan industri?

Resonansi getaran terjadi ketika gaya eksternal cocok dengan frekuensi alami sistem, menyebabkan osilasi yang diperkuat. Pada peralatan industri, fenomena ini dapat menyebabkan gerakan yang berlebihan, kelelahan komponen, dan kegagalan yang sangat besar jika tidak dikelola dengan baik.

Bagaimana cara mengidentifikasi jika sistem saya mengalami resonansi?

Carilah gejala seperti peningkatan kebisingan yang tidak dapat dijelaskan, getaran yang terlihat pada kecepatan tertentu, kerusakan komponen yang terlalu dini, dan penurunan performa yang terjadi pada titik operasi yang konsisten. Alat analisis getaran dapat mengonfirmasi kondisi resonansi.

Apa perbedaan antara getaran paksa dan resonansi?

Getaran paksa terjadi setiap kali ada gaya eksternal yang bekerja pada suatu sistem, sedangkan resonansi adalah kondisi spesifik ketika frekuensi paksa tersebut sesuai dengan frekuensi alami sistem, sehingga menghasilkan respons yang diperkuat. Semua resonansi melibatkan getaran paksa, tetapi tidak semua getaran paksa menyebabkan resonansi.

Bagaimana desain silinder pneumatik tanpa batang memengaruhi karakteristik getarannya?

Desain silinder pneumatik tanpa batang-dengan gerbong yang bergerak, sistem penyegelan internal, dan mekanisme pemandu-menciptakan tantangan getaran yang unik. Profil yang diperpanjang bertindak sebagai balok yang dapat melentur, massa kereta menciptakan gaya inersia, dan pita penyegelan dapat menimbulkan gesekan yang bervariasi.

Modifikasi sederhana apa yang dapat mengurangi resonansi pada peralatan yang sudah ada?

Untuk peralatan yang sudah ada yang mengalami masalah resonansi, pertimbangkan untuk menambahkan massa untuk mengubah frekuensi alami, memasang peredam eksternal atau peredam kejut, memodifikasi metode pemasangan untuk menyertakan isolasi getaran, atau menyesuaikan kecepatan operasi untuk menghindari frekuensi resonansi.

Memberikan penjelasan dasar tentang resonansi mekanis, sering kali dengan contoh visual, yang menunjukkan bagaimana gaya periodik kecil dapat menghasilkan osilasi amplitudo besar dalam suatu sistem. ↩
Menawarkan pandangan terperinci tentang fisika frekuensi alami, frekuensi spesifik di mana sistem cenderung berosilasi tanpa adanya gaya pendorong atau peredam. ↩
Menjelaskan prinsip-prinsip model massa-pegas, sebuah idealisasi fundamental dalam fisika dan teknik yang digunakan untuk menganalisis sistem kompleks yang menunjukkan gerak harmonik sederhana. ↩
Detail Hukum Hooke, sebuah prinsip fisika yang menyatakan bahwa gaya yang dibutuhkan untuk memanjangkan atau memampatkan pegas sejauh tertentu berbanding lurus dengan jarak tersebut. ↩
Menjelaskan rasio redaman, ukuran tanpa dimensi yang mendefinisikan bagaimana osilasi dalam sistem meluruh setelah terjadi gangguan, yang sangat penting untuk mengendalikan resonansi. ↩

Terkait

Cara Memilih Silinder Tahan Korosi untuk Aplikasi Kelautan

Panduan Langkah-demi-Langkah: Mengganti Silinder ISO 6432 Pesaing

Mengintegrasikan Silinder Ringkas ke dalam Jalur Perakitan PCB Otomatis

Halo, saya Chuck, seorang ahli senior dengan pengalaman 15 tahun di industri pneumatik. Di Bepto Pneumatic, saya fokus untuk memberikan solusi pneumatik berkualitas tinggi yang dibuat khusus untuk klien kami. Keahlian saya meliputi otomasi industri, desain dan integrasi sistem pneumatik, serta aplikasi dan pengoptimalan komponen utama. Jika Anda memiliki pertanyaan atau ingin mendiskusikan kebutuhan proyek Anda, jangan ragu untuk menghubungi saya di chuck@bepto.com.