
ガスの誤解は、年間何十億もの産業損失を引き起こしている。エンジニアはしばしば気体を液体や固体のように扱い、致命的なシステムの故障や安全上の危険を引き起こします。基本的なガスの概念を理解することで、コストのかかるミスを防ぎ、システムのパフォーマンスを最適化することができます。
気体とは、分子が常にランダムに運動していることを特徴とする物質の状態である。 分子間力1圧力、体積、温度の関係によって支配される圧縮性の挙動を示しながら、あらゆる容器を完全に満たす。
昨年、私はクラウス・ミューラーというドイツの化学エンジニアのコンサルティングを行った。彼のチームは、液体ベースの計算を気体システムに適用していました。基本的な気体の概念を説明し、適切な気体挙動モデルを導入した結果、圧力変動がなくなり、プロセス効率が42%向上した。
目次
- 物質の状態としての気体を定義するものは何か?
- 気体分子はミクロのレベルでどのように振る舞うのか?
- 気体の基本的性質とは?
- 気体の圧力、体積、温度はどのように影響し合うのか?
- 産業用途におけるガスの種類とは?
- 工業用ガスの挙動を支配する気体の法則とは?
- 結論
- ガスの基本概念に関するFAQ
物質の状態としての気体を定義するものは何か?
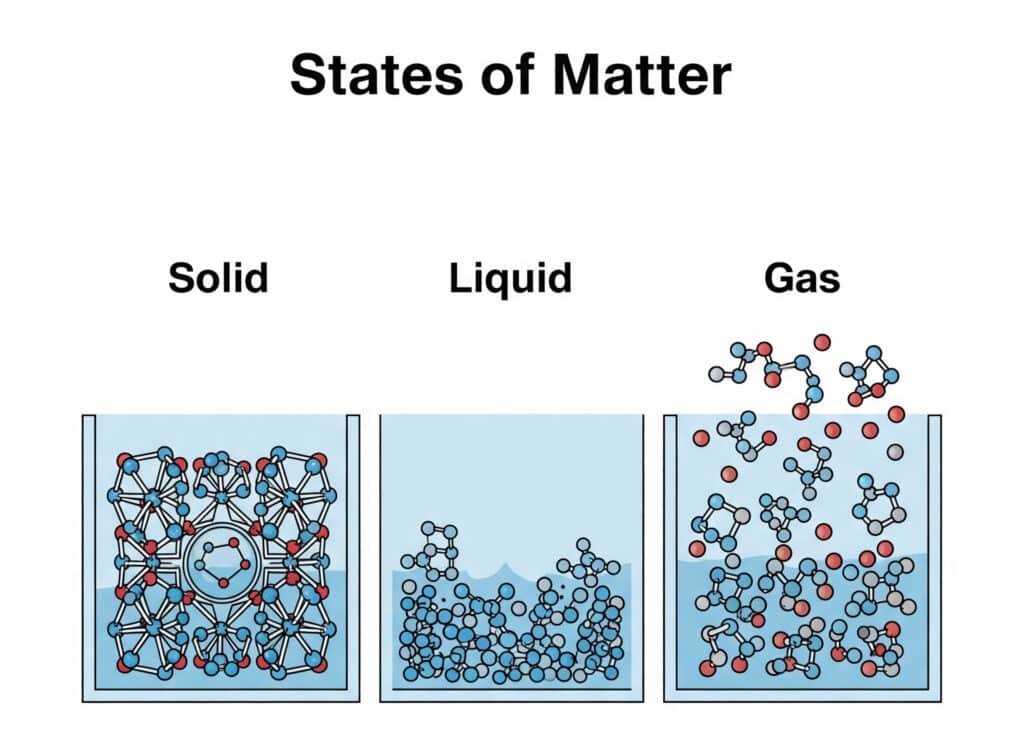
気体は物質の基本的な状態のひとつであり、固体や液体とは異なる独特の分子配列と挙動によって区別される。
気体は、最小限の分子間引力によって連続的にランダムに運動する分子によって定義され、液体や固体に比べて圧縮可能な特性と低密度を維持しながら、あらゆる容器を満たすための完全な膨張を可能にする。
分子配列の特徴
気体分子は非常に無秩序な状態で存在し、動きの自由度が最大であるため、独特の物理的・化学的性質が生まれる。
主な分子の特徴
| 特徴 | ガス州 | 液状 | ソリッドステート |
|---|---|---|---|
| 分子間隔 | 非常に大きい(直径10倍) | 小(直径1倍) | 固定ポジション |
| 分子運動 | ランダム、高速 | ランダム、制限付き | 振動のみ |
| 分子間力 | ごくわずか | 中程度 | 強い |
| 形状 | 形が決まっていない | 形が決まっていない | 固定形状 |
| ボリューム | 容器への充填 | 固定ボリューム | 固定ボリューム |
圧縮特性
固体や液体とは異なり、気体は分子間に大きな空間があるため大きな圧縮性を示し、圧力がかかるとその空間が小さくなる。
圧縮性の比較:
- ガス:圧縮性が高い(圧力によって体積が大きく変化する)
- 液体:わずかに圧縮性(体積変化が少ない)
- 固体:ほぼ非圧縮性(体積変化はごくわずか)
- 理想気体の場合、Z≒1
- 高圧の実ガスの場合、Z < 1
- 超高圧の実ガスの場合、Z > 1
密度特性
気体の密度は、分子間の間隔が大きいため、液体や固体に比べて著しく低く、圧力や温度によって劇的に変化する。
密度の関係:
- ガス密度:0.001~0.01g/cm³(標準状態において)
- 液体密度:0.5~2.0g/cm³(標準範囲)
- 固体密度:1~20g/cm³(標準範囲)
気体密度の公式ρ = PM/(RT)
どこでだ:
- P = 圧力
- M = 分子量
- R = 万有引力気体定数
- T = 絶対温度
伸縮挙動
気体は、予測可能な熱力学的関係に従って、温度と圧力の変化に伴って劇的な膨張と収縮を示す。
拡張特性:
- 熱膨張:温度による体積の著しい増加
- 圧力応答:体積は圧力に反比例する
- 無制限の拡張:空いているスペースはすべて埋める
- 迅速な平衡化:均一な状態に素早く到達
気体分子はミクロのレベルでどのように振る舞うのか?
気体の分子挙動は、微視的な分子運動と相互作用を通して巨視的な気体の特性を説明する運動論的な原理に従っている。
気体分子はマックスウェル・ボルツマン分布に従う速度でランダムな並進運動を示し、絶対温度に比例する平均運動エネルギーを維持しながら弾性衝突を経験する。
運動論3 基礎
運動論的分子理論は、分子運動の原理を通して気体の挙動を理解するための基礎を提供する。
基本的な運動理論の前提:
- 点粒子:気体分子の体積はごくわずか
- ランダム・モーション:分子は衝突するまで一直線に動く
- 弾性衝突:分子衝突時のエネルギー損失なし
- 分子間力なし:短時間の衝突を除く
- 温度の関係:平均運動エネルギー ∝ 絶対温度
分子速度分布
気体分子は、マックスウェル・ボルツマン分布に従うさまざまな速度を示し、ほとんどの分子は平均速度に近い。
速度分布パラメータ:
- 最も可能性の高い速度: vₘ = √(2RT_M/M)
- 平均速度: v̄ = √(8RT/πM)
- 二乗平均平方根速度: vᵣ = √(3RT_2098↩↪Lm_209B)
どこでだ:
- R = 万有引力気体定数
- T = 絶対温度
- M = 分子量
速度に対する温度の影響:
| 温度 | 平均速度(m/s) | 分子活性 |
|---|---|---|
| 273 K (0°C) | 461(空気分子) | 適度な動き |
| 373 K (100°C) | 540(空気分子) | 運動量の増加 |
| 573 K (300°C) | 668(空気分子) | 高エネルギー運動 |
衝突周波数と平均自由行程
気体分子は常に互いや容器の壁と衝突し、圧力や輸送特性を決定する。
衝突の特徴:
平均自由行程λ = 1/(√2 × n × σ)
どこでだ:
- n = 分子の数密度
- σ = 衝突断面積
衝突頻度ν = v̄/λ
標準状態での代表値:
- 平均自由行程68 nm (STPにおける空気)
- 衝突頻度7×10⁹衝突/秒
- 壁面衝突率2.7 × 10²³ 衝突/cm²・s
分子間のエネルギー分布
気体分子は温度によって運動エネルギーが変化し、温度が高いほどエネルギー分布が広くなる。
エネルギー・コンポーネント:
- 翻訳エネルギー: ½mv² (空間を通る運動)
- 回転エネルギー: ½Iω² (分子回転)
- 振動エネルギー:ポテンシャル+キネティック(分子振動)
平均並進エネルギー:Eₜᵣₛ = (3/2)kT
ここでk = ボルツマン定数
気体の基本的性質とは?
気体は、他の物質状態とは異なる独特の性質を示し、産業用途におけるその挙動を決定する。
基本的な気体の性質には、圧力、体積、温度、密度、圧縮性、粘性、熱伝導率などがあり、これらはすべて熱力学的な関係と分子の挙動によって相互に関連している。
圧力特性
気体の圧力は、分子と容器の壁との衝突によって生じ、単位面積当たりの力は分子密度と速度によって変化する。
圧力特性:
- 起源:分子と表面の衝突
- 単位:パスカル(Pa)、大気圧(atm)、PSI
- 測定:絶対圧とゲージ圧の比較
- バリエーション:温度と体積による変化
圧力関係:
運動論圧力:P = (1/3)nmv̄²である。
どこでだ:
- n = 数密度
- m = 分子質量
- v̄² = 平均二乗速度
ボリューム特性
気体の体積は、分子体積と分子間空間の両方を含む、分子が占める空間を表す。
ボリュームの特徴:
- コンテナ依存:ガスが空きスペースを完全に満たす
- 圧縮可能:体積は圧力によって大きく変化する
- 温度に敏感:温度が上がると膨張する
- モル体積:標準状態での1モルあたりの体積
標準的な条件:
- STP (標準温度と標準圧力):0℃、1気圧
- STPでのモル体積理想気体の場合:22.4 L/mol
- SATP (標準周囲温度):25℃、1バール
温度特性
温度は平均分子運動エネルギーを測定し、熱力学的関係を通じて気体の挙動を決定する。
温度効果:
| プロパティ | 温度上昇効果 | 人間関係 |
|---|---|---|
| 分子速度 | 増加 | v ∝ √T |
| 圧力(V一定) | 増加 | P ∝ T |
| 体積(P一定) | 増加 | V ∝ T |
| 密度(一定P) | 減少 | ρ ∝ 1/T |
密度と比容積
気体密度は圧力や温度によって大きく変化するため、工業計算において重要な特性となっている。
密度の関係:
理想気体密度ρ = PM/(RT)
比体積v = 1/ρ = RT/(PM)
密度の変化:
- 圧力効果:密度は圧力とともに直線的に増加する
- 温度効果:密度は温度とともに減少する
- 分子量効果:重いガスは密度が高い
- 高度効果:標高が高いほど密度が低くなる
粘度特性
気体粘度は流動抵抗を決定し、工業プロセスにおける熱および物質移動に影響を与える。
粘度特性:
- 温度依存性:温度によって増加する(液体とは異なる)
- プレッシャーの独立性:中等度の圧力では影響は最小限
- 分子の起源:気体層間の運動量移動
- 測定単位:Pa・s、cP(センチポイズ)
粘度の温度関係:
サザランドの公式: μ = μ₀(T/T₀)^(3/2)×(T₀ + S)/(T + S)
Sはサザーランド定数
熱伝導率
気体の熱伝導率は熱伝達能力を決定し、温度と分子特性によって変化する。
熱伝導率の特徴
- 分子メカニズム:分子衝突によるエネルギー移動
- 温度依存性:一般に温度とともに増加する
- プレッシャーの独立性:中程度の圧力で一定
- ガス種依存性:分子量と構造により異なる
気体の圧力、体積、温度はどのように影響し合うのか?
気体における圧力、体積、温度の相互作用は、工業用途におけるすべての気体の挙動を支配する基本的な熱力学的関係に従う。
気体の圧力、体積、温度は、気体の圧力、体積、温度を通して相互に関連している。 理想気体の法則4 PV=nRTであり、どの特性の変化も、特定の熱力学的過程と制約に従って他の特性に影響を与える。
理想気体の法則
理想気体の法則は気体の性質間の基本的な関係を示し、ほとんどの気体計算の基礎となる。
理想気体の法則
PV = nRT (モル体)
PV = mRT/M (マスフォーム)
P = ρRT/M (密度形式)
どこでだ:
- P = 絶対圧
- V = 体積
- n = モル数
- R = 万有引力気体定数 (8.314 J/mol-K)
- T = 絶対温度
- m = 質量
- M = 分子量
- ρ = 密度
コンスタント・プロパティ・プロセス
気体の挙動は、熱力学的過程においてどの特性が一定であるかによって決まる。
プロセスの種類と関係:
| プロセス | 定数プロパティ | 人間関係 | 申し込み |
|---|---|---|---|
| 等温 | 温度 | PV=一定 | ゆっくりとした圧縮/膨張 |
| アイソバリック | 圧力 | V/T = 一定 | 定圧加熱 |
| アイソコリック | ボリューム | P/T = 一定 | 硬質容器での加熱 |
| 断熱 | 熱伝導なし | PV^γ = 一定 | 急速な圧縮/膨張 |
複合ガス法
質量は一定でも複数の性質が変化する場合は、複合気体の法則が適用される。
複合気体の法則の公式:
(p₁v₁)/t₁ = (p₂v₂)/t₂
この関係が不可欠なのだ:
- ガス貯蔵の計算
- パイプライン設計
- プロセス機器のサイジング
- 安全システム設計
実質ガス偏差
現実のガスは特定の条件下で理想的な挙動から逸脱するため、補正係数や代替の状態方程式が必要となる。
逸脱条件:
- 高圧:分子体積が重要になる
- 低温:分子間力が重要になる
- 臨界点付近:相変化効果の発生
- 極性分子:電気的相互作用が行動に影響
圧縮率補正:
PV = ZnRT
ここでZは、実際の気体の挙動を考慮した圧縮性係数である。
私は最近、リヨンのマリー・デュボアというフランス人プロセス・エンジニアのガス貯蔵システムで予期せぬ圧力変動が発生するのを手伝いました。圧縮性係数を使用して実際のガスの挙動を適切に考慮することで、圧力予測精度を95%向上させ、安全上の懸念を解消しました。
産業用途におけるガスの種類とは?
産業用アプリケーションでは様々な種類のガスが使用され、それぞれが固有の特性と挙動を持ち、特定のプロセスやアプリケーションへの適合性を決定する。
工業用ガスには、不活性ガス(窒素、アルゴン)、反応性ガス(酸素、水素)、燃料ガス(天然ガス、プロパン)、特殊ガス(ヘリウム、二酸化炭素)があり、それぞれに特有の取り扱いと安全上の配慮が必要である。
不活性ガス
不活性ガスは化学反応に強く、保護雰囲気や安全用途に最適です。
一般的な不活性ガス:
| ガス | 化学式 | 主要物件 | 工業用 |
|---|---|---|---|
| 窒素 | N₂ | 非反応性、豊富 | ブランケット、パージ、梱包 |
| アルゴン | アー | 緻密で化学的に不活性 | 溶接、金属加工 |
| ヘリウム | 彼は | 軽量、不活性、低沸点 | リークテスト、冷却 |
| ネオン | ネ | 不活性、独特の輝き | 照明、レーザー |
不活性ガス用途:
- 大気保護:酸化と汚染を防ぐ
- 消火活動:酸素を置換して燃焼を防ぐ
- プロセス・ブランケット:不活性環境の維持
- 品質管理:保管中の化学反応を防ぐ
反応性ガス
反応性ガスは化学プロセスに関与し、その化学的活性のために慎重な取り扱いが要求される。
主な反応性ガス
- 酸素(O):燃焼、酸化プロセスをサポート
- 水素(H):燃料ガス、還元剤、高エネルギー密度
- 塩素(Cl):化学処理、水処理
- アンモニア (NH₃):肥料製造、冷凍
安全への配慮:
- 可燃性:多くの反応性ガスは可燃性または爆発性である。
- 毒性:一部のガスは少量の濃度で有害または致死的である。
- 腐食性:化学反応は機器を損傷する可能性がある
- 反応性:他の素材との予期せぬ反応
燃料ガス
燃料ガスは、暖房、発電、工業プロセスにおける燃焼プロセスを通じてエネルギーを供給する。
一般的な燃料ガス:
| 燃料ガス | 発熱量(BTU/フィート³) | 火炎温度 | アプリケーション |
|---|---|---|---|
| 天然ガス | 1000-1100 | 3600 | 暖房、発電 |
| プロパン | 2500 | 3600 | ポータブル暖房、切断 |
| アセチレン | 1500 | 6300 | 溶接、切断 |
| 水素 | 325 | 4000 | クリーン燃料、加工 |
特殊ガス
特殊ガスは、精密な組成と純度レベルを必要とする特定の産業用途に使用される。
特殊ガスのカテゴリー
- 超高純度:半導体製造用>99.999%純度
- 校正用ガス:機器校正用精密混合物
- 医療用ガス:医薬品・ヘルスケア用途
- 研究用ガス:科学的および実験的用途
混合ガス
多くの工業用途では、特定の特性や性能を達成するために混合ガスを使用する。
一般的な混合ガス:
- 空気78% N₂, 21% O₂, 1% その他のガス
- シールドガス:溶接用アルゴン+CO
- 呼吸ガス:ダイビング用酸素+窒素
- 校正ガス:試験用精密混合物
工業用ガスの挙動を支配する気体の法則とは?
気体の法則は、工業システムにおける気体の挙動を予測・制御するための数学的枠組みを提供し、安全で効率的なプロセス設計を可能にします。
ボイルの法則、シャルルの法則、ゲイ=リュサックの法則、アボガドロの法則を含む気体の法則は、理想気体の法則を形成するために組み合わされる。 ドルトンの法則5 とグラハムの法則が気体の混合と輸送特性を支配している。
ボイルの法則の応用
ボイルの法則は、一定の温度における圧力と体積の間の逆相関を説明するもので、圧縮と膨張のプロセスにおいて基本的なものである。
ボイルの法則P₁V₁=P₂V₂(T一定時)
産業用途:
- ガス圧縮:圧縮比と必要パワーの計算
- ストレージシステム:異なる圧力における貯蔵容量の決定
- 空気圧システム:アクチュエータと制御システムの設計
- 真空システム:ポンプの必要量を計算する
圧縮作業の計算:
仕事=P₁V₁ ln(V₁/V₂) (等温プロセス)
シャルルの法則の応用
シャルルの法則は、一定の圧力における体積と温度の関係を支配するもので、熱膨張の計算には欠かせない。
シャルルの法則V₁/T₁=V₂/T₂(P一定時)
産業用途:
- 熱膨張:温度による体積変化を考慮する
- 熱交換器:気体の体積変化を計算する
- 安全システム:熱膨張効果を考慮した設計
- プロセス制御:温度ベースの体積補正
ゲイ=リュサックの法則の応用
ゲイ-リュサックの法則は、一定の体積における圧力と温度の関係であり、圧力容器や安全システムの設計に不可欠である。
ゲイ=リュサックの法則P₁/T₁=P₂/T₂(V一定時)
産業用途:
- 圧力容器設計:温度による圧力上昇の計算
- セーフティ・リリーフ・システム:熱影響を考慮したリリーフバルブのサイズ
- ガス貯蔵:温度による圧力の変化を考慮する
- プロセスの安全性:加熱による過圧を防ぐ
ドルトンの部分圧の法則
ダルトンの法則は気体混合物の挙動を支配しており、複数の気体成分を含むプロセスには不可欠である。
ドルトンの法則P_total = P₁ + P₂ + P₃ + ... + Pₙ
分圧計算:
Pᵢ = (nᵢ/n_total) × P_total = xᵢ × P_total
x_62は成分iのモル分率。
アプリケーション
- ガス分離:分離プロセスの設計
- 燃焼分析:空燃比の計算
- 環境モニタリング:ガス濃度の分析
- 品質管理:ガス純度のモニター
グラハム流出の法則
グラハムの法則は、分子量の違いに基づく気体の拡散と流出速度を説明するものである。
グラハムの法則:r₁/r₂ = √(M₂/M₁)
rは滲出速度、Mは分子量である。
産業用途:
- ガス分離:膜分離システムの設計
- 漏水検知:ガス漏れ率の予測
- ミキシング・プロセス:混合時間の計算
- 物質移動:ガス吸収システムの設計
アボガドロの法則の応用
アボガドロの法則は、温度と圧力が一定であるときの気体の量と体積を関係づける。
アボガドロの法則V₁/n₁ = V₂/n₂ (TとPが一定のとき)
アプリケーション
- 化学量論的計算:化学反応量
- ガスメーター:流量測定
- プロセスデザイン:原子炉のサイジング計算
- 品質管理:濃度測定
私は最近、ミラノのジュゼッペ・ロマノというイタリア人化学エンジニアと仕事をした。彼のガス混合システムは一貫性のない結果を出していた。ダルトンの法則と適切な分圧計算を適用することで、±0.1%の混合精度を達成し、製品の品質問題を解消しました。
結論
ガスは、分子運動、圧縮性挙動、熱力学的法則に支配された圧力-体積-温度の関係によって特徴づけられる物質の基本的な状態を表し、工業用ガスの用途と安全要件を決定する。
ガスの基本概念に関するFAQ
ガスの基本的な定義とは?
気体とは、分子が分子間力を無視して常にランダムに運動している物質の状態で、圧力、体積、温度の関係によって支配される圧縮可能な挙動を示しながら、あらゆる容器を完全に満たしている。
気体分子はどのように動き、どのように振る舞うのか?
気体分子は、衝突が起こるまでは直線上をランダムに動き、速度はマックスウェル・ボルツマン分布に従い、平均運動エネルギーは運動分子理論によれば絶対温度に比例する。
気体は液体や固体と何が違うのか?
気体は、固体や液体の固定された配置とは異なり、分子間の間隔がはるかに大きく、分子間力は無視でき、圧縮性が高く、密度が低く、あらゆる容器を完全に満たすことができる。
理想気体の法則とは何ですか?
理想気体の法則(PV = nRT)は、圧力、体積、温度、気体量を関係付けるもので、工業用途やプロセス設計における気体計算の基本式となる。
気体の圧力、体積、温度は互いにどのように影響し合うのか?
気体の圧力、体積、温度は、熱力学的な関係を通じて相互に関連しており、1つの特性の変化は、特定のプロセス制約(等温、等圧、等温、または断熱)に従って他の特性に影響を与える。
産業ガスの主な種類は?
工業用ガスには、不活性ガス(窒素、アルゴン)、反応性ガス(酸素、水素)、燃料ガス(天然ガス、プロパン)、特殊ガス(ヘリウム、CO₂)があり、それぞれ特有の性質と安全要件がある。
-
分子間力(ファンデルワールス力や水素結合など)について詳しく解説。分子間力とは、隣接する分子間の引力や斥力のことで、物質の物理的性質や状態を決定する。 ↩
-
圧縮性係数(Z)の概念について解説。熱力学において、実際の気体が理想気体の挙動から逸脱することを考慮するために使用される補正係数であり、高圧または低温での正確な計算のために極めて重要である。 ↩
-
気体の運動論とは、気体を構成する分子のランダムな運動や衝突を考慮することで、気体の巨視的な性質(圧力や温度など)を説明する科学モデルである。 ↩
-
理想気体の法則(PV=nRT)とは、圧力、体積、温度、量を関係付けることによって、様々な条件下でのほとんどの気体の挙動を近似する基本的な状態方程式である。 ↩
-
非反応性気体の混合物では、作用する全圧は個々の気体の分圧の和に等しいというダルトンの法則の詳細。 ↩


