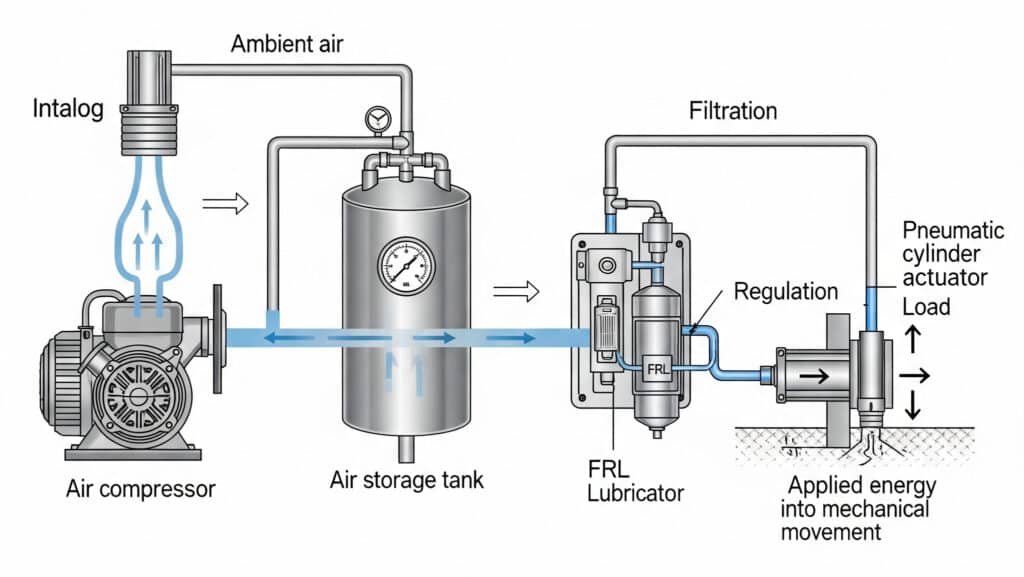
空気圧理論の誤解は、非効率的な設計やシステムの故障によって、メーカーに年間$300億円以上の損害を与えています。エンジニアは空気圧システムを単純化した油圧システムとして扱い、基本的な空気圧の動作原理を無視していることがよくあります。空気圧理論を理解することで、致命的な設計ミスを防ぎ、システム最適化の可能性を引き出すことができます。
空気圧理論は圧縮空気のエネルギー変換に基づいており、大気中の空気は圧縮されて位置エネルギーを蓄え、配電システムを通じて伝送され、アクチュエータを通じて機械的な仕事に変換される。 熱力学原理1 そして流体力学。
半年前、私はスウェーデンのオートメーション・エンジニア、エリック・リンドクヴィスト(Erik Lindqvist)と仕事をした。彼のチームは、空気圧理論の基礎を理解せずに基本的な圧力計算を適用していました。適切な空気圧理論の原理を導入した後、システム性能を60%向上させながら、エネルギー消費を45%削減しました。
目次
- 空気圧理論の基本原理とは?
- 空気圧縮はどのようにして空気圧エネルギーを生み出すのか?
- 空気圧システムを支配する熱力学的原理とは?
- 空気圧機器はどのようにして空気エネルギーを機械的な仕事に変換するのか?
- 空気圧システムにおけるエネルギー伝達メカニズムとは?
- 空気圧理論は産業システム設計にどのように適用されるか?
- 結論
- 空気圧理論に関するFAQ
空気圧理論の基本原理とは?
空気圧理論は、産業用途におけるエネルギー変換、伝達、利用を含む圧縮空気システムを支配する科学原理を包含する。
空気圧理論は、熱力学的エネルギー変換、空気流のための流体力学、力発生のための機械原理、およびシステム自動化のための制御理論に基づいており、統合された圧縮空気動力システムを構築します。
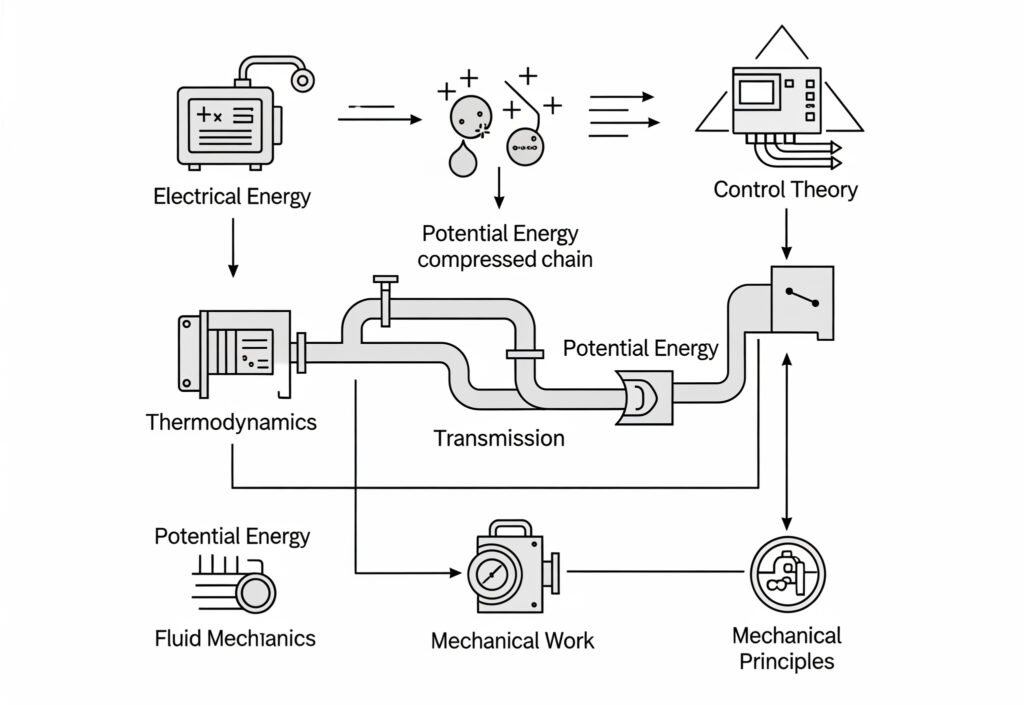
エネルギー変換チェーン
空気圧システムは、電気エネルギーを圧縮空気を通して機械的な仕事に変換する体系的なエネルギー変換プロセスによって作動する。
エネルギー変換シーケンス:
- 電気から機械へ:電気モーターでコンプレッサーを駆動
- 機械式から空圧式へ:コンプレッサーが圧縮空気を作る
- 空気圧ストレージ:レシーバーに貯蔵された圧縮空気
- 空気圧トランスミッション:配管を流通する空気
- 空気圧から機械式へ:空気圧を仕事に変えるアクチュエーター
エネルギー効率分析:
| コンバージョンステージ | 典型的な効率 | エネルギー損失源 |
|---|---|---|
| 電気モーター | 90-95% | 熱、摩擦、磁気損失 |
| エアーコンプレッサー | 80-90% | 熱、摩擦、漏れ |
| 空気分配 | 85-95% | 圧力低下、漏れ |
| 空気圧アクチュエーター | 80-90% | 摩擦、内部漏れ |
| システム全体 | 55-75% | 累積損失 |
エネルギー媒体としての圧縮空気
圧縮空気は空気圧システムにおいてエネルギー伝達媒体として機能し、圧力ポテンシャルによってエネルギーを貯蔵・輸送する。
空気エネルギー貯蔵の原理:
蓄積エネルギー = P × V × ln(P/P₀)
どこでだ:
- P = 圧縮空気圧
- V = 保管容積
- P₀ = 大気圧
エネルギー密度の比較:
- 圧縮空気(100 PSI):0.5BTU/立方フィート
- 作動油 (1000 PSI):0.7BTU/立方フィート
- 電気バッテリー:50-200 BTU/立方フィート
- ガソリン:36,000BTU/ガロン
システム統合理論
空気圧理論には、コンポーネントの相互作用と全体的な性能を最適化するシステム統合の原則が含まれています。
統合の原則:
- 圧力マッチング:適合圧力用に設計されたコンポーネント
- フロー・マッチング:空気供給は消費要件に適合
- レスポンス・マッチング:アプリケーションに最適化されたシステムタイミング
- コントロール・インテグレーション:協調的なシステム運用
基本支配方程式
空気圧理論は、システムの挙動と性能を記述する基本方程式に依存している。
核となる空気方程式:
| 原則 | 方程式 | 申し込み |
|---|---|---|
| 理想気体の法則2 | PV = nRT | 空気挙動予測 |
| フォース・ジェネレーション | F = P × A | アクチュエータ力出力 |
| 流量 | Q = Cd × A × √(2ΔP/ρ) | 気流計算 |
| 仕事の成果 | W = P × ΔV | エネルギー変換 |
| パワー | P = F × v | システム電源要件 |
空気圧縮はどのようにして空気圧エネルギーを生み出すのか?
空気圧縮は、体積を減らし圧力を上げることによって、大気中の空気を高エネルギーの圧縮空気に変換し、空気圧システムのエネルギー源を作り出します。
空気圧縮は、機械的な仕事によって大気を圧縮する熱力学的プロセスを通じて空気エネルギーを作り出し、有用な仕事を行うために解放することができる増加した圧力として位置エネルギーを蓄える。
圧縮熱力学
空気圧縮は、エネルギー要件、温度変化、システム効率を決定する熱力学的原理に従っている。
圧縮プロセスの種類:
| プロセスタイプ | 特徴 | エネルギー方程式 | アプリケーション |
|---|---|---|---|
| 等温3 | 一定温度 | W = P₁V₁ln(P₂/P₁) | 冷却を伴う低速圧縮 |
| 断熱 | 熱伝導なし | W = (P₂V₂-P₁V₁)/(γ-1) | 急速圧縮 |
| ポリトロピック | 実際のプロセス | W = (P₂V₂-P₁V₁)/(n-1) | 実際のコンプレッサー運転 |
どこでだ:
- γ=比熱比(空気の場合は1.4)
- n = ポリトロピック指数(典型的には1.2~1.35)
コンプレッサーの種類と理論
コンプレッサーの種類によって、空気の圧縮を達成するためにさまざまな機械的原理が利用される。
容積式コンプレッサー:
往復動コンプレッサー:
- 理論:ピストン運動が体積変化を生み出す
- 圧縮比:p₂/p₁ = (v₁/v₂)ⁿ
- 効率性70-85% 体積効率
- アプリケーション:高圧、間欠運転
ロータリースクリューコンプレッサー
- 理論:メッシュ状のローターが空気を捕捉・圧縮
- 圧縮:連続プロセス
- 効率性85-95% 体積効率
- アプリケーション:連続使用、中圧
ダイナミック・コンプレッサー:
遠心コンプレッサー:
- 理論:インペラが運動エネルギーを与え、圧力に変換する。
- 圧力上昇: ΔP = ρ(U₂² - U₁²)/2
- 効率性75-85% 総合効率
- アプリケーション:大容量、低圧から中圧
必要な圧縮エネルギー
空気圧縮に必要な理論上のエネルギーと実際のエネルギーは、システムの必要電力と運転コストを決定する。
理論上の圧縮力:
等温電力:P = (mRT/550) × ln(P₂/P₁)
断熱パワー:P=(mRT/550)×(γ/(γ-1))×[(P₂/P₁)^((γ-1)/γ)-1]。
実際の必要電力:
ブレーキ馬力 = 理論出力 / 総合効率
消費電力の例:
| 圧力(PSI) | CFM | 理論HP | 実HP(75% eff) |
|---|---|---|---|
| 100 | 100 | 18.1 | 24.1 |
| 100 | 500 | 90.5 | 120.7 |
| 150 | 100 | 23.8 | 31.7 |
| 200 | 100 | 28.8 | 38.4 |
熱の発生と管理
空気圧縮は大きな熱を発生し、システムの効率と部品の保護のために管理されなければならない。
発熱理論:
発熱量=投入仕事量-有用な圧縮仕事量
断熱圧縮の場合:
温度上昇=T₁[(P₂/P₁)^((γ-1)/γ)-1]である。
冷却方法:
- 空冷:自然または強制空気循環
- 水冷:熱交換器で圧縮熱を除去
- インタークーラー:中間冷却付き多段圧縮
- アフタークーリング:空気貯蔵前の最終冷却
空気圧システムを支配する熱力学的原理とは?
熱力学原理は、空気圧システムにおけるエネルギー変換、熱伝達、および効率を支配し、システムの性能と設計要件を決定する。
空気圧の熱力学には、熱力学の第一法則と第二法則、気体の挙動方程式、熱伝達メカニズム、システムの効率と性能に影響を与えるエントロピーの考慮が含まれる。
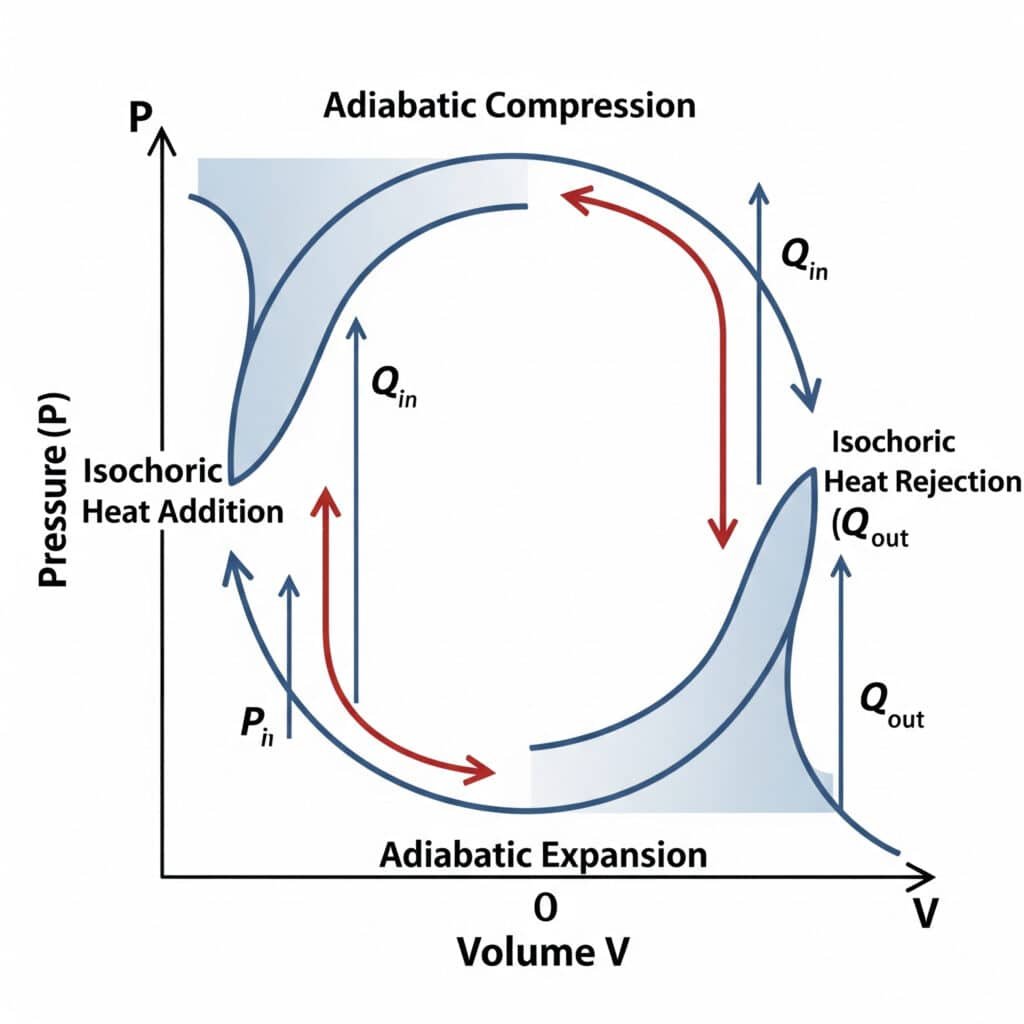
熱力学第一法則の応用
熱力学の第一法則は、空気圧システムにおけるエネルギー保存を支配し、仕事入力、熱伝達、内部エネルギー変化を関連付ける。
第一法則の方程式
ΔU = Q - W
どこでだ:
- ΔU = 内部エネルギーの変化
- Q = システムに加えられる熱
- W = システムが行う仕事
空気圧用途:
- 圧縮プロセス:仕事の投入は内部エネルギーと温度を増加させる
- 拡大プロセス:内部エネルギーは仕事が行われるにつれて減少する
- 熱伝達:システムの効率とパフォーマンスに影響
- エネルギーバランス:総エネルギー投入量は、有用な仕事と損失に等しい
熱力学第二法則の影響
第2の法則は、理論上の最大効率を決定し、システムの性能を低下させる不可逆的なプロセスを特定する。
エントロピーに関する考察:
ΔS≧Q/T (不可逆プロセスの場合)
空気圧システムにおける不可逆プロセス:
- 摩擦損失:機械エネルギーを熱に変換
- スロットル・ロス:仕事量を伴わない圧力降下
- 熱伝達:温度差がエントロピーを生む
- ミキシング・プロセス:異なる圧力流の混合
空気圧システムにおける気体の挙動
実際のガスの挙動は、特定の条件下で理想ガスの仮定から逸脱し、システム性能計算に影響を与える。
理想気体の仮定:
- 体積のない点状分子
- 分子間力がない
- 弾性衝突のみ
- 温度に比例する運動エネルギー
リアルガスコレクション
ファンデルワールス方程式: (P + a/V²)(V - b) = RT
ここで、aとbはガス固有の定数である:
- a:分子間引力
- b:分子体積効果
圧縮率4:
Z = PV/(nRT)
- 理想気体の場合、Z = 1
- 実ガスの挙動はZ≠1
空気圧システムにおける熱伝導
熱伝導は、空気密度、圧力、およびコンポーネントの動作に影響を与える温度変化を通じて、空気圧システムの性能に影響を与えます。
熱伝導モード:
| モード | メカニズム | 空気圧アプリケーション |
|---|---|---|
| 伝導 | 直接接触熱伝達 | 管壁、部品加熱 |
| 対流 | 流体運動熱伝達 | 空冷、熱交換器 |
| 放射線 | 電磁熱伝導 | 高温アプリケーション |
伝熱効果:
- 空気密度の変化:温度は空気の密度と流れに影響する
- コンポーネント拡張:熱膨張がクリアランスに影響
- 水分の結露:冷却により水が発生する可能性がある
- システム効率:熱損失は利用可能なエネルギーを減少させる
空気圧システムの熱力学サイクル
空気圧システムは、効率と性能特性を決定する熱力学的サイクルによって作動する。
基本的な空気圧サイクル:
- 圧縮:システム圧力に圧縮された大気空気
- ストレージ:一定圧力で保存された圧縮空気
- 拡大:空気はアクチュエータを通して膨張し、仕事を行う
- 排気:大気中に放出される膨張した空気
サイクル効率分析:
サイクル効率 = 有用仕事量 / エネルギー投入量
典型的な空気圧サイクル効率:20-40%:
- 圧縮の非効率性
- 圧縮時の熱損失
- 配電における圧力損失
- アクチュエータの膨張損失
- 排気エネルギーが回収されない
私は最近、ノルウェーのラース・アンダーセンという製造エンジニアが、空気圧システムの熱力学を最適化するのを手伝いました。適切な熱回収を実施し、絞り損失を最小限に抑えることで、システム全体の効率を28%から41%に改善し、運転コストを35%削減しました。
空気圧機器はどのようにして空気エネルギーを機械的な仕事に変換するのか?
空気圧コンポーネントは、圧力と流量を力、運動、トルクに変換するさまざまなメカニズムを通じて、圧縮空気のエネルギーを有用な機械的作業に変換します。
空気圧エネルギー変換は、直線的な力には圧力と面積の関係を、運動には圧力と体積の膨張を、回転運動には特殊な機構を利用し、効率は部品の設計と動作条件によって決まる。
リニアアクチュエータ エネルギー変換
リニア 空気圧アクチュエータ ピストン・シリンダー機構により、空気圧を直線的な力と運動に変換する。
力発生理論:
F = P × A - F_摩擦 - F_バネ
どこでだ:
- P = システム圧力
- A = 有効ピストン面積
- F_friction = 摩擦損失
- F_spring = リターンスプリング力(単動式)
仕事量の計算:
仕事=力×距離=P×A×ストローク
出力:
パワー=力×速度=P×A×(ds/dt)
シリンダーの種類と性能
さまざまなシリンダー設計が、特定の用途や性能要件に合わせてエネルギー変換を最適化する。
単動シリンダー:
- エネルギー源:圧縮空気は一方向のみ
- リターン・メカニズム:スプリングまたは重力リターン
- 効率性スプリングロスのため60-75%
- アプリケーション:簡単な位置決め、低荷重のアプリケーション
複動シリンダー:
- エネルギー源:両方向の圧縮空気
- フォース出力:両方向への全圧力
- 効率性適切な設計の75-85%
- アプリケーション:強力で精密なアプリケーション
パフォーマンス比較:
| シリンダータイプ | フォース(伸ばす) | フォース(リトラクト) | 効率性 | コスト |
|---|---|---|---|---|
| 単動 | P × A - F_スプリング | F_スプリングのみ | 60-75% | 低い |
| ダブルアクション | P × A | P × (A - A_rod) | 75-85% | ミディアム |
| ロッドレス | P × A | P × A | 80-90% | 高い |
ロータリーアクチュエータのエネルギー変換
ロータリー空気圧アクチュエータは、様々な機械的配置によって空気圧を回転運動とトルクに変換します。
ベーンタイプロータリアクチュエーター:
トルク=P×A×R×η
どこでだ:
- P = システム圧力
- A = 有効ベーン面積
- R = モーメントアーム半径
- η = 機械効率
ラック&ピニオンアクチュエーター:
トルク=(P×A_ピストン)×R_ピニオン
ここでR_pinionは、直線力を回転トルクに変換するピニオン半径である。
エネルギー変換効率係数
圧縮空気から有用な仕事への空気圧エネルギー変換効率には、複数の要因が影響する。
効率損失源:
| 損失ソース | 典型的な損失 | 緩和戦略 |
|---|---|---|
| シール摩擦 | 5-15% | 低摩擦シール、適切な潤滑 |
| 内部リーク | 2-10% | 高品質のシール、適切なクリアランス |
| 圧力低下 | 5-20% | 適切なサイズ、短い接続 |
| 発熱 | 10-20% | 冷却、効率的な設計 |
| 機械的摩擦 | 5-15% | 高品質のベアリング、アライメント |
総合的な変換効率:
η_total = η_シール × η_漏れ × η_圧力 × η_機械的特性
典型的な範囲:よく設計されたシステムでは60-80%
ダイナミック・パフォーマンス特性
空気圧アクチュエータの性能は、負荷条件、要求速度、システムダイナミクスによって変化します。
力と速度の関係:
圧力と流量が一定の場合:
- 高負荷:低速、高出力
- 低負荷:高速、減速
- コンスタント・パワー:力×速度=一定
応答時間の要因:
- 空気圧縮性:時間遅れを作る
- ボリューム効果:体積が大きいほど反応が鈍くなる
- 流量制限:応答速度の制限
- コントロールバルブのレスポンス:システム・ダイナミクスに影響
空気圧システムにおけるエネルギー伝達メカニズムとは?
空気圧システムにおけるエネルギー伝達には、圧縮空気のエネルギーを供給源から使用地点まで、損失を最小限に抑えながら輸送する複数のメカニズムが関与しています。
空気圧によるエネルギー伝達は、流体力学と熱力学の原理に基づき、配管網による圧力伝達、バルブや継手による流量制御、レシーバーへのエネルギー貯蔵を利用する。
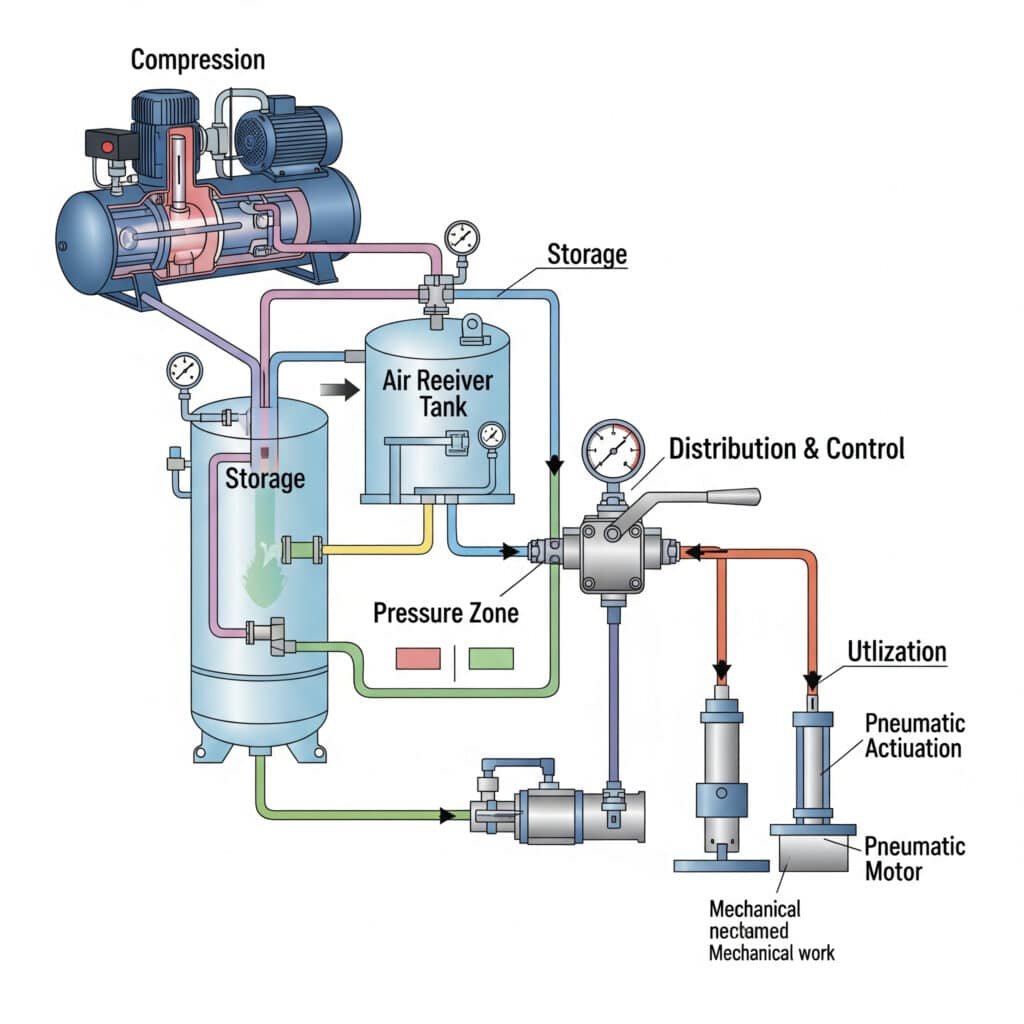
圧力伝達理論
圧縮空気のエネルギーは、空気媒体中を音速で伝播する圧力波によって空気圧システムを通じて伝達される。
圧力波の伝播:
波速=√(γRT)=√(γP/ρ)
どこでだ:
- γ=比熱比(空気の場合は1.4)
- R = 気体定数
- T = 絶対温度
- P = 圧力
- ρ = 空気密度
圧力伝達特性:
- 波のスピード:標準条件下で、空気中約1,100 ft/s
- 圧力均一化:接続されたシステム全体を迅速に
- 距離効果:一般的な空気圧システムには最小
- 周波数特性:高周波の圧力変化を減衰
フローベースのエネルギー移動
空気圧システムによるエネルギー伝達は、アクチュエータや部品に圧縮空気を送る空気流量に依存します。
マスフロー・エネルギー伝達:
エネルギー流量 = ṁ × h
どこでだ:
- ↪Ll_1 = 質量流量
- h = 圧縮空気の比エンタルピー
容積流量の考慮:
Q_actual = Q_standard × (P_standard/P_actual) × (T_actual/T_standard)
フロー・エネルギーの関係:
- ハイフロー:迅速なエネルギー供給、素早い反応
- ローフロー:エネルギー供給が遅い、反応が遅れる
- 流量制限:エネルギー伝達効率の低下
- フロー制御:エネルギー供給量を調整
配電系統のエネルギー損失
空気圧分配システムは、システムの効率と性能を低下させるエネルギー損失を経験する。
主な損失源
| 損失タイプ | 原因 | 典型的な損失 | 緩和 |
|---|---|---|---|
| 摩擦損失 | パイプ壁の摩擦 | 2-10 PSI | 適切なパイプサイジング |
| フィッティング損失 | 流れの乱れ | 1-5 PSI | 継手の最小化 |
| 漏れ損失 | システム・リーク | 10-40% | 定期メンテナンス |
| 圧力低下 | 流量制限 | 5-15 PSI | 制限の撤廃 |
圧力損失の計算:
ΔP = f × (L/D) × (ρV²/2)
どこでだ:
- f = 摩擦係数
- L = パイプの長さ
- D = パイプの直径
- ρ = 空気密度
- V = 空気速度
エネルギー貯蔵と回収
空気圧システムは、効率と性能を向上させるために、エネルギー貯蔵・回収機構を利用している。
圧縮空気の貯蔵:
蓄積エネルギー = P × V × ln(P/P₀)
ストレージの利点:
- ピーク需要:一時的な高需要への対応
- 圧力安定性:圧力を一定に保つ
- エネルギー・バッファ:需要変動の平準化
- システム保護:圧力変動を防ぐ
エネルギー回収の機会:
- 排気の回収:膨張エネルギーの獲得
- 熱回収:圧縮熱を利用する
- 圧力回復:部分的に膨張した空気を再利用
- 再生システム:多段階エネルギー回収
制御システム エネルギー管理
空気圧制御システムは、消費量を最小限に抑えながら性能を最適化するために、エネルギー伝達を管理します。
コントロール戦略:
- 圧力調整:最適な圧力レベルを維持
- フロー制御:需要と供給を一致させる
- シーケンス制御:複数のアクチュエーターを調整
- エネルギー監視:消費量の追跡と最適化
高度な制御技術:
- 可変圧力:負荷要件に合わせて圧力を調整
- 需要に基づくコントロール:必要なときだけ空気を供給する
- ロード・センシング:実際の需要に基づいてシステムを調整する
- 予測制御:エネルギー需要の予測
空気圧理論は産業システム設計にどのように適用されるか?
空気圧理論は、エネルギー消費と運用コストを最小限に抑えながら、性能要件を満たす効率的で信頼性の高い産業用空気圧システムを設計するための科学的基礎を提供します。
産業用空気圧システム設計は、熱力学原理、流体力学、制御理論、機械工学を応用し、製造、オートメーション、プロセス制御の用途に最適化された圧縮空気システムを構築します。
システム設計手法
空気圧システムの設計は、理論的な原理を実際の要件に適用する体系的な方法論に従います。
設計プロセスのステップ:
- 要求分析:パフォーマンス仕様の定義
- 理論計算:空気圧の原理を応用
- コンポーネントの選択:最適なコンポーネントの選択
- システム・インテグレーション:コーディネート・コンポーネントの相互作用
- パフォーマンスの最適化:エネルギー消費の最小化
- 安全性分析:安全運転の確保
設計基準に関する考慮事項:
| 設計係数 | 理論的根拠 | 実践的応用 |
|---|---|---|
| 戦力要件 | F = P × A | アクチュエータのサイジング |
| 速度要件 | 流量計算 | バルブとパイプのサイジング |
| エネルギー効率 | 熱力学的分析 | コンポーネントの最適化 |
| 応答時間 | 動的解析 | 制御システム設計 |
| 信頼性 | 故障モード解析 | コンポーネントの選択 |
圧力レベルの最適化
最適なシステム圧力は、性能要件とエネルギー効率および部品コストのバランスをとります。
圧力選択理論:
最適圧力=f(必要力量、エネルギーコスト、部品コスト)
圧力レベル分析:
- 低圧 (50-80 PSI):より低いエネルギーコスト、より大きな部品
- 中圧(80~120 PSI):性能と効率のバランス
- 高圧 (120-200 PSI):コンパクトな部品、高いエネルギーコスト
圧力がエネルギーに与える影響:
パワー ∝ P^0.286 (等温圧縮の場合)
20%の圧力上昇=5.4%の出力上昇
コンポーネントのサイズと選択
理論的な計算により、システムの性能と効率に最適な部品サイズを決定する。
アクチュエータのサイジング:
必要圧力=(負荷力+安全係数)/有効面積
バルブのサイジング:
Cv = Q × √(ρ/ΔP)
どこでだ:
- Cv = バルブ流量係数
- Q = 流量
- ρ = 空気密度
- ΔP = 圧力降下
パイプのサイズ最適化:
経済直径=K×(Q/v)^0.4
Kはエネルギーコストとパイプコストに依存する。
システム統合理論
空気圧システム統合は、制御理論とシステムダイナミクスを応用してコンポーネントの動作を調整する。
統合の原則:
- 圧力マッチング:コンポーネントは互換性のある圧力で動作
- フロー・マッチング:需要に見合った供給能力
- レスポンス・マッチング:システムタイミングの最適化
- コントロール・インテグレーション:協調的なシステム運用
システム・ダイナミクス:
どこでだ:
- K = システム・ゲイン
- τ = 時定数
- s = ラプラス変数
エネルギー効率の最適化
理論的分析により、空気圧システムのエネルギー効率改善の機会を特定。
効率最適化戦略:
| 戦略 | 理論的根拠 | 節約の可能性 |
|---|---|---|
| 圧力の最適化 | 熱力学的分析 | 10-30% |
| リーク除去 | 質量保存 | 20-40% |
| コンポーネントのライトサイジング | フローの最適化 | 5-15% |
| 熱回収 | 省エネルギー | 10-20% |
| 制御の最適化 | システム・ダイナミクス | 5-25% |
ライフサイクルコスト分析:
総費用=イニシャルコスト+ランニングコスト×現在価値係数
運転コストには、システム寿命期間中のエネルギー消費が含まれる。
私は最近、空気圧システムの再設計プロジェクトで理論的検証を必要としていたオーストラリアの製造エンジニア、マイケル・オブライエンと仕事をした。適切な空気圧理論の原則を適用することで、システム設計を最適化し、性能を35%向上させ、メンテナンスコストを40%削減しながら、52%のエネルギー削減を達成しました。
安全理論の応用
空気圧安全理論により、性能と効率を維持しながらシステムを安全に作動させることができます。
安全分析法:
- ハザード分析:潜在的な安全リスクの特定
- リスク評価:確率と結果を定量化する
- 安全システム設計:保護措置の実施
- 故障モード解析:部品の故障予測
安全設計の原則:
- フェイルセーフ設計:システムが安全な状態に移行しない
- 冗長性:複数の保護システム
- エネルギー・アイソレーション:蓄積エネルギーを除去する能力
- 圧力リリーフ:過圧状態を防ぐ
結論
空気圧理論は、圧縮空気システムを支配する熱力学的エネルギー変換、流体力学、および制御原理を網羅し、効率的で信頼性の高い産業オートメーションおよび製造システムを設計するための科学的基礎を提供します。
空気圧理論に関するFAQ
空気圧システムの基礎理論とは?
空気圧理論は圧縮空気のエネルギー変換に基づいており、大気中の空気を圧縮して位置エネルギーを蓄え、配電システムを通じて伝送し、熱力学と流体力学の原理を利用してアクチュエーターを通じて機械的な仕事に変換する。
熱力学は空気圧システムにどのように適用されるのか?
熱力学は、第一法則(エネルギー保存)と第二法則(エントロピー/効率限界)を通じて空気圧システムにおけるエネルギー変換を支配し、圧縮仕事、発熱、最大理論効率を決定する。
空気圧における主要なエネルギー変換メカニズムとは?
空気圧エネルギー変換には、電気から機械(コンプレッサー駆動)、機械から空気圧(空気圧縮)、空気圧貯蔵(圧縮空気)、空気圧伝送(分配)、空気圧から機械(アクチュエーター作業出力)が含まれる。
空気圧機器はどのようにして空気エネルギーを仕事に変えるのか?
空気圧コンポーネントは、直線的な力には圧力と面積の関係(F = P × A)を、運動には圧力と体積の膨張を、回転運動には特殊なメカニズムを用いて空気エネルギーを変換し、効率は設計と動作条件によって決まる。
空気圧システムの効率に影響を与える要因は何ですか?
システム効率は、圧縮損失(10-20%)、分配損失(5-20%)、アクチュエーター損失(10-20%)、発熱(10-20%)、および制御損失(5-15%)の影響を受け、その結果、典型的な総合効率は20-40%となる。
空気圧理論は産業システムの設計をどのように導くのか?
空気圧理論は、熱力学的計算、流体力学的分析、コンポーネントのサイジング、圧力の最適化、およびエネルギー効率の分析を通じて、最適な産業用圧縮空気システムを構築するためのシステム設計の科学的基礎を提供します。
-
物理システムにおけるエネルギー、熱、仕事、エントロピーを支配する第0法則、第1法則、第2法則、第3法則を含む熱力学の基本原理を概説する。 ↩
-
理想気体の法則(PV=nRT)を詳しく解説。理想気体の法則は、様々な条件下におけるほとんどの気体の挙動を近似し、圧力、体積、温度、気体量を関係づける基本的な状態方程式である。 ↩
-
等温(一定温度)、断熱(熱伝導なし)、多熱(熱伝導あり)の主要な熱力学的過程を説明し、比較する。 ↩
-
圧縮性係数(Z)の概念を説明。理想気体の挙動からの実際の気体の乖離を表す補正係数で、理想気体の法則をより正確に実計算で修正するために使用される。 ↩
-
制御理論において、線形時不変システムの入力と出力の関係をラプラス領域でモデル化する数学的表現である伝達関数の定義を提供する。 ↩


