
空気圧シリンダの速度が一定しない、またはストローク終了時に予期せぬ衝撃が発生するなどの問題に悩まされていませんか?このような一般的な問題は、ピストン運動学に対する理解不足に起因することがよくあります。多くのエンジニアは、システム性能を決定する重要な運動パラメータを見落とし、力要件のみに注目しています。
ピストン運動学1 は、圧力と速度の関係、加速度限界、および緩衝要件を通じて、空気圧システムの性能に直接影響を与えます。これらの原理を理解することで、エンジニアはコンポーネントの適切なサイズ設定、実際の動作プロファイルの予測、ロッドレスシリンダやその他の空気圧アクチュエータの早期故障の防止が可能になります。
Beptoで15年以上空気圧システムに携わってきましたが、これらの基本原理を理解することで、お客様が持続的な性能問題を解決し、機器の寿命を3~5倍延ばすことができた事例を数え切れないほど見てきました。
目次
- 等速運動に必要な圧力とは?
- 空気圧シリンダーの最大加速度はどのように計算しますか?
- クッションタイムはなぜ重要で、どのように計算されるのか?
- 結論
- 空気圧システムにおけるピストン・キネマティクスに関するFAQ
等速運動に必要な圧力とは?
多くのエンジニアは、利用可能な最大圧力を空気圧システムに適用するだけですが、このアプローチは非効率的で、ぎくしゃくした動き、過度の摩耗、エネルギーの浪費につながります。
ここで、P は圧力、F は外的負荷力、Fr は摩擦抵抗、A はピストン面積です。この計算により、エネルギーを浪費し、部品の摩耗を早める過剰な圧力をかけることなく、スムーズで効率的な動作が保証されます。
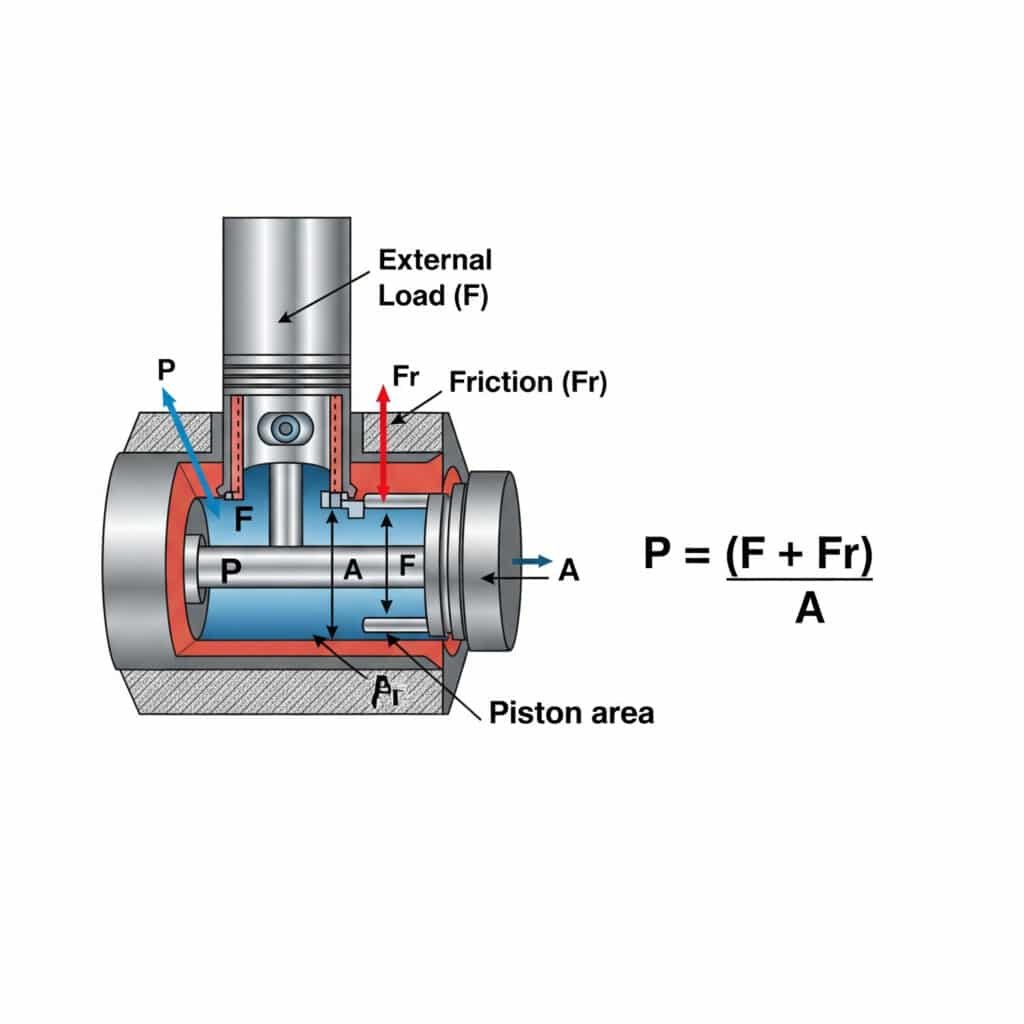
等速運動に必要な圧力を理解することは、システムの設計と運転に実用的な意味を持つ。これを実用的な洞察に分解してみよう。
定速走行に必要な圧力に影響する要因
等速を維持するために必要な圧力は、いくつかの要因に左右される:
| ファクター | 圧力要件への影響 | 実践的考察 |
|---|---|---|
| 外部負荷 | 直接的な直線関係 | 方向性や外力によって異なる |
| 摩擦 | 必要な圧力を加える | シールの摩耗と潤滑による変化 |
| ピストン面積 | 反比例 | 口径が大きい=必要圧力が低い |
| 給気制限 | ライン/バルブの圧力低下 | 圧力損失を最小限に抑える部品サイズ |
| 背圧 | 動議に反対 | 排気流量を考慮する |
安定した動きのための最低圧力の計算
安定した動きに必要な最低圧力を決定する:
- 外部荷重に打ち勝つために必要な力を計算する。
- 摩擦力(通常、最大力の3~20%)を加える。
- 有効ピストン面積で割る
- 安定係数(通常10-30%)を加える。
例えば、内径40mmのロッドレスシリンダーで、荷重10kg、摩擦15%の場合:
| パラメータ | 計算 | 結果 |
|---|---|---|
| 負荷力 | 10kg×9.81m/s²の場合 | 98.1N |
| 摩擦力 | 6barで15%の最大力 | ~45N |
| 総力戦 | 98.1N + 45N | 143.1N |
| ピストン面積 | π×(0.02m)²(平方メートル | 0.00126m² |
| 最低圧力 | 143.1N÷0.00126平方メートル | 113,571Pa(1.14バール) |
| 20%使用時 安定係数 | 1.14バール×1.2 | 1.37バール |
実世界での応用圧力最適化によるエネルギー節約
昨年、私はミシガン州にある家具製造工場の生産エンジニア、ロバートと仕事をした。彼の自動組立ラインでは、負荷に関係なく6バールの供給圧力でフル稼働するロッドレスシリンダーを使用していた。
彼のアプリケーションを分析した結果、ほとんどの動作は安定した動作のために2.5~3バールしか必要ないと判断した。そのため 比例圧力調整器その結果、同じサイクル時間を維持しながら、エア消費量を40%削減することができました。これにより、年間約$12,000のエネルギーコストを削減するとともに、シールの摩耗を減らし、メンテナンス間隔を延長することができました。
実システムにおける速度と圧力の関係
実際には、圧力と速度の関係は、以下の理由により完全な直線ではない:
- 流量制限:バルブとポートのサイジングは最高到達速度に影響する
- 圧縮効果:空気は圧縮されやすく、加速の遅れを引き起こす
- スティック・スリップ現象:摩擦特性は速度によって変化する
- 慣性効果:質量の加速にはさらなる力/圧力が必要
空気圧シリンダーの最大加速度はどのように計算しますか?
加速度限界を理解することは、空気圧システムにおける過度の衝撃や振動、部品の早期故障を防ぐために非常に重要です。
ここで、a は加速度、P は圧力、A はピストン面積、F は外部荷重、Fr は摩擦抵抗、m は移動質量です。この式は、空気圧アクチュエータがどの程度の速さで動作を開始または停止できるかの物理的限界を定義しています。
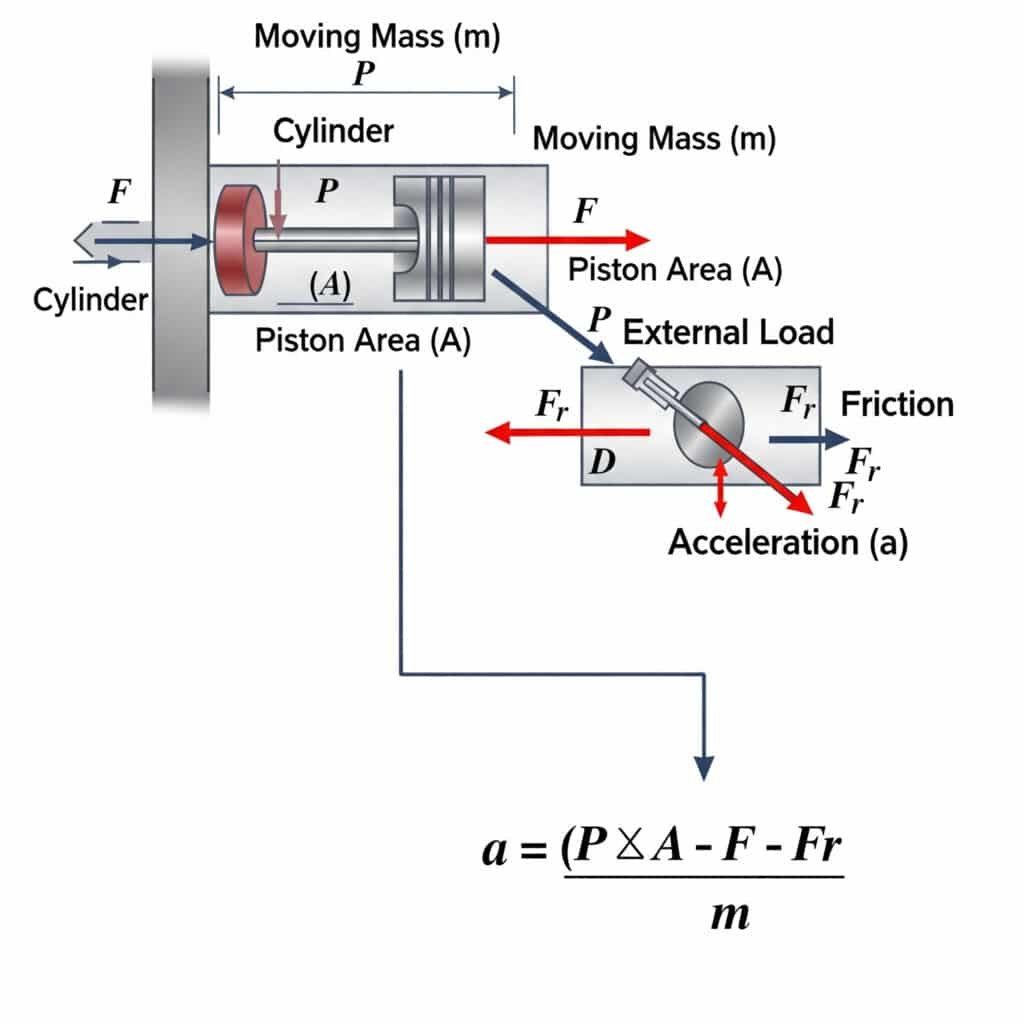
理論的な加速限界は、システム設計やコンポーネントの選択において、実用上重要な意味を持つ。
加速限界方程式の導出
加速度限界の式は次のようになる。 ニュートンの第二法則2 (F=ma):
- 加速に利用できる正味の力は次のとおりである:Fnet = Fpressure - Fload - Ffriction
- 圧力=P×A
- 従って:a = Fnet/m = (P × A - F - Fr)/m
シリンダータイプ別の実用加速度限界
シリンダー設計が異なれば、実用的な加速限界も異なる:
| シリンダータイプ | 典型的な最大加速度 | 制限要因 |
|---|---|---|
| 標準ロッドシリンダー | 10-15 m/s² | ロッド座屈、ベアリング荷重 |
| ロッドレスシリンダー(マグネット式) | 8~12 m/s² | 磁気結合強度 |
| ロッドレスシリンダー(機械式) | 15-25 m/s² | シール/ベアリング設計、内部摩擦 |
| ガイドシリンダー | 20-30 m/s² | ガイドシステム剛性、ベアリング容量 |
| 衝撃シリンダー | 50~100m/s²以上 | 高加速専用設計 |
加速度計算における質量の考慮
加速度を計算する場合、すべての移動質量を含めることが重要である:
- ピストンアセンブリ:ピストン、シール、コネクティングエレメントを含む
- 負荷質量:移動する外部負荷
- 移動する空気の有効質量:多くの場合無視できるが、高速アプリケーションでは重要
- 取り付け部品による質量の増加:ブラケット、センサーなど
ロッドレスシリンダーシステムに謎の故障が発生したフランスの顧客を助けたことがある。シリンダーは15kgの負荷に対して正しいサイズだったが、数千回のサイクルで常に故障していた。
調査の結果、取り付けプレートとアタッチメントの質量12kgを計算に入れていなかったことがわかりました。実際の可動質量は計算の2倍近くあり、シリンダーの設計限界を超える加速力が発生した。より大きなシリンダーにアップグレードしたところ、故障は完全に止まった。
加速制御方法
安全な範囲内で加速をコントロールすること:
- 流量制御バルブ:初動時の流量を制限
- 比例弁:制御された圧力上昇を提供
- 多段加速:段階的な圧力上昇を使用
- 機械的減衰:外部ショックアブソーバーの追加
- 電子制御:用途 空圧サーボシステム3 加速度フィードバック付き
クッションタイムはなぜ重要で、どのように計算されるのか?
適切なストローク終了時のクッションは、衝撃による損傷を防ぎ、騒音を低減し、空気圧シリンダの寿命を延ばすために不可欠です。クッション時間を理解することは、エンジニアがサイクルタイムとコンポーネントの寿命のバランスをとるシステムを設計するのに役立ちます。
ここで、tは時間、sはクッションストローク長、aは減速度である。この時間は、シリンダーと付属部品の損傷を防ぐために重要な、衝突前に移動質量を安全に減速させるのにかかる時間を表します。

ここでは、クッション時間の計算の実際的な側面と、システム設計へのその影響を探ってみよう。
空気圧クッションの背後にある物理学
空気クッション 制御された空気圧縮と制限された排気によって機能する:
- ピストンがクッション室に入ると、排気経路が制限される。
- 閉じ込められた空気が圧縮され、背圧が高まる
- この背圧は、ピストンを減速させる反力を生み出す。
- 減速プロファイルはクッションの設計と調整によって決まる
最適な緩衝時間の計算
最適なクッション時間は、衝撃防止とサイクルタイム効率のバランスをとる:
| パラメータ | フォーミュラ | 例 |
|---|---|---|
| クッション距離 | シリンダー設計に基づく | 15mm(40mm口径の代表値) |
| 必要な減速度 | a = v²/(2s) | v=0.5m/s、s=15mmの場合:a=8.33m/s²。 |
| 緩衝時間 | t = √(2s/a) | t = √(2×0.015/8.33) = 0.06s |
| 圧力上昇 | P = P₀(V₀/V)^γ | クッション・チャンバーの形状による |
クッション性能に影響する要因
実際のクッション性能にはいくつかの要因が影響する:
- クッション・シール・デザイン:クッション時の空気漏れに影響
- ニードルバルブ調整:排気制限率をコントロール
- 移動質量:荷重が重くなるとクッション時間が長くなる
- アプローチ速度:高速になるとクッション距離が長くなる
- 動作圧力:最大対抗力に影響
クッションの種類と用途
用途によって適切なクッション機構は異なる:
| クッションタイプ | 特徴 | ベストアプリケーション |
|---|---|---|
| 固定クッション | シンプル、無調整 | 軽負荷、安定した動作 |
| 調整可能なクッション | ニードルバルブで調整可能 | さまざまな負荷、柔軟なアプリケーション |
| 自動調整クッション | さまざまな条件に適応 | スピードと負荷の変化 |
| 外部ショックアブソーバー | 高いエネルギー吸収 | 高荷重、高速 |
| 電子クッション | 正確に制御された減速 | サーボ空気圧システム |
ケーススタディハイサイクル用途におけるクッションの最適化
私は最近、ドイツの自動車部品メーカーの設計エンジニア、トーマスと仕事をした。彼の組立ラインでは、毎分45サイクルで作動するロッドレスシリンダーを使用していましたが、シールの不具合や取り付けブラケットの破損が頻発していました。
解析の結果、移動質量に対してクッション時間が短すぎ、ストロークの両端で3G近い衝撃力が発生していることが判明した。クッションストロークを12mmから20mmに増やし、ニードルバルブの設定を最適化することで、クッション時間を0.04秒から0.07秒に延長した。
この一見小さな変更により、衝撃力は60%以上減少し、ブラケットの損傷は完全になくなり、シール寿命は3ヶ月から1年以上に延びた。
実用的なクッション調整の手順
ロッドレスシリンダーに最適なクッション性能を発揮:
- クッションバルブを全開にしてスタート(最小限の制限)
- スムーズな減速が得られるまで、クッションバルブを徐々に閉じる。
- 予想される最小負荷と最大負荷によるテスト
- 全速度域でのクッション性能を検証
- クッション不足を示す衝撃音を聞く
- 実際の減速時間を測定して計算を確認する
結論
効率的で信頼性の高い空圧システムを設計するには、一定速度の圧力要件から加速限界、クッション時間の計算に至るまで、ピストン運動の原理を理解することが不可欠です。これらの原理をロッドレスシリンダのアプリケーションに適用することで、性能を最適化し、エネルギー消費を削減し、部品の寿命を大幅に延ばすことができます。
空気圧システムにおけるピストン・キネマティクスに関するFAQ
特定のシリンダー回転数に必要な圧力は?
必要な圧力は、荷重、摩擦、シリンダー面積に依存する。P=(F+Fr)/Aで計算します。ここで、Fは外力、Frは摩擦抵抗、Aはピストン面積です。一般的なロッドレスシリンダーで10kgの荷重を水平に移動させる場合、中程度の速度で安定した運動を行うには約1.5~2バールが必要です。
空気圧シリンダーはどのくらいの速度で加速できますか?
空気圧シリンダの最大加速度は、a = (P × A - F - Fr)/m で計算されます。一般的なロッドレスシリンダは、設計にもよりますが、10~25 m/s²の加速度を達成できます。これは、最適な条件下では、およそ20~50ミリ秒で0.5 m/sの速度に達することになります。
ロッドレスシリンダーの最高速度を制限する要因は何ですか?
最高速度は、バルブの流量、給気量、ポートのサイジング、緩衝能力、シール設計によって制限されます。ほとんどの標準的なロッドレスシリンダーは0.8-1.5m/sの最高速度のために設計されているが、特別な高速設計は2-3m/sに達することができる。
自分の用途に適したクッションを計算するには?
移動する荷物の運動エネルギー(KE = ½mv²)を決定し、クッション・システムがこのエネルギーを吸収できることを確認することによって、適切なクッションを計算する。クッション時間は、t = √(2s/a)を用いて計算する。ここで、sはクッション距離、aは望ましい減速率である。
空気圧シリンダーの加速が速すぎるとどうなりますか?
過度の加速は、取り付け部品への機械的ストレス、シールの早期摩耗、振動や騒音の増加、負荷の移動や損傷の可能性、システム精度の低下を引き起こす可能性があります。また、精密な用途では、製品の品質に影響を与えるギクシャクした動きにつながることもあります。
荷重の方向は、移動に必要な圧力にどのように影響しますか?
荷重の向きは圧力要件に大きく影響します。重力に逆らって動く垂直荷重は、重力に打ち勝つための追加圧力を必要とします(P = F/A + Fg/A + Fr/A)。水平荷重は、摩擦と慣性に打ち勝つだけでよい。傾斜荷重は、角度の正弦に基づいてこれらの両極端の間に位置します。



